基于FCM 聚类和卷积神经网络的跌倒识别算法

朱 艳，李曙生，谢忠志

（泰州职业技术学院机电技术学院，泰州 225300）

引 言

随着人类社会的不断发展以及医疗条件的快速进步，人类平均寿命日益增加，老年人口所占的比例越来越大。随着年龄的增大，人体机能不断下降，从而造成跌倒的几率越来越大，跌倒成为危害老年人身体健康的主要外因［1⁃2］，成为老年人死亡的头号杀手。调查和研究发现，在跌倒事件发生后，如果能在第一时间得到合理的医疗救助，那么跌倒造成的伤害程度就可以降到最低，从而大大降低死亡风险，提高救治率。中国60 岁以上老年人口的数量不断增加，是世界上唯一老年人口超过两亿的国家［3］。因此，如何及时准确地对老年人进行跌倒检测，并在第一时间发出求救信号对保障老年人的生命健康尤为关键。

目前，国内外跌倒检测研究主要有3 种方法。第1 种为基于环境参数的跌倒检测［4⁃8］，Litvak 等［4］在房间地板上安装了多个声音和压力传感器，通过分析采集到的声频和压力信号来识别跌倒行为。Al⁃wan 等［6］在地板表面安装了压电式振动传感器，通过监测人体正常行走和跌倒时采集到的振动信号差别来识别跌倒行为。该方法成本较高，受周围环境影响较大，识别精度较低。第2 种为基于穿戴式智能传感器的跌倒检测［9⁃13］。Jahanjoo 等［10］从加速度传感器获取的三维加速度信息中提取跌倒特征序列，并采用模糊神经网络模型对样本进行分类，得到较好的识别效果。Kumar 等［11］将加速度传感器和陀螺仪穿戴于人身，并将获取的加速度和角度数据，通过支持向量机（Support vector machine，SVM）分类器进行跌倒识别，获取了93% 的识别精度。该方法虽然识别精度高，但穿戴物影响人体舒适度，因此应用局限性较大。第3 种为基于视觉传感器的检测方法，按照采用的视觉传感器种类不同，可分为基于红绿蓝（Red green blue，RGB）视觉传感器的跌倒检测［14⁃16］和基于深度视觉传感器的跌倒检测［17⁃18］。Miguel 等［16］将RGB 摄像头获取的二维图像通过帧差法和光流法提取特征信息，采用K 邻近（K⁃nearest neighbor，KNN）分类器进行跌倒识别，获得了96% 的识别精度。但该方法只能得到二维图像信息，特征提取困难且易造成用户个人隐私泄露。王君泽等［18］以深度视觉传感器获取骨架数据，实时计算骨架点的空间坐标位置进行跌倒识别。该方法不涉及个人隐私，同时特征提取容易，识别精度较高，成为近年来跌倒检测的主要研究方向之一。

本文以Kinect V2 深度视觉传感器为监测手段，以获取的骨架节点为数据分析源，基于模糊C 均值（Fuzzy C⁃means，FCM）聚类算法和卷积神经网络（Convolutional neural networks，CNN）算法建立跌倒识别模型对人体跌倒行为进行监控。

1 跌倒检测系统结构

系统结构主要由硬件部分和软件部分组成，如图1 所示。硬件部分主要由Kinect V2、计算机、USB 通信电缆几部分组成，深度视觉传感器Kinect V2 用于实时采集人体3D 深度图像。计算机上安装的软件平台对采集到的图像数据进行处理。Kinect V2 通过USB通信电缆将数据传输给计算机。 软件部分由Kinect Developer Toolkit、LabVIEW 和MATLAB 组成。Ki⁃nect Developer Toolkit 作为传感器开发工具包，可以将采集到的3D 深度图像，转换到骨架追踪系统，然后采用LabVIEW 和MATLAB 混合编程的方式完成跌倒识别算法设计。由LabVIEW 中提供的Script 节点，实现两软件之间的数据传输。

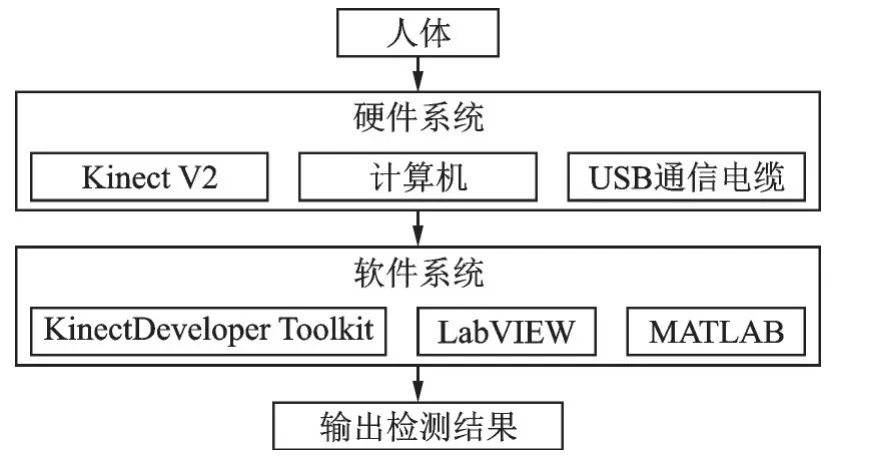
图1 系统结构Fig.1 System structure

2 改进型FCM 骨架节点聚类中心计算

2.1 骨骼节点数据获取

使用Kinect SDK 和Kinect dirver 配合LabVIEW 平台，完成对Kinect V2 的开发，LabVIEW 通过调用外部DLL 文件的方式完成骨架节点数据的获取，人体骨骼节点分布如图2 所示。由图2 可知，人体骨架由1 号节点人体中心为分界点，可分为上身节点和下身节点两部分。

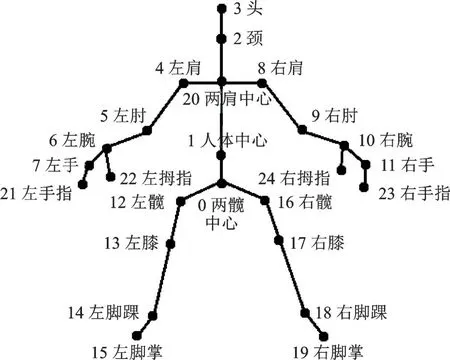
图2 人体25 个骨骼关节点分布图Fig.2 Distribution of 25 joints in human body

2.2 改进型FCM 聚类中心算法设计

跌倒时，人体会在极短的时间内由直立状态转换到躺卧状态，各骨架节点的高度、速度、加速度、节点间角度等参数都会发生较大变化，各节点会表现出一定的跌倒识别性，并且各节点之间具有明显的关联性。若将所有骨骼节点均作为跌倒识别的数据源，会造成样本数据维度增加，识别速度较慢。而若仅选择几个关键骨骼点作为分析数据源，又会造成跌倒特征提取不充分，识别准确率不高。为有效解决上述矛盾，本文采用FCM 聚类算法对除1号节点（人体中心）之外的24 个骨骼点进行分类，选取聚类中心的个数k= 2，得到上身聚类中心O1(xu，yu，zu)和下身聚类中心O2(xd，yd，zd)，以2 个聚类中心和1 号节点Oc(x1，y1，z1)3 个点作为数据分析源，提取跌倒识别特征数据。

假设样本集X，如果想把这些数据划分成k个类，每个类有一个中心，那么就应该有k个聚类中心Oi，每个样本j属于第i类的隶属度为μij，定义一FCM 目标函数如式（1）所示，其约束条件如式（2）所示。FCM 算法就是目标函数最小化的求解过程，通过拉格朗日乘数法求解J在隶属度函数约束下的优化，可得到隶属度μij计算公式（3），聚类中心k i计算公式（4）

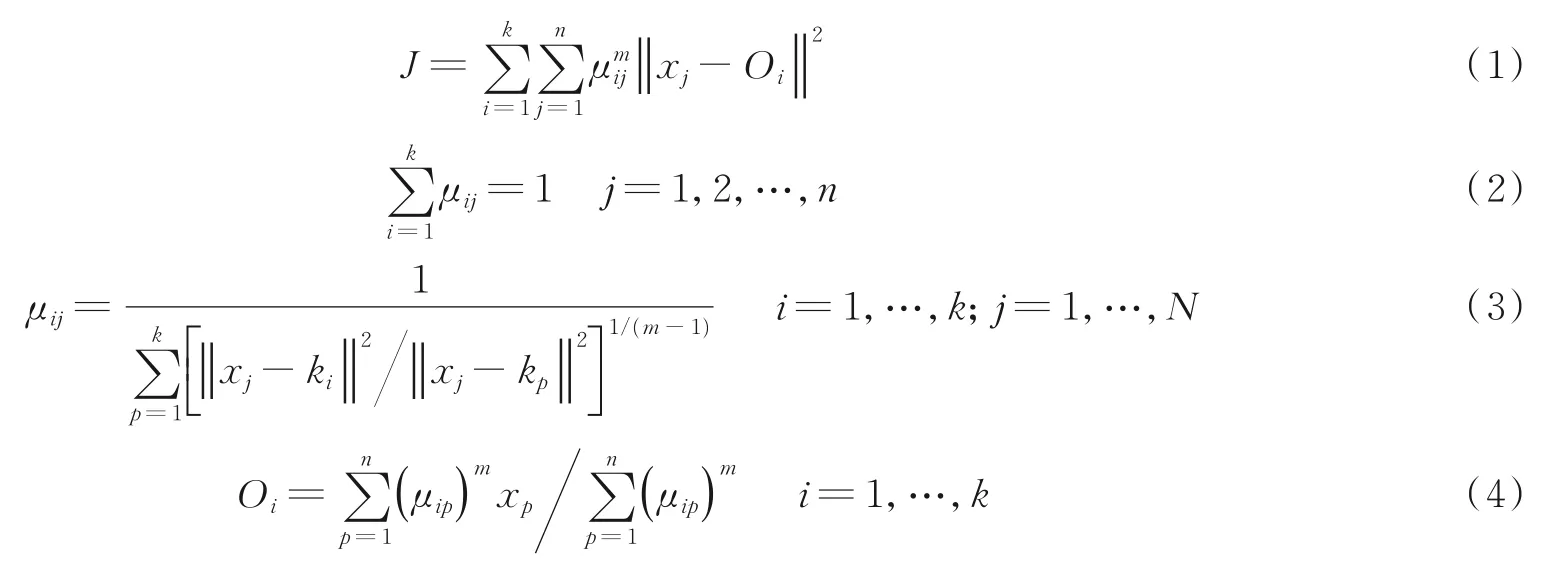
式中：Oi表示聚类中心；m∈(1，∞)为模糊指数，用来控制模糊程度，值越大，分类的模糊程度越高，本文选取表示样本数据xj与k i之间的欧式距离。

传统FCM 聚类算法在初始化聚类中心时，一般采用从聚类数据中随机选取的方式确定，可能会导致算法在迭代过程中收敛速度非常缓慢，甚至会出现收敛到局部极小的情况，无法得到全局最优解。因此，本文对传统FCM 算法进行改进，提出一种新的初始聚类中心的选择方法，解决了传统算法的缺点，改进FCM 算法流程为：

步骤1计算24 个骨骼节点任意两点之间的欧式距离，将距离最小的两个节点定义为一类，并选取这两个节点的中点作为第1 个初始聚类中心点O1；

步骤2分别计算O1和剩余22 个节点之间的欧式距离，找到和O1之间距离最大的骨架节点xj；

步骤3分别计算xj和剩余21 个节点之间的欧式距离，选择距离最近的节点，并将其和xj定义为一类，选取两节点的中点作为第2 个初始聚类中心点O2；

步骤4设置分类个数k，模糊指数m，容许误差ξ的大小；

步骤5将O1和O2作为初始聚类中心，并设置迭代次数s= 1；

步骤6由式（3）计算样本j属于第i类的隶属度为μij；

步骤7由式（4）计算得到2 个新的聚类中心O1(s+ 1 )和O2(s+ 1 )；

步骤8计算误差，如果e<ξ，迭代结束；否则s=s+ 1，转入步骤6；

步骤9样本归类，将24 个骨架节点划分成两类，并输出类簇中心O1(xu，yu，zu)和O2(xd，yd，zd)。

人体在站立和蹲下时，分别采用改进FCM 聚类算法和传统FCM 算法对24 个骨架节点进行分类，其目标函数J和迭代次数的关系分别如图3、4 所示。站立时，传统FCM 算法需要迭代21 次才能收敛，而改进FCM 算法只需8 次迭代即可收敛。蹲下时，传统FCM 算法需要迭代15 次才能收敛，而改进FCM 算法只需6 次迭代即可收敛。由此可知，改进FCM 算法可以大大提高算法运算速度，增强系统实时性要求。不同人体行为时，对24 个骨架节点进行聚类计算，得到上身中心O1(xu，yu，zu)和下身中心O2(xd，yd，zd) 的分布结果如图5 所示。由图5 可知，骨架节点以人体中心Oc(x1，y1，z1)（1 号节点）为分界点，可以很明显得划分为两类，将两个聚类中心O1(xu，yu，zu)和O2(xd，yd，zd)作为跌倒识别特征数据源，具有较好的识别性和鲁棒性。

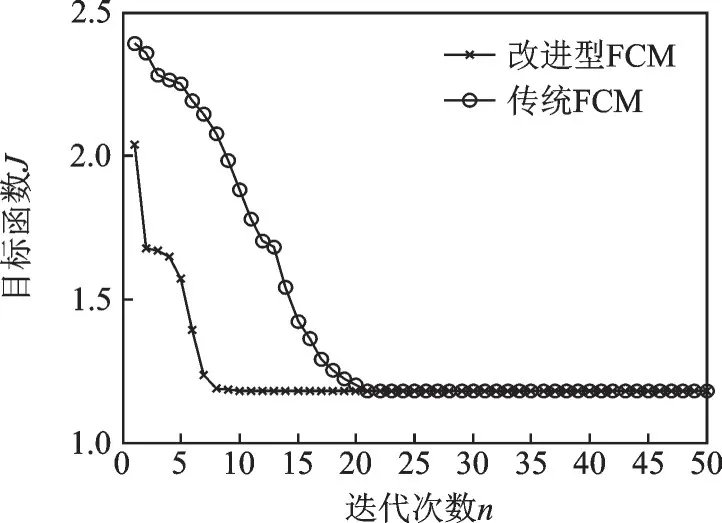
图3 人体站立时改进FCM 和传统FCM 算法比较Fig.3 Comparison of improved FCM and traditional FCM algorithms for a standing state

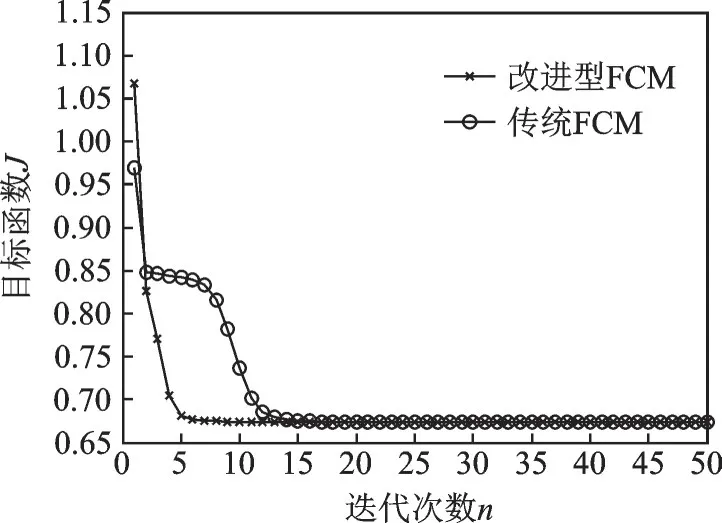
图4 人体蹲下时改进FCM 和传统FCM 算法比较Fig.4 Comparison between improved FCM and tradi⁃tional FCM algorithms for a squatting state

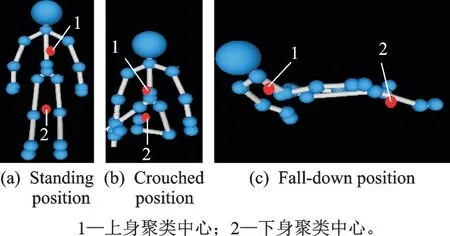
图5 不同人体行为下骨架节点聚类中心结果显示Fig.5 Results of skeleton node cluster center for dif⁃ferent human behaviors

3 跌倒特质数据提取

3.1 归一化高度特征计算

跌倒时，人体各骨架节点距离地面的距离都会迅速变小，尤其是头部高度的变化最为明显，因此选取头部（3 号节点）距离地面的高度作为跌倒检测的阈值条件。由于人体形态差别较大，阈值的选取随不同的人体，变化较大。为增加系统的鲁棒性，对头部节点距离地面的高度进行归一化处理，计算过程如下：

（1）人体的左右脚掌骨架节点15，19 和地面接触，因此将这两个节点的高度默认为零，并以此建立地面方程。首先通过Kinect SDK 获取15 和19 节点的坐标数据，然后将其代入式（5），先计算地面方程和Kinect 之间的倾角θ，进而确定地面方程

（2）地面方程确定以后，将3 号头部节点坐标(x3，y3，z3)代入式（6），计算头部距离地面的高度d3

（3）人体在站立状态下，将人体中心Oc(x1，y1，z1)坐标代入式（6），计算人体中心距离地面的高度d1，并将此高度定义为归一化基准高度。

（4）计算归一化高度dn=d3/d1，并将此作为跌倒识别阈值条件。

选择A、B、C3 个形体差异较大的人作为实验对象，分别采集他们在跌倒、蹲下、弯腰、慢跑和行走5 种状态下的骨架节点数据，并计算dn的平均值，结果如图6 所示。由图6 可知，不同的实验对象在同一种动作下的归一化高度dn变化不大，不同动作下的dn变化比较明显。在跌倒状态下，dn的值在0.1 左右，为防止发生漏判，本文选择dn= 0.25 作为跌倒识别阈值判断条件。

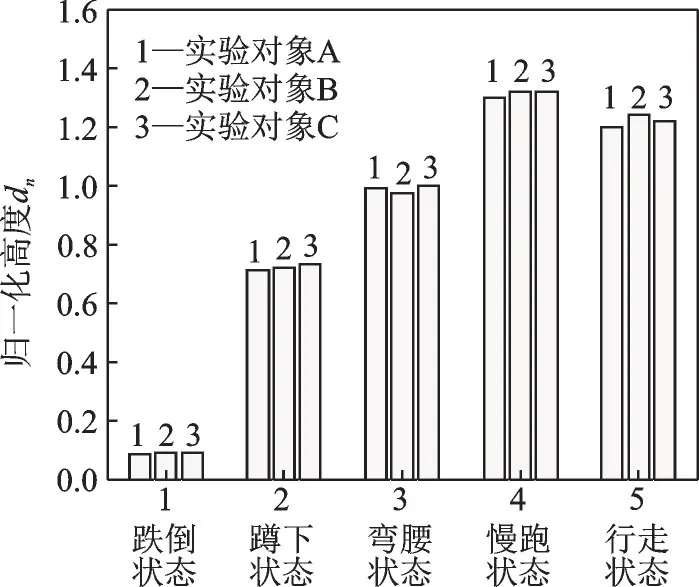
图6 不同体型对象在各动作下的dn 平均值Fig.6 Average values of dn of different body types for each action

3.2 速度特征数据提取

人体在弯腰、蹲下、坐下、跌倒时，各骨架节点距离地面的高度都会发生较大的变化，如果只将高度作为跌倒识别阈值条件，容易造成误判。在弯腰、蹲下、坐下等动作时，虽然高度变化较大，但上述动作发生的持续时间比跌倒发生的持续时间长，因此将速度作为跌倒识别的判断条件，可以很好地区分以上几种动作。

由式（7）可得相邻两帧时类簇中心垂直方向的移动距离dy(i)。两类簇中心的垂直向速度vyu(i) 和vyd(i) 可由式（8）计算得到

式中：y(i)为当前帧时类簇中心的垂直坐标，y(i- 1 )为上一帧时类簇中心的垂直坐标，Δt为相邻两帧的时间差。

图7 为不同动作下，上身中心O1(xu，yu，zu) 和下身中心O2(xd，yd，zd) 的速度变化曲线。由图7 可知，上身中心O1(xu，yu，zu)和下身中心O2(xd，yd，zd)在各动作下的速度都有较大变化，但在跌倒时上身中心的速度变化比下身中心速度变化更加明显。跌倒时的vyu(i) > 1 m/s。因此选取上身中心的速度值作为跌倒识别的另一个阈值条件，为减少漏判选取vyu(i)= 0.9 m/s 作为跌倒识别速度阈值。

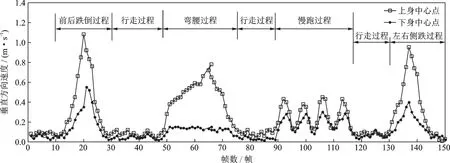
图7 不同动作下两聚类中心速度变化曲线Fig.7 Velocity variation of two cluster centers for different actions

3.3 加速度特征数据计算

研究表明，由骨骼节点位移变化量换算得到的加速度特征参数对基于机器学习的跌倒检测算法具有较好的行为识别性，因此选取上身中心O1(xu，yu，zu)和下身中心O2(xd，yd，zd)在3 个方向上的加速度作为跌倒识别特质向量，输入基于CNN 的跌倒检测模型。聚类中心在x轴方向的速度值由式（9）计算，两聚类中心在x轴方向的加速度ax1(i)和ax2(i)由式（10）计算。同理，分别得到两聚类中心在y轴方向和z轴方向的加速度ay1(i)、ay2(i)和az1(i)、az2(i)

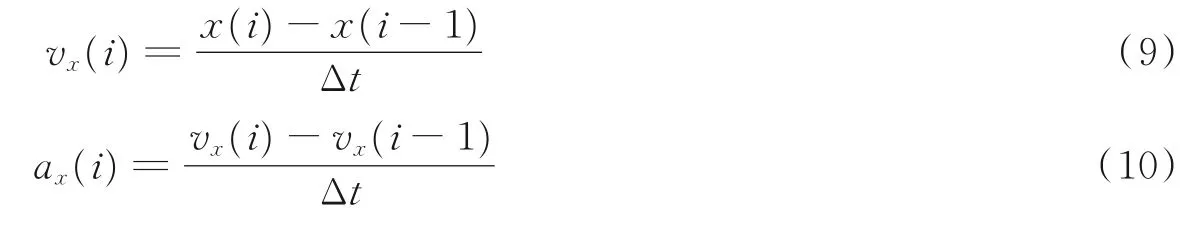
3.4 角度特征数据计算

两个聚 类中心点O1(xu，yu，zu)、O2(xd，yd，zd) 和 人 体 中 心Oc(x1，y1，z1)3 点可围成一个三角形，如图8 所示。三条边分别用L12、L1c和L2c表示，线段L1c和L2c之间的夹角定义为θo，其大小由式（11）计算。式中L12、L1c和L2c的大小可由式（12）计算。将L12和水平方向之间的夹角定义为θh，其大小由式（13）计算

图8 三个中心点几何关系图Fig.8 Geometric relationship of three center points

不同动作时θo和θh的变化曲线如图9 所示，其中，曲线data1 表示θo的大小，曲线data2 表示θh的大小。由图9 可知，在行走和慢跑过程中，θo接近于180º，θh接近于90º，基本没有变化。在跌倒过程中，θh从90º 急剧下降到20º 左右，而θo的变化则不太明显。在弯腰过程中，θo从180º 附近急剧下降到90º 左右，θh也有较大变化，但变化没有θo明显。因此，通过θo和θh可很好地识别跌倒和日常行为，故选其作为跌倒识别特征数据。

图9 不同人体动作时θo 和θh 的变化曲线Fig.9 Variation of θo and θh for different human actions

4 CNN 跌倒识别算法设计

4.1 CNN 跌倒检测模型

对聚类中心的高度和速度进行阈值分析，虽然具有一定的跌倒行为识别性，但识别精度并不高。比如，跌倒、蹲下、坐下等行为的高度和速度特征相似，阈值分析不适合上述行为分类。本文采用CNN算法构建跌倒识别模型。CNN 是一种包含卷积计算且具有深度结构的前馈神经网络，具有良好的表征学习能力。本文设计的跌倒识别算法如图10 所示，为满足CNN 算法对输入样本的格式要求，需将特征数据重构成8×8 的“图片”格式，第1 个卷积层内部包含18 个的卷积核，大小为3×3，用于粗略提取跌倒特征，第1 个池化层的大小选为2×2，步长选为1。第2 个卷积层内部包含36 个的卷积核，大小为3×3，用于精确提取跌倒特征，第2 个池化层的规格和第1 个池化层一样，池化层用来降低特征维度，提高运算速度。将提取的特征输入全连接层运算，通过判断层分类，最后输出识别结果。CNN 一般先采用标准正态分布或均匀分布对权重W和偏置b进行初始化，然后经过训练学习不断优化更新，直到接近或达到目标值。

图10 CNN 跌倒检测模型Fig.10 Fall detection model based on CNN

4.2 样本数据重构

本文提取了跌倒识别加速度ax1，ax2，ay1，ay2，az1，az2和角度θo和θh共8 个跌倒识别特征向量［19］。将采集到的连续8 帧的特征向量重构成一个8×8 的样本数据Si

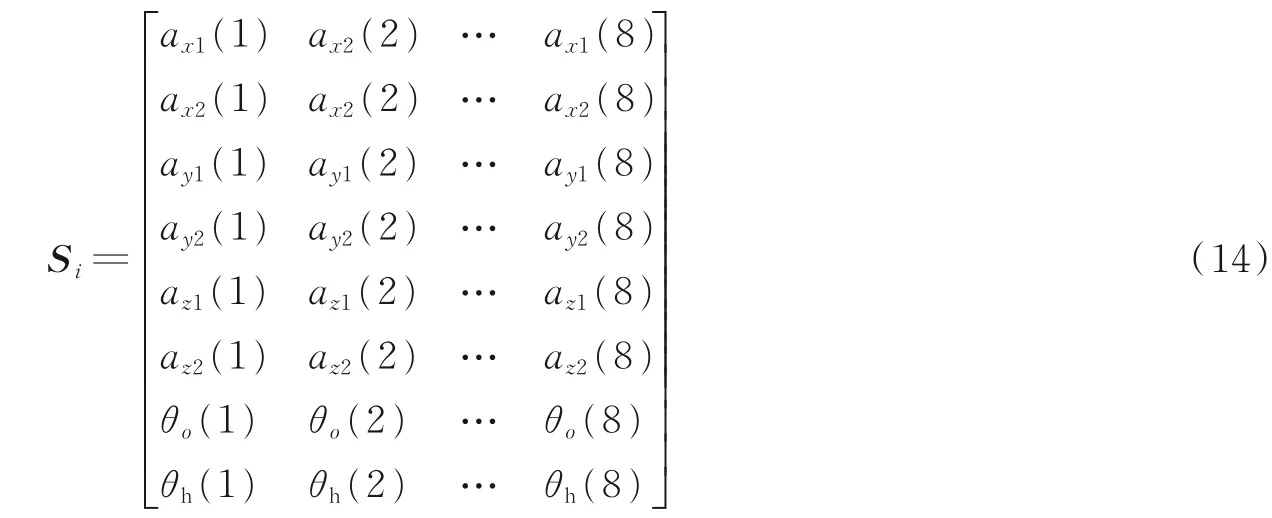
为检验系统的鲁棒性，选择A、B、C 这3 个形体差异较大的实验对象，构建1 000 个训练样本，样本中包含行走、慢跑、弯腰、前后跌倒和左右跌倒动作。将训练样本输入设计的CNN 模型进行训练，训练结果如图11 所示。由图11 可知，训练步长在80 左右时，CNN 已经收敛稳定，训练准确率达100%。

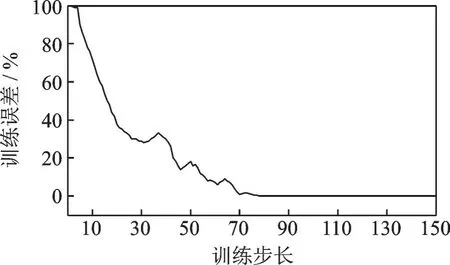
图11 CNN 训练步长和准确率之间的关系Fig.11 Relationship between CNN training step and accuracy

4.3 跌倒检测流程

为保证系统的实时性和识别准确性，采用阈值分析和机器学习相结合的方法来设计跌倒检测系统，检测流程如图12 所示。将采集到的骨骼点数据进行平滑处理，通过改进FCM 算法计算两聚类中心点坐标。将上身聚类中心点O1(xu，yu，zu) 的速度值vyu(i)= 0.9 m/s 作为跌倒识别第一阈值判断条件，若条件成立，则进入归一化高度计算，将dn= 0.25 作为跌倒识别第二阈值判断条件。如果两个阈值条件均成立，则认定人体处于假定跌倒状态，将重构的样本输入CNN 跌倒识别模型，进行跌倒最终认定，如果输出结果为真，则跌倒认定成功，系统进行远程报警。

图12 跌倒检测流程Fig.12 Fall detection process

5 实验结果和分析

选择D 和E 两个不同体型的实验对象，分别模仿向前跌倒、向后跌倒、左侧跌倒、右侧跌倒、坐下、蹲下、弯腰各30 次，共得到420 个检测样本。将采集到的相同样本数据分别通过本文算法，阈值（Threshold value size，TVS）、SVM、强分离器（Adaptive boosting，Ada⁃Boost）、决策树（Decision tree，DT）、KNN 算法进行跌倒识别，检测识别结果如表1 所示。可以发现本系统所采用的识别算法其准确率达到98.8%，而其他算法中识别精度最高的Ada⁃Boost 算法其准确率仅为95.8%，因此本文算法识别精度明显高于其他算法。 本文算法的平均识别时间为0.178 s，略慢于TVS 检测算法的0.083 s，但TVS 算法的识别精度仅86.6%，而另外几种机器学习检测算法中最快的DT 算法其平均识别时间为0.262 s，慢于本文算法，因此本文提出的FCM 改进算法既保持了较高的识别准确率，又保证了系统的实时性要求。

表1 各类算法模型在相同样本数据下的检测结果对比Table 1 Comparison of detection results of various algorithm models under the same sample data

6 结束语

本文采用深度视觉传感器Kinect V2 用于监测跌倒，首先将获取的骨骼节点数据通过FCM 聚类算法进行分类，得到两个聚类中心点。以两聚类中心点坐标和人体中心点坐标为数据分析源提取高度、速度、加速度和角度为跌倒识别特征向量，采用阈值和CNN 相结合的方式实现跌倒识别。结果表明，本文设计的跌倒检测系统具有更高的识别正确率、更低的误报率以及更好的鲁棒性，为老年人跌倒实时监测提供了新的方向。