逆断层黏滑作用下隧道力学行为研究
2021-09-19郭翔宇
郭翔宇, 耿 萍, 丁 梯, 王 琦, 杨 琪, 何 悦
(1. 西南交通大学 土木工程学院, 成都 610031; 2. 交通隧道工程教育部重点实验室, 成都 610031;3. 中铁二院工程集团有限责任公司, 成都 610031)
我国处于欧亚地震带及环太平洋地震带之间,经受多个板块的挤压作用,断裂带孕育。特别是西南地区自2008年汶川地震后[1],板块运动明显进入活跃期。而西南地区在建大长隧道(狮子坪隧道,13.2 km;黄土梁隧道,13.0 km;大峡谷隧道,12.1 km等)及已建大长隧道(锦屏山隧道,17.5 km;米仓山隧道,13.8 km;新二郎山隧道,13.5 km;泥巴山隧道,10.0 km等)众多,相当一部分隧道工程处于青藏高原中东部,位于欧亚板块及印度板块交界,此处新构造运动剧烈,深大活动断裂广泛分布。因此,势必需要考虑活动断层黏滑作用对隧道结构的影响。
目前,关于断层错动对地下结构影响的研究主要集中在数值模拟及模型试验方面。张伟喜等[2]运用数值仿真方法,研究了正断层黏滑错动下隧道衬砌的受力特征,结果表明断层倾角越大,断层黏滑错动下隧道结构的设防长度越小。潘庆等[3]结合某公路隧道,研究了断层错动位移对复合式衬砌的影响,结果表明设置缓冲材料能够很好的改善隧道的受力环境。蒋树屏等[4]提出隧道“铰接设计”中节段长度以及接缝剪切刚度的计算公式,同时分析了接头刚度失效后节段的变形特性。Liu等[5]研发了新型模型箱,研究了松散地层条件下正断层错动对隧道结构的影响,试验结果显示隧道结构的破坏特征及裂缝产生的初始位置均与断层倾角有关。赵坤等[6]采用正交试验研究了不同混凝土材料在隧道铰接设计中的优缺点,认为纤维塑性混凝土具有韧性好、抗拉强度高的优点,适用于隧道节段的柔性连接。王道远等[7]开展1:30的黏滑断层隧道抗错断模型试验,研究了隧道减错缝位置对抗断性能的影响,试验结果指出当减错缝与断层错动面一致时,抗断性能最佳。
既有研究对断层黏滑过程的模拟多是给模型施加一个缓慢的均匀速度、位移时程或者瞬时位错,模型及位错缺乏合理匹配性,无法很好的模拟出隧道结构在黏滑过程中的受力特征。本文以龙门山断裂为工程背景,考虑大尺度时间及空间效应,建立考虑断层面黏结特点的300 km×100 km板块挤压模型,板块运动20万年后将期间获得的断层黏滑位移时程施加到精细有限元模型上,分析隧道结构在逆断层黏滑作用下的衬砌开裂及变形行为。本文研究成果可为相关隧道结构在断层黏滑作用下的变形及破坏特征提供参考。
1 研究方法
隧道结构较之板块,尺度相差太远,建立“隧道结构-板块”数值模型的计算效率较差。故本文参考子模型方法[8],首先建立网格及几何特征较粗糙的全局模型,即板块挤压模型。然后建立关键区域的精细子模型,即跨断层隧道三维有限元模型,将全局模型中对应驱动节点处的位移值作为子模型的附加边界条件。如图1所示。

图1 子模型法示意Fig.1 Sub-model method
既有成果表明,隧道对地层的变形具有追随性[9],故全局模型中未考虑隧道结构。
考虑到逆断层黏滑错动主要为水平挤压以及竖向位错,侧向约束相对较小。又板块尺度较大,建立三维大尺度板块挤压模型的性价比较低,故采用空间大尺度二维板块挤压计算模型获取跨断层隧道三维有限元模型所需边界条件。考虑到板块运动模型和断层错动模型尺寸差异较大(竖向尺寸分别为100 km和100 m),故将板块运动模型断层面地表位置上下盘的水平、竖向位移作为断层错动模型的边界条件整体施加。
2 板块挤压数值模型
龙门山断裂处于四川盆地(欧亚板块)和青藏高原(邻近印度板块)交界,坐落于龙门山址。其西部靠近青藏高原腹地,受到印度板块运动NW-NWW方向的水平挤压。在板块挤压运动的作用下,龙门山断裂有发生逆断层黏滑错动的可能,即上下盘在水平方向发生挤压,在竖直方向表现为上盘向上升,下盘相对下降(图2)。

图2 板块运动下逆断层黏滑错动Fig.2 Slip dislocation of reverse faults under plate movement
为明确板块挤压作用下逆断层黏滑行为,依据龙门山址地质构造建立空间大尺度二维板块挤压计算模型(图3),尺寸为300 km×100 km。为表征岩石圈在断层骤然错动下的刚性特性,又能够体现板块长期运动下的流变特点,地层选用Burgers模型。根据对中国大陆岩石圈的相关研究[10-11]确定各地壳层位置以及相关参数,因篇幅问题不再赘述。

图3 板块挤压数值计算模型Fig.3 Numerical calculation model of plate extrusion
伍吉仓等[12]统计结果显示青藏高原东南缘地壳运动速度场422个GPS观测站水平速度E方向分量值96%位于-5~20 mm/a,其中位于0~10 mm/a之间的站点最多,占61%。庞亚瑾等[13]建立了横跨龙门山断裂带的二维有限元岩石圈剖面模型,其参考龙门山两侧GPS资料,模型左侧边界施加8.3 mm/a水平速度,右侧边界施加7.0 mm/a的水平速度,计算结果较好地反映了青藏高原东缘在重力效应控制下的岩石圈变形特征。柳畅[14]研究成果显示,GPS速度场观测数据表明龙门山断裂带速度场为1~3 mm/a。综上考虑,龙门山断裂带在印度板块作用下,经由青藏高原与四川盆地作用,所受挤压速率在0~10 mm/a,本文取其中间值5 mm/a。据此,模型底面及四川盆地侧设置法向约束,青藏高原侧施加恒定的5 mm/a挤压速率以模拟印度板块的挤压作用,即受到印度板块的挤压作用,某时刻龙门山断裂带可能发生逆断层黏滑。其施加方法为在板块挤压数值计算模型左侧边界上,为其整体施加恒定挤压速率5 mm/a时程曲线。其中,模型以标准单位m建模,故时程的时间单位为秒(s),挤压速率经换算后以速度场(m/s)形式施加。
在挤压速率的影响下,断层面从初始固结到黏滑发生是一个位错逐步累积直至突然增大的过程。故在断层面处设置接触属性,选用能够表征滑动速率对断层面黏结弱化影响的速率弱化模型[15-16]。其摩擦因数与速度的关系为
μ=μd+(μs-μd)e-dc|v|
(1)
式中:v为滑动速率;dc为衰减系数;μd为动摩擦因数;μs为静摩擦因数。
故断层面剪切力τ与摩擦力的关系为
τ≤μ×σn,μ=μs,断层黏结
τ>μ×σn,μ=μd,断层滑动
(2)
动静摩擦因数分别取为μd=0.6,μs=0.1[17-18]。
3 逆断层黏滑作用分析
3.1 逆断层黏滑过程分析
考虑板块运动的大尺度时间效应,板块运动20万年之后,断层面上方剪切应力时程如图4所示。
图4中仅选取剪切应力突变及后续时刻,时程曲线的每一次突变即剪切应力发生“骤降-再回升”。这是由于板块挤压作用下断层面首先发生蠕滑,伴随断层蠕滑量的不断提高,断层错动速度加快,断层接触面区域摩擦系数不断降低,地层上盘与下盘之间的摩擦阻力不断降低,断层在某时刻突然产生大位错。此刻断层面处滑动速率到达最大值,剪切应力骤然降低。然后,伴随着断层面位置累积能量的逐步消散,断层位错逐步趋于稳定,上盘与下盘之间的剪切作用逐渐得以恢复,断层面位置剪切应力再次增大回升。综上,图4所示断层面位置剪切应力的每次“骤降-再回升”过程即代表一次逆断层黏滑事件。
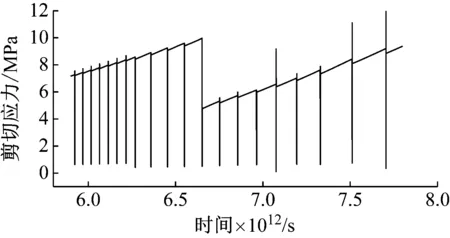
图4 剪切应力时程图Fig.4 Shear stress time history diagram
由图4所示,初期断层黏滑事件的复发周期较小,后期越来越大。经统计黏滑事件可知,当板块以5 mm/a挤压速率运动时,龙门山断裂的断层黏滑复发周期位于3 170~5 866年之间,同现有2 000~5 000年的研究成果基本吻合[19-20]。
提取上下盘顶部邻近断层处位移时程然后进行矢量求差,可得断层面位置竖直和水平的位错时程(图5)。
由图5可知,上下盘位错发生时间与图3中剪切应力突变时间基本一致,这说明位错的产生总伴随着剪切应力的突变。竖直及水平位错量处于0.2~2.5 m之间,还有小于10 cm的微量错动事件,即断层黏滑并非总伴随大位错产生。
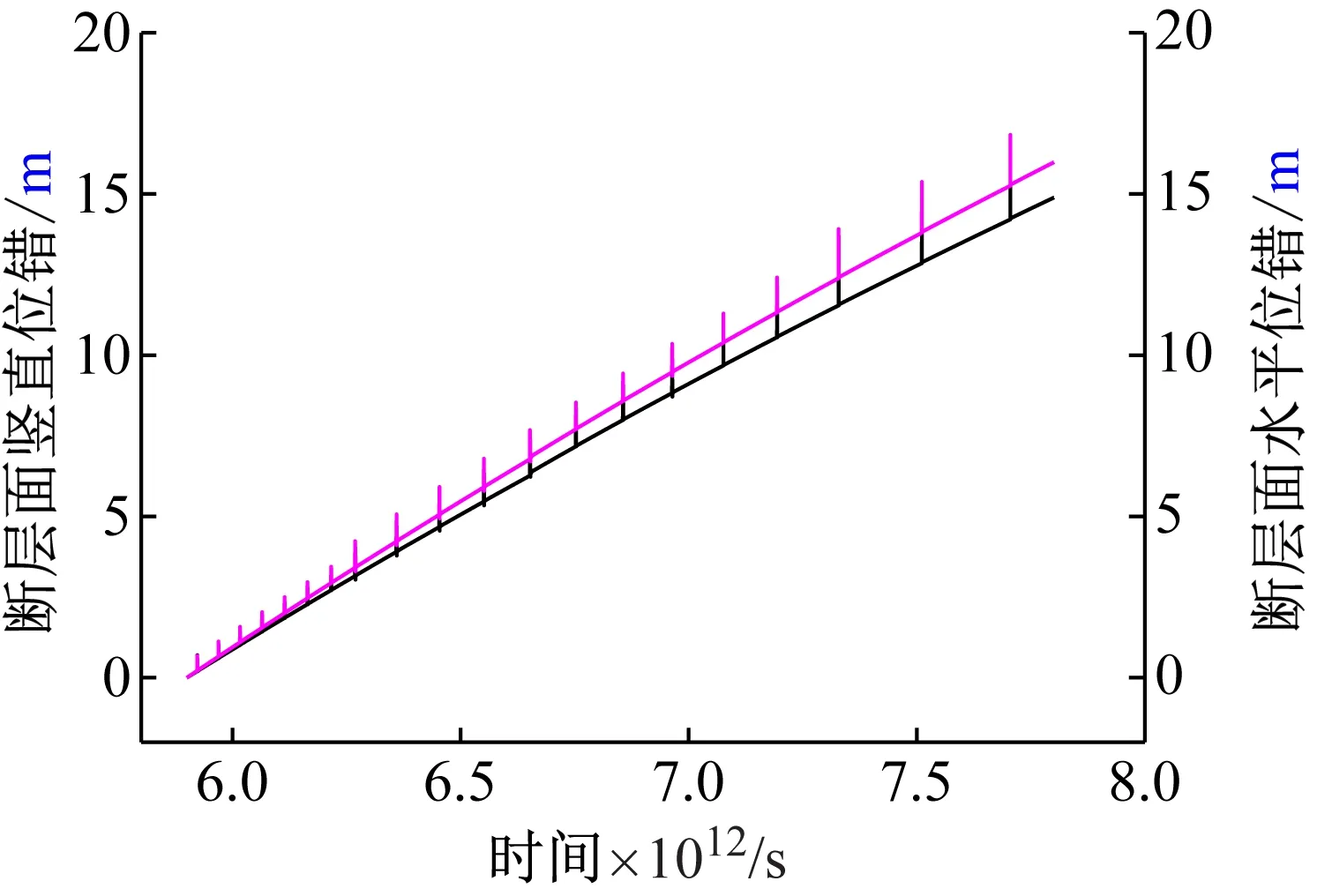
图5 断层顶点位错时程Fig.5 Time history of fault vertex dislocation
上盘顶面水平及竖向加速度、速度时程如图6。
由图6总体可见水平及竖向速度、加速度的产生时刻基本一致。就速度时程而言,上盘水平及竖向速度时程均体现出明显脉冲特征。由具有代表性的5次加速度峰值点可见,其(时间s,竖向加速度峰值m/s2,水平加速度峰值m/s2)分别为(6.29,-0.17,-0.09),(6.50,-1.74,-0.56),(6.73,-2.98,-1.54),(7.05,-21.32,-8.24)以及(7.71,-15.27,-5.96)。竖向加速度与水平加速度的比值分别为0.9, 3.1, 1.9, 2.6, 2.6。由此可见,随着板块运动的逐步累积,板块发生黏滑错动,黏滑时刻里竖向加速度峰值基本大于水平加速度峰值,且比值大部分位于2.6左右,即近场地震动竖向分量效应[21]明显。
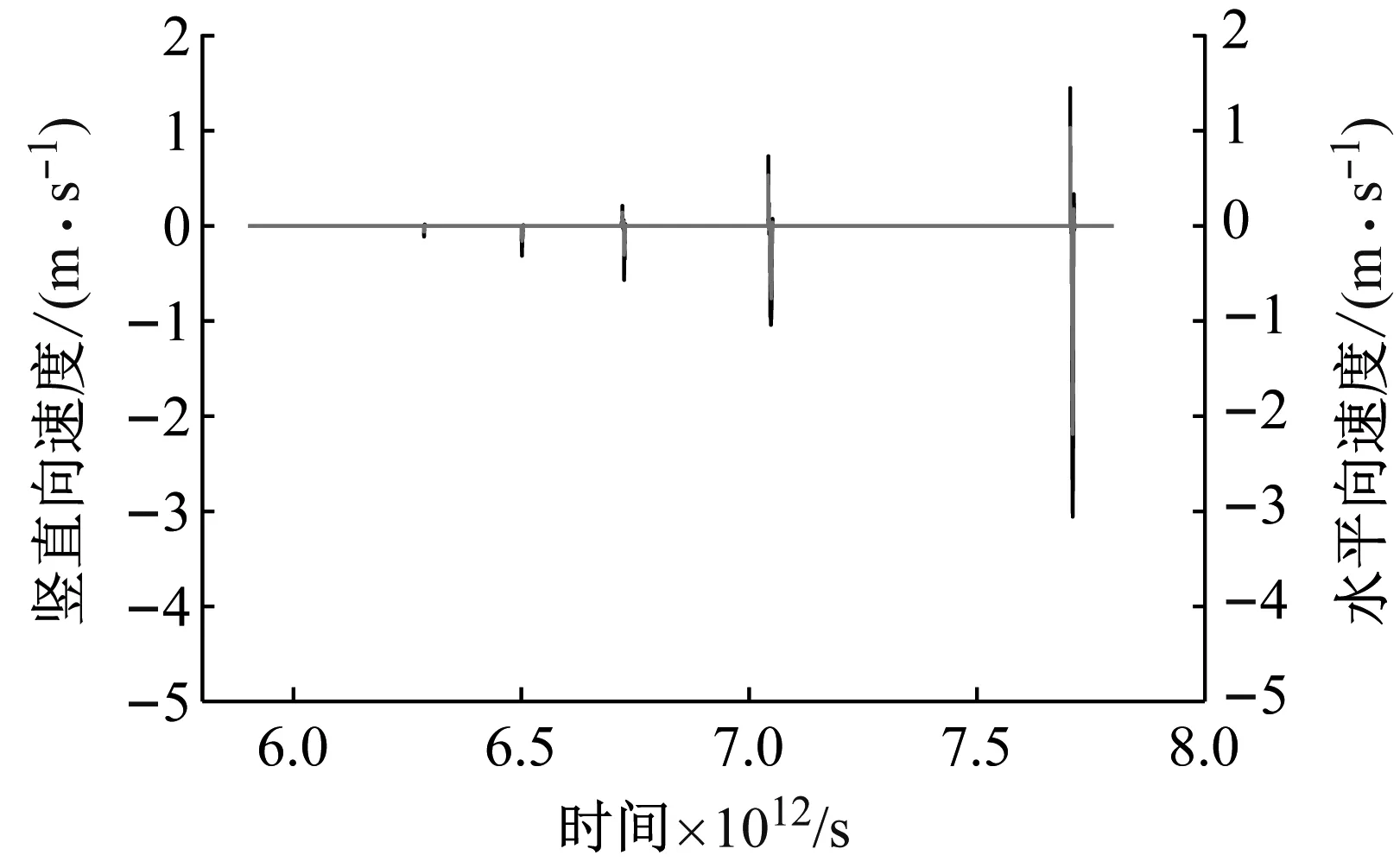
(a) 速度
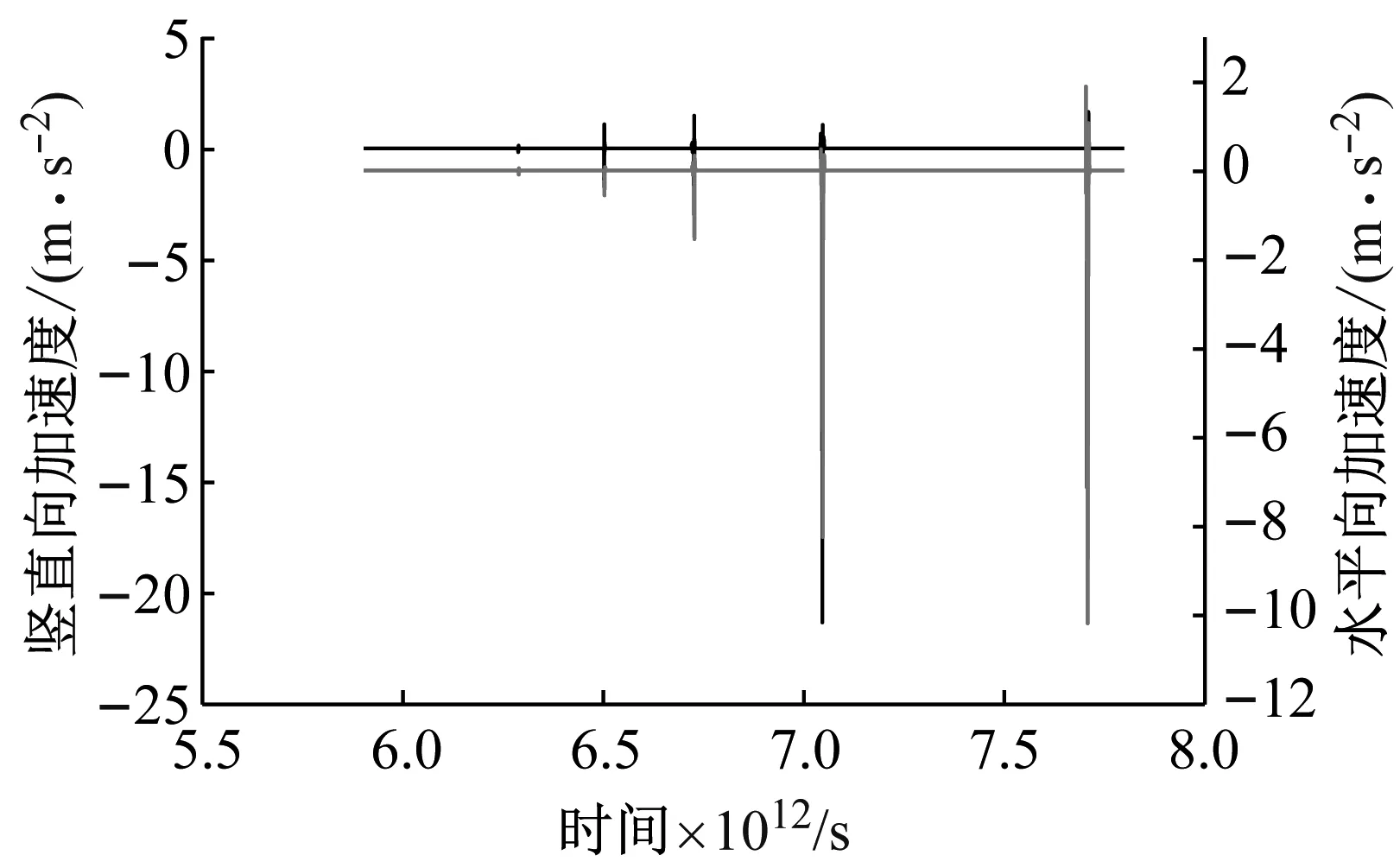
(b) 加速度图6 上盘顶点处时程曲线Fig.6 Time history curve at the apex of the upper plate
与图4、5相比,图6在各个黏滑时刻并未都反映出高加速度峰值的特点。经过对相应时间点进行分析研究,每个黏滑时刻都表现出一定的瞬时加速度,但大部分位于0.1 m/s2以下,即并非每一次逆断层黏滑事件均有较大加速度产生。
3.2 黏滑时刻位移特征曲线
根据图4表征的黏滑过程,调出各黏滑事件的位移时程并进行时间点归零处理,获得各时刻黏滑事件的位移特征曲线,可以发现位移特征曲线主要归为两种类型,代表性曲线如下(图7)。

(a) a类

(b) b类图7 逆断层黏滑时刻位移特征曲线Fig.7 Displacement curve of reverse faults
依照特征曲线形态,将其分为不同阶段。对于a类位移特征曲线而言,其位移展开过程可以分为两个阶段,在Ⅰ阶段即错动初始,上下盘位移迅速展开,0.75 s之后达到位移峰值。随后,在Ⅱ阶段逐渐降低,最后保留一部分永久位移,整个过程中位移仅有一个峰值,特征曲线呈现单峰值特点。
对于b类位移特征曲线而言,其位移展开过程可以分为三个阶段,在Ⅰ阶段位移持续增大、展开相对缓慢;经12.91 s达到峰值后,时程曲线进入Ⅱ阶段,位移持续减小,减小速度较快;经5.88 s后,位移停止降低,开始回弹,在略有增大后保留永久位移,最终位移小于Ⅰ阶段所产生的位移峰值,特征曲线呈现双峰值特点。
获得逆断层黏滑时刻位移特征曲线后,建立跨越黏滑断层的隧道数值模型,将特征曲线施加到数值模型上,研究逆断层黏滑作用对隧道结构的损害。
4 跨断层隧道计算模型
拟定隧道穿越倾角与图3一致的黏滑断层,模型纵向200 m、宽度100 m、高度100 m,隧道跨度12.5 m,高度9.6 m,衬砌厚度0.5 m(图8)。
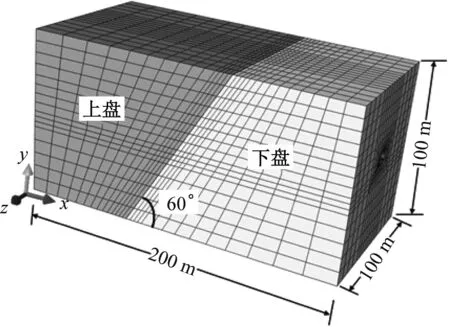
图8 三维有限元模型Fig.8 Three-dimensional finite element model
“上盘-下盘”、“围岩-衬砌”之间法向选用硬接触,切向采用摩擦接触。
拟选用三类地层,地层采用Mohr-Coulomb本构,基本参数由JTG/T D70—2010《公路隧道设计细则》[22]所推荐围岩参数拟定。考虑到隧道衬砌结构的损害主要由断层黏滑错动引发,在此将上盘及下盘拟定为同一类地层材料。隧道衬砌结构采用C35混凝土。基于扩展有限元理论[23]取混凝土断裂能为80 N/m[24],隧道衬砌开裂特性选用最大主应力原则,混凝土抗拉强度取设计值1.57 MPa。以上各物理力学参数见表1。

表1 基本物理力学参数Tab.1 Basic physical and mechanical parameters
如图9所示,将3.2节中所获得的黏滑时刻位移特征曲线施加到地层上,约束上下盘侧面的法向(Uz)位移,地表自由。

图9 边界约束条件Fig.9 Boundary constraint
5 逆断层黏滑作用下隧道受力特性
5.1 衬砌开裂行为研究
施加形态更为复杂的b类位移特征曲线以观察衬砌结构的开裂行为。显然的,当竖向峰值位移太小时,隧道结构不发生破坏;过大时,隧道结构将坍塌,同样无法很好的反应破坏特征。本文为研究不同地层条件下隧道结构的破坏特点,将竖向位移峰值选定在一定范围内,使得计算结果能反应破坏规律而隧道不完全坍塌。孙萍等[25]研究显示当土体上下盘底部竖向错距由10 cm增大到93 cm时,管道纵向最大拉应力由0.65 MPa增大到18.43 MPa,管道发生局部破坏。左娟花等[26]统计结果显示,1978年日本伊豆大地震中稻取隧道的竖向错位达50 cm,隧道拱顶衬砌脱落、破坏,受损严重。孟振江等[27]研究显示,当上盘沉降量达到50 cm时,相邻分段隧道产生拉张、位错破坏。由此可见,当竖向位移峰值处于50~100 cm之间时,隧道结构出现严重破坏,以此取值计算模型可较好的反映隧道的破坏特征。故调整竖向位移峰值为80 cm。
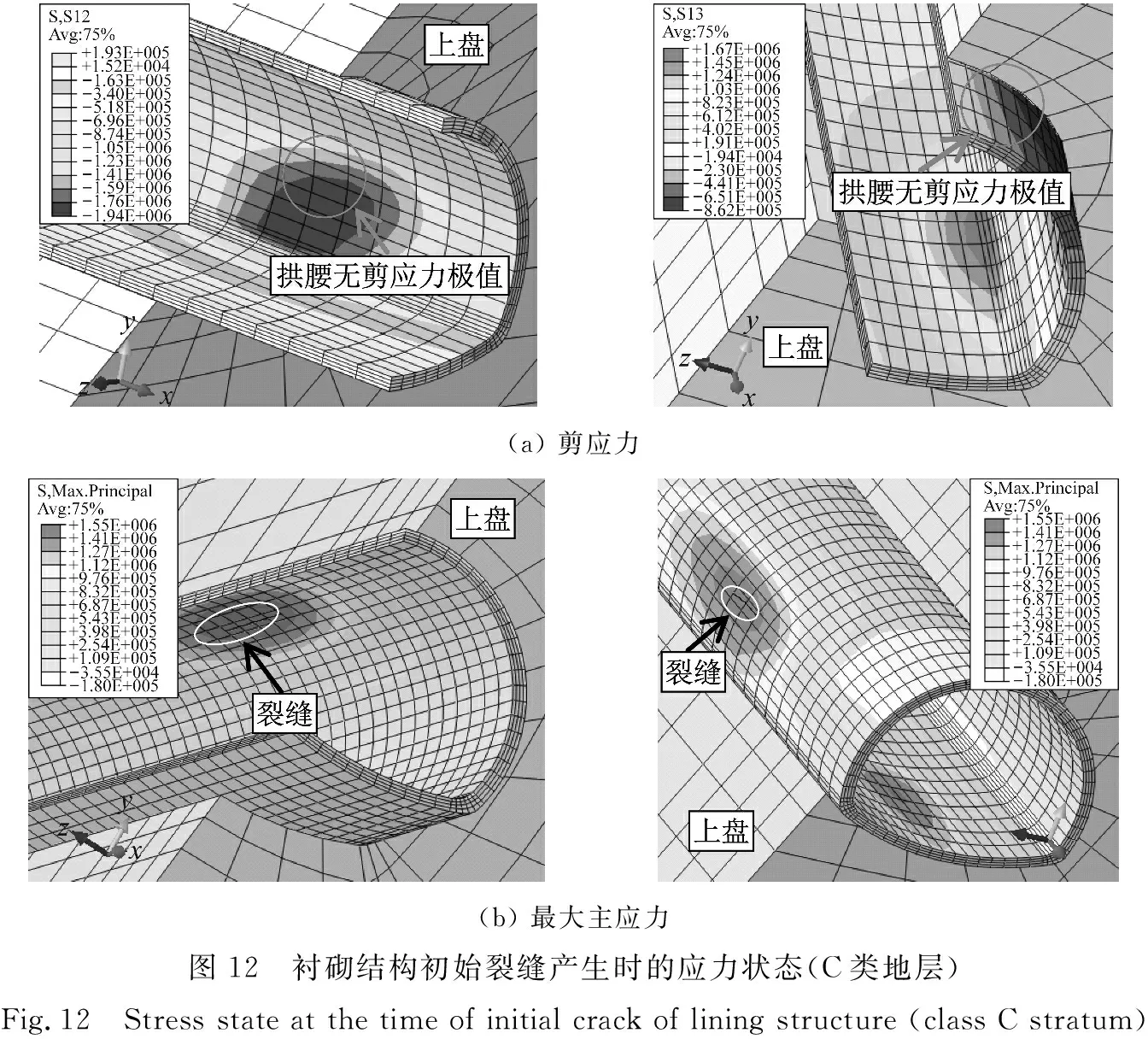
分别在1.93 s、3.36 s、4.64 s,三类地层条件下隧道结构出现初始裂缝,且裂缝沿隧道拱顶-拱底竖向面呈对称分布,此时衬砌应力状态如图10~12。A、B、C三类地层条件下隧道沿z、y方向(s13、s12)剪切应力极值分为(1.2,2.2)MPa、(2.2,1.5)MPa、(1.9,1.7)MPa,剪应力极值呈现2.2 MPa—2.2 MPa—1.9 MPa降低。即随着地层刚度降低,衬砌所受剪切作用有所削弱。
由图10可知,A类地层条件下隧道衬砌结构剪应力和最大主应力极值位于同一处,又对比三种地层条件下最大主应力极值基本一致(1.5 MPa)且A类地层条件下裂缝出现时间明显最早(1.93 s),由此可知A类地层条件下隧道衬砌结构的裂缝主要是逆断层错动引起的剪切作用导致。
相对而言,初始裂缝产生时B类地层的剪应力峰值同A类近似,且拱脚处(初始裂缝位置)出现剪切应力s13的应力峰值。同时,该裂缝距断层面较远(3 m),断层错动时隧道发生一定纵向弯曲,可知此时隧道横断面所受较大的纵向弯矩。即断层面剪切以及隧道纵向弯曲共同作用导致B类地层条件下衬砌结构产生开裂。
C类地层刚度最小,当衬砌结构产生初始裂缝时断层面区域隧道衬砌结构的剪切应力极值依然较小(1.94 MPa),而且衬砌结构初始裂缝位置的剪切应力相对更小(拱腰、拱顶未出现剪应力极值)。故C类地层条件下衬砌的开裂基本不由逆断层错动的剪切作用引起,而是竖向位错的增大使隧道纵向弯曲增大,进而拱顶以及拱腰区域产生较大的局部弯矩,最大主应力增大导致衬砌开裂。
随着逆断层位错逐步增大,隧道衬砌结构的后续裂缝拓展均在初始裂缝位置上进行,且裂缝的最大张开量始终位于初始裂缝处。考虑到裂缝及结构的对称特点,仅对其一进行分析。各工况裂缝宽度最大张开量时程曲线如图13所示,其中C类地层条件下衬砌结构有拱顶(#1)、拱腰(#2)两条裂缝。
在错动位移作用下,不同地层条件下裂缝张开量均表现出先增大、后减小、再回弹、最终保留一定张开量的趋势。其中,当地层刚度较大时,此变化趋势更加明显。同时对比三个阶段的分界线,可见相对图7(b)而言,由图13可见,位移特征曲线I阶段与Ⅱ阶段的分界线并未在衬砌最大裂缝张开量的极值点处,且A类地层中衬砌裂缝张开量极值出现最早,在分界线左侧;C类地层裂缝张开量极值出现最晚,在分界线右边。可能的原因有二:① A类地层刚度最大,地层变形最小,相同边界荷载下隧道变形最早。同理,C类地层条件下隧道变形最晚;② A类地层条件下衬砌裂缝主要由断层错动剪切作用引起,C类地层条件下衬砌裂缝主要由地层挤压导致衬砌局部弯矩引起,两者裂缝产生及发展机理不同。大刚度地层剪切作用下,衬砌结构变形较为剧烈,在地层位错极值前裂缝宽度便达到最大。小刚度地层挤压作用下,地层变形较为舒缓,裂缝宽度极值出现时机较晚。而B类地层刚度位于以上两者之间,故其衬砌破坏变形机理以及裂缝宽度出现时机,均位于A、B两类地层之间。
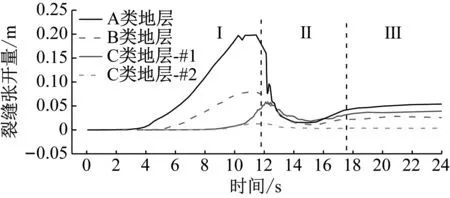
图13 衬砌最大裂缝宽度时程曲线Fig.13 Time history curve of maximum crack width of lining
断层错动完成后,不同地层条件下隧道衬砌的开裂形式如图14~16所示。可以看出,不同地层条件下衬砌裂缝拓展方向及长度不尽相同,但均为对称分布。其中,A类、B类地层中衬砌结构有两条裂缝,均邻近或到达仰拱;C类地层中衬砌有三条裂缝,均未对仰拱造成破坏。
就裂缝形式而言,对于A类地层,其为拱腰处出现大角度斜向裂缝。都江堰-汶川公路紫坪铺隧道工程穿越软硬岩互层(属Ⅲ类围岩),对应A类地层,“5·12”汶川地震导致本隧道发生破坏,震害显示隧道拱腰出现大角度的斜向裂缝,与数值计算结果具有一致性。
对于B类地层,其为拱腰至仰拱处有小角度斜向裂缝。刘学增等[28]试验成果显示,逆断层黏滑作用下,当地层剪切模量为0.5 GPa(折合弹性模量1 300 MPa),对应B类地层时,其产生的裂缝倾角较小,同样位于隧道两侧衬砌及仰拱,与本文数值计算结果基本相符。
对于C类地层,其为在拱顶及拱腰有趋近水平的裂缝。胡辉[29]试验成果显示,当采用Ⅳ围岩,即对应C类地层时,断层位错作用下衬砌拱顶内侧及拱脚外侧出现水平裂缝并贯通,与本文数值计算结果具有较好的一致性。
统计不同地层条件下衬砌结构开裂特征,结果见表2。

表2 衬砌结构开裂特征统计表Tab.2 Statistical table of cracking characteristics of lining structures
从表2可见,随着地层刚度的降低,最大裂缝宽度逐渐减小,且初始裂缝产生位置逐渐远离断层面,但裂缝的最终长度随地层刚度降低而增大。这说明地层刚度愈大,逆断层错动产生的剪切作用愈明显,邻近断层区域隧道衬砌的局部变形愈加明显,衬砌裂缝最大张开量也愈大,故A类地层中出现最大衬砌裂缝宽度为19.8 cm;地层刚度愈小,隧道纵向弯曲变形的范围愈广,衬砌裂缝扩展长度也愈长,故C类地层中出现最大衬砌裂缝长度为55.4 m。
5.2 隧道及围岩变形状态分析
逆断层黏滑错动作用下隧道结构以及围岩的变形状态如图17,各变形指标见表3。

注:图中符号及文字分别表示:j-地层编号(A、B、C);Lj-隧道纵向变形范围(隧道与围岩的脱空分离区);βj-裂缝走向与隧道轴线夹角;Dj-围岩最大挤压变形量;“☆”-衬砌初始裂缝位置。图17 隧道及围岩的变形示意图Fig.17 Schematic diagram of deformation of tunnel and surrounding rock

表3 隧道及围岩的变形参量Tab.3 Deformation index of tunnel and surrounding rock
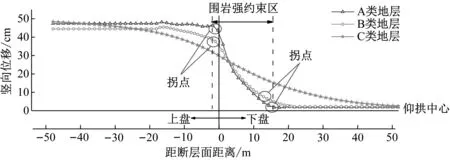
位错完成后,断层面100 m范围内隧道拱顶以及仰拱中心的竖向位移如图18所示。显然,断层的存在会影响隧道的纵向变形,不同地层条件下隧道所受围岩的约束效果有所不同。A、B两类地层条件下位移曲线邻近断层位置有明显拐点,这说明地层刚度较大时围岩挤压变形较小(DA 对于裂缝而言,当地层刚度较大时,围岩对隧道的约束效果较强,上盘与下盘的挤压效果以及断层错动的剪切作用使得隧道衬砌的局部变形更加明显,衬砌结构的开裂主要由断层错动带来的剪切作用或者剪切作用引起的隧道衬砌的局部弯矩所导致,裂缝趋向于沿隧道横断面方向扩展(图14),故βA最大。当地层刚度较小时,断层产生的局部剪切作用较弱,衬砌开裂主要由隧道纵向弯曲所导致的衬砌局部受弯产生,裂缝趋向于沿隧道纵向扩展(图16),βC最小。即地层刚度越大,裂缝扩展方向越趋近于逆断层角度(60°);地层刚度越小,裂缝拓展越趋近水平。在抗震设防设计中,应考虑逆断层的断层角度拟定设防长度。 图18 拱顶及仰拱竖向位移分布Fig.18 Vertical displacement distribution of vault and inverted arch 综上,就竖向位移峰值对衬砌结构开裂及破坏的影响而言,由图13可见,随着竖向位移峰值的逐步增大,衬砌裂缝随之增大。而由图14~图16并结合表3可见,当地层刚度较大时,随着竖向位移峰值增大,衬砌结构受地层剪力作用明显,衬砌首先在拱腰内侧开裂,并沿断层倾向延伸破坏;当地层刚度较小时,随着竖向位移峰值增大,衬砌结构受地层挤压效果明显,衬砌首先在拱顶内侧及拱腰外侧开裂,并沿隧道纵向延伸破坏。 本文以龙门山断裂带为工程背景,首先建立了考虑大尺度时间及空间效应的板块挤压计算模型,然后将获取的黏滑时刻位移时程曲线施加到精细有限元模型上,获取衬砌结构及围岩的受力变形特征。所得结论如下: (1) 在板块挤压作用下,断层面处先产生蠕滑,随着蠕滑的增大,上下盘之间的摩阻力不断降低,在某时刻产生突然性大位错,此时断层面剪切应力骤降。随着位错的稳定,剪切力又发生回升。因此,每次黏滑事件均对应剪切应力 “骤降-再回升”的现象。统计剪切应力变化周期可知龙门山断裂的黏滑复发周期在3 170~5 866年之间。 (2) 黏滑时刻地层位移特征曲线基本可以分为两类。对于a类特征曲线,其上下盘位移展开较快,在0.75 s达到唯一峰值点,然后位移逐渐降低最终保留部分永久位移;对于b类特征曲线,其上下盘位移展开相对较慢,在12.91 s到达第一个峰值点后位移开始降低,5.88 s后位移停止降低开始回弹,最终位移小于第一个峰值点位移。 (3) 地层刚度不同,初始裂缝产生位置不同。随着地层刚度的降低,最大裂缝宽度逐渐减小,但裂缝的最终扩展长度随地层刚度降低而增大。衬砌最大裂缝宽度为19.8 cm,最大扩展长度为55.4 m。 (4) 不同地层条件下隧道所受围岩的约束作用不同,综合A、B两种工况,围岩强约束区长度是隧道跨度的2.88倍。地层刚度较大时断层面处围岩对衬砌的局部约束较为显著,裂缝趋向于沿断层倾角方向扩展;刚度较小时隧道纵向弯曲范围较大,裂缝拓展趋近水平,即有βA>βB>βC。 (5) 不同地层条件下,隧道结构应采用不同抗错措施。对于刚度较大的A类地层,衬砌破坏主要由断层错动的剪切作用引起,应采用柔性抗错措施(铰接设计等),以降低地层剪切效果。对于刚度较小的C类地层,衬砌破坏主要由衬砌局部弯矩引起,应采用刚性抗错措施(钢纤维混凝土等),以强化衬砌强度。对于刚度居于中间的B类地层,应根据具体情况考虑刚、柔性抗错措施的应用。此外,从减小断层位错传递至隧道衬砌的角度考虑,可采用隧道断面扩挖并在外层填筑柔性层的方法。
6 结 论
