切向内力对偏心旋转圆环自由振动的影响

2021-09-19王姚志豪王世宇李海洋

振动与冲击 2021年17期

王姚志豪，汪菲，王世宇,2,3，李海洋

(1.天津大学机械工程学院，天津 300354；2.天津大学机构理论与装备设计教育部重点实验室，天津 300354；3.天津大学天津市非线性动力学与控制重点实验室，天津 300354)

由于结构稳定、受载均衡及视觉美观，在工程领域广泛应用各类旋转部件，以实现驱动、传动、承载和能量转换等功能，如汽车轮毂、滚动轴承和旋转电机等。由于制造安装误差以及应用场合对运动形式的特殊要求，该类部件不再做理想的定轴转动，呈现偏心旋转状态。在高速工况下，偏心旋转可产生显著的离心力，进而引发振动和噪声，降低工作效率，甚至造成永久破坏。本文针对该类部件中的旋转环状结构，开展了内力计算、模态特性和动力稳定性方面的研究。

为了建模和分析方便，现有研究通常假定该类结构绕其对称轴定轴转动。Huang等[1]研究了旋转圆环的振动特性，比较了静环动载与动环静载的计算结果，分析了科里奥利加速度对受迫响应的影响。Wu等[2]采用微元法建立了旋转圆环的面内振动模型，探讨了固有频率分裂及振型耦合规律。Huang等[3]基于行波动力学方法，深入研究了旋转圆环的自由振动特性。夏营等[4]采用多尺度法分析了机、电、磁多场耦合的感应电机定子参激振动问题，并给出了解析形式的不稳定边界。李凤云等[5]将弹性薄环等效为曲梁，建立了刚壁撞击回弹下的动力学模型，分析了各阶模态下的振动特性。张文虎等[6]基于滚动轴承动力学理论，建立了高速圆柱滚子轴承的非线性动力学方程，分析了工况与结构参数对保持架振动特性的影响。

近年来，一些学者开始考虑偏心运动对旋转部件振动行为的影响。岳二团等[7]研究了永磁电机转子系统在气隙偏心下的振动特性，深入分析了不同的偏心与负载类型与振动行为之间的关系。Hashemi等[8]研究了偏心微转轴的三维弯曲振动，应用伽辽金方法得到了解析形式的固有频率，还分析了质量偏心分布与振动行为之间的关系。但是，针对环状结构的研究工作还相对较少。Wu等[9]考虑了离心力与科里奥利力，同时计入偏心旋转产生的不均匀初始应力，深入研究了偏心旋转圆柱薄壳的颤振失稳现象。Liu等[10]采用多尺度法研究了偏心旋转复合材料层合圆柱壳的非线性振动，揭示了偏心率等几何参数对动力学行为的影响规律。

本文研究了偏心旋转圆环的自由振动规律。首先，采用微元法与叠加原理计算内力分布，并根据Hamilton原理建立动力学模型，然后应用经典振动理论计算特征值，预测模态特性与动力稳定性，且与不考虑切向内力的情形进行对比。最后利用数值方法验证了结果的正确性。

1 数学建模

1.1 模型描述

图1为偏心旋转圆环的数学模型，图中该结构绕几何形心o以角速度Ω自转，同时绕偏心o′以角速度Ωa沿刚性轨道公转。o-rθz与o′-rθz分别为随动坐标系与惯性坐标系，极点位于几何形心o，极轴沿连心线o′o方向。p(n)(n=0,1,2,…)为中性圆上的任意一点，v和u分别表示该点的径向和切向位移，er、eθ和ez分别表示径向、切向及轴向单位矢量。中性圆半径、偏心半径、偏心距、轴向厚度、径向厚度、杨氏模量和密度分别为R、RΔ、d、b、h、E和ρ。

图1 偏心旋转圆环数学模型Fig.1 Mathematical model of the eccentrically rotating ring

1.2 切向内力分布

根据简单的运动学关系，可知圆环的自转与公转转速满足

(1)

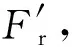
(2)

(3)

图2 偏心旋转圆环受力分析Fig.2 Forces on the eccentrically rotating ring

故p处的离心力在坐标系下的分解为

(4)

(5)

此外，轨道对圆环的支反力为

(6)

本文采用叠加方法[11]计算圆环的切向内力。图3(a)为计算模型，圆环在θ=0处受一个指向圆心的径向集中力Fef1，中性线上分布着均匀的若干虚拟力Fff1,(n)与之平衡。为研究应力分布，截取p处微段dθ进行受力分析，如图3(b)所示，其中Fsf1、Ftf1和Mbm1分别表示剪力、切向内力和弯矩。

在集中力Fef1作用下，微段dθ将产生均布虚拟力

(7)

在图3(b)中，将该虚拟力沿切向和法向投影，同时对微段中心取矩，可得

(8)

将式(8)化简并略去高阶微量，仅考虑剪力Fsf1，有

(9)

切向内力及弯矩与径向、切向变形之间满足[12]

(10)

式中,μ为泊松比。根据圆环的受力特征，可得如下边界条件

(11)

采用算子法[13]求解式(9)，可得径向力集中力作用产生的圆环内力分布

(12)

用Fsf2、Ftf2和Mbm2分别表示微段所受剪力、切向内力和弯矩，有

(13)

考虑式(10)与边界条件

(14)

可得内力分布

(15)

由式(12)和(15)可知，径向与切向集中力分别引起的切向内力分布为

(16)

(17)

根据式(16)和(17)，可直观地得到圆环上不同位置的切向内力，如图5所示。

结合上述分析，偏心旋转圆环的切向内力可表示为

Fθ=Fθv+Fθu+Fsv

(18)

式中,Fθv、Fθu和Fsv分别表示由离心力的径向和切向分量以及轨道支反力引起的切向内力分布，且有

(19)

(20)

Fsv=fθ1(θ)Fs

(21)

(22)

根据式(22)绘制偏心距与切向内力的关系，如图6所示。显然，图中圆环处于拉伸应变状态，其切向应变峰值出现在连心线方向。对于定轴转动情形，圆环仍处于拉伸应变状态，但切向内力呈标准的圆形分布。

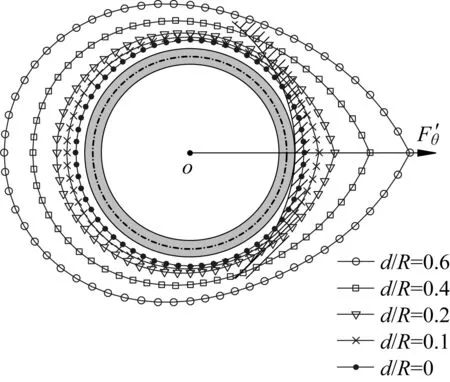
图6 偏心距对切向内力的影响Fig.6 Effect of eccentricities on tangential internal force

1.3 能量表达

在图1所示惯性系下，圆环中性线上任意一点p处的位置矢量可表示为

o′p=(R+v+dcosθ)er+(u-dsinθ)eθ+wpez

(23)

点p在惯性坐标系下的绝对速度va可表示为

va=ve+vc

(24)

式中:ve为点p相对于随动系的速度;vc为随动系相对于惯性系的速度(牵连速度)，且知

因此圆环的动能可表示为

(25)

由图(6)可知，偏心旋转使圆环产生膨胀效应。该结构的势能包括由离心力引起的应变能和弹性振动引起的应变能。在平面应变状态下，圆环上任意点p处的切向应变为

εθ=εθ0+(r-R)εθ1

(26)

式中

则势能可表示为

(27)

式中,A和I分别为圆环截面的面积(A=bh)和主惯性矩(I=bh3/12)。

1.4 数学模型

根据Hamilton原理，可得

(28)

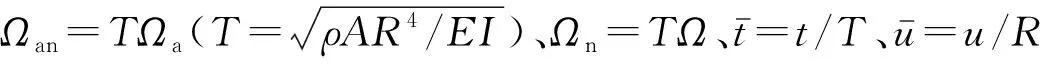
(29)

式中

式中：M1、G1、K1和F分别为质量矩阵、陀螺矩阵、刚度矩阵以及激励向量；D1为支反力产生的附加刚度矩阵。

2 数值仿真

采用伽辽金方法进行响应设解并将式(29)离散。为此，选取一个满足圆环边界条件的形状函数einθ，构造径向与切向振动位移响应[14]

(30)

(31)

式中,xu(t)、yu(t)、xv(t)和yv(t)均为时间的实函数。定义内积运算

(32)

将式(32)代入系统动力学方程，然后与einθ作内积并分离实、虚部，整理可得

(33)

式中

为了预测振动规律，可根据式(33)计算特征值。为此，首先假设

(34)

则

(35)

式中，I为4×4单位矩阵。假设x(t)=eλty，式中λ为系统特征值，y为振型。则特征方程为

(36)

根据式(36)和表1所述参数，可预测系统的稳定性。

表1 旋转圆环基本参数Tab.1 Specifications of a rotating ring

图7描述了是否考虑切向内力的不同情形下特征值随公转转速变化的规律，其中图7(a)和(b)中的实线与虚线分别为前行波与后行波模态。可以看出，系统在两种情形下均存在不稳定问题，且仅与一阶振动相关。根据经典振动理论，如果特征值实部大于零，系统将出现不稳定现象。由图7(c)可知，考虑切向内力的特征值实部具有更小的波峰，系统的稳定性增强。图7(d)表明减小偏心距有利于提高系统的稳定性。

图8描述了公转转速和偏心率对不稳定域的影响。由图7(a)可知，在考虑切向内力的情形下，前行波模态的一阶特征值虚部为零，因此图8(a)为发散不稳定。相比之下，如果不考虑切向内力，根据图7(b)可知，前行波模态的一阶特征值虚部不为零，因此图8(b)为颤振不稳定。对比图8(a)和(b)可以发现，切向内力产生的应力刚化效应显著抑制了偏心旋转的不稳定。

图9(a)描述了在考虑切向内力的情形下，偏心距与中性圆半径配比和公转转速对不稳定域的影响。为便于描述，将不稳定参数域按上述配比分为两部分，如图9(b)中的①和②所示。其中，参数域①的偏心距小于等于中性圆半径，参数域②表示其余部分。在参数域①中，不稳定域的分布特点与图7(d)一致，稳定性随偏心距的减小、公转转速的增大而提高，以图9(c)最为明显。在参数域②中，高公转转速范围内出现了陡增的不稳定域，以图9(d)最为明显。结合式(22)可知，此时支反力对切向内力的影响更显著。