基于离散元模拟的巨厚煤层分层开采覆岩裂隙演化分形特征*
2021-09-19陈砺锋刘智奇
陈 凯 葛 颖② 张 全 陈砺锋 刘智奇
(①新疆大学, 乌鲁木齐 830046, 中国) (②香港理工大学, 香港 999077, 中国)
0 引 言
新疆煤炭资源丰富,预测煤炭资源储量居全国首位,是构建“丝绸之路经济带”能源战略的核心区域,同时也是我国21世纪十分重要的能源基地接替区和战略能源储备区。然而,西部矿区的煤炭开采条件、水文地质工程地质结构特征与东部煤田存在较大差异性,且煤炭资源具有开采厚度大的特点。随着“一带一路”倡议的不断推进,西部矿区以后将普遍面临巨厚煤层在分层采动作用下覆岩裂隙发育特征如何演化的问题。
《中国煤田地质学》将单层厚度为8m以上的煤层划分为巨厚煤层(杨起等, 1979)。目前,大采高综采技术可采煤层厚度可达7~8m(朱涛, 2010),综放技术可采煤层厚度已可达20m左右(康天合等, 2007),还有部分文献将单层煤厚度超过40m或60m的称为巨厚煤层(胡社荣等, 2011)。本文从煤炭地下开采角度出发,并结合当前开采技术条件,将我国采用综放开采方法一次采出煤层最大厚度为20m左右的称为巨厚煤层(许猛堂, 2014)。
采动覆岩裂隙的发育特征和演化规律对评价矿山突水溃砂灾害的发生具有重要意义(隋旺华, 1994;隋旺华等, 2019)。近年来,国内外相关专家和学者在“上三带”理论和“关键层”理论的基础上(刘天泉, 1995; 钱鸣高等, 1996),对特厚和巨厚煤层采动下覆岩的工程地质问题开展了大量的研究工作。乔小龙(2017)采用分段注水、钻孔电视、地质雷达、微震监测探测研究了大采高综放开采覆岩破坏特征,并对传统经验公式进行了修正; 张宏伟等(2014)采用EH-4大地电磁法对复杂巨厚煤层综放开采覆岩破坏高度进行了深入研究,并通过采用理论计算和数值模拟方法对探测结果进行了验证; 韩军等(2016)采用数值计算、微震监测和瞬变电磁探测方法对巨厚煤层软弱覆岩分层综放开采条件下覆岩破坏特征进行了分析,确定了采出厚度与覆岩破坏高度的关系; 田成东(2016)针对巨厚煤层开采后覆岩移动及地表下沉规律与一般厚度煤层相比具有很大差异性的特点,综合运用现场踏勘、关键层理论、相似材料试验和数值模拟等方法,对鄂尔多斯地区巨厚煤层开采覆岩移动及地表下沉特征进行了系统研究; 王金华(2013)研究了塔山煤矿特厚煤层大采高综放工作面顶煤顶板运移规律,成功研发了大采高综放工作面片帮综合防治技术; 任启寒等(2021)针对特厚煤层综放采场开采条件,对采场围岩应力演化规律、覆岩结构特征及矿压显现规律进行分析。
新疆巨厚煤层资源赋存丰富,面对巨厚煤层在高强度、大规模开采时对上覆基岩结构的破坏和地表生态环境的影响的问题,部分专家和学者开展了新疆矿区巨厚煤层覆岩破坏的相关研究工作。曾强等(2019)基于准东大井矿区赋岩柱状及岩性,构建了赋岩物理模型与数值模型,开展了覆岩位移与含水层渗透特性的模拟研究; 李根生等(2018)针对准东矿区巨厚煤层典型赋存特征,通过识别覆岩关键层及含水层,采用UDEC数值模拟方法,对不同开采方法覆岩含水层破坏进行了模拟研究; 秦冬冬(2020)围绕准东矿区巨厚煤层分层开采覆岩结构演变及采场矿压控制展开了系统研究,提出了以分层采厚和失稳岩层碎胀系数为关键参数的“梁式结构、高位梁式结构或应力拱结构”顶板承载结构形态判别方法; 管伟明(2018)阐明了准东大井矿区巨厚煤层累积采厚、分层采厚对覆岩破断特征及结构演变过程的影响规律。
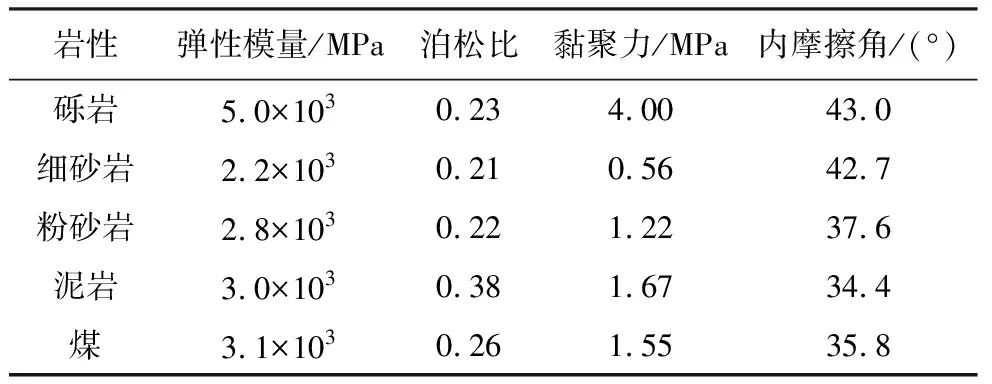
表 1 煤岩层力学参数表Table 1 Mechanical parameters of coal and rock strata
因此,随着新疆地区煤炭资源开发强度的不断增大,为了保证矿井的安全开采和水资源的保护,需要对高强度开采条件下巨厚煤层覆岩裂隙网络进行定量评价。而分形几何理论是定量评价采动覆岩裂隙场发育特征的一种非线性数学方法,在实际工程中也得到了较好的应用(李振华等, 2010)。虽然在已有研究成果中也有对采动覆岩裂隙分形演化规律的研究,其研究内容主要针对薄煤层或者薄基岩,而对巨厚煤层在分层开采作用下覆岩裂隙分形演化规律的研究则相对较少。因此,本文针对乌鲁木齐县白土窑煤矿典型的煤炭赋存条件和水文地质结构特征,通过数值模拟和分形几何理论相结合的方法对巨厚煤层在分层开采条件下覆岩裂隙场的发育特征和演化规律进行定量评价,进而为西部矿区巨厚煤层的安全开采和水资源的保护提供科学依据和技术参考。
1 研究区工作面概况
白土窑煤矿隶属新疆昌平矿业有限责任公司,是由原白土窑煤矿、西山农牧场、浅水河煤矿整合而成的大中型煤矿。1101工作面位于整合后的白土窑煤矿中部靠近南侧B1煤层露头带,为该矿首采工作面,设计走向长度1000m,倾斜长度154m,采用综采放顶煤采煤方法。地层走向近南西—北东向,倾向北西,主采煤层为B1煤,倾角约22°,厚度17~23.5m,接近露头带煤层厚度最大,属于典型的西部矿区高强度开采煤层。
研究区B1煤层顶板以泥岩为主,局部为泥质粉砂岩,泥质胶结,岩石质量总体上属极劣-中等,岩体破碎-中等完整,软化系数在0.03~0.40之间,平均值为0.26,岩石遇水极易软化,抗水性差,属极软-较软岩。此外,研究区B1煤层直接底板大多为黏土岩(黏土矿),从0到几米不等,间接底板为泥岩、细砂岩,岩石软化系数在0.16~0.65之间,平均值为0.35,岩石遇水极易软化,抗水性差,属极软-较软岩。
研究区位于天山北麓地下水径流区,直接充水含水层为侏罗系中统西山窑组孔隙裂隙承压弱富水含水层,其单位涌水量q为0.0075L·(s·m)-1,预测出+600m水平以上首采区正常涌水量906m3·d-1,最大涌水量1359m3·d-1; 间接充水含水层为新近系上新统独山子组孔隙承压含水层,其单位涌水量q为0.061L·(s·m)-1,该工作面受弱富水的直接充水含水层和与之有联系的间接充水含水层两个含水层影响,采动破坏波及后涌水量大,且由于在孔深198.26~206.90m之间分布有8.64m的流砂层,岩性以岩屑和长石为主,分选中等,磨圆度次圆状。因此,该工作面将会面临在弱富水性含水层下仍发生涌水溃砂的工程地质问题。矿区水文地质剖面如图 1所示。
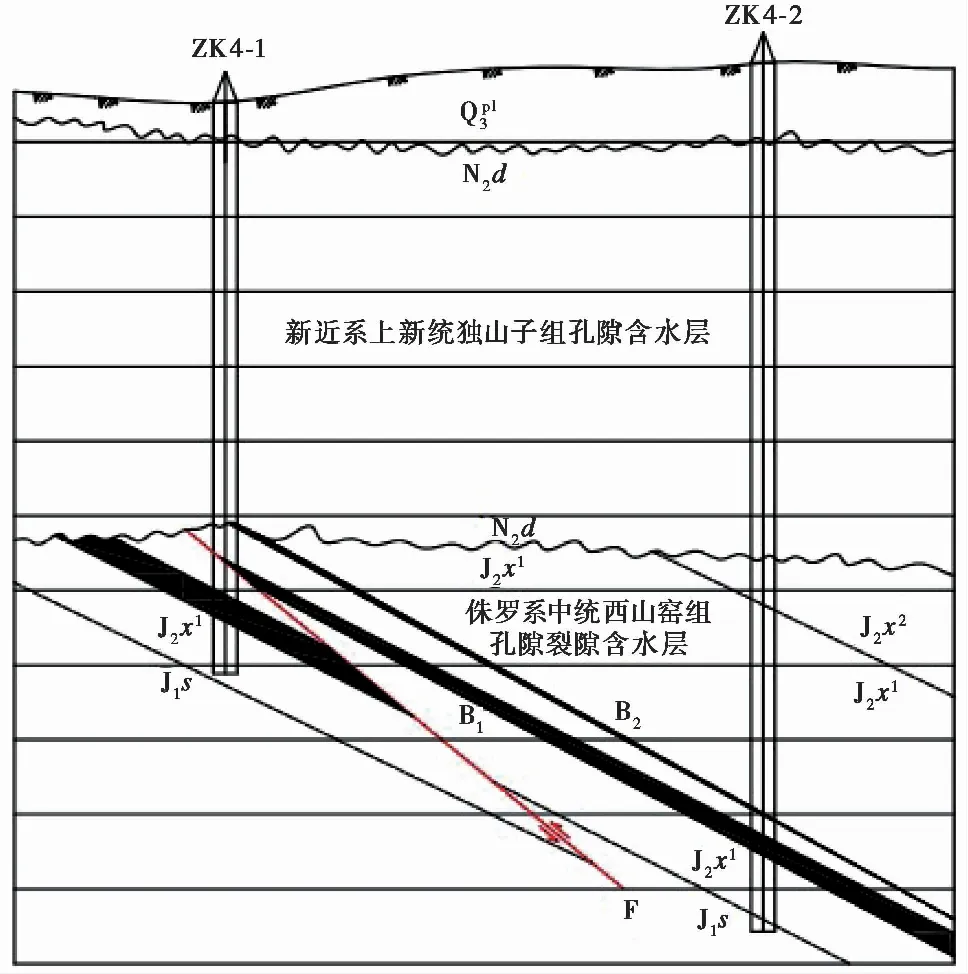
图 1 研究区水文地质剖面图Fig. 1 Hydrogeological profile of the study area
2 采动覆岩裂隙演化研究方法
2.1 离散元数值模拟
离散元数值模拟是获得采动覆岩裂隙演化的方法之一。本文采用UDEC软件对乌鲁木齐白土窑煤矿1101工作面采动覆岩的裂隙演化特征进行数值模拟分析。在对该矿区1101工作面采矿地质条件分析的基础上,建立了长度为600m,高度为297.8m的数值模拟计算模型(图 2),进而可以获得1101工作面采动覆岩裂隙网络的发育特征和分布形态。1101工作面开采结束时覆岩裂隙分布特征如图 3所示。
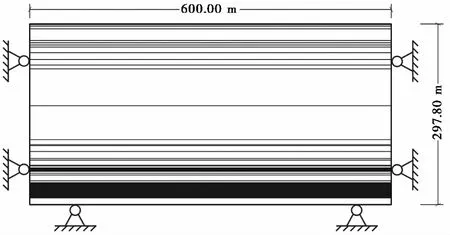
图 2 数值模型简图Fig. 2 Simplified numerical model
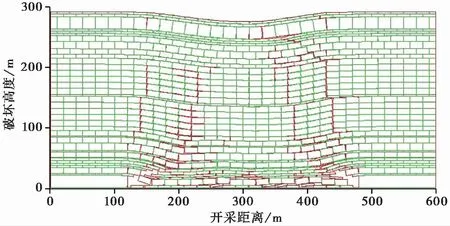
图 3 1101工作面开采结束时覆岩裂隙分布特征Fig. 3 Fracture distribution of overburden in the second layer mining
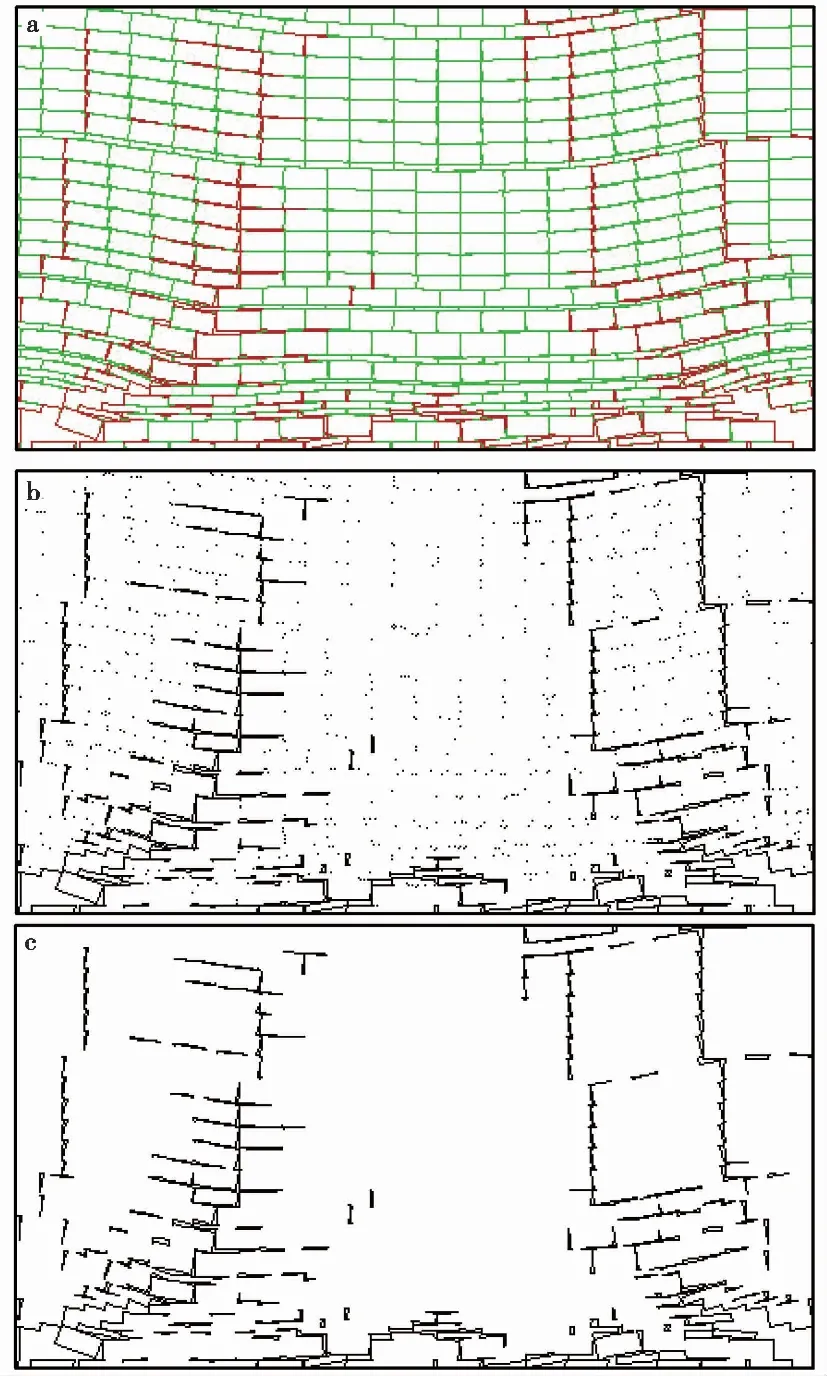
图 4 裂隙发育图像预处理过程Fig. 4 Pre-processing of fissures image a. 裂隙发育图像(部分); b. 黑白位图处理(除噪前); c. 黑白位图处理(除噪后)
该数值模拟计算模型上边界为自由边界,左、右和下边界为固定边界,同时为了减小左、右边界效应,在两侧各留设有120m的煤柱,中间开采长度为360m。数值模拟计算模型中煤岩层本构关系采用莫尔-库仑准则,节理采用节理面接触-库仑滑移准则。各岩层与节理的物理力学参数见表 1。由于煤层厚度为20m,煤层分为两次分层开采,每一分层开采厚度为10m,煤层分层开采开切眼均位于数值模拟计算模型右侧,每次推进距离为12m。
2.2 分形维数的计算
分形维数是分形几何学重要的概念之一。本文采用Fractal Fox 软件对该工作面采动覆岩裂隙网络的分形维数进行计算。Fractal Fox 软件是一款可以在Windows操作系统下利用Matlab语言开发计算分形维数的软件(李水根, 2004),具体采用计盒维数的计算算法。计算步骤主要分为以下3个阶段(彭瑞东等, 2004):
(1)二维数字图像处理前阶段:将选取好的二维数字彩色图像调入Photoshop软件中,如图 4a所示,接着通过阈值分割法设定好一个灰度阈值将裁剪好的计算区域转换为黑白位图,使得转换后的黑白位图中只存在白色和黑色两种颜色,其中黑色区域为采动覆岩裂隙的发育特征和分布形态,而白色区域为未破坏的覆岩(图 4b)。
(2)二维数字黑白位图增益除噪阶段:从图 4b处理好的黑白位图图像中可以看出,除了采动覆岩发育的裂隙呈现黑色外,在其他区域还分布有一些排列杂乱无章的小黑点,但是这些独立的小黑点并不能完全展现裂隙发育的真实情况,因此需要对黑白位图图像进行增益除噪,可以通过Photoshop软件将干扰的小黑点进行消除,达到对黑白位图图像进行增益除噪的目的(图 4c)。
(3)分形维数计算阶段:将经过Photoshop软件处理好的二维数字图像调入Fractal Fox分形计算软件中,采用盒维数算法对其进行分形维数的计算。计算公式如下:
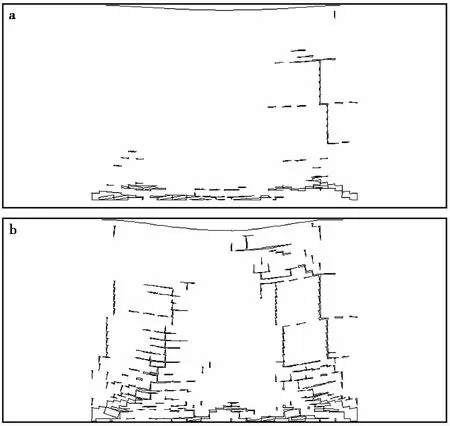
图 5 采动覆岩裂隙发育分布特征Fig. 5 Development and distribution characteristics of cracks in overburden rock caused by mining a. 第1分层开采结束; b. 第2分层开采结束
(1)
式中:r为正方形的边长;N(r)为盒子数;D为采动覆岩裂隙分形维数。
3 采动覆岩裂隙演化的分形规律
3.1 采动覆岩裂隙分形维数的计算
在对巨厚煤层分层开采覆岩裂隙演化离散元计算结果的基础上,通过Photoshop软件对采动覆岩裂隙发育分布特征进行了提取,部分第1分层和第2分层采动覆岩裂隙发育分布如图 5a~5b所示。
通过Fractal Fox 软件对第1分层和第2分层采动覆岩裂隙发育的分形维数进行了计算(表 2),从表 2中可以看出:在第1分层和第2分层开采条件下覆岩的裂隙发育和扩展具有良好的自相似性,分形维数D在0.461~1.488之间,线性相关系数R2在0.617~0.961之间,其线性相关性较好。
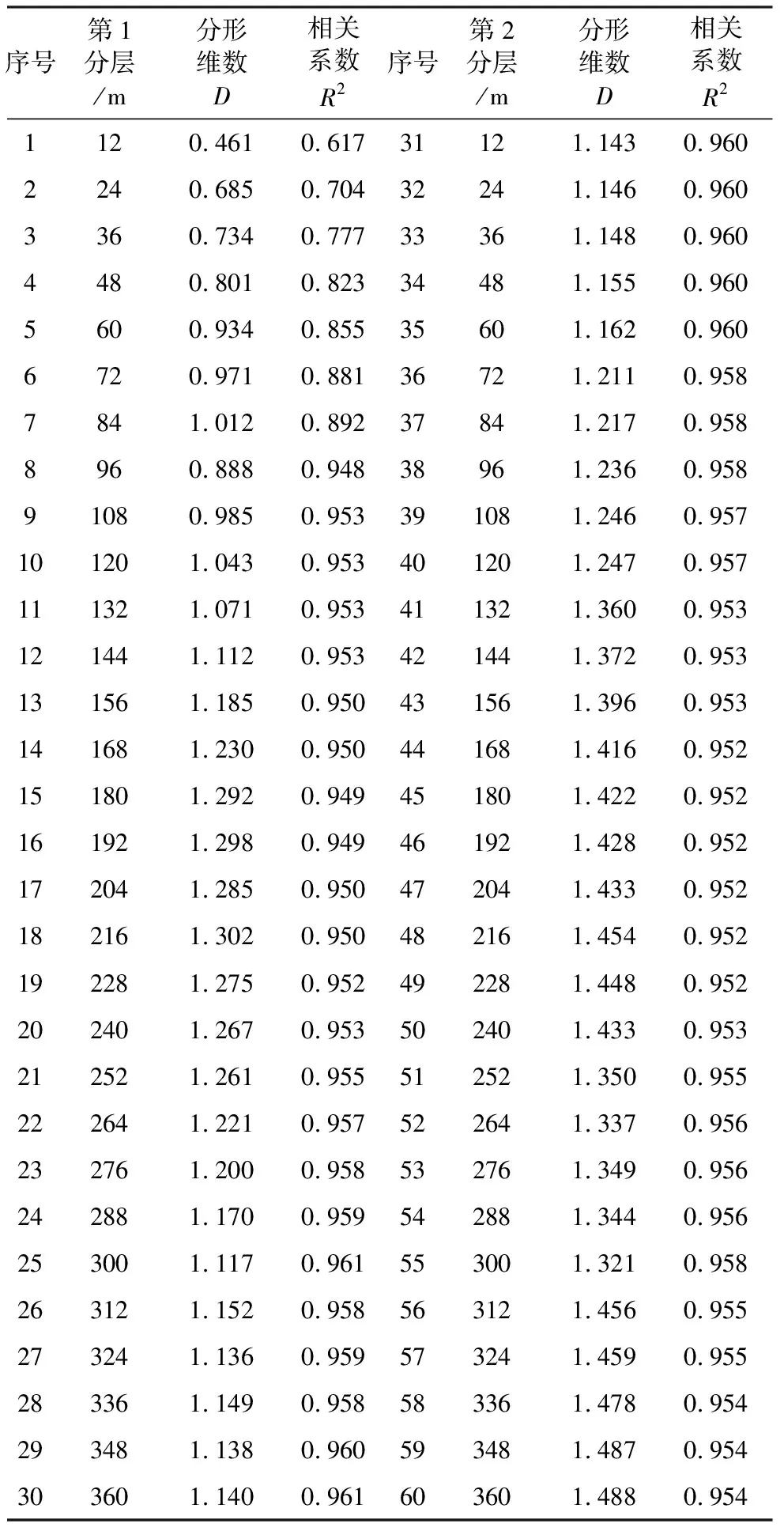
表 2 采动覆岩裂隙的分形维数计算Table 2 Calculation of fractal dimension of cracks in overburden rock cracks caused by mining
3.2 分形维数与开采次数关系
通过表 2可以看出:在巨厚煤层全开采阶段分形维数D在0.461~1.488之间。从图 4a~图4b采动覆岩裂隙发育分布特征可以看出:巨厚煤层开采覆岩裂隙范围主要集中在开切眼两端,且纵向断裂裂隙和横向层间拉张裂隙具有周期性的发育和闭合的特征; 同时,在开采过程中,地表也逐渐出现了地面塌陷地质灾害。因此,该矿区1101工作面既面临要预防直接充水含水层侏罗系中统西山窑组含水层矿井水害的发生,又要实现对新近系上新统独山子组含水层保水开采。
巨厚煤层开采覆岩裂隙的周期性演化过程具有一定的动态性和复杂性,而借助分形维数则可以较好地定量评价其周期性演化的过程。由于煤层厚度是20m,分两次进行开采,所以为了描述全过程开采阶段,采用开采次数N来描述覆岩裂隙分形维数D的演化规律。如图 6为巨厚煤层开采全过程分形维数D与开采次数N的关系曲线。从图中可以看出,在长度为600m,高度为297.8m的研究范围内,随着开采次数N的增加,巨厚煤层开采覆岩裂隙分形裂隙网络的分形维数D总体是增大的趋势,但由于分层开采的影响(0~30次为第1分层开采阶段, 30~60次为第2分层开采阶段),分形维数D在第1分层开采结束前后处于近似稳定状态。通过回归分析可以看出,开采全过程分形维数与开采次数关系呈对数关系,相关系数R2为0.823,其回归公式如下:
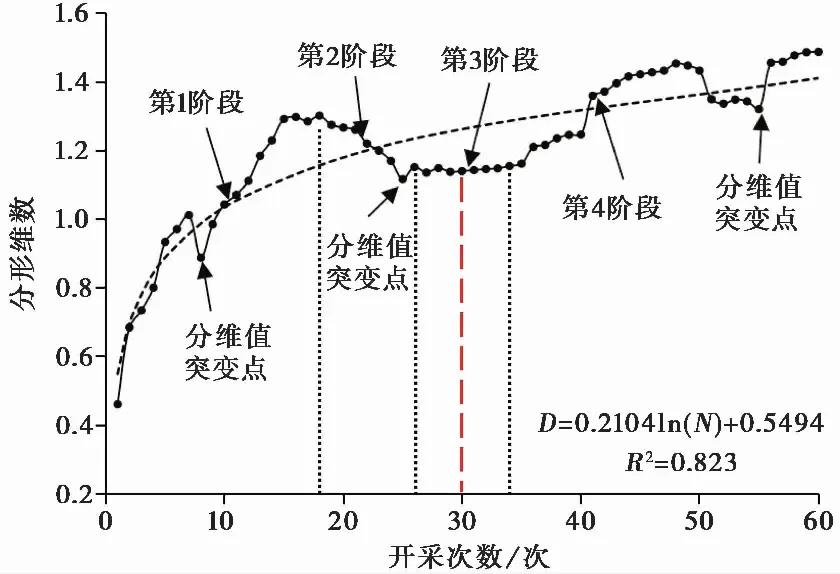
图 6 开采全过程分形维数与开采次数关系曲线Fig. 6 Fractal dimension vs. mining times in whole mining procedure
D=0.2104ln (N)+0.5494
(2)
从表 2和图 6可以看出:在巨厚煤层开采全过程中,采动覆岩裂隙分形维数D的演化规律具体可以分为快速升维阶段、快速降维阶段、平稳稳维阶段、周期性变维阶段等4个阶段。分别如图 7a~图 7d所示。
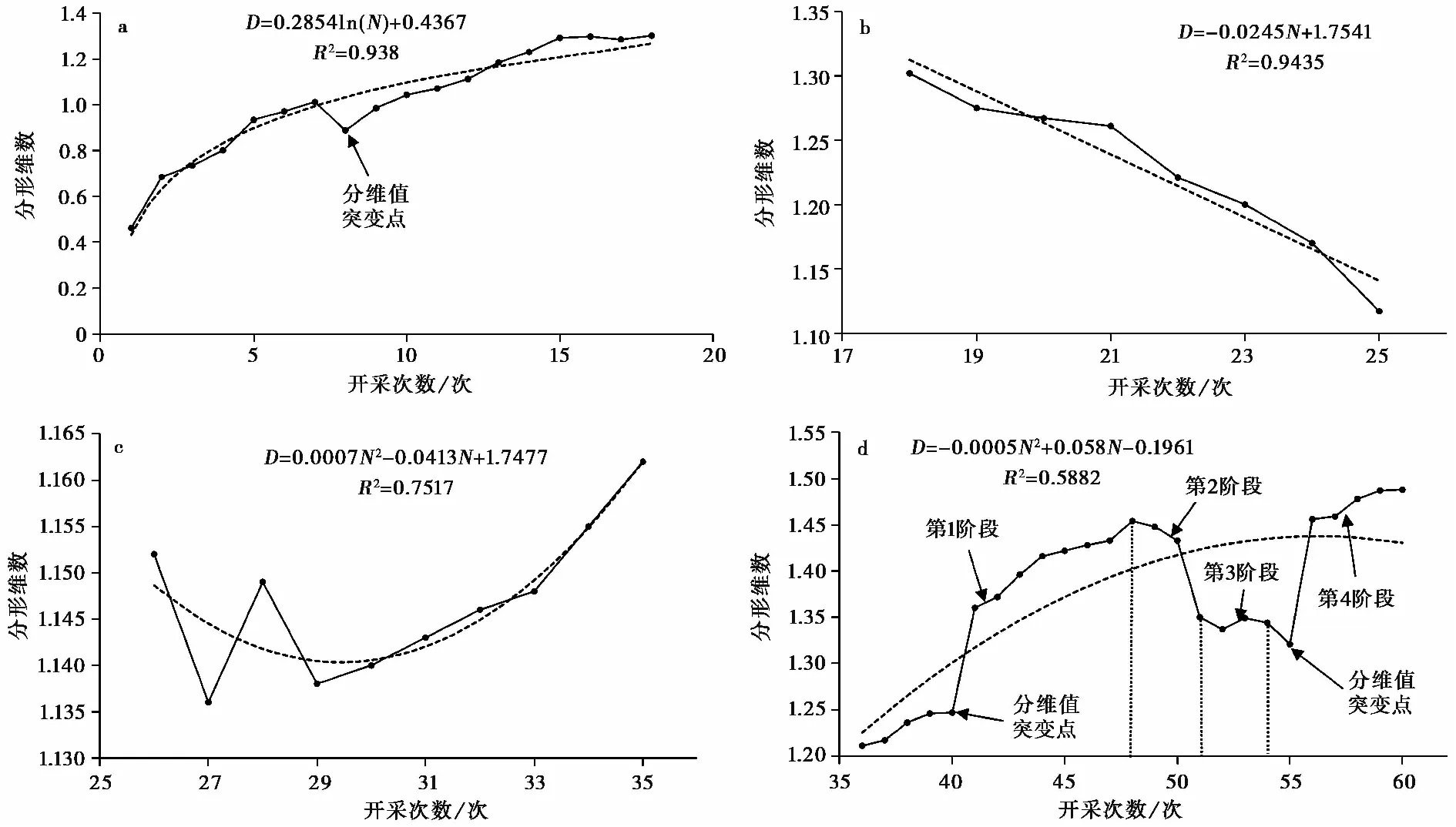
图 7 各阶段分形维数与开采次数曲线Fig. 7 Fitting curves between fractal dimension and mining times in every stage a. 第1阶段; b. 第2阶段; c. 第3阶段; d. 第4阶段
第1阶段:快速升维阶段。该阶段处于第1分层从初始开采到工作面推进至204m,随着开采距离的逐渐增大,覆岩内部竖向断裂裂隙和层间拉张裂隙逐渐发育,当工作面开采距离推进到84~96m覆岩发生初次来压,由于弱胶结覆岩发生剧烈垮塌,使已经发育形成的层间裂隙网络被压实,因此在该段开采距离,其分形维数值出现突变点,从1.012下降到0.888,如图 7a中分维值突变点所示。随后,随着开采距离的不断增大,弱胶结覆岩的裂隙网络也不断形成,其分形维数值也从0.888持续增加到1.302。通过回归分析可以看出,在快速升维阶段内分形维数和开采次数满足对数关系,相关系数R2为0.938,其回归公式如下:
D=0.2854ln (N)+0.4367
(3)
第2阶段:快速降维阶段。该阶段处于第1分层从204m到工作面推进至300m,随着工作面的不断推进,直接顶出现周期性垮落,而工作面也出现连续周期来压现象,由于中间部位裂隙逐渐被压实,致使弱胶结覆岩裂隙网络逐渐减小,其分形维数值也从1.302迅速降低到1.117,如图 7b所示。通过回归分析可以看出,在快速降维阶段内分形维数和开采次数满足线性关系,相关系数R2为0.9435,其回归公式如下:
D=-0.0245N+1.7541
(4)
第3阶段:平稳稳维阶段。该阶段处于第1分层开采结束到第2分层开始阶段,即从第1分层开采距离312m到第2分层开采距离60m。在该阶段弱胶结覆岩裂隙形成-闭合处于一个动态的稳定变化阶段,其分形维数值则稳定在1.152~1.162之间,平均值为1.147,如图 7c所示。通过回归分析可以看出,平稳稳维阶段内分形维数和开采次数满足二次函数关系,相关系数R2为0.7517,其回归公式如下:
D=0.0007N2-0.0413N+1.7477
(5)
第4阶段:周期性变维阶段。该阶段处于第2分层开采距离60m到该分层开采结束。在该阶段内,由于在第1分层开采结束后,裂隙网络的发育已经基本形成,使分形维数值一直维持在较高值。此后,随着第2分层开采距离的不断推进,弱胶结覆岩又开始在原有裂隙网络的基础上形成新的裂隙网络; 但是,由于随着覆岩裂隙网络随着工作面距离的不断推进而呈现出周期性的张开-闭合特征,其分形维数的拟合曲线与第1分层开采阶段表现出了高度的相似性,具有一定的周期性,也会出现分形维数上升阶段-下降阶段-稳定阶段,只是曲线斜率较第1分层开采阶段要缓,如图 7d所示。通过回归分析可以看出,在周期性变维阶段内分形维数和开采次数满足二次函数关系,相关系数R2为0.5882,其回归公式如下:
D=0.0007N2+0.058N-0.1961
(6)
3.3 分形维数与分层开采层数关系
由于西部矿区煤层具有开采厚度大、煤层埋藏浅、地质条件简单、工作面推进速度快等特点,因此,巨厚煤层开采覆岩裂隙网络的演化特征与分层开采层数有一定的关系。如图 8为巨厚煤层第1分层和第2分层开采全过程分形维数D与开采距离L的关系曲线。从图 8中可以看出,随着第1分层和第2分层开采距离L的增加,巨厚煤层开采覆岩裂隙分形裂隙网络的分形维数D总体表现出增大的趋势,但是当煤层开采推进距离达到216m时,由于巨厚煤层开采厚度的影响,覆岩裂隙网络随着工作面距离的不断推进而呈现周期性张开-闭合的特征,致使其分形维数D开始下降。通过回归分析可以看出,第1分层和第2分层开采过程中分形维数D与开采距离L关系均呈幂函数关系,同时也定量印证了弱胶结覆岩裂隙网络随着分层开采次数的增加而呈现周期性张开-闭合的特征,相关系数R2分别为0.7711和0.8139,其回归公式分别如下:
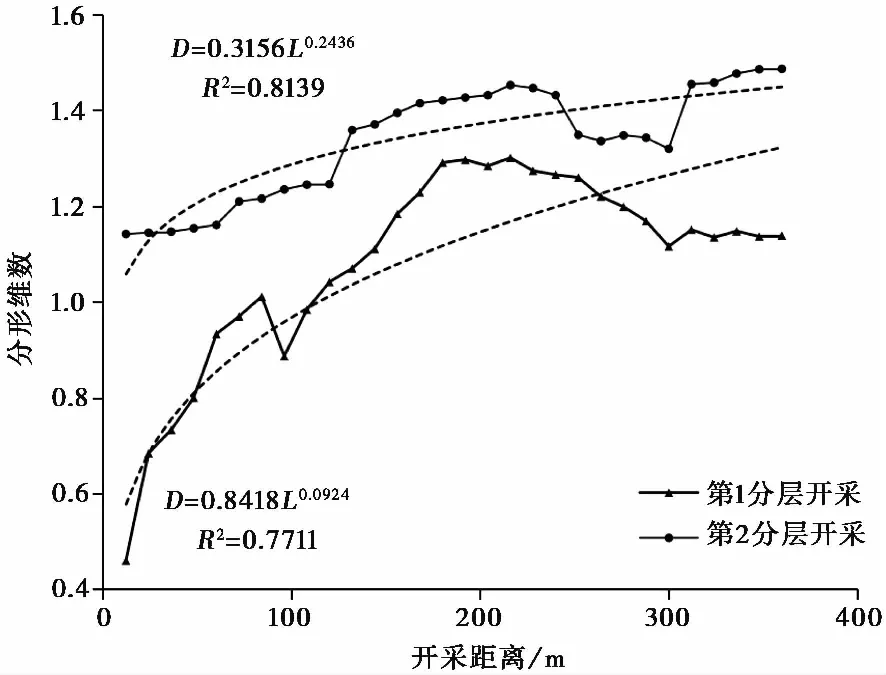
图 8 开采全过程分形维数与开采层数关系曲线Fig. 8 Fitting curves between fractal dimension and number of mining layers in whole mining procedure
D=0.8418L0.0924
(7)
D=0.3156L0.2436
(8)
4 结 论
(1)通过分形理论对巨厚煤层开采全过程采动覆岩裂隙发育的分形维数进行了计算。开采全过程覆岩裂隙的分形维数D在0.461~1.488之间,线性相关系数R2在0.617~0.961之间,其线性相关性较好,表明在高强度开采条件下覆岩裂隙的发育和扩展具有良好的自相似性。
(2)在巨厚煤层开采全过程中,采动覆岩裂隙网络的形成和扩展与分形维数D的演化规律具有一定的相关性,具体可以分为快速升维阶段、快速降维阶段、平稳稳维阶段、周期性变维阶段等4个阶段,各阶段分形维数D与开采次数分别满足对数关系、线性关系以及二次函数关系。
(3)巨厚煤层开采覆岩裂隙网络的演化特征与分层开采层数有一定的关系。弱胶结覆岩裂隙网络随着分层开采次数的不同呈现出周期性的张开-闭合特征,其分形维数的拟合曲线也表现出了高度的相似性; 第1分层和第2分层开采过程中分形维数D与开采距离L关系均呈幂函数关系。
