弯曲角度对油气两相混输弯管冲蚀影响研究
2021-09-17吕广磊
吕广磊
(中海油安全技术服务有限公司,天津 300450)
凝析气井的产物往往呈油气两相混合状态,由于采用两相混输的成本要远低于油气分离后分别运输,因此两相混输管道被广泛的应用于油气长距离运输当中[1]。但采用两相混输将降低管道的寿命,尤其是对于弯管部分。一方面,流动方向的变化,将促使液体油滴与金属管壁频繁接触或附着于壁面之上,从而导致电化学腐蚀的发生[2];另一方面,油滴的输送速度较高,与弯管内壁发生频繁的冲刷碰撞会使材料出现疲劳甚至导致材料的磨损脱落[3]。在腐蚀与冲刷磨损的共同作用下,管道壁面的减薄速率大大提升,增加了管道泄漏失效的风险。
目前,计算流体力学(CFD)方法已经发展的十分成熟,对于相数较少的管流情况,具有十分可靠的计算精度,被广泛应用到两相管流的研究当中[4,5]。孙占炜等[6]通过借助计算流体力学软件Fluent,对三通管内的气液两相流动情况进行了数值分析,发现在三通内会出现油气的初步分离,并得到了支管高度对流型和湍流旋涡的影响规律。李爽等通过实验与计算结合的方法,对上倾管内两相流型和压降进行了研究,分别对高黏度和低黏度情况下的计算误差进行分析,并优化了相关的数值计算模型。Wenlong Jia 等[7]对90°弯管在气液固三相流中的壁面减薄进行了CFD 数值计算,指出磨损是腐蚀与冲蚀共同作用导致的,预测出了壁面主要的减薄区域,并通过实验验证了计算结果。M.Othayq等[8]分析了CFD 中不同的湍流和粒子回弹模型的区别,通过与实验数据进行比对,确定出了最佳的模型组合方案;通过所选模型对气固两相流串联弯管进行数值模拟,从而分析弯管间的距离对颗粒轨迹的影响。
对于油气混输弯管内的冲蚀问题,本文通过CFD方法进行研究,预测一般工况下混输弯管的主要侵蚀部位,分析弯管角度对冲蚀的影响规律,并对其内部的流场结构进行分析讨论以研究其冲蚀机理。所得结果对于油气混输管道系统的安全运行具有一定的指导意义。
1 弯管结构参数与介质流动参数
管道的结构参数(见图1)。选用了油气混输管道的一般管径,即D=200 mm[9];为保证流动的充分发展,提升计算的真实性,弯管前后的管道长度为L=15D=3 000 mm。弯管角度θ 为变量参数,本文中,分别取θ=15°、θ=30°、θ=45°、θ=60°、θ=75°、θ=90°进行研究。
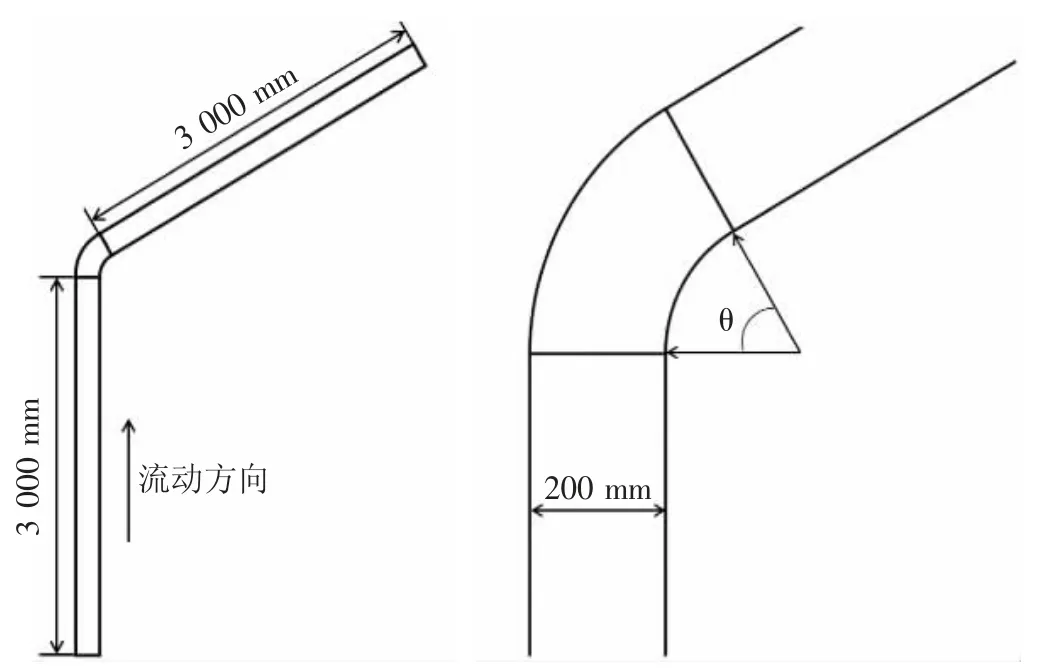
图1 管道结构示意图
本研究采用了CFD-DPM 方法来研究冲蚀过程,气体被看作连续相,由于油相含率较低,且一般呈现为油滴状,故将其看作为离散相来进行计算。其中气相的密度为1.225 kg/m3,黏度为1.798 4×10-5kg·m-1·s-1,油相含率为0.1,油滴密度为860 kg/m3,油气两相的进口速度均为10 m/s。
2 计算模型
本研究应用的CFD 计算模型主要包括:RNG k-ε模型、DPM 模型、General 冲蚀模型、粗糙度模型、随机轨道模型和流固双向耦合等等。其中RNG k-ε 模型计算连续相,DPM 模型计算连续相,General 冲蚀模型计算离散相对壁面的冲蚀,其他的模型用于完善实际工况,提升计算的精确性。设置流体计算域入口为速度入口,出口为压力出口,压力-速度采用SIMPLE 耦合方式,压力离散采用PRESTO 离散格式,其他参数为二阶差分格式,壁面采用无相对滑移边界条件。下面对部分模型进行详细介绍。
2.1 连续相模型
气相被视为连续相,其流量可通过求解雷诺-平均纳维-斯托克斯(RANS)方程[10]得到。该方程可以表示为一个张量:

式中:ρ-流体密度;u-雷诺平均速度分量;p-平均压力;μ-气体黏度;μt-湍流黏度。由于相间相互作用而产生的附加源项由Suip表示。
在求解N-S 方程时,常用双方程的k-ε 模型[11]。与标准的k-ε 模型相比,RNG k-ε 模型可以在多个尺度上捕捉湍流扩散,并考虑壁面附近的涡流和低黏度条件。该模型能较好地处理曲线流动,可以更加精确地求解弯管内的介质流动情况,符合本研究的计算要求。湍动能和耗散方程如下:
离散相模型是基于牛顿第二定律,通过求解作用在粒子上的力的平衡[12]来捕捉粒子轨迹:
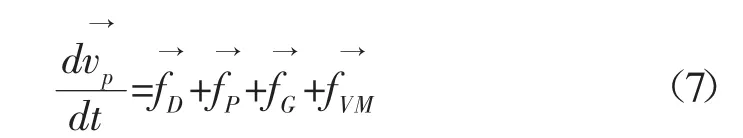
其中:

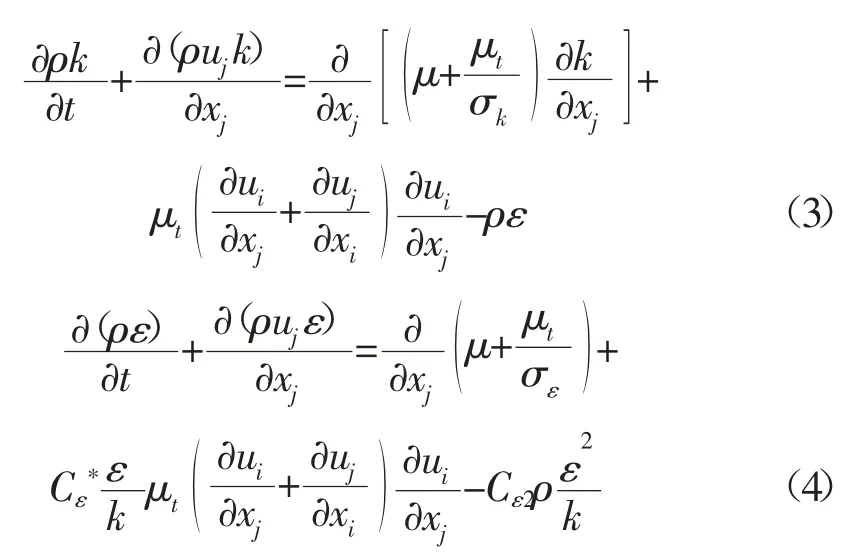
其中:
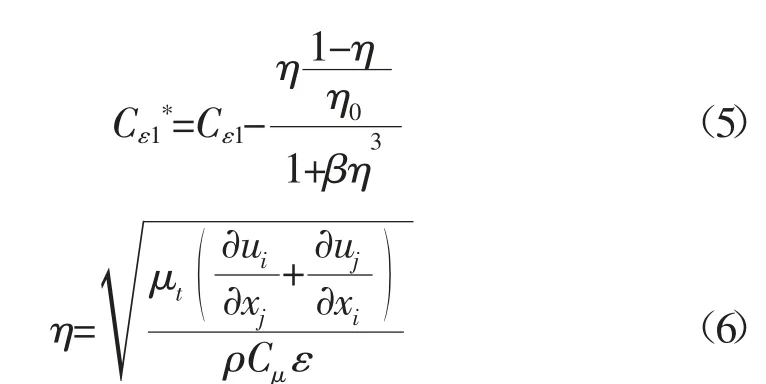
式中:Cε1、Cε2、σk、σe和β 是模型常数。
2.2 离散相模型
2.3 General 冲蚀模型
Fluent 中自带几种冲蚀模型,其中General 冲蚀模型被广泛应用,离散相对壁面的冲蚀速率定义为[13]:

式中:C(dp)-颗粒直径的函数;γ-颗粒的轨迹与壁面的冲击角;f(γ)-冲击角函数;v-颗粒的相对速度;b(v)-颗粒相对速度的函数;Aface-壁面网格面积。
3 网格及其独立性验证
通过ICEM CFD 软件对计算域进行了非结构网格划分(见图2)。为了能更好的捕捉壁面附近的油滴行为和冲蚀分布,划分了8 层边界层网格,所得网格质量均在0.3 以上,满足计算的要求。为了在保证计算精度的同时,尽可能的提升计算效率,故进行网格无关性验证来确定最佳的网格数量。当网格数量达到30 万以上时,最大壁面剪切应力趋于稳定,故确定网格数量在43 万左右。
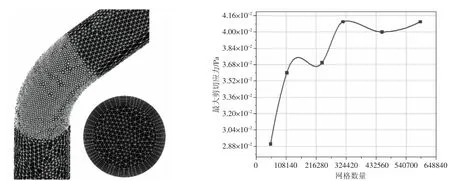
图2 网格与其无关性验证
4 结果与讨论
当弯管角度较小时,冲蚀在弯管与其下游管道上分布广泛,在上游直管段也有少量的点蚀分布,但冲蚀轮廓的形状分散且不规则,最大冲蚀速率一般位于靠近管壁两侧以及网管与直管的过渡区域。随着弯管角度的增大,弯管下游直管上的冲蚀分布缩小,上游直管基本不受冲蚀,冲蚀主要集中发生于弯管附近,且冲蚀轮廓开始呈现为条形,最大冲蚀速率位于弯管顶部(见图3)。
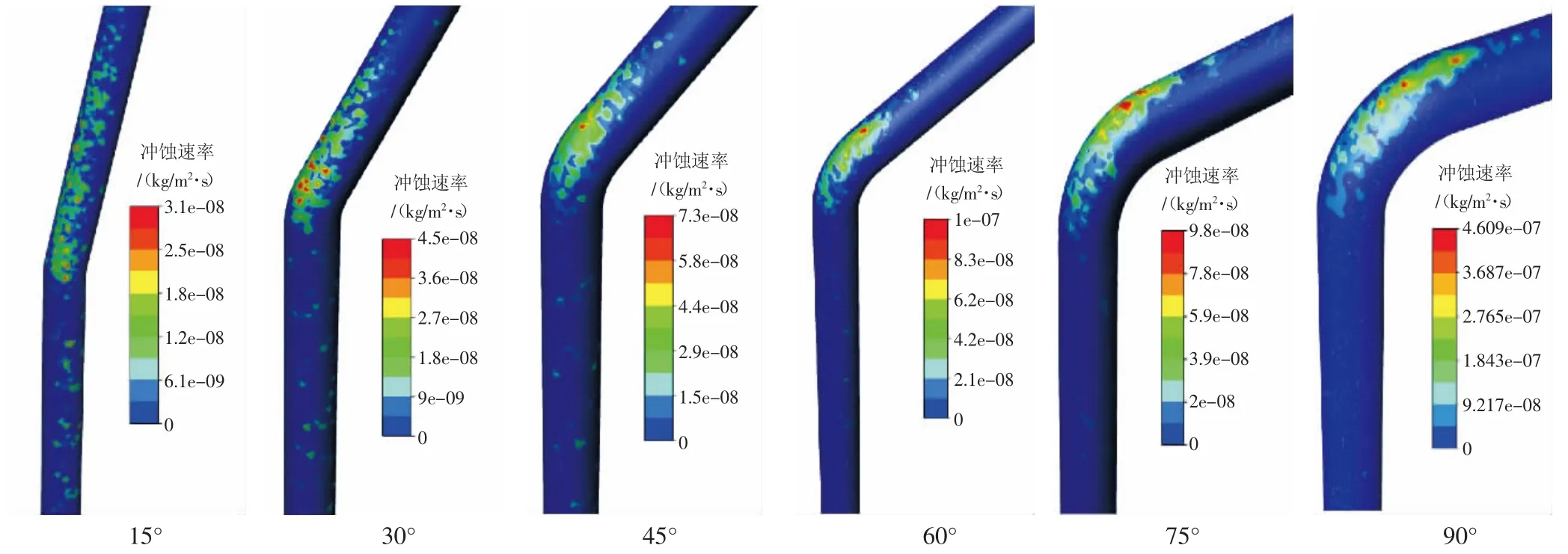
图3 冲蚀云图
最大冲蚀速率是评价管道受冲蚀影响的最关键指标,其大小直接决定了管道的使用寿命;平均冲蚀速率表征管道整体的磨损速率,也是反映冲蚀的重要数据(见图4)。由图4 可知,最大冲蚀速率和平均冲蚀速率均与弯管角度呈正相关,最大冲蚀速率在平均冲蚀速率均在90°时达到最大值,分别为4.609×10-7kg·m-2·s-1和3.37×10-9kg·m-2·s-1。其中,最大冲蚀速率在角度较小时增长缓慢,当弯管角度达到90°,最大冲蚀速率增加幅度显著提升;当角度小于30°时,平均冲蚀速率增长较为平缓,之后呈线性增加趋势。结合以上分析可知,在管道布局情况允许的情况下,适当减小弯管的弯曲角度可以减轻其受到的冲蚀,尤其是对于90°弯管来说,小幅减小角度可以显著提升其抗冲蚀性能。

图4 冲蚀速率随弯管角度的变化规律
为了分析以上规律的原因,深入研究弯管内的冲蚀机理,接下来对各弯管内部的流场结构进行分析。
油滴在弯管内的运动轨迹(见图5),因为与壁面碰撞后的油滴速度会大幅减少,因此根据其速度大小可以判断油滴与管壁的碰撞情况。可以看出,当弯管角度较小时,在下游直管的壁面附近的许多颗粒速度较慢,证明其与下游直管管壁发生碰撞,并且有部分颗粒在管道内发生连续碰撞,从而导致下游直管的冲蚀分布较大,最大冲蚀点也位于其上。当弯管角度增大,低速颗粒分布逐渐向弯管集中,同时在下游直管会出现一明显的无碰撞区域,此时冲蚀主要集中发生于弯管附近,下游直管受到的冲蚀减轻。同时,可看出颗粒的速度随弯管角度的增大而增大,这解释了冲蚀速率随弯管角度增大的现象,特别是当弯管角度为90°时,颗粒速度提升明显,并且此时颗粒的冲击角度将会达到一个危险值,使冲蚀模型中的冲击角函数f(γ)较大,从而使最大冲蚀速率大幅提升[14]。

图5 油滴轨迹
本研究的计算中设置了流固耦合,即考虑连续相与离散相的相间作用,因此气体的分布状态将会明显影响颗粒的运动轨迹。弯管内气体的速度分布情况(见图6),可看出,随着弯管角度的增大,形成了一个由弯管外拱向弯管内拱逐渐增大的径向速度梯度,这主要是由于弯管内侧的流体在离心力作用下开始向外拱迁移并相互挤压,致使外拱附近压力高而内拱附近压力低,同时压力能转化为动能,使外拱流体速度较低,内拱速度较高。该速度梯度的存在,将使颗粒除了沿主流方向流动外,给予其径向和切向速度,从而增加颗粒与管壁的碰撞频率,加剧冲蚀。随着弯管角度的增加,介质流经时所受的离心力也增大,从而使该速度梯度的分布范围逐渐扩大,将更广泛的影响颗粒行为,导致冲蚀的增加。
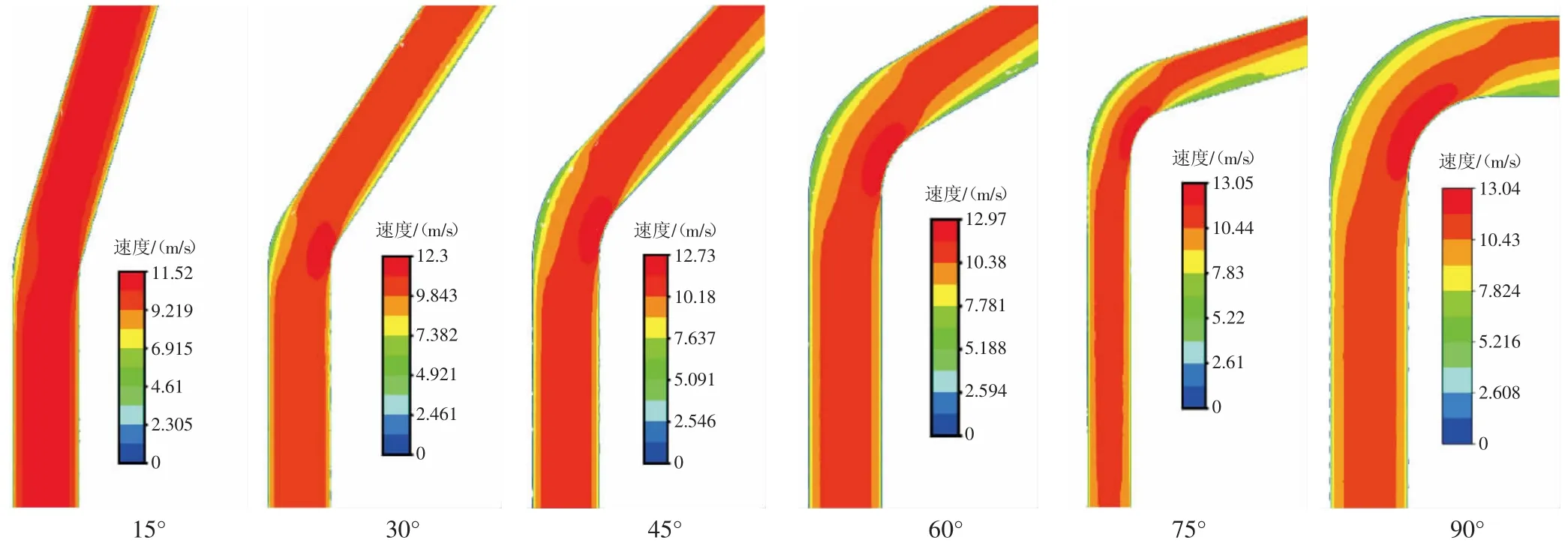
图6 气相速度分布云图
速度梯度的存在将会促进二次流的形成[15],根据以上分析可知,弯管的周向截面上必将存在明显的二次流分布,根据相关研究[16],二次流又将会促进颗粒对壁面的冲蚀,因此对各弯管不同位置截面上的流线进行分析。在弯管进口截面,弯管曲率对其内部流体的影响并不明显,流场稳定,二次流尚未形成(见图7)。在弯管中部,在其曲率的扰动下,湍动效应逐渐增强,两个对称的迪恩涡开始逐渐形成;在弯管出口附近,随着流体逐渐流出弯管,迪恩涡缩小,二次流作用开始减弱。弯管角度增大,对进口截面几乎没有影响,始终没有二次流的产生;但对于中部和出口附近,随着弯管角度增加,迪恩涡的流线愈加密集,湍动能增大,二次流现象更加严重。
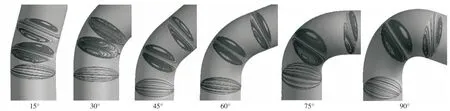
图7 周向截面上的流线图
5 结论
(1)通过网格无关性验证,在该工况下,当网格数量为1053842 时,可以在保证计算精度的情况下尽可能的提升计算效率。
(2)随着弯管角度的增加,冲蚀分布范围逐渐集中,最大冲蚀速率与平均冲蚀速率呈增加趋势,适当的减小弯管角度可以明显提升其抗冲蚀性。
(3)弯管角度会明显影响油滴与管壁之间的碰撞,弯管角度增大会减少油滴与下游直管的碰撞频率,同时使在弯管内部发生碰撞颗粒的冲击角更加易于冲蚀。
(4)在弯管内部离心力的作用下,在周向截面上形成了二次流,且弯管角度越大,二次流越明显。
