多层海洋采气管道上升段屈曲研究
2021-09-17刘子赫郭志阳莫光贵李昌华张学龄
刘子赫,郭志阳,莫光贵,李昌华,张学龄
(长江大学石油工程学院,湖北武汉 430100)
作为海洋工程的“生命线”,海底管道因其高效、经济、便捷等优点被广泛应用于海上油气生产活动的各个环节。随着海洋石油工业发展,开采深度不断增加,几乎所有的管道都面临着触发整体屈曲变形的考验。当管道发生屈曲时,可能会同时引发屈服和塑性变形,极大的影响了海底管道的安全。
早期学者主要集中研究在小坡角、小变形条件下的平直管道整体屈曲的理论。最早的海底管道屈曲理论是Hobbs 等[1]在小坡角假设条件下推导出的,仅限于对屈曲发生时刻平直管道临界轴向力的判断,Taylor等[2]于1986 年建立了单拱缺陷及双拱缺陷的管道整体屈曲解析解,该解析解被认为是初始缺陷管道水平向整体屈曲的经典解;Sriskandarajah 等[3]分析了海底管道水平向整体屈曲受几何初始缺陷的影响规律,并求解了不同初始缺陷下管道整体屈曲的临界轴力;Karampour 等[4]推导了指数型土体约束力模型下海底管道水平向整体屈曲数值解,研究了初始缺陷形状对整体屈曲特征的影响;Miles 等[5]采用小比尺模型试验研究了管道水平向整体屈曲规律,重点研究了整体屈曲形成后的发展规律。受限于早期计算机算力不足,研究围绕海底管道的整体理论设计,对大部分工程问题提供了一定理论设计指导,未能有效应对实践工程。
随计算机发展,学者们更多使用有限元方法对包含有预作用水平管道进行屈曲行为研究。刘羽霄[6-8]使用ANASY 软件研究了初始几何缺陷、管土间摩擦系数、土体屈服位移、管道径厚比、管材刚度等参数对管道水平向屈曲的影响规律;佟光军等[9,10]使用ABAQUS对深水海底水平管道屈曲扩展进行了有限元分析,基于弧长法并考虑Ramberg-Osgood 材料非线性本构关系,模拟了在初始椭圆度缺陷下的系统压溃和屈曲扩展过程;刘秉奇[11]利用Python 参数化批量有限元建模方法,研究了单层管的管道径厚比、钢材等级和材料应变硬化特性对水平屈曲传播压力的影响;王成泽[12,13]利用ABAQUS 软件,采用管土摩擦接触模型通过隐式动力算法分析具有初始缺陷的海底单层水平管道的侧向屈曲特性,以及安装枕木对侧向屈曲的控制作用,分析温度、最大应力与侧向变形幅值之间的关系;张晓等[14,15]使用ANSYS 软件建立了侧向载荷作用下X90 单层水平海底管道局部屈曲有限元数值模型,分析了X90 管道局部非线性屈曲模态及特点,探讨了管道参数及管材性能参数对屈曲临界载荷的影响。现有研究集中在海底的水平管道的屈曲行为,但海上天然气的集输还是要经过管汇向上收集。管道的上升段(立管、J型管)极易因为受力不均导致屈曲发生的屈曲行为也亟需进一步的研究。同时,海底管道在现代海洋管道系统中,有单管、管中管(PIP)和集束等形式管道,其中管中管(PIP)形式管道是最常见的。为保障管道的保温性能与防护性能足够通常采用管中管,即输气内管加保温层和保护层的三层套管结构[16],保温层的作用是为避免输气过程中温度过低,在低温高压条件下形成天然气水合物进而堵塞管道;保护层的作用是防止内部管道受外界机械损伤和海水腐蚀。与现实的多层管道的广泛应用相悖的是,受限于建模难度现有研究中模型多为采用单层管道模型。
本文利用有限元方法建立海洋采气管道上升段(立管与J 型管)的屈曲研究模型,对比理论模型验证了模型的准确性。同时,讨论了单管壁厚、三层管组成、保温层厚度等参数对海洋采气管道上升段的抗屈曲能力的影响。通过数值模拟得到一些具有参考意义的结论。
1 模型描述
1.1 物理模型
目前海洋采气的上升段主要有立管、J 型管两种形式,其管道上升段示意图(见图1、图2)。质量较大的海洋平台通过平台张力腿固定在海床上,而多井采气的海底水平管道经水下管汇汇集到上升段,主要为立管和J 型管,进一步汇集到海上平台集输转运。通常,平台的张力腿为坚固钢-混凝土结构且具有较大的弹性模量,即假设其为刚性约束,进一步简化海上平台端为固定约束。
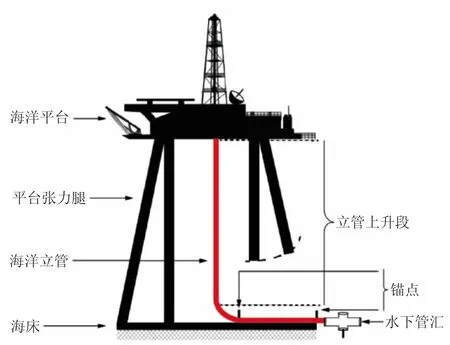
图1 海洋采气管道上升段-立管示意图Fig.1 Schematic diagram of ascending offshore gas pipeline-vertical type
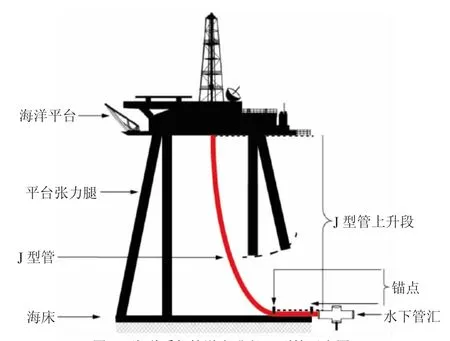
图2 海洋采气管道上升段-J 型管示意图Fig.2 Schematic diagram of ascending offshore gas pipelin-J type
简化的含保温层与保护层采气管道的截面示意图(见图3)。内径为r 的天然气采收管道其厚度为ε1,外部包裹厚度为ε2的保温层,进一步包裹厚度为ε3的保护层,形成一个多层的采气管道上升段截面。

图3 三层管道截面示意图Fig.3 Diagram of three-layer pipeline section
1.2 理论模型
为对比校核有限元模型的准确性,根据美国石油学会标准《API 5L-2018 管线钢管规范》[17]、挪威标准《DNV-OS-FT101:2017 海底管道系统》的基本方法[18],建立了单层采气管道上升段屈曲的理论计算模型。由欧拉公式可知,立管屈曲临界载荷计算公式为:

式中:I-单层管横截面相对于x 轴的惯性矩;μ-单层管的长度因子,根据单层管的约束情况而定;l-单层管长度。
单层管环面的极惯性矩:

单层管横截面相对于x 轴的惯性矩I 为极惯性矩的一半:
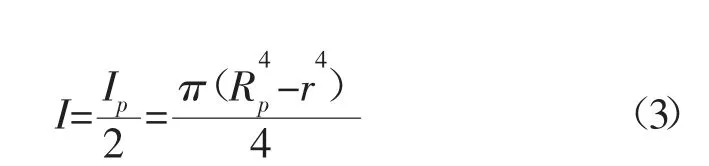
临界载荷为:

公式(4)为单层立管屈曲临界载荷Fcr与立管长度l 变化关系。从式(4)中可以看出,立管屈曲临界压力Fcr大小与立管长度l 成反比,立管长度l 增大,临界屈曲载荷Fcr呈指数减小。
1.3 屈曲问题有限元求解原理
线性化屈曲分析可以用来估计结构失稳发生的临界载荷。一般包含两个步骤,首先使用一较小载荷估算系统的刚度,然后利用特征值分析估算系统的屈曲临界载荷。
受到初始小载荷f 作用,系统的线性响应为:

式中:总的刚度矩阵K 是由线性刚度部分KL和非线性刚度部分KNL组成。
在一阶近似过程中,认为非线性的部分应力是正比于结构的应力,也就是正比于外载荷。结构受到任意初始外载f0时,线性结果为:

进而使用一阶近似为:

进一步等效为系统的特征值问题:
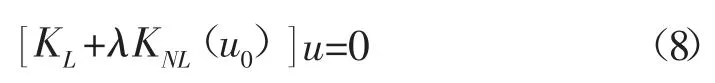
式中:λ-系统特征值,而临界载荷为Fcr=λf0。本研究中利用Abaqus 软件建立了对应采气管道屈曲有限元数值分析模型。
1.4 模型对比
根据《API 5L-2018 管线钢管规范》[17]选择管径为914 mm、壁厚18 mm 的单层立管,弹性模量E=207 GPa,泊松比ν=0.3,屈服强度σ=450 MPa,管道长度l=0.3 m,对比分析数值模型的精度。管道模型采用C3D8R 体单元,网格尺度为0.05 m。管道模型在水面处不考虑平台的影响,将出水界面与海床考虑为刚性界面。理论计算结果为1.21×106kN,而Abaqus 计算结果为1.19×106kN,相对误差1.65%。可知有限元模型与理论结果相差不大,在工程设计允许范围。但理论模型计算仅限于单层均质材料管道的线性屈曲,而限元计算可以分析多层管道复合的屈曲问题。
2 参数分析
为进一步分析管道各相关参数对海洋采气管道上升段屈曲的影响,通过设置单一变量研究各参数的作用。下面研究以某南海海域采气上升段管道为基本参数,管道壁厚ε1=18 mm,保温层厚度ε2=21 mm,保护层厚度ε3=18 mm。管道各层材料说明(见表1)。过去海洋油气资源开采主要集中在500 m 以内的浅水区,近年来随着开采技术进步开采深度不断增加。根据实际情况讨论上升段长度l 为400~800 m 时的临界屈曲载荷。
2.1 管道组成对其抗屈曲能力的影响
2.1.1 单层立管与单层J 型管上升段抗屈曲比较 在海洋管道系统中,随着水深的增加,J 型铺管法的应用优势凸显,被认为是较适合深水海底管道的铺设方式。在数值模拟中J 型管的材料属性与表1 相同,触地点水平管道长度设为100 m。比较结果(见图4)。

表1 管道各层材料性质Tab.1 Material properties of pipeline layers
由图4 可知,J 型管的临界屈曲载荷Fcr同样随管道长度l 的增大而减小,且单层立管的抗屈曲能力要普遍高于单层J 型管,这是因为J 型管道相当于具有初始弯曲的立管,会有较大的抗屈曲能力损失。当上升段长度l=400 m 时,单层J 型管的临界屈曲载荷Fcr=50.16 kN,单层立管临界屈曲载荷Fcr=62.79 kN;当上升段长度l=800 m 时,单层J 型管的临界屈曲载荷Fcr=9.17 kN,单层立管临界屈曲载荷Fcr=15.65 kN。这就是说,按照原有API 或其他标准计算临界屈曲的理论对于J 型管道并不适用,有较大的工程误差。

图4 单层立管与单层J 型管临界屈曲载荷比较Fig.4 Comparison of critical buckling loads between single vertical-type and single J-type pipeline
2.1.2 单层与多层立管上升段抗屈曲比较 单层与三层立管上升段的临界屈曲载荷比较。二者的区别在于输气的管道参数一致,而三层管道外围包裹了对应的保温层和保护层(见图5)。由图5 可知,随开采深度的增加,管道的屈曲临界载荷快速下降,这也和公式(4)结论一致。立管长度l=400 m 时,三层立管的临界屈曲载荷Fcr=117.38 kN,单层立管的临界屈曲载荷Fcr=62.79 kN,抗屈曲能力提高了86.94%;立管长度l=800 m 时,三层立管的临界屈曲载荷Fcr=23.83 kN,单层立管的临界屈曲载荷Fcr=15.65 kN,抗屈曲能力提高了90.61%。三层立管的抗屈曲能力比普通单层立管的抗屈曲能力提升了约一倍,这是因为三层立管的保护层及保温层都有一定抗屈曲能力。具有较为厚实材料的多层立管能够更好预防管道发生屈曲行为,但是同样带来海洋平台负载和成本上的增加。
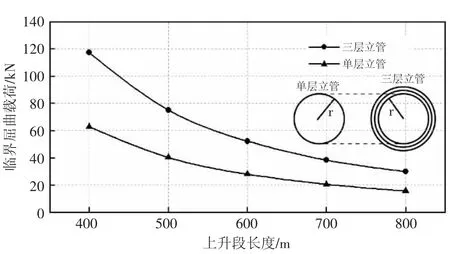
图5 单层与三层立管屈曲临界载荷比较Fig.5 Comparison of critical buckling load between single-layer and three-layers vertical pipeline
2.1.3 单层与多层J 型管道上升段抗屈曲比较 单层与三层J 型管临界屈曲载荷比较(见图6)。当管道长度l=400 m 时,三层J 型管的临界屈曲载荷Fcr=84.78 kN,单层J 型管临界屈曲载荷Fcr=50.16 kN,三层J 型管的抗屈曲能力比单层J 型管的抗屈曲能力提升了68.98%。而其他参数相同的立管,三层管道提升为86.94%,这是由于J 型管自身初始变形引起的抗屈曲能力损失[19]。当管道长度l=800 m 时,三层J 型管的临界屈曲载荷Fcr=23.34 kN,单层J 型管临界屈曲载荷Fcr=9.17 kN,三层J 型管的抗屈曲能力比单层J 型管的抗屈曲能力提升了154.51%。对于采气深度增加,J 型管道受管道长度影响远大于立管,单层立管降低的幅度较大造成多层J 型管抗屈曲能力有较大提升。这就是说在工程上,海洋采气管道采用J 型管的设计时,优先选用较厚实或多层的管道以有效提升抗屈曲能力。
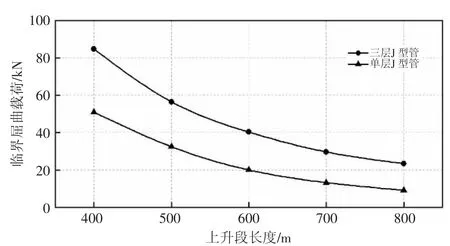
图6 单层与多层J 型管道上升段临界屈曲载荷比较Fig.6 Comparison of critical buckling load between single-layer and three-layers J-type pipeline
2.2 保温层厚度对多层采气管上升段屈曲的影响
为进一步分析保温层的厚度ε2对管道临界屈曲载荷的影响,将保温层厚度分别设置为7 mm,14 mm,21 mm,28 mm,35 mm,获取不同深度的临界屈曲值用以分析。计算中,保护层的厚度均为ε3=12 mm。
2.2.1 保温层厚度对多层立管上升段屈曲影响 不同保温层厚度ε2的立管上升段临界屈曲载荷分析(见图7)。立管长度l=400 m 时,保温层厚度ε2=7 mm 时立管的临界屈曲载荷Fcr=112.61 kN,保温层厚度ε2=14 mm时立管的临界屈曲载荷Fcr=114.99 kN,保温层厚度ε2=21 mm 时立管的临界屈曲载荷Fcr=117.38 kN,保温层厚度ε2=28 mm 时立管的临界屈曲载荷Fcr=119.85 kN,保温层厚度ε2=35 mm 时立管的临界屈曲载荷Fcr=122.41 kN;立管长度l=800 m 时,保温层厚度ε2=7 mm时立管的临界屈曲载荷Fcr=27.89 kN,保温层厚度ε2=14 mm 时立管的临界屈曲载荷Fcr=28.72 kN,保温层厚度ε2=21 mm 时立管的临界屈曲载荷Fcr=29.23 kN,保温层厚度ε2=28 mm 时立管的临界屈曲载荷Fcr=29.80 kN,保温层厚度ε2=35 mm 时立管的临界屈曲载荷Fcr=30.72 kN。立管长度一定时,随管道保温层厚度的增加,临界屈曲载荷有一定的提升。这是因为管道的保温材料的抗屈曲能力有限,未能有效提升管道整体抗屈曲性能。在海洋立管的设计当中,选择合适的保温层厚度与管道长度,用以平衡管道正常输气抗屈曲设计的关系。

图7 不同保温层厚度的立管临界屈曲载荷对比Fig.7 Comparison of critical buckling loads of vertical pipeline with different insulation thickness
2.2.2 保温层厚度对多层J 型管上升段屈曲影响 与立管研究相同,同样的保温层厚度设计放到J 型管模型中进行数值计算。不同保温层厚度ε2对三层J 型管临界屈曲载荷的影响(见图8)。在ABAQUS 有限元计算中,上升段长度l=400 m 时,保温层厚度ε2=7 mm 时三层J 型管的临界屈曲载荷Fcr=76.21 kN,保温层厚度ε2=14 mm 时三层J 型管的临界屈曲载荷Fcr=80.14 kN,保温层厚度ε2=21 mm 时三层J 型管的临界屈曲载荷Fcr=84.78 kN,保温层厚度ε2=28 mm 时三层J 型管的临界屈曲载荷Fcr=87.94 kN,保温层厚度ε2=35 mm 时三层J 型管的临界屈曲载荷Fcr=92.34 kN;上升段长度l=800 m 时,保温层厚度ε2=7 mm 时三层J 型管的临界屈曲载荷Fcr=18.61 kN,保温层厚度ε2=14 mm 时三层J 型管的临界屈曲载荷Fcr=21.97 kN,保温层厚度ε2=21 mm 时三层J 型管的临界屈曲载荷Fcr=23.35 kN,保温层厚度ε2=28 mm 时三层J 型管的临界屈曲载荷Fcr=25.45 kN,保温层厚度ε2=35 mm 时三层J 型管的临界屈曲载荷Fcr=28.42 kN。三层J 型管上升段长度l 一定时,保温层厚度ε2越大,其临界屈曲载荷Fcr越大;保温层厚度ε2一定时,三层J 型管上升段长度l 越大,其临界屈曲载荷越小。在J 型管道的设计当中,既要保证管道的安全性,也要考虑管道的经济性,选择合适的保温层厚度与管道长度,尽可能的防止管道屈曲的发生。
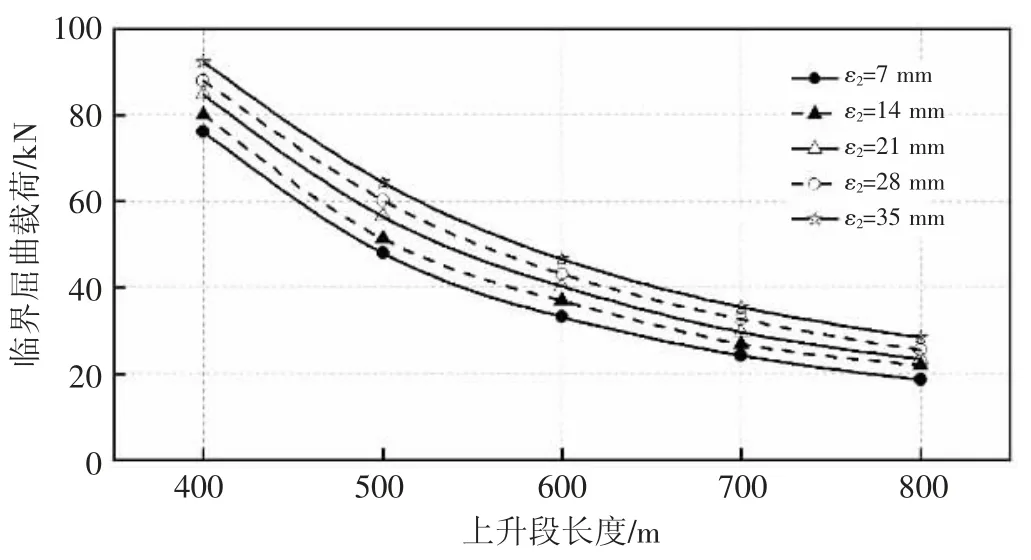
图8 不同保温层厚度的J 型管临界屈曲载荷比较Fig.8 Critical buckling load of J-type pipes with different insulation thickness
3 结论
(1)立管的抗屈曲能力要强于J 型管的抗屈曲能力,管道上升段越长抗屈曲能力越小。
(2)无论是立管还是J 型管,多层管道因为保温层和保护层的存在有一定抗屈曲能力提升。特别是J 型管使用时,多层管道能够有效提升抗屈曲能力。
(3)通过对比研究可得,保温层厚度增加增强抗屈曲能力的同时,也附加制造、安装和维护等各方面的成本,在进一步的研究中将结合经济性分析多层海洋采气管道上升段屈曲行为。
