节段悬臂箱形梁桥拼装施工力学特性研究

王朝阳

（中铁二十一局集团有限公司 陕西西安 710065）

1 前言

德国最先对预制节段拼装技术进行研究，由于其平行施工，间接缩短了施工工期［1－5］。有学者提出了一种新型的异步浇筑施工技术用于解决传统波纹钢腹板梁悬臂施工缺陷问题。Ahmed和Aziz［6］研究预制节段箱形梁桥接缝剪切力学性能。Au和Leung［7］开发出一种在增量荷载或位移下对连续预应力混凝土桥梁进行全程数值分析的技术，用初始刚度法进行迭代，得到一组满足各单元本构模型的容许节点位移和内力。Moon等［8］通过施工顺序分析，研究预制节段梁底板出现的裂缝，发现裂缝是由于在连接节段临时后张拉过程中发生过大变形所致。Kim等［9］研究预应力混凝土梁与预制箱梁拼装阶段的静力学行为。Naser和 Wang［10］研究了节段预应力箱形梁的加固方法，并对其挠度进行现场监测和荷载试验。

综上所述，对于边跨的一半采用支架拼装，另一半采用龙门吊悬臂拼装，最后合龙对接的研究较少。本文利用有限元软件对上部桥梁结构进行深入研究，分析总结节段预应力混凝土箱梁在施工拼装各荷载工况下的力学性能及桥梁结构安全状况，为今后相似工程提供一定的理论依据。

2 悬臂拼装预抛高计算及调整方法

2.1 箱形梁的基本结构

本项目依托郑州东四环上跨七里河南路和上跨商鼎路桥梁工程，其结构主梁主体采用节段预制拼装，中墩和边墩顶0号块采用现浇施工。根据构造及施工架设需要，41～46 m跨径的中跨、边跨均划分14个预制节段，38～40 m跨径的中跨、边跨均划分12个预制节段［11］。悬拼预制拼装节段长度分别为2.9 m和2.4 m，腹板厚度为380 mm，底板厚度为270 mm，如图1所示。墩顶0号块与预制节段间设置15 cm湿接缝，跨中合龙段采用现浇施工。主梁采用单箱单室等高斜腹板预应力混凝土箱梁。顶板设单向横坡，利用箱梁整体旋转形成［12］，3×46 m节段预制拼装连续梁桥是本项目跨度最大的典型桥梁。

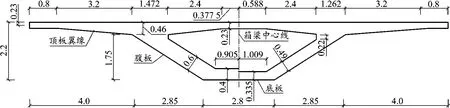
图1 1号和2号块梁体截面（单位：m）

2.2 现浇梁段立模标高计算

（1）立模标高计算公式

立模标高计算公式（以变形向上为正，向下为负）：

式中：H立模为立模标高；H设计为设计标高；f支架为支架的变形；f后期施工影响为后续施工阶段的变形；f后期徐变为竣工后混凝土收缩徐变引起的变形。

竣工标高与设计标高的关系：

式中：H竣工为桥梁竣工标高；H二期恒载为桥梁二期恒载产生的变形。

（2）节段预制拼装箱梁预抛高值

经计算，边跨预抛高值最大值为19.6 mm，中跨预抛高值最大值为2.3 mm，结果如图2～图3所示。

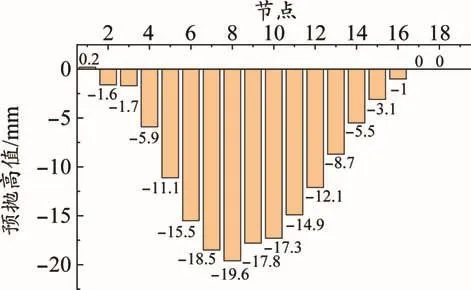
图2 中跨桥梁预抛高值

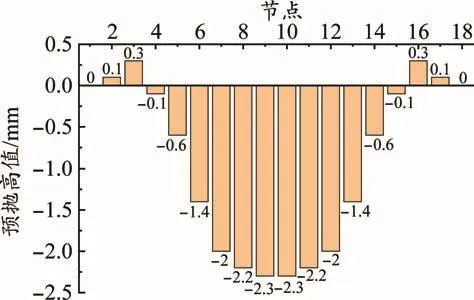
图3 边跨桥梁预抛高值

2.3 预抛高值调整方法

0号块支架现浇箱形梁的预抛高值通过调整立模标高来完成，即在节段箱形梁设计标高的基础上增加预标高值作为立模标高，如图4所示。

图4 0号块箱形梁标高关系

预制拼装梁段预抛高值通过湿接缝调整来完成，即通过调整0号块和1号块梁体间的湿接缝上下开口实现，如图5所示。

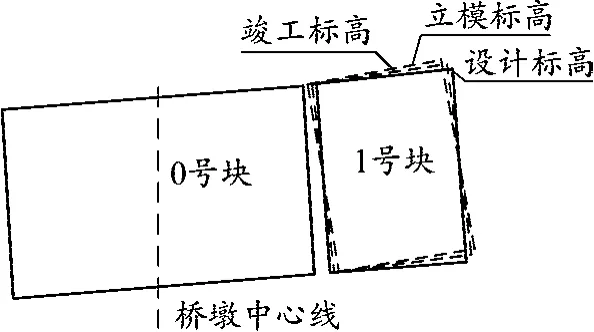
图5 1号块箱形梁标高关系

3 线形控制措施

3.1 控制目标

节段梁体的线形控制取决于预制和拼装两个施工环节，在节段箱形梁悬臂拼装阶段控制要点如下：

（1）“T”型悬臂拼装线形控制必须确保桥墩0号块箱形梁三维坐标的定位精度达到设计值。

（2）边跨支架拼装线形控制用龙门吊将箱形梁段吊至预定位置，精确定位箱形梁的三维坐标，进行线形监测与调整。

（3）在进行节段箱形梁悬臂拼装施工时，由于混凝土材料的特殊性，其弹性模量的计算存在误差，节段箱形梁自重、预制时的线形误差以及预应力张拉等因素对箱形梁的挠度有很大影响，在悬臂拼装时应实时监控并及时调整。

3.2 拼装控制措施

在节段箱形梁理想拼装状态下，无需进行线形调整，临时预应力进行对称张拉，保证节段箱形梁的线形。由于在进行悬臂拼装时会产生较大的线形误差，因此以控制节段箱形梁方向偏转的临时预应力拉杆先张拉为原则。如图6所示，假设顶板N＋2＃箱形梁监测的竖向位置坐标偏低，为了纠正该线形，应当张拉使N＋2＃节段箱形梁上翘的临时预应力，同理，可张拉底板的临时预应力使箱形梁下偏。

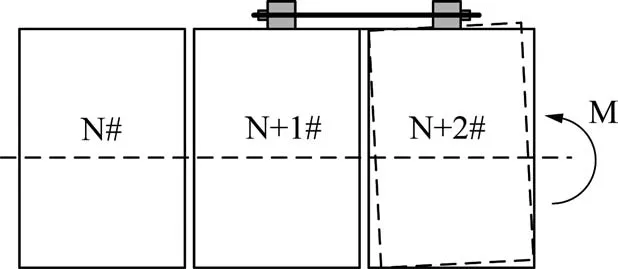
图6 临时预应力施加顺序对线形控制影响

4 拼装悬臂箱形梁施工力学分析

4.1 计算模型

（1）道路等级：城市快速路、主线高架快速路，80 km／h；上部主体结构环境类别为Ⅰ类。

（2）地震作用：根据《建筑抗震设计规范》（GB 50011—2010）（2016 年版）［115］规定地震基本烈度为8度，加速度为0.15 g，场地特征周期为0.55 s，抗震设防类别为乙类。

（3）混凝土：1号～7号块节段预制箱形梁采用C60混凝土，湿接缝；合龙段采用C60自密实细石混凝土。

4.2 节段箱形梁挠度分析

在模拟施工时，墩顶0号块箱形梁浇筑设为工况1，湿接缝与1号块箱形梁施工设为工况2，2号～7块箱形梁拼装设为工况3～工况7，合龙段浇筑设为工况8。

（1）工况1～工况8主梁挠度

支架拼装近边墩一侧箱形梁，龙门吊悬臂拼装中墩“T”型节段箱梁。1～8工况下拼装挠度如图7所示。

图7 1～8工况竖直方向拼装挠度

在1～8工况施工阶段，“T”型拼装竖直方向的最大挠度为45.308 mm，最大挠度出现在工况8梁端部位；边跨中半段梁体采用支架进行拼装，竖直方向的最大挠度为21.60 mm，最大挠度同样出现在工况8梁端部位。可见，随着拼装梁段数量不断增加，梁端挠度值随之增大。

（2）合龙段及桥面二期挠度

如图8所示，对比分析合龙段挠度与桥面二期挠度，可以看出两种工况下挠度变化总体趋于一致，竖直方向的最大挠度出现在边跨与中跨的跨中，合龙段工况下的最大挠度值为30.980 mm，桥面二期最大挠度值为38.020 mm。

图8 合龙段及桥面二期挠度

4.3 弯矩及剪力分析

随着施工进行，每个阶段的梁体弯矩均产生显著变化，弯矩值不断变大，“T”型拼装节段箱形梁最大值弯矩出现在中墩箱形梁截面的顶部；在进行边跨支架拼装节段箱形梁时，最大正弯矩值出现在拼装箱形梁端部，最大负弯矩值出现在梁底部。对整个施工过程进行模拟计算，得到主梁结构拼装时产生的弯矩值。

（1）工况1～工况7弯矩分析

主梁结构拼装时弯矩计算结果如表1和表2所示。

表1 工况1～工况7下支架拼装主梁弯矩M1 kN·m

表2 工况1～工况7下“T”型拼装主梁弯矩M2 kN·m

由表1可知，边跨在进行支架拼装时，最大正向弯矩值为8 678.30 kN·m，最大负向弯矩值－5 590.5 kN·m。由表 2 可知，在进行“T”型拼装时，最大弯矩值不断增加，最大正向弯矩值为49 514.0 kN·m，最大负向弯矩值为－152.81 kN·m。

（2）工况1～工况7下剪力分析

“T”型拼装和边跨支架拼装时的剪力最大值计算结果如表3和表4所示。

表3 工况1～工况7支架拼装主梁剪力f1 kN

表4 工况1～工况7下“T”型拼装主梁剪力f2 kN

由表3可知，边跨在进行支架拼装时，最大正向剪力为2 497.90 kN，最大负向剪力－2 186.8 kN。由表4可知，在进行“T”型拼装时，最大正向剪力为5 005.30 kN，最大负向剪力为－300.2 kN，最大负向剪力的变化较为稳定。

（3）最大悬臂状态施工力学分析

中跨和边跨在7号块拼装结束后剪力和弯矩计算结果如图9所示。

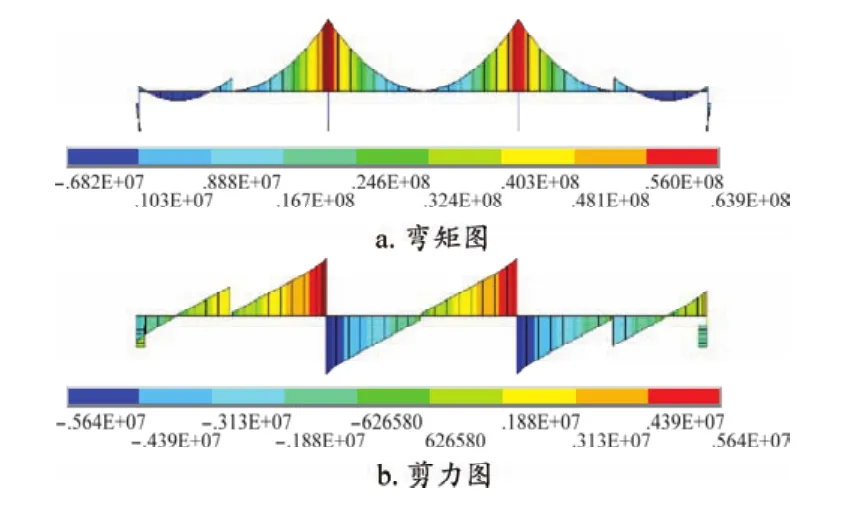
图9 最大悬臂状态内力分布

由图9可知，龙门吊拼装产生的最大弯矩值为63 852.0 kN·m，因此在拼装7号块梁体时，应当在6号块梁体处采取临时支撑措施，以减小悬臂拼装时梁体的弯矩。

5 结论

（1）本桥施工工艺包含节段悬臂拼装、节段支架拼装和支架现浇三种，通过对中跨和边跨抛高值进行理论计算，得出边跨的预抛高最大值为19.6 mm，中跨的预抛高最大值为2.3 mm。线形调整方面，0号块支架现浇箱形梁的预抛高值通过调整立模标高实现，预制拼装梁段预抛高值通过湿接缝调整实现。

（2）通过数值模拟表明：随着拼装梁段数量不断增加，其梁端挠度值不断增大，竖直方向最大挠度为45.30 mm。

（3）在进行“T”型拼装时，正弯矩和剪力对梁体影响最大；而边跨在进行支架拼装时，正负弯矩和剪力会同时对梁体产生较大影响。因此在拼装7号块梁体时，应当在6号块梁体采取临时支撑措施，以减小悬臂拼装时梁体的弯矩。