四阶精度差分法解定态薛定谔方程
2021-09-16刘展源关成波吕英波丛伟艳
刘展源,关成波,吕英波,张 鹏,丛伟艳
(山东大学(威海) 空间科学与物理学院,山东 威海 264209)
在经典物理场方程的数值求解中,差分法是一种最普遍采用的方法[1-3].通过自变量的离散化,差分法把微分方程转化成代数方程,其中最重要的是将待求函数的导数用有限差分近似表示.文献中,各类精度差分公式的推导一般是利用待定系数法,结合泰勒级数转化成线性代数方程组的求解.本文介绍一种更简洁的方法,利用多项式插值导出差分公式,包括二阶精度和四阶精度差分公式.这种方法既易于理解也方便推广到更高的维数和精度.
差分法也经常被应用于定态薛定谔方程的求解,例如一维方势阱、抛物势阱、W形势阱以及各类量子阱和量子点等物理问题的研究[4-17].对于能量分立的束缚态,差分法将定态方程转化成矩阵的本征方程,进而求出能量和波函数的数值解.在上述研究定态问题的文献中,普遍采用的差分公式是3点中心差分公式,其误差为步长的二次方量级,无法满足高精度要求.本文采用四阶精度的差分公式,求解几个经典势场中的定态方程.以一维谐振子为例,我们利用不同精度的差分公式分别计算能级,所得结果表明,四阶精度差分比二阶精度差分收敛更快并且误差更小.此外,我们还讨论了两类有限深势阱,方势阱和抛物势阱,计算了不同势阱深度下的基态能量和波函数,绘出了两个势阱的基态能量和势阱深度的关系曲线.
1 插值法推导差分公式
假设待求函数f(x) 在区间 [a,b] 上是光滑的,取步长h将区间N等分,我们就可以将自变量离散化为一组等间距的节点 {xi=a+i×h;i=0,1,…,N}.数值求解微分方程就是计算出所有节点处的函数值f(xi),而前提是将方程中的导数用有限差分近似表示.在本节中,我们利用多项式插值法推导出一阶导数和二阶导数的差分公式.
1.1 二阶精度差分公式
如图1所示,我们选取xi及其最近邻的两个节点做3点插值,可得二次多项式.
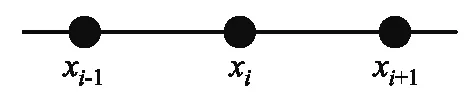
图1 3点插值
利用拉格朗日插值公式[1,3]可以直接写出这个多项式:
(1)

(2)
(3)
这两个式子就是常用的3点中心差分公式,其精度可以结合泰勒级数来分析.将f(xi±1)=f(xi±h) 展开成泰勒级数:
(4)
再代入到中心差分公式(2)和(3)的右侧,可得
(5)
(6)
可见,两个中心差分公式的精度为2阶,其截断误差为步长的二次方量级O(h2).
1.2 四阶精度差分公式
如图2所示,我们取xi及相邻节点做5点插值,可得4次多项式.

图2 5点插值
其拉格朗日插值公式如下
p4(x)=
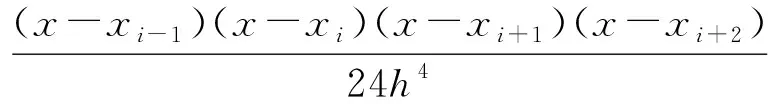
(7)
(8)
(9)
将f(xi±2)=f(xi±2h) 展开成泰勒级数:
其他应收、应付款业务是指电力企业在主营收付款业务之外发生的其他各类往来款项,包括日常供电应收的违约金罚款、对外出租包装物等的租金、收取的职工垫付款、其他各类为政府部门等的垫付款等。根据会计核算规则,需要设置“其他应收款”“备用金”等科目。
(10)
再与f(xi±1) 的泰勒级数式(4)一起代入到5点差分公式(8)和(9)的右侧,可得
(11)
f(2)(xi)+O(h4)
(12)
可见,5点差分公式(8)和(9)的精度比前面的3点中心差分(2)和(3)高了两个阶次.我们如果利用这两个四阶精度的差分公式求解微分方程,原则上可以将计算误差控制在更小的量级.
2 差分法求解定态方程
差分法可以将定态薛定谔方程转化成实对称矩阵的本征方程,而求解线性代数方程有经典的算法和软件(例如MATLAB).本节第1部分以一维谐振子为例说明差分法的应用,利用二阶精度和四阶精度差分公式做计算并对比其结果.在第2部分,我们利用四阶精度差分公式计算有限深方势阱和有限深抛物势阱的基态能量和波函数.
2.1 一维谐振子
一维谐振子的定态方程一般写成如下形式:
(13)
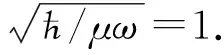
(14)
谐振子的定态都是束缚态,位置概率分布集中在原点的附近.对于能级不是很高的态,可以在有限区间 [-L,L] 内求解方程,并设定边界条件:
ψ(x)=0,|x|≥L
(15)
选取步长h将区间N等分,我们得到一组节点 {xi=-L+i×h;i=0,1,…,N}.考察节点xi处的定态方程,并将波函数的二阶导数用差分公式近似,于是得到定态方程的差分格式:
(16)
也可以写成矩阵的形式:
AΨ=EΨ
(17)
(18)
表示波函数在内部节点处的值;A为 (N-1)×(N-1) 维的实对称矩阵,其矩阵元Aij与二阶导数差分公式相关:
1) 如果选取二阶精度差分公式(3),则有
(19)
2) 如果选取四阶精度差分公式(9),则有
(20)
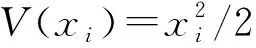
取区间上限L=10,对不同精度的差分公式给出的A矩阵 (19)和(20),我们分别求解其本征方程(17),列出前十个能级的数值结果,并与真值En=n+1/2 对比.
如表1所示,相同步长下得到的计算结果,四阶精度差分明显优于二阶精度的中心差分.特别地,四阶精度差分在步长为0.1时的计算结果已经非常接近于中心差分在步长为0.01时的计算结果,说明前者比后者收敛更快.
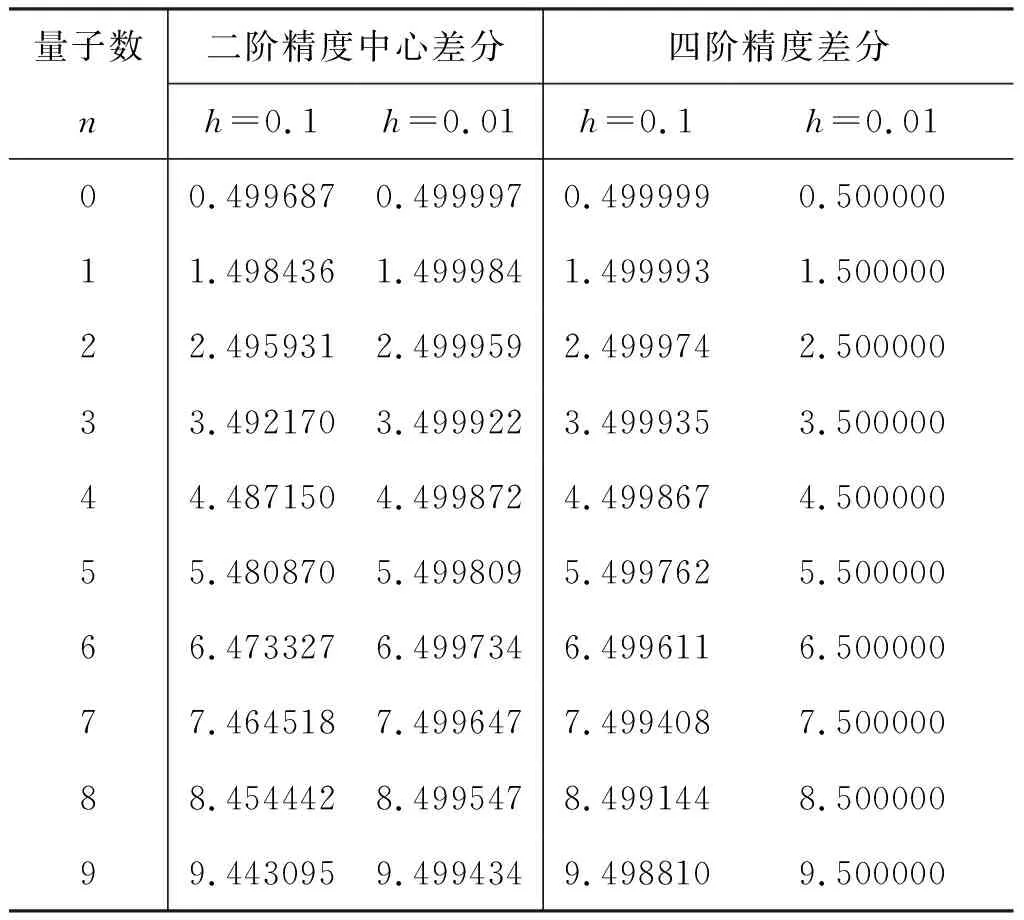
表1 一维谐振子的能级(小数最后一位四舍五入)
2.2 一维有限深势阱
设一个质量为μ的粒子在宽为a深为V0的一维有限深势阱中运动.为了数值计算方便,我们仍然选取自然单位,μ=a=ћ=1,此时能量的单位为ε=ћ2/μa2=1.如图3所示.
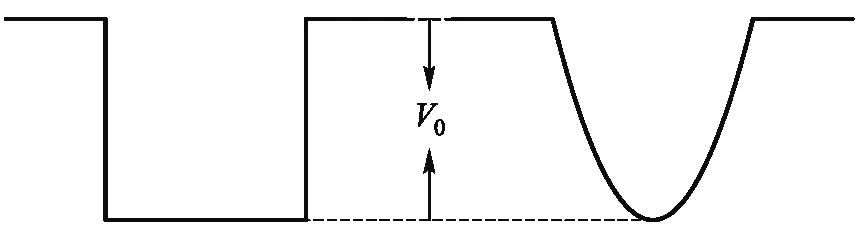
图3 有限深方势阱和有限深抛物势阱
我们讨论两类有限深势阱,方势阱和抛物势阱,对应势函数有如下形式:

(21)
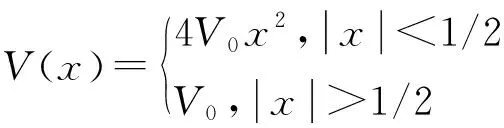
(22)
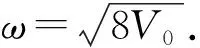
为了数值求解束缚定态,特别是基态,我们取有限区间 [-L,L],以及式(15)中的边界条件.势阱如果不是很深,其束缚粒子的能力较弱,那么基态波函数的分布范围较大,这时L要适当取稍大数值,确保波函数满足边界条件.我们利用四阶精度差分公式分别计算了两类势阱的基态波函数和能量.以下是计算结果及讨论.
图4给出了不同V0时基态粒子的位置概率分布曲线,其中实线表示方势阱中的概率分布,虚线表示抛物势阱中的概率分布.V0取值较小时,粒子在势阱外部的概率分布较大,有显著的隧道效应;V0取较大值时,粒子几乎完全被束缚在势阱内部.另外,对比两类势阱中的概率分布,我们发现,在V0取值0.1和1时,抛物势阱中的概率分布要比方势阱中的概率分布稍宽一些,而在V0取值10和100时却情况相反.原因在于,当V0很大时,势阱内的抛物势斜率也大,从而阻碍粒子向阱壁运动;当V0较小时,抛物势斜率也小,对粒子的运动影响较弱,但抛物势阱相对于方势阱有更大些的基态能量,从而提高了隧道穿透的概率.
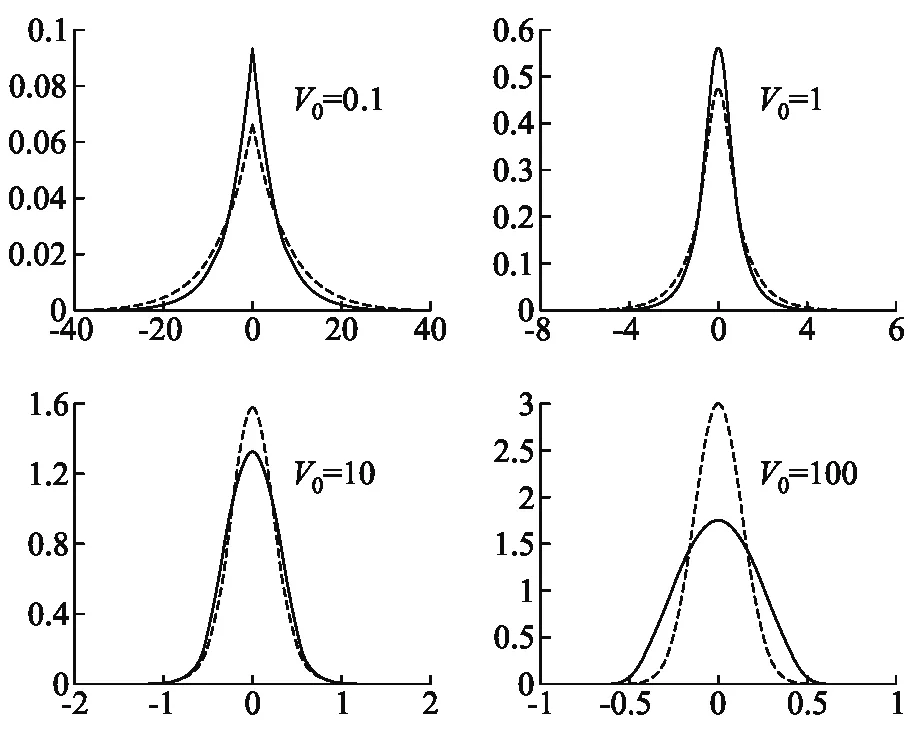
图4 基态粒子的位置概率分布(已归一化)
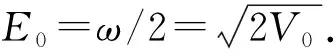
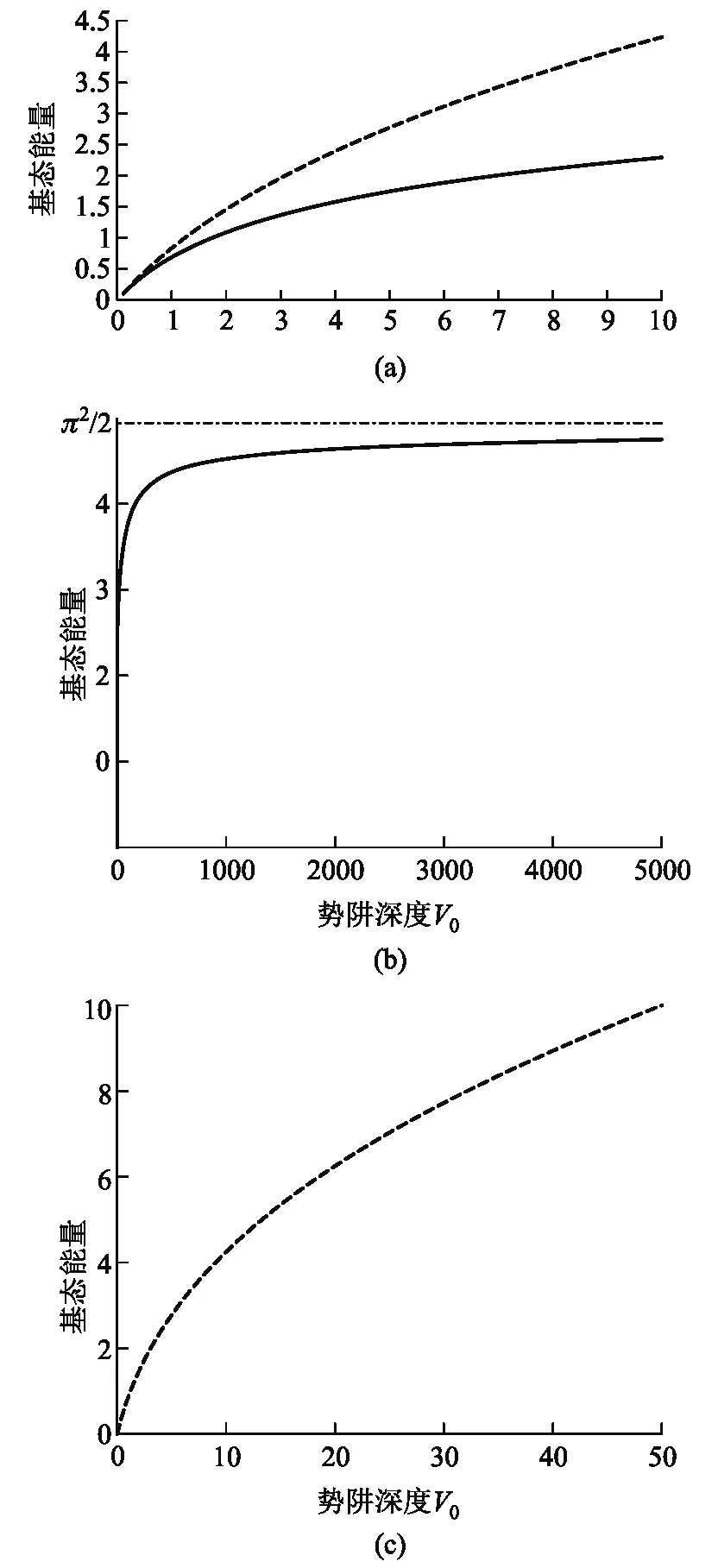
图5 基态能量与势阱深度 V0 的关系图
3 结论
本文介绍了利用多项式插值推导差分公式的方法.本方法既可以推导出精度更高的差分公式(例如用七点插值),也可以推导出任意阶导数的差分公式.当然,差分公式的精度越高,计算量也会越大,我们需要结合实际情况选择最合适的差分公式.
在差分法求解一维定态薛定谔方程时,我们建议选择四阶精度的差分公式,因为其计算量并不比二阶精度的差分公式大太多,但能把计算精度提高两个阶次.
