格林函数以及在常微分方程中的应用
2021-09-16钱光耀闫若琨汪泽西郑神州
钱光耀,闫若琨,汪泽西,郑神州
(北京交通大学 理学院,北京 100044)
数学物理方程问题通常是表示一种特定的“场”和产生这种场的“源”之间的关系,当源被分解成很多点源叠加时,若设法知道点源产生的场,利用叠加原理,就可以求出同样边界条件下任意源的场,这种求解数学物理方程的方法就是所谓的格林函数法.故格林函数在求解常微分方程边值问题和偏微分方程边值问题、初边值问题有着特殊的重要性,其在特定区域上的电磁场理论、凝聚态物理学、地震工程学、工程材料力学和各种实际物理问题都有重要的应用[1-3]. 以众所周知的静电场为例:在一个区域Ω中某点上放置一个单位正电荷在保持区域边界为零电势情况下,在区域内部产生的电势就是格林函数[4],换句话:格林函数是Δu=δ(ξ),ξ∈Ω满足u|Ω=0的解u=G(x|ξ),x∈Ω;拉普拉斯算子的格林函数的实际表达式在一般区域上是很难得到的,但对于特殊的规则区域,是可以具体用初等表达式表示;一旦有了格林函数,基于线性问题的叠加,就可以得出原定解问题的解的表示[4,5](连续问题用积分卷积表示,离散问题用级数卷积表示).线性微分方程最重要的性质就是叠加原理,故一个复杂的系统可以分解为简单系统叠加.格林函数法的理论意义在于将具有非齐次项和任意边界的定解问题归结为一个特定的边值问题,其表达式仅依赖于微分算子、区域形状和边界形式[5,6].考虑到常微分方程解函数是定义在一维区间上,不需要考虑区域的复杂性,以及文献中各种常微分方程问题格林函数计算和应用的系统性不全[4-7].本文仅以常用的一阶、二阶和高阶常微分方程初、边值为例,综述常微分方程的格林函数的计算法,以及考虑其在线性常微分方程边值问题和初值问题求形式解中的应用.
1 一阶常微分方程初值问题和格林函数
1.1 解的格林函数表示
考虑一阶线性常微分方程
L(y)=y′+p(x)y=f(x),x>a
(1)
在初始条件:y(a)=0下的解.其格林函数G(x|ξ)为下述满足单位点源方程初始条件的解L(G(x|ξ))=δ(x-ξ),G(a|ξ)=0.下面用格林函数来表示方程(1)的y(x).首先对方程L(G(x|ξ))=δ(x-ξ)左右两边同乘f(ξ),得
G′(x|ξ)f(ξ)+p(x)G(x|ξ)f(ξ)=δ(x-ξ)f(ξ)
再对等号两边积分


即

与L(y)=y′+p(x)y=f(x)的对应项比较,得到

(2)
1.2 格林函数表达式
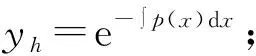
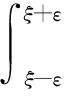
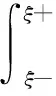
由p(x)G(x|ξ)<∞, 让ε趋于0,可得
G(ξ+|ξ)-G(ξ-|ξ)=1
(3)
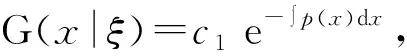
利用式(3),我们可得c=1, 所以
引入Heaviside方程,解表为
(4)

2 二阶常微分方程边值问题和格林函数
2.1 初值问题解的表示
考虑二阶非齐次微分方程:
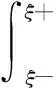
L(y)=y″+p(x)y′+q(x)y=f(x),a (5) 同时满足边界条件: 利用格林函数定义,则有 G″(x|ξ)+p(x)G′(x|ξ)+q(x)G(x|ξ)=δ(x-ξ) (6) 由于x≠ξ满足的齐次线性方程的叠加原理,设其解形式为 可以断定G(x|ξ)在x=ξ连续的:若G(x|ξ)在x=ξ跳跃,则G′(x|ξ)与δ(x-ξ)有相同的奇性, 那么G″(x|ξ)具有比δ(x-ξ)更高奇异性,则式(6)无法成立.所以格林函数G(x|ξ)在x=ξ处一定连续,即:G(x|ξ)|x→ξ-=G(x|ξ)|x→ξ+,从而 c1y1(ξ)+c2y2(ξ)=d1y1(ξ)+d2y2(ξ) (7) 对式(6)在ξ的邻域(ξ-ε,ξ+ε)积分,并令ε趋于0,得 (8) d1y′1(ξ)+d2y′2(ξ)-c1y′1(ξ)-c2y′2(ξ)=1 (9) 最终,根据边界条件和式(7)、(9)可以解出c1、c2、d1、d2. 由于叠加原理,考虑二阶线性常微分方程 L(y)=y″+p(x)y′+q(x)y=f(x),a (10) 在初值条件下:y(a)=γ1,y′(a)=γ2有形式解y=u+v,其中 u″+p(x)u′+q(x)u=f(x),u(a)=0,u′(a)=0, v″+p(x)v′+q(x)v=0,v(a)=γ1,v′(a)=γ2. 考虑Sturm-Liouville方程(散度型方程) L(y)=(p(x)y′)′+q(x)y=f(x) (11) (12) c1(ξ)y1(ξ)-c2(ξ)y2(ξ)=0, (13) 因为算子L和积分可以交换顺序,那么Sturm-Liouville问题的解为 (14) 依据叠加原理,考虑二阶线性常微分方程: L(y)=y″+p(x)y′+q(x)y=f(x),a 在不混合边界条件下α1y(a)+α2y′(a)=γ1,β1y(b)+β2y′(b)=γ2的形式解:y=u+v,其中 u″+p(x)u′+q(x)u=f(x), (15) (16) 考虑二阶线性常微分方程: L(y)=y″+p(x)y′+q(x)y=f(x),a 在如下混合边界条件: B1[y]=α11y(a)+α12y′(a)+β11y(b)+ β12y′(b)=γ1 B2[y]=α21y(a)+α22y′(a)+β21y(b)+ β22y′(b)=γ2 的形式解y=u+v, 其中 u″+p(x)u′+q(x)u=f(x),B1[u]=0,B2[u]=0 v″+p(x)v′+q(x)v=0,B1[v]=γ1,B2[v]=γ2 这里也只考虑齐次问题v有唯一解情况;令y1,y2是齐次方程不为零的基本解且满足边界条件B1[y1]=0,B2[y2]=0.齐次方程在齐次边界下只有零解,故可得B1[y2]与B2[y1]不为零.v的解有下列形式v=c1y1+c2y2.对于u的格林函数满足 G″(x|ξ)+p(x)G′(x|ξ)+q(x)G(x|ξ)=δ(x-ξ) B1[G]=0,B2[G]=0 考虑Green函数的连续性和跳跃性条件 G(ξ-|ξ)=G(ξ+|ξ),G′(ξ+|ξ)-G′(ξ-|ξ)=-1 由于G(x|ξ)=H(x-ξ)uξ(x)是上述待解方程在G(0)=0,G′(0)=1的解,故格林函数有形式解:G(x|ξ)=H(x-ξ)yξ(x)+c1y1(x)+c2y2(x).这个形式解的连续性和跳跃性条件自动满足, 应用边界条件: B1[G]=B1[H(x-ξ)yξ]+c2B1[y2]=0, B2[G]=B2[H(x-ξ)yξ]+c1B2[y1]=0 求解出c1,c2代入上式可得 G(x|ξ)=H(x-ξ)yξ(x)- (17) (18) 考虑一般的n阶线性微分方程: L(y)=y(n)+pn-1(x)y(n-1)+…+p1(x)y′+ p0y=f(x),a (19) 下面用格林函数来构造这个解y.令{y1,y2…,yn}是一组线性无关的解集,那么v就有如下形式v=c1y1+…+cnyn,其中常数是由如下方程所确定: (20) 为了解出u,考虑格林函数满足的方程L(G(x|ξ))=δ(x-ξ),Bj(G)=0.若G(n-2)(x|ξ)在x=ξ跳跃,则G(n-1)(x|ξ)与δ(x-ξ)有相同的奇异性, G(n)(x|ξ)具有比δ(x-ξ)更高奇异性, 这是无法成立的.故G(n-2)(x|ξ)在x=ξ处连续,同理G(x|ξ),G′(x|ξ),…,G(n-2)(x|ξ)也在x=ξ处连续.则有 用分部积分 G(n-1)(ξ+|ξ)-G(n-1)(ξ-|ξ) 其中 于是 所以yξ(x)是满足下列条件的齐次解的线性组合:yξ(ξ)=0,y′ξ(ξ)=0,…,y(n-2)ξ(ξ)=0,y(n-1)ξ(ξ)=1.在x<ξ时,完全齐次方程的解为零解, 故特解yc≡0.在x>ξ时, 设解yc(x)满足上述的yξ的条件,其中yc=λ1y1+λ2y2+…+λnyn,代入上述n个约束条件,由朗斯基行列式恒不为零,可得yc有唯一解,整合后可得一个特解:yc(x)=H(x-ξ)yξ(x).那么格林函数有形式: G(x|ξ)=H(x-ξ)yξ(x)+d1y1(x)+…+dnyn(x) 其中常数是由如下方程所确定 (21)

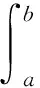
2.2 格林函数的计算
3 二阶微分方程初值问题和格林函数
4 Sturm-Liouville问题和格林函数

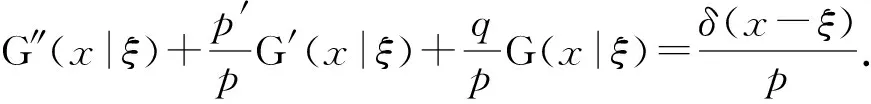
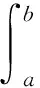
5 不混合边值问题和格林函数
α1u(a)+α2u′(a)=0,
β1u(b)+β2u′(b)=0,
v″+p(x)v′+q(x)v=0,
α1v(a)+α2v′(a)=γ1,
β1v(b)+β2v(b)=γ2

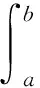
6 混合边值问题和格林函数

7 高阶常微分方程边值问题和格林函数






