拉格朗日陀螺转动的有效势能和可视化
2021-09-16周群益周丽丽莫云飞侯兆阳
周群益,周丽丽,莫云飞,侯兆阳
(1.广州理工学院通识教育学院,广东 广州 510540;2.赣南医学院 医院信息工程学院,江西 赣州 341000;3.长沙学院 电子信息与电气工程学院,湖南 长沙 410022;4.长安大学 理学院应用物理系,陕西 西安 710064)
在重力场中定点转动的对称陀螺又称为拉格朗日陀螺.刘贤雨同学根据柯尼西定理列出了陀螺的动能公式,形成了拉格朗日函数,推导了3个运动积分,进而得出了机械能守恒公式和有效势能公式[1].论文中的机械能守恒公式和有效势能的公式与国内有关教材中的公式都不相同,曲线不能直观地说明有效势能变化规律和陀螺运动的稳定性.本文根据刚体的运动学方程和陀螺运动的动力学方程重新推导了有效势能的公式,绘制了有效势能的曲线族,说明了陀螺运动的类型和稳定性.
1 拉格朗日陀螺的机械能守恒定律
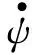
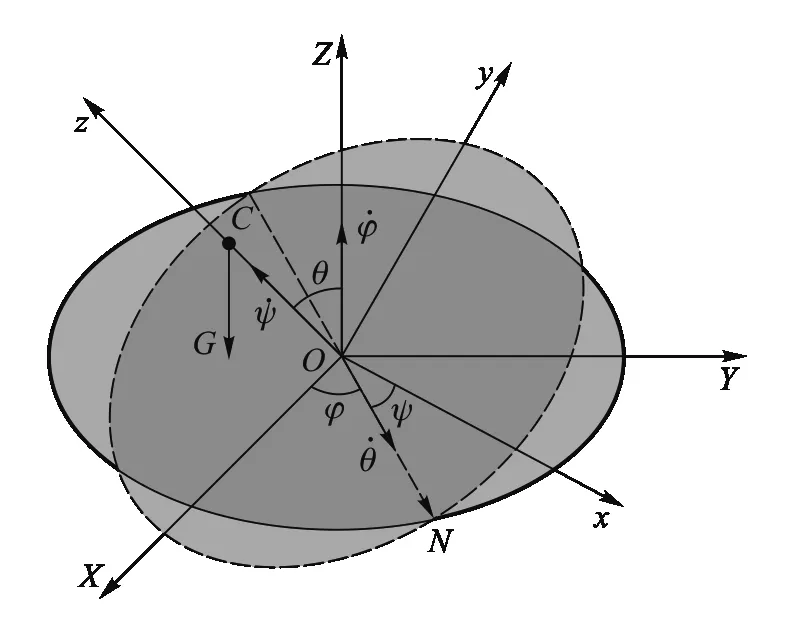
图1 刚体转动的3个欧拉角和角速度的方向
在活动坐标系Oxyz中,陀螺的角速度为
ω=ωxi+ωyj+ωzk
(1)
利用角度关系可得
(2)
这就是欧拉运动学方程.欧拉动力学方程为
(3)
其中,Mx,My和Mz是外力矩的三个分量.
质心C对支点O的位矢为
rC=lk
(4)
其中k是Oz轴的单位矢量.在固定坐标系OXYZ中,OZ方向的单位矢量为K,用动坐标系的单位矢量和欧拉角可表示为
K=sinθsinψi+sinθcosψj+cosθk
(5)
重力可表示为
FG=-mgK=-mg(sinθsinψi+sinθcosψj+cosθk)
(6)
重力对支点的力矩为
M=rC×G=mgl(sinθsinψi-sinθcosψj)
(7)
陀螺的动力学方程为
(8)
对方程组求解,可得出一些重要结果:
1) 对式(8)的第三式积分可得
J3ωz=Lz(常量)
(9)
其中,积分常量Lz是角动量L在Oz方向的投影.这是Oz方向角动量守恒公式.由于陀螺绕Oz轴的转动惯量为J3,角速度为ωz,Lz就是绕Oz轴的角动量.由于J3是常量,所以角速度ωz也是常量.
2) 由式(8)的前两式可得
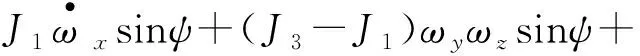
多次利用式(2),经过比较复杂的推导可得
积分可得
J1ωxsinψsinθ+J1ωycosψsinθ+J3ωzcosθ=L0
(10)
其中,积分常量L0是角动量L在OZ方向的投影.这是OZ方向角动量守恒公式.
3) 由式(8)的前两式可得
将式(2)的前两式代入上式可得
即
J1ωxdωx+J1ωydωy-mglsinθdθ=0
积分可得
(11)
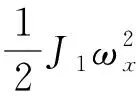
(12)
其中,E也是能量常数:
(13)
如果将E当作陀螺的全部能量,那么E0就是部分能量,在下面的讨论中只需要利用部分能量就行了.
有些教材根据角动量守恒定律推导了公式(9)和(10)[2-4],有些教材利用拉格朗日函数推导了公式(9)和(10)[5-6].这些教材都根据机械能守恒定律得到了式(12).
将式(2)的前两式代入式(12),可得
(14)
将式(2)的前两式代入式(10),可得
(15)
将上式代入式(14),可得能量守恒公式:
(16)
文献[1]用拉格朗日函数求出两个角动量守恒公式,再列出机械能守恒公式(14),用本文的符号表示如下:
2 拉格朗日陀螺的有效势能
由于文献[1]中的式(14)的错误,得出的有效势能公式也是错误的:
由式(16)可得正确的有效势能公式
(17)
对有效势能求导数,可得
(18)
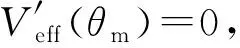
有效势能的二阶导数为
mglcosθ
(19)
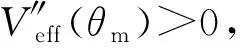
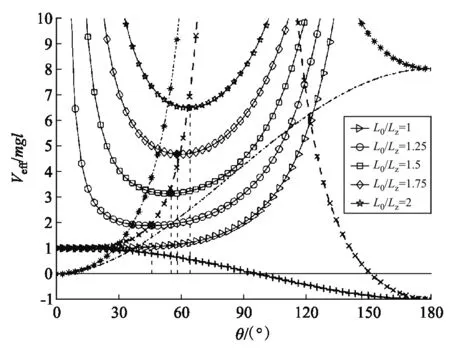
在有效势能的公式中,m、l和J1是常数,L0和Lz是可调节的参数,参数决定了陀螺的运动状态.
2.1 当Lz=0时的有效势能
当Lz= 0时,必有ωz= 0,由式(17)可化简有效势能
(20)
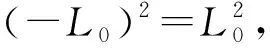
(21)
由式(19)可化简其二阶导数:
(22)
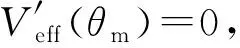
(23)
显然π/2 <θm≤π.将上式代入式(22)可得
(24)
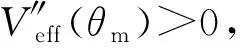
(25)
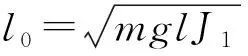
(26)
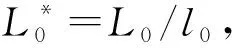
(27)
由式(24)可得平衡角无量纲的二阶导数
(28)
将公式无量纲化便于应用MATLAB画曲线和曲线族,从曲线中解读隐含的信息[7].
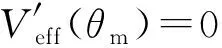
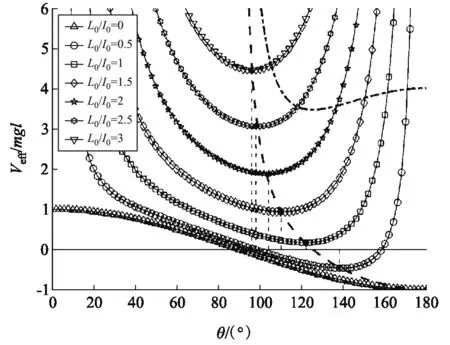
图2 陀螺在Lz = 0时的有效势能
2.2 当Lz = -L0时的有效势能
当Lz= -L0≠ 0时,由式(17)可化简有效势能
(29)
由式(18)可化简其导数,
(30)
由式(19)可化简其二阶导数,
(31)
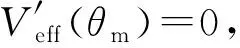
(32)
说明θm=π是稳定的平衡角.
很容易将有效势能和它的导数以及二阶导数无量纲化.
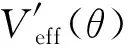
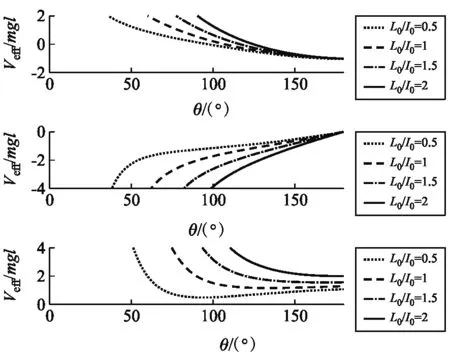
图3 陀螺在Lz = -L0时的有效势能和导数以及二阶导数
2.3 当Lz = L0时的有效势能
当Lz=L0≠0时,由式(17)可化简有效势能
(33)
由式(18)可化简其导数
(34)
由式(19)可化简其二阶导数
(35)
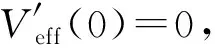
(36)
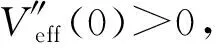
(37)
对上式再求导数,
(38)
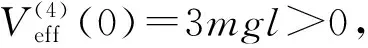
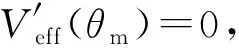
(39)
在L0< 2l0的情况下,还有一个平衡角:
(40)
将式(39)代入式(35),可得
(41)
说明θm是有效势能的极小点,因此θm是稳定的平衡角.可见:当Lz=L0时,如果L0< 2l0,即:陀螺转得不够快,就不能倒立在支点上旋转,而只能以不为零的章动角θm旋转.将式(39)代入式(33),可得平衡角的有效势能:
(42)
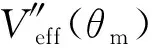
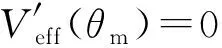
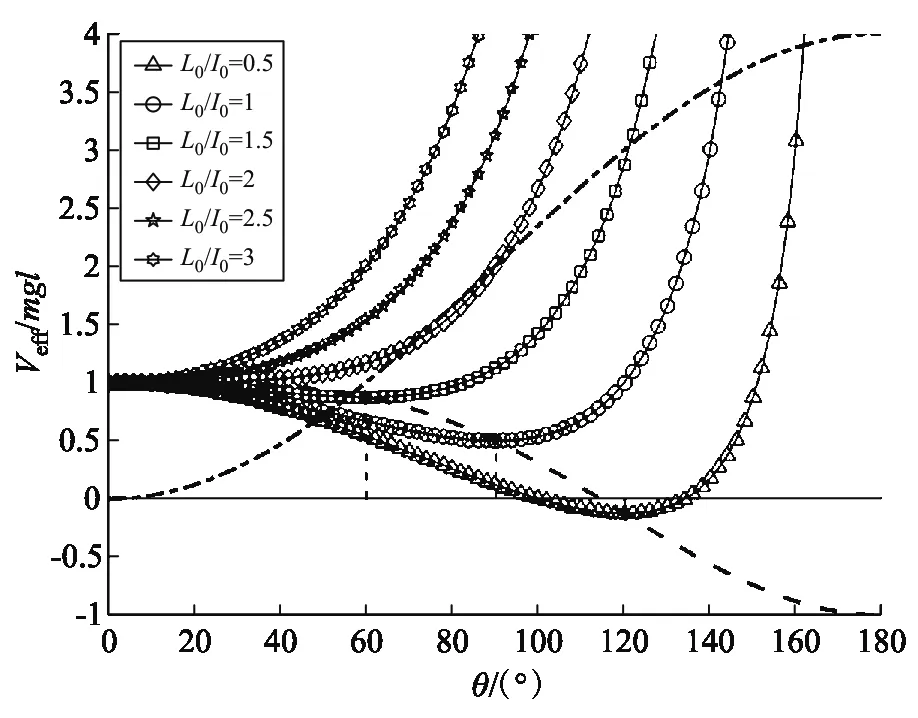
图4 陀螺在Lz = L0时的有效势能
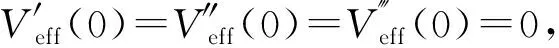
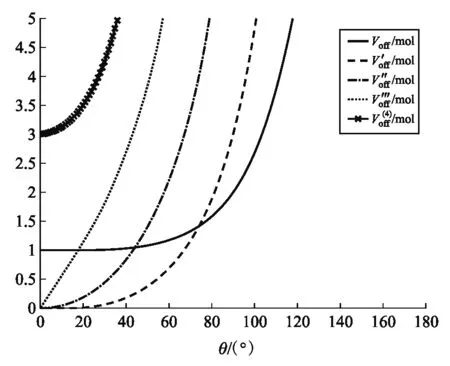
图5 陀螺在Lz = L0 = 2l0时的有效势能和各阶导数
2.4 一般情况下的有效势能
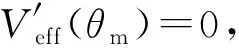
(43)
其中
(44)
当θm=π时,则a= -1,b= -2Lz,c= -Lz2,由式(43)解得L0= -Lz.当θm= 0时,则a= 1,b= -2Lz,c=Lz2,由式(43)解得L0=Lz.当0 <θm<π时,根的判别式为
(45)
其中,D是更简单的根的判别式:
(46)
假设D≥ 0,由式(43)解得
(47)
这是角动量L0与Lz和θm之间的关系.当Lz一定时,如果D> 0,在0 <θm<π范围内,除了θm=π/2之外,同一个θm对应着两个值L0.将上式代入式(17),可得θm处的有效势能:
(48)
当θm→π-时,Veff(θm)→-mgl=Veff(π);当θm→0+时,Veff(θm)→mgl=Veff(0).如果式(48)取正号,当θm→π/2时,Veff(θm)→+∞,θm= π/2是无穷间断点.如果式(48)取负号,可以证明:
(49)
因此,θm=π/2是可去间断点.
将式(47)代入式(19),可得平衡角θm的二阶导数:
(50)
注意:当θm→π-时,由式(47)可得L0→-Lz,由上式可得
(51)
(52)
因此,θm= 0处的稳定性应该由式(36)判断,也可以由上式判断.
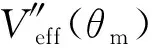
(53)
因此,θm= π/2是可去间断点.由于这个极限大于零,所以θm= π/2是稳定的平衡角.
无量纲的有效势能为
(54)
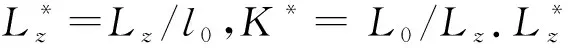
(55)
无量纲的二阶导数为
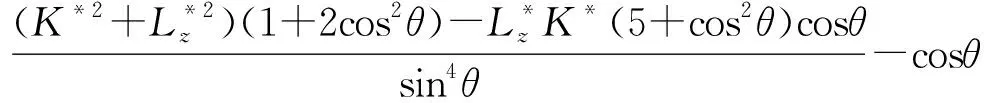
(56)
平衡角无量纲的有效势能为
(57)
其中,无量纲的根的判别式为
(58)
平衡角无量纲的二阶导数为
(59)
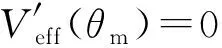
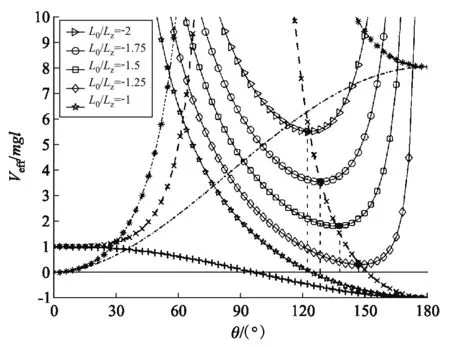
图6 陀螺在Lz = 2l0时的有效势能(L0 ≤ -Lz)
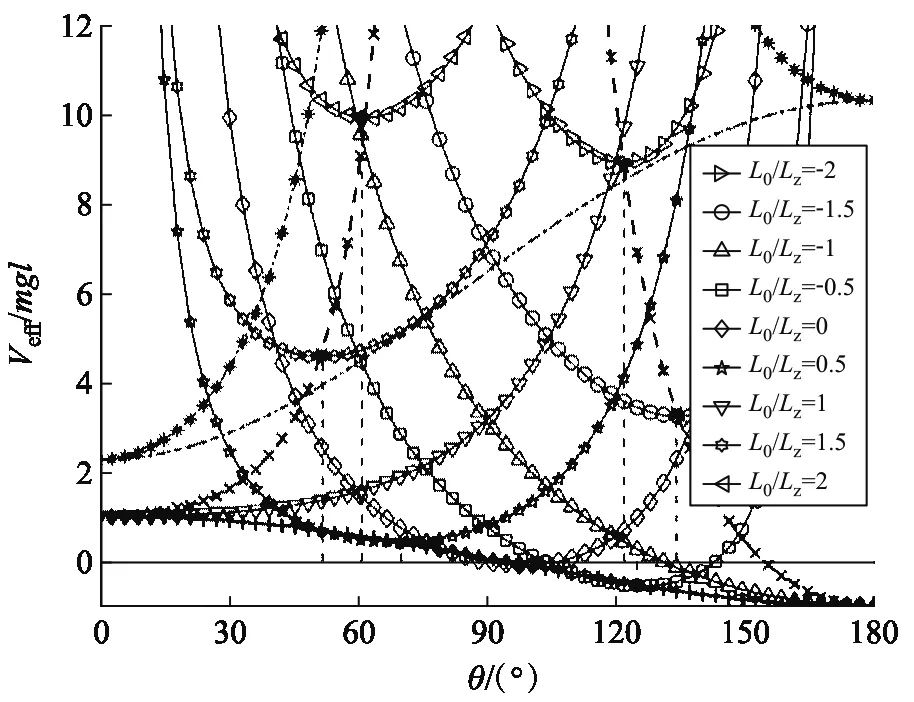
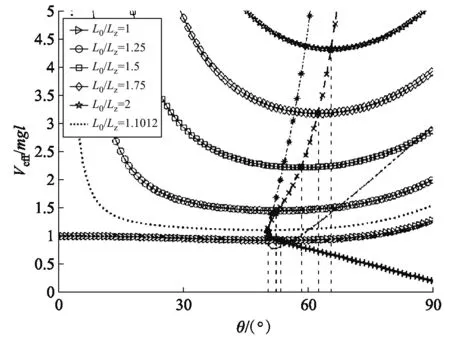
如图7所示,当-Lz 图7 陀螺在Lz = 2l0时的有效势能(-Lz ≤ L0 ≤ Lz) 如图8所示,当L0>Lz时,Veff(θ)还是先降后升的曲线族,但是极小值分布在上支左段上;L0越大,Veff(θm)就越大.当L0=Lz时,Veff(θ)是单调上升的曲线,极小值位于Veff(θm)的上支左段和下支的交点上(0,mgl).可见:θm的稳定分布区域为[0,π/2],陀螺质心只能在上半球面做规则进动. 图8 陀螺在Lz = 2l0时的有效势能(L0 ≥ Lz) 图9 陀螺在Lz = 2.4l0时的有效势能 当E0=Veff(θm)时,陀螺做规则进动,对同一个θm,上支的E0较大,表示快规则进动,下支的E0较小,表示慢规则进动. 3) 当Lz< 2l0时,令D= 0,可得临界稳定角θmC与角动量Lz的关系: (60) 显然,0 ≤θmC≤π/2.θmC是下支与上支左段相交时稳定的章动角.利用上式,式(47)可化为 (61) 这是临界条件下两个角动量之间的关系.当D= 0时,由式(48)可得临界有效势能 (62) 由式(50)可得临界有效势能的二阶导数 (63) 将公式无量纲化即可绘制曲线. 图10 陀螺在Lz = 1.6l0时的有效势能(L0 ≥ Lz) 当0 利用有效势能,可以求章动角的周期,还可以求章动角受微扰的周期.如果设u= cosθ,就可以将式(16)化为u的微分方程,引入椭圆积分就能求出θ(t)的表达式,进而求出两个周期的表达式.本文受篇幅所限,无法详述. 本文求出推导了陀螺运动的有效势能公式和导数公式,将公式无量纲化,应用MATLAB画出曲线和曲线族,详细地说明了陀螺运动的稳定性.刘贤雨同学作为00后的本科生,分析了陀螺在重力场中转动的类型,展现了本科生科研能力和创新能力.MATLAB是一种计算和绘图功能都十分强大的工具,可以推导和验证公式,还能展现问题的每个细节.MATLAB不但能够研究陀螺的有效势能,还能精确地计算章动角的变化范围和周期以及运动规律,精密绘制陀螺质心的轨迹.如果本科生掌握了这种工具,将如虎添翼,大大提高大学生提出问题和解决问题的能力.
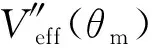
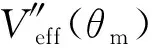
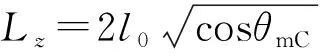
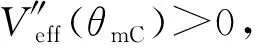
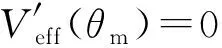
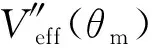
3 结论
