电磁式电压互感器“低频过电压激励-响应”逆问题求解

杨 鸣 熊 钊 司马文霞 李永福 何东升 邹滨阳

（1. 输配电装备及系统安全与新技术国家重点实验室（重庆大学） 重庆 400030 2. 国网重庆市电力公司重庆电力科学研究院 重庆 401123 3. 国家智能电网输配电设备质量监督检验中心 东莞 523325）

0 引言

电力系统中的电压传感装置大多是将高电压转换为可直接测量的低电压信号，实现对电力系统电压状态的实时观测，其传感过程的数学本质是电力系统电压“激励-响应”正问题，即已知传感装置的端口电压传变特性和一次激励电压，获得与一次激励电压具有映射关系的二次响应[1]。通过传感装置测量电力系统高电压的本质是电压“激励-响应”逆问题的求解，也即已知传感装置二次响应及其传变特性，求解获得其一次激励电压。

电磁式电压互感器（Potential Transformer, PT）是35kV及以下交流电力系统中大规模应用的电压传感装置。额定工况下，PT电压“激励-响应”逆问题的求解可简化为：将二次响应电压按变比进行齐次性放大而获得具有极高精度的一次激励电压。然而，由于PT具有频率特性和铁心非线性特性，在高幅值工频过电压、铁磁谐振、直流偏磁等电磁暂态电压作用下，PT铁心可能会出现饱和，其中最为典型的是铁磁谐振，当PT与整个系统的对地电容构成特殊的单相或三相共振回路，满足发生铁磁谐振的参数条件时就会出现铁磁谐振，造成系统中产生较严重的谐振过电压、过电流导致设备损坏[2]，若按变比对电压“激励-响应”逆问题进行求解，会导致测量电压的波形畸变、误差激增，对电能质量监测、暂态电压感知、事故溯源等产生严重影响[3]。因此，亟需实时监测电力系统运行状态，包括各种复杂工况和故障情况下的电磁暂态特性，得到精确的暂态电压波形，以支撑电网的安全运行。

通过PT获得电力系统宽频或宽幅电压的关键是准确求解PT电压“激励-响应”逆问题，需提出表征PT电压传变特性的逆向数学模型及其求解方法，其中PT逆向数学模型是PT正向模型的逆函数[4]。因此，求解“激励-响应”逆问题的基础是构建能够准确表征宽频、宽幅电压激励下PT电压传变特性的正向模型[5]。目前，国内外学者提出的PT正向模型及其“激励-响应”逆问题求解方法主要分为两类。

一类是根据黑盒模型理论和扫频测量技术建立PT正向宽频模型[6]，基于矢量匹配法结合时域递归卷积逆向求解暂态电压，能够通过PT二次侧高度畸变的雷电电压响应计算得到具有较高精度的一次雷电电压。然而，PT铁心具有非线性励磁特性，铁心极易饱和而引起二次波形失真[7]。该正向高频模型参数辨识所采用的测量设备与技术难以精确地将PT铁心非线性特性纳入模型考量[8]，来准确表征铁心饱和时的正向电磁暂态传变特性。因此，当低频过电压激励导致PT铁心饱和时，该模型和方法不适用于一次激励电压的逆向求解。

另一类是建立PT正向电路模型，根据其拓扑结构和元件详细参数进行暂态电压的逆向计算[9]。雷电电压激励下，PT端口电压传输特性主要考虑导体间杂散电容的影响[10]，在传统电路模型的基础上增加合适的电容，可表征高频电压激励下的PT传输特性，实现基于电路模型进行雷电电压激励的逆向求解[11]。在低频暂态电压的激励下，PT传输特性主要取决于短路阻抗和饱和特性等[12]。其中，通过建立电路模型表征PT铁心饱和特性时存在难题：铁心深度饱和状态下，励磁曲线膝点之后数据难以获取[13]。因此，现有PT正向电路模型难以支撑铁心饱和状态下的一次侧暂态电压逆向求解。

综上，低频暂态电压激励下PT二次响应测量误差激增的主要原因是铁心饱和导致其传输特性发生变化。PT作为一种仪用变压器，其结构、电磁暂态模型与电力变压器类似，依据拓扑，其电磁暂态模型可分为T、Γ和π型等效电路模型等[14]。其中，T模型和Γ模型为端口等价模型，均采用单一励磁支路表征铁心的非线性特性，该模型不存在严格的电磁对偶关系。EMTP理论指导书指出：在励磁特性曲线的深度饱和段，变压器类设备芯柱与旁柱的励磁曲线存在明显差异[15]，因此，当PT铁心饱和造成显著的二次电压失真时，T模型和Γ模型不能准确表征其铁心结构上励磁特性的差异，难以准确描述PT饱和状态的电压传输特性[16]。同时，T模型和Γ模型内部参数的物理意义不够明确，当铁心过激励时，模型内部节点电压和支路电流与真实物理状态不具备一一映射关系[17]。因此，将T模型和Γ模型应用于PT一次激励电压逆向求解时会引起较大的计算误差。

π模型采用电磁对偶原理通过严密推导得到，其模型参数物理意义明确[18]。π模型由两条励磁支路构成，可准确表征变压器类设备铁心结构励磁特性的差异，在研究电磁暂态（尤其是深度饱和特性）时具有更高的精度。此外，π模型内部节点电压和支路电流对应于真实物理参数，具有准确求解PT内部真实运行状态的能力。因此，π模型具备求解PT“低频过电压激励-响应”逆问题的潜力。

本文以典型PT为研究对象，以电磁对偶π模型为基础，建立了准确表征铁心非线性特性的PT正向电路模型并进行参数提取[19]，基于正向电路模型构建其逆向数学模型，进而提出含高度非线性元件的离散状态量数值计算方法，求解PT一次暂态电压，实现了PT“低频过电压激励-响应”逆问题的准确求解。最后开展PT低频暂态电压试验，通过电磁暂态仿真与试验，验证本文方法的可行性和有效性。

1 “低频过电压激励-响应”逆问题求解方法

图1 为PT的“低频过电压激励-响应”正问题与逆问题求解示意图。PT“低频过电压激励-响应”逆问题求解的基本思路为：以PT正向电路模型为基础，构建其逆向数学模型并提出模型求解方法，在已知二次侧响应电压波形数据的条件下计算得到其一次激励电压波形数据，实现对电磁暂态电压的获取。

图1 PT暂态电压求解示意图Fig.1 Schematic diagram of the calculation of PT transient voltage

1.1 PT正向电路模型构建方法

基于电磁对偶理论构建PT的π模型电路具有清晰物理意义，有利于提高PT“低频过电压激励-响应”逆问题求解精度，因此本文以π模型为基础建立PT正向电路模型。根据IEEE[8]与CIGRE[11]关于变压器低频暂态模型的规定，低频暂态模型主要考虑其短路阻抗与饱和特性，本文采用常数电阻表征PT的涡流损耗与铁心损耗。考虑铁心饱和特性的PT正向电路模型如图2所示。图2中PT正向电路模型的电磁对偶关系可参见文献[20]，其中Rs1、Rs2分别为一次、二次绕组电阻；Lm1、Lm2、Rm1、Rm2分别为两条励磁支路的励磁电感（非线性）和损耗电阻；iLm1、iLm2和iRm1、iRm2分别为两条励磁支路电流的感性分量和阻性分量；Ls为一次、二次绕组之间的漏感；端口电压与端口电流分别为u1、u2、i1、i2；u3、u4、u5为π模型内部节点电压；N1、N2分别为PT一次、二次绕组匝数。两个理想变压器用于中间电路的归算并为外电路提供接口，可规定为

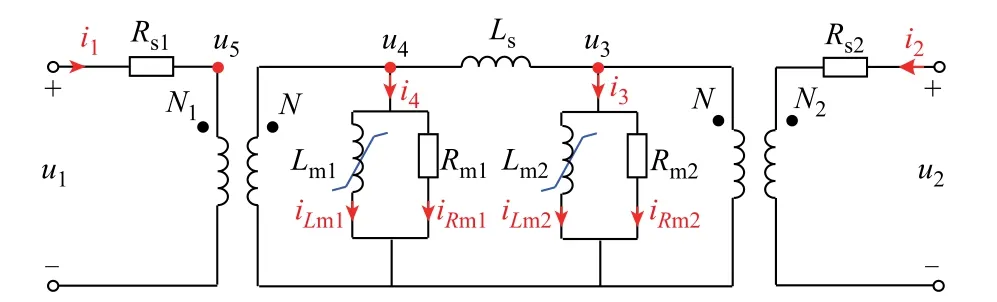
图2 考虑铁心饱和特性的PT正向电路模型Fig.2 Forward circuit model of PT considering the saturation characteristics of the iron core

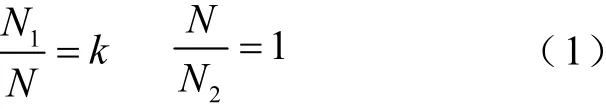
式中，k为PT的额定变比。

1.2 PT正向电路模型参数测量与提取方法

针对本文提出的PT正向电路模型进行参数的测量与提取，通过变压器标准短路试验及开路试验可以获得电路模型短路阻抗、铁损电阻及铁心非深度饱和段励磁曲线。在高幅值低频暂态电压作用下，变压器铁心进入饱和或深度饱和状态，因此，本文通过PT深度饱和试验提取铁心深度饱和状态下模型参数。

1.2.1 非深度饱和段参数提取

1）开路试验

进行PT开路试验，在低压侧施加交流电源，保持高压侧开路，逐渐增加空载电压至铁心轻微饱和，在不同电压幅值下进行多次试验，绘制PT铁心非深度饱和段励磁支路的单值无磁滞励磁曲线。磁链通过端电压的积分进行求解，即

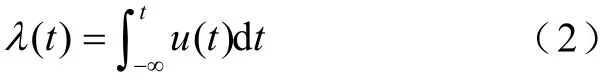
实际应用中，采集到的电压为离散数据，采用梯形积分法计算励磁支路磁链。梯形积分法是一种简单的一步积分法，具有二阶精度，并且在任何时间步长下都不会发散，如式（3）所示。

式中，λ为铁心磁链；u为励磁支路端电压；Δt为采样步长；n=1, 2, 3, …。

铁损和电阻可按式（4）和式（5）计算得到。

式中，P为有功功率；T为电源周期；Urms为电压有效值；Rm为铁损电阻。

连接磁滞回线顶点可得到非深度饱和段基本磁化λ-i曲线。当PT工作在非深度饱和状态时，π模型励磁电感远大于漏感，两励磁支路的励磁特性差异可忽略，可将端口测得的励磁电流平分至两励磁支路，并使两条励磁支路的损耗电阻等于铁损电阻Rm的2倍，保证整体损耗平衡，求解方法为

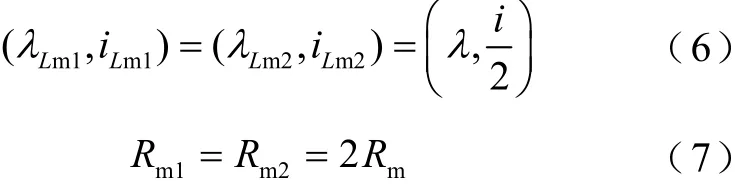
式中，i为PT端口电流；λ为式（3）得到的磁链。

2）短路试验

采用交流电压源对PT进行标准短路试验。PT漏磁参数为式中，Zs为漏阻抗；Rs为绕组电阻；f为电源频率，f=50Hz；Irms为电流有效值。

一次、二次绕组电阻Rs1和Rs2可依据绕组直流电阻Rdc1和Rdc2按比例分配得到，即

1.2.2 深度饱和段参数提取

为获得PT深度饱和特性，本文采用交直流混合电源对PT进行饱和测试，试验电路如图3所示。其中，混合电源中直流分量激励PT铁心进入饱和状态，利用耦合交流小信号测量PT在不同饱和状态下的励磁支路增量电感。深度饱和状态下PT励磁支路电感采用式（12）~式（14）进行计算，仅需一次测试即可计算得到双端口励磁支路参数。

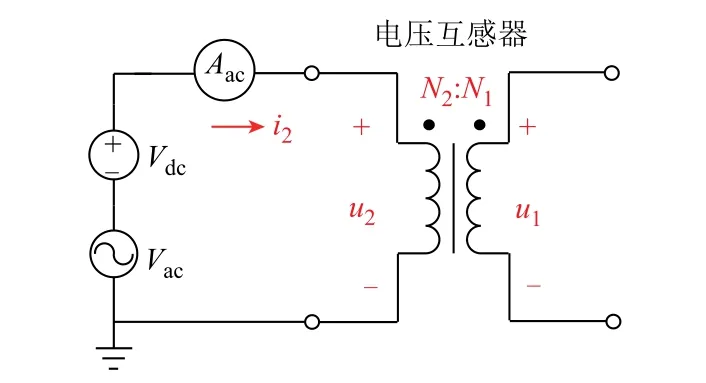
图3 饱和试验原理图Fig.3 Schematic diagram of saturation test

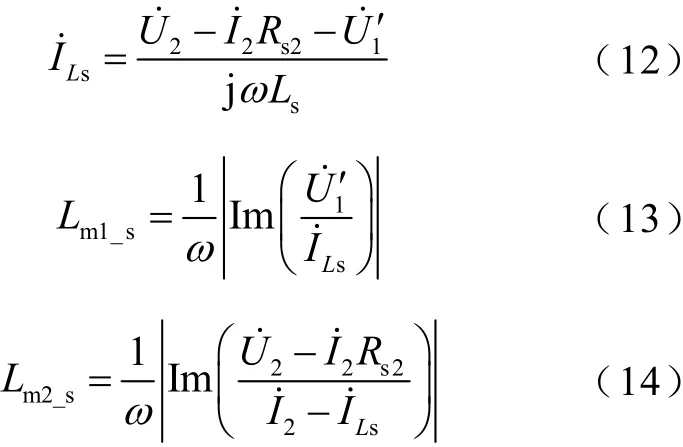
式中，Lm1_s、Lm2_s分别为PT铁心饱和时，一次侧与二次侧励磁支路的增量电感；U˙1′为互感器一次电压折算至二次侧的电压值；U˙2为互感器二次侧端口电压；I2˙为二次侧端口电流相量；I˙Ls为漏感电流；Im(·)用于提取向量的虚部分量。

由交直流混合测试原理可得，励磁曲线斜率可用增量电感值表示。因此，根据文献[20]在铁心不同饱和程度下进行饱和试验，可获得励磁曲线多个饱和点参数，基于多个饱和点计算得到饱和段励磁曲线。随着铁心饱和程度的加深，励磁支路增量电感值（即励磁曲线斜率）逐渐减小。将端口励磁曲线分配至一次侧与二次侧励磁支路的方法如式（15）~式（17）所示。

式中，idc为端口电流直流分量；(λLm1(0),Lm1(0)),(λLm2(0),Lm2(0))为式（6）计算得到的最后一个点，即非深度饱和段基本磁化曲线的顶点。

通过上述参数提取方法，可分段线性表征PT励磁支路电感Lm1和Lm2的深度饱和段励磁特性，结合非深度饱和段励磁参数即可建立完整的考虑铁心饱和特性的PT正向电路模型。PT出厂报告中包含短路试验测试数据，部分PT还将进行励磁特性的测量，并向用户提供励磁曲线[21]。因此，PT厂家仅需额外开展饱和试验即可满足参数辨识需求。

1.3 PT逆向数学模型构建与求解

基于图2所示的PT正向电路模型构建其逆向数学模型，列写节点电压方程，推导一次端口电压，得到PT的逆向数学模型为

式中，u2为实测二次响应电压；u1为待求解的一次激励电压；u4为内部节点电压。

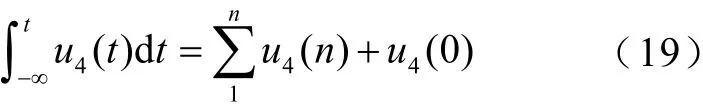
由于实测信号为离散量，因此可将式（18）中电压积分转换为离散点求和，得到

当低频暂态电压作用于PT时，可能造成铁心饱和或深度饱和，此时流过励磁电感的电流iLm1、iLm2与磁链表现为非线性特性，非线性函数表征为

式中，fLm1、fLm2函数表征励磁支路的非线性励磁曲线，包含PT非深度饱和段与深度饱和段的完整励磁特性；磁链λLm1和λLm2均为时间的函数。

励磁支路电感Lm1、Lm2的磁链λLm1、λLm2可采用梯形积分法对励磁支路的电压进行积分得到。

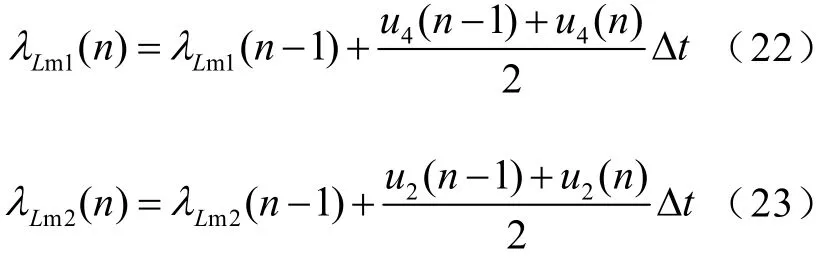
将已知离散电压u2结合式（22）和式（23）代入PT逆向数学模型式（18）中进行逐点计算即可求解得到一次侧激励电压数据，实现PT“低频过电压激励-响应”逆问题的求解。

2 PT正向模型参数测试与提取试验

本文针对JDZ10(G)-10B3型PT进行研究，其铭牌参数见表1。

表1 JDZ10(G)-10B3型PT铭牌参数Tab.1 Nameplate of the JDZ10(G)-10B3 PT

2.1 PT正向模型参数提取

根据第1.2.1节所述的PT非深度饱和段试验与参数提取方法对试验PT进行开路试验和短路试验，模型电阻、电感参数见表2。图4所示为开路试验测得PT的非深度饱和段磁滞回线，连接磁滞回线的顶点得到非深度饱和段励磁曲线。

表2 JDZ10(G)-10B3型PT电阻、电感参数Tab.2 Resistance and inductance parameters of the JDZ10(G)-10B3 PT

图4 JDZ10(G)-10B3型PT磁滞回线Fig.4 Hysteresis loops of the JDZ10(G)-10B3 PT

2.2 励磁电感深度饱和参数测试与提取试验

根据第1.2.2节中PT深度饱和段励磁曲线参数提取方法，对PT进行饱和试验，获得PT饱和段励磁曲线。混合电源由信号发生器（RIGOL DG1000）激励功率放大器（AE TECHRON 7548）实现，可独立调节交流、直流分量，激励PT至不同饱和程度进行测试。

本文对PT铁心不同饱和程度进行多点测试。按式（13）~式（17）计算得到PT励磁支路电流ILm1、ILm2，励磁支路磁链λLm1、λLm2以及励磁支路的增量电感Lm1_s、Lm2_s，JDZ10(G)-10B3型PT饱和点参数见表3。综合PT铁心非深度饱和段励磁点与深度饱和点即可得到PT正向电路模型两条励磁支路的完整励磁曲线。

表3 JDZ10(G)-10B3型PT饱和点参数Tab.3 Saturation points of the JDZ10(G)-10B3 PT

3 PT“低频过电压激励-响应”逆问题求解验证

3.1 基于电磁暂态仿真数据的验证

应用ATP-EMTP电磁暂态软件建立PT暂态电压仿真模型，使用Type-96型非线性电感元件表征铁心非线性特性。在一次侧施加高于额定值的交流电压激励PT铁心进入深度饱和状态，记录低频过电压作用下PT的一次侧、二次侧端口电压波形。仿真电路模型如图5所示，其中，R2为PT二次侧额定负载，分别验证PT负载为0V·A、5V·A、15V·A（额定负载）条件下，暂态电压逆向求解的准确性。

图5 PT ATP仿真模型Fig.5 ATP simulation model of the PT

基于仿真得到的二次电压数据，采用1.3节提出的“低频过电压激励-响应”逆问题求解方法计算一次侧激励电压，额定负载条件下暂态电压逆向求解结果如图6所示。

图6 基于PT仿真数据的逆向求解结果Fig.6 Inverse calculation results based on simulation voltage of the PT

二次归算电压U2′为PT二次端口测量电压值U2与变比k的乘积，其计算方法为

暂态电压求解相对误差可按式（25）和式（26）计算。

方均误差（MSE）可用于反映估计量与被估计量之间的差异程度，本文通过求解方均误差检验归算电压、逆向求解电压对一次真实电压波形的还原程度，即

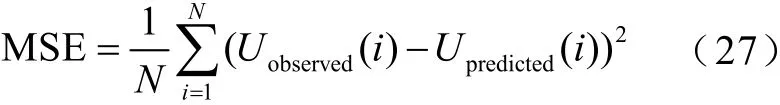
式中，Uobserved为电压观测值，即一次真实电压；Upredicted为电压估计值。

对比分析电磁暂态仿真与一次电压逆向求解结果，在负载分别为0V·A、5V·A、15V·A条件下，归算电压最大误差分别为77.6%、77.7%、78.1%，方均误差最大为0.182，未能准确反映真实激励电压；而本方法逆向求解电压最大误差分别为2.22%、2.24%、2.26%，方均误差最大为0.003 18，可以较好地还原一次真实电压波形，证明本文所提出的逆问题求解方法理论上正确且具有可行性。

3.2 基于真型PT试验数据的验证

3.2.1 真型PT暂态电压激励试验与逆向求解

由于电磁暂态仿真难以模拟实际工况中的不确定性和随机性，基于JDZ10(G)-10B3型PT搭建低频过电压试验平台，如图7所示。其中，AT为试验调压器；T为试验变压器；D为阻容分压器；PT为10kV电磁式电压互感器；C1为交流电源及线缆等效杂散电容；C2为PT端口等效杂散电容；OSD为录波器。

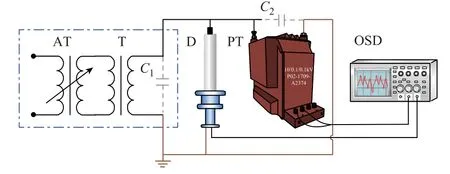
图7 PT暂态电压试验平台Fig.7 Transient voltage test platform of the PT

在PT一次侧施加不同幅值的交流电压激励铁心至饱和，采用标准阻容分压器测得一次侧真实电压波形，并同步记录PT二次侧波形，采用小波阈值去噪法对二次波形进行滤波以降低外部干扰的影响[22]，验证PT发生饱和失真时暂态电压逆向求解的准确性。对比归算电压、实测电压与逆向求解电压，如图8（暂态）与图9（稳态）所示。

图8 基于PT的暂态电压逆向求解结果（暂态部分）Fig.8 Inverse calculation results of transient voltages of PT(transient part)

图9 基于PT的暂态电压逆向求解结果（稳态部分）Fig.9 Inverse calculation results of transient voltages of PT(steady state part)

结果表明，由于电源侧与PT端口均存在杂散电容，造成PT铁心饱和而产生谐振，二次电压发生严重失真。归算电压与一次真实电压在铁心饱和状态下存在较大的误差，无法准确得到真实波形数据，而本文方法可得到较为准确的一次电压波形。

3.2.2 误差分析

按式（24）~式（27）计算基于π模型的低频电压逆向求解误差，结果见表4。

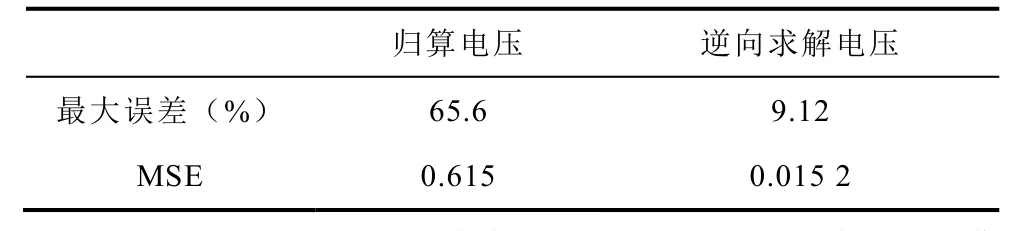
表4 PT低频暂态电压逆向求解误差Tab.4 Errors of the inverse calculation of low frequency transient voltage of PT

由表4可知，通过本文提出的PT正向电路模型与逆向求解方法可将PT的测量误差由65.6%降低至9.12%，MSE由0.615降低至0.015 2，更准确地还原得到一次真实电压波形。

基于本文3.2.1节中PT暂态电压试验，对比分析其一次真实电压、二次归算电压、逆向求解电压的主要谐波分量（如图10所示）。结果表明：逆向求解电压的基波、3次谐波、5次谐波分量误差分别为3.33%、4.42%、7.58%，较为准确地还原了真实激励电压，证明通过本文的方法可以实现基于PT测量低频宽幅值电磁暂态电压。本文研究中主要考虑了PT铁心的饱和特性，忽略了磁滞和涡流效应的影响，因此谐波分量求解仍存在一定误差，后续将改进本文算法以实现PT磁滞特性和绕组涡流特性的准确表征，进一步提高PT暂态电压逆向求解精度。

图10 PT逆向求解电压频谱对比Fig.10 Frequency spectrum comparison of the PT

4 结论

本文提出了一种针对PT“低频过电压激励-响应”逆问题的求解方法，建立了考虑铁心非线性的PT正向电路模型；通过PT端口测试提取其正向模型参数以及铁心深度饱和的励磁数据；基于PT正向电路模型提出其逆向数学模型及模型数值求解方法，通过PT二次侧响应电压计算其一次激励电压；最后以某真型10kV PT为研究对象，通过ATPEMTP软件仿真以及试验验证，证明本文所提出的逆问题求解方法能够还原具有较高精度的一次电压波形，可将PT的低频暂态电压测量误差从65.6%降低至9%，MSE从0.615降低至0.015 8，大幅提高PT量测的频率适用范围。本文方法不需要新增任何一次设备，为电力系统低频电磁暂态电压准确获取提供了有效的解决方案。