基于广义储能的多能源系统不确定优化调度策略

叶 畅 曹 侃 丁 凯 陈 乔 钱一民

（国网湖北省电力有限公司电力科学研究院 武汉 430077）

0 引言

新能源发电的大规模接入逐步改变了我国的能源结构，同时也对传统电力系统的调度运行方式产生了显著影响[1]。风电、光伏发电由于其出力的随机性、波动性和间歇性特性，给电力系统安全稳定运行带来了一定的不利影响。而火电、水电作为装机规模大、调节能力强的可控电源，可有效平抑风电和光伏的出力波动，提高电网消纳可再生能源的能力[2]。

通常，可将风、光、水、火等独立发电系统进行优化配置，形成多种形式的互补发电系统。文献[3]针对风光水互补发电系统与需求侧数据中心的联动，建立了综合考虑经济效益、负荷追踪系数及风光消纳程度的多目标优化调度模型。类似地，文献[4]提出一种考虑需求响应潜力时变性的风电、火电和负荷实时协同控制技术，以实现风电功率的最大消纳。在此基础上，文献[5]引入虚拟电厂的概念，建立了风-光-水-碳捕集多区域虚拟电厂协调优化调度模型，通过区域间综合能源的互联实现多区域电能互补。

为了进一步促进新能源消纳，提升电力系统经济运行水平，有学者提出“能源互联网”概念，采用多能协调互补技术，实现能源的高效利用[6]。能源集线器（Energy Hub, EH）作为能源互联的重要支撑手段，可为能源生产者和消费者之间提供有效接口，实现多种能源的耦合[7-9]。在EH中，除前述电力能源外，还包含冷、热、气等多类型能源[10-11]。EH可满足多种能源之间的转换需求，是能源相互转换、交换和传递的中心。目前，国内外在基于EH的多能源系统能量管理与调度方面已开展了部分研究。文献[12-13]针对能源集线器内部能量流动与交互，提出了智能能量管理策略。文献[14]针对含电/热/气网络的综合能源系统，建立了EH扩展模型，并提出了以综合用能成本较低和用能能效较高为目标的分层优化调度策略。文献[15]引入储热装置，提出了包含能源集线器优化层及网络优化层的综合能源系统分层优化调度策略。考虑到可再生能源发电等不确定性因素，文献[16]针对智慧城市能源系统，建立了考虑机会约束的EH随机优化模型。在此基础上，文献[17]则利用蒙特卡洛方法构建随机场景，提出同时考虑光照、负荷及电价不确定性的多能源系统优化调度策略。

上述研究成果中，通常会配置储能以提高系统调控能力。然而现阶段研究中考虑的大都是传统意义上的常规储能。实际上，适当激励机制作用下的柔性负荷，可在一定程度上实现某个时段内电量或热量需求的增加或减少，其效果类似于传统储能装置，通常可称为虚拟储能，已有文献将传统储能及虚拟储能统称为广义储能（Generalized Energy Storage, GES）[18]。文献[19]研究了可平移负荷、可转移负荷和可削减负荷的响应特性，建立包含实际储能和柔性负荷的广义储能模型，并对广义储能调节能力进行分析。文献[20]则将广义储能应用到综合能源系统中，提出考虑广义储能的区域综合能源系统优化调度策略。

以上研究为含广义储能的多能源系统优化调度提供了有力基础，但仍存在以下局限和不足：①目前多能源系统优化模型中，大都仅将电力柔性负荷作为广义储能的一部分，较少考虑热负荷调节能力对广义储能的贡献；②针对多能源系统中可再生能源出力及需求侧响应不确定性的研究还不够深入，缺乏考虑源荷双侧不确定性的多能源电力系统优化研究；③对储电和储热装置的综合调节特性研究尚有不足，同时较少考虑系统电-热转换特性。

鉴于此，本文考虑源荷双侧不确定性，提出一种基于广义储能的多能源系统不确定优化调度策略。首先，提出考虑热电联供的能源集线器架构，对各电力及热力能源进行建模。针对常规电池储能和储热罐，采用能量状态模型进行统一描述；同时针对虚拟储能，分别采用正态云模型和自回归滑动平均时间序列模型对电、热柔性负荷进行建模，并分析广义储能资源的调节特性。在此基础上，引入可调节鲁棒方法，建立以运行成本最低为目标的多能源系统鲁棒优化调度模型。针对该模型中电源出力及负荷响应的不确定性，采用对偶理论及拉格朗日变换，将含风电及光伏出力不确定性的约束转换为确定性约束；同时利用正态云发生器及场景削减技术得到典型场景，采用Matlab/YALMIP工具箱对模型进行求解。最后，利用算例结果验证了所提策略的可行性及有效性。

1 基于广义储能的多能源系统建模

本文所研究的多能源系统主要包含电网和天然气网。其中电力能源包括外部电网、可再生能源发电（Renewable Energy Generation, REG），热力能源主要指燃气锅炉和电转热装置，此外，还包括具备热电联产功能的燃气轮机。由此，可得到考虑热电联供的能源集线器架构如图1所示。

图1 基于广义储能的能源集线器架构Fig.1 The structure of energy hub based on GES

在图1所示架构中，集电器的电力来源包括电网、可再生能源发电（风电和光伏）、热电联产（Combined Heat and Power, CHP）机组以及储电装置。相对地，集热器的热力来源包括燃气锅炉（Gasfired Boiler, GB）、CHP机组的余热锅炉、电转热装置（Electric to Heat Device, EHD）及储热装置。集电器和集热器分别满足电负荷及热负荷的需求。下面，将分别对上述主要单元进行建模。

1.1 电力及热力能源模型

1.1.1 新能源发电机组

考虑新能源出力不确定性，采用对称不确定区间描述其出力，可表示为

式中， ΔPiREG,t为新能源电站iREG在时段t的实际波动功率，该值为待定量。

1.1.2 CHP机组

CHP机组在运行工况下，可分别产生电功率和热功率。本文中CHP机组采用“以热定电”方式运行，对于小型燃气轮机，其燃料耗量可近似用一次函数表示为[21]

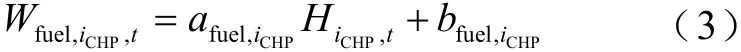
式中，Wfuel,iCHP,t为第iCHP台CHP机组在t时段输入的燃料热量；HiCHP,t为第iCHP台CHP机组在t时段的热功率；afuel,iCHP和bfuel,iCHP分别为第iCHP台CHP机组的燃料耗费系数。

同时，在某一时段内CHP机组的热功率和电功率可用热电比表示为式中，PiCHP,t为第iCHP台CHP机组在t时段的电功率；kiCHP为第iCHP台CHP机组的热电比。

1.1.3 燃气锅炉

燃气锅炉可直接用输入/输出效率模型表示为

式中，H iGB,t为燃气锅炉iGB在时段t产生的热功率；WIN,iGB,t为燃气锅炉iGB在时段t输入的天然气燃料热量；ηiGB为燃气锅炉iGB的气热转换效率。

1.1.4 电转热装置

考虑到风电和光伏的消纳问题，利用可能存在的弃风弃光电量进行电热转换，可进一步提高新能源消纳率，提高多能源系统收益[22]。类似于燃气锅炉，电转热装置也可采用输入/输出效率模型表示为

式中，HiECH,t为电转热装置iECH,t在时段t产生的热功率；PiECH,t为电转热装置iECH,t在时段t输入的电功率；ηiECH为电转热装置的电热转换效率。

1.2 广义储能模型

1.2.1 实际储电/储热装置模型

本文分别采用电池储能（Battery Storage, BS）和储热罐（Thermal Storage, TS）作为实际储电和储热装置，利用能量状态（State of Energy, SOE）建立统一的电/热储能模型，即

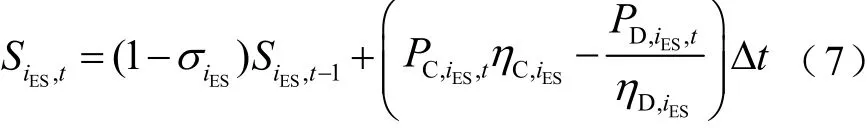
式中，SiES,t和SiES,t−1分别为t时段和t-1时段储能装置iES的SOE；PC,iES,t和PD,iES,t分别为储能装置iES在t时段的蓄电（热）和放电（热）功率；ηC,iES和ηD,iES分别为储能装置iES的蓄电（热）、放电（热）效率；σiES为储能装置iES的自耗率。

1.2.2 虚拟储能模型

前文已指出，通常可将具备调节能力的电力/热柔性负荷作为虚拟储能参与系统调控。

对于电力柔性负荷，考虑可转移负荷和可削减负荷两类。通常，可转移负荷可用价格型需求侧响应模型来描述。由于用户意愿及环境、气候等因素，价格型需求侧响应通常具有不确定性。将电价变化量作为影响用户心理的主要因素，采用正态云分布来描述响应预测误差[23]，可表示为

式中， ΔλRL,Δc为电价差Δc时可转移负荷响应误差；C为正态云分布；Ex、En及He分别为正态云分布的期望、熵和超熵；“~”表示 ΔλRL,Δc服从正态云分布。其中期望Ex与传统概率论中期望的意义相同，表示定量论域U中代表性最强的点；熵En表示论域U中各云滴对于期望值的偏差程度，既可反映云滴的离散程度，也可反映其大致的取值范围；超熵He则是对熵的一种不确定性度量，可看作“熵的熵”，其反映的是误差边界的离散程度。相比传统采用正态分布描述误差变量分布的方式，本文采用的正态云模型既可以用来描述变量的随机分布，也可同时反映随机边界的模糊性，从而更加精确地描述可转移负荷的需求响应误差。

当电价差为cΔ时，负荷响应转移率可表示为

式中，λRL,Δc为电价差Δc时负荷响应预测转移率。

设定系统电价包括峰、平、谷三个阶段，峰-平电价差记为Δ1c，峰-谷电价差记为 2cΔ ，平-谷电价差记为 3cΔ 。为简化计算，假定高电价时段负荷向低电价时段平均转移，因此考虑响应之后的可转移负荷在峰、平、谷时段分别为

式中，PRL,tf、PRL,tp、PRL,tg分别为原峰、平、谷时段的可转移负荷；tf、tp和tg分别为峰、平、谷电价的某一时段，且tf,tp,tg∈t；Tf、Tp和Tg分别为峰、平、谷三个阶段的总时段数。

对于可削减负荷，采用事先与电网签订激励合同，在紧急情况下根据合同进行中断响应的方式参与电网功率调节，可表示为

式中，αiIL,t为第iIL个可削减负荷在t时段内的实际出力状态，1表示正常出力，0表示中断出力；PiIL,t为第iIL个可削减负荷在t时段的实际功率；为第iIL个可削减负荷在t时段的原功率。

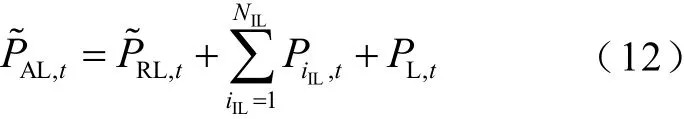
因此，系统在t时段的总电力负荷可表示为式中，P~RL,t为t时段可转移负荷大小；PL,t为t时段刚性电力负荷大小；NIL为可削减负荷的总数量。

对于热负荷而言，用户实际需求为室内温度的高低。由于人体对温度的非实时敏感性，一定范围内的温度变化对于用户来说是可接受的。为体现热负荷的柔性，可采用自回归滑动平均（Autoregressive Moving Average, ARMA）时间序列模型描述，即[24]

式中，Tsupp,t、Tback,t、Tin,t和Tout,t分别为供水温度、回水温度、室内温度和室外温度；αj、βj、γj、θ1、1φ、1ω均为供热系统的热惯性参数；J为ARMA模型的阶数。

由此可得到供热功率为

式中，Hsupp,t为t时段所需的供热功率；c为水的比热容；m为热水的流量。

至此，广义储能模型已建立完毕，各类储能的调节特性对比见表1。

表1 广义储能调节特性对比Tab.1 Characteristics comparison of generalized energy storage

2 多能源系统鲁棒优化调度模型

第1节对电/热力电源以及广义储能进行了建模，本节将针对多能源系统，建立可调节鲁棒优化调度模型。

2.1 目标函数

以系统运行成本最低为目标，可得到目标函数为

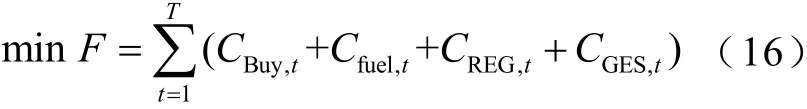
式中，CBuy,t、Cfuel,t、CREG,t和CGES,t分别为外部电网购电成本、天然气购买成本、新能源相关成本及广义储能相关成本。为突出广义储能影响，本文运维成本中仅考虑储能装置的相关成本，则上述各项成本的详细表达式为

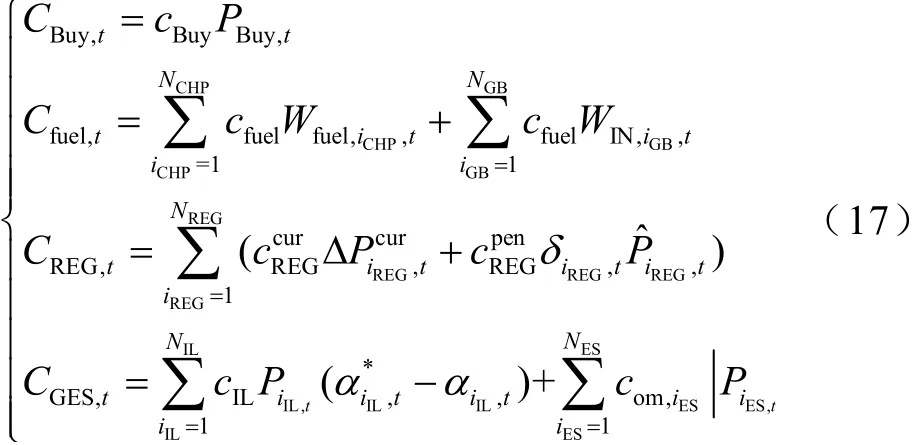
式中，cBuy为外部电网购电电价；PBuy,t为t时段购电功率；cfuel为天然气价格成本；为第iREG种可再生电源的弃电成本系数为第iREG种可再生电源在t时段的弃电功率；为REG出力不确定性惩罚成本系数，其意义表示为了应对可再生能源出力不确定性而增加的备用成本系数；cIL为电力柔性负荷中断成本系数；为可削减负荷的原运行状态；com,iES为第iES个常规储能装置的运维成本系数；PiES,t为常规储能装置在t时段的电（热）功率；NCHP、NGB、NREG和NES分别为CHP机组、燃气锅炉、可再生能源发电机组和常规储能装置的总数量。

2.2 约束条件

对于上述目标函数，除第1节所述部分约束条件外，还需考虑以下约束条件。

1）电力/热力供需平衡约束

在系统运行过程中，需保证每一时刻的电力和热力功率平衡，其表达式为

式中，uC,iBS,t、PC,iBS,t和uD,iBS,t、PD,iBS,t分别为电池储能的充、放电状态和功率；分别为储热装置的蓄、放热状态和功率。

2）CHP机组约束

CHP机组在运行时需满足爬坡约束，即

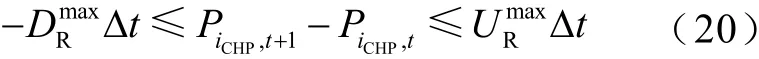
3）实际储能装置约束

储能装置的蓄电（热）、放电（热）约束为

式中，PC,iES,max和PC,iES,min分别为储能装置iES蓄电（热）功率上、下限；PD,iES,max和PD,iES,min分别为储能装置iES放电（热）功率上、下限。

对于储能装置，同一时刻仅存在蓄电（热）或放电（热）中的一种状态，因此有以下储能状态约束

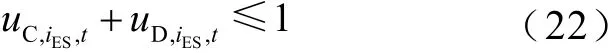
式中，uC,iES,t和uD,iES,t分别为储能装置iES在t时段的蓄电（热）及放电（热）状态，其值为0或1。

储能装置的SOE约束表达式为

式中，SiES,max和SiES,min分别为储能装置iES的SOE上、下限。

4）虚拟储能约束

对于电力虚拟储能，需考虑可削减负荷的中断时间约束以提高用户用电体验，即

式中，Tmin,iIL为在一个调度周期内第iIL个可削减负荷的最小总运行时段；tcon,iIL和分别为第iIL个可削减负荷的连续运行时间和允许最小连续运行时间，以避免可削减负荷频繁投切带来的负荷波动。

对于热力虚拟储能，为保证用户舒适度，室内温度需保持在某一范围内，因此有

式中，Tin,min和Tin,max分别为保持用户舒适度所需的最低和最高温度。

同时，供水温度还应满足

式中，Tsupp,max为系统最大供水温度。

5）系统备用约束

由于系统中主要供电电源为风电和光伏，为了保证多能源系统的稳定供电需求，需要考虑应对新能源出力不确定性的系统备用约束。同时考虑到负荷转移响应的不确定性，系统备用表达式可表示为

式中，PiCHP,max为第iCHP台CHP的最大输出电功率；PBuy,max为多能源系统从电网购电的最大功率；PD,iBS,max为电池储能的最大放电功率；L%为负荷备用系数。

除上述约束外，还应包含各电力电源出力的最大/最小功率约束、各热源的最大/最小放热功率约束及外部电网最大传输功率约束。此外，为了保证储能装置的循环利用效果，各常规储能在调度周期结束时的SOE需与调度周期开始时保持一致。由于篇幅所限，相关表达式将不再赘述。

3 模型求解

以上模型中同时包含基于盒式鲁棒边界的不确定量P~iREG,t及服从正态云分布的不确定量P~AL,t，需对相关约束进行转换处理才能采用常规方法进行求解。文献[25]提供了一种鲁棒对等转换方法，考虑到该方法仅适用于盒式鲁棒优化问题，首先需对P~AL,t进行处理。由于正态云分布的概率密度函数形式复杂，难以得到解析解，因此本文拟引入多场景技术，通过构建典型场景将转换为特定场景中的确定量，进而采用鲁棒对等转换方法处理下面将详细进行阐述。

3.1 基于正向云发生器的多场景构建技术

现有的多场景构建技术常采用随机抽样的方式得到相应的样本，如蒙特卡洛抽样和拉丁超立方抽样等[26]。但对于本文具有正态云分布特征的变量，难以采用上述方法得到符合其分布的样本。因此本文引入正态云发生器工具，将正态云分布由定性概念转换为定量概念，以得到一系列符合数字特征(E x,E n,He)且满足正态云分布的云滴集合。正态云发生的算法步骤为：

（1）设置期望Ex、熵En及超熵He，设置需要产生的云滴个数n。

（2）生成以En为期望、为方差的正态随机数

（3）生成以Ex为期望、为方差的正态随机数

（5）重复步骤（2）~步骤（4），直至产生n个云滴。

将峰-平、峰-谷及平-谷负荷转移率依次记作x1、x2和x3，在采用正向云发生器分别对其进行抽样后，可得到n组样本Xi={xi1,xi2,xi3}，i= 1,2,…,n。一般而言，直接采样后的样本数量较为庞大，可采用文献[27]中的样本削减方法对原样本进行削减，最终可得到数目较少的负荷转移响应典型场景，以及该场景发生的概率1ξ。

3.2 基于可调节鲁棒优化方法的新能源出力不确定性处理方法

在特定概率出现的某一典型场景下，式（18）及式（27）中的负荷均为确定量，此时可对模型进行鲁棒对等转换，以进一步处理新能源出力不确定性问题。

采用线性对偶理论并经适当推导[25]，可将式（27）转换为

式中，λ1,t和λ2,t为的拉格朗日乘子，且满足λ1,t≥ 0,λ2,t≥0。

式（28）中含有新能源电站iREG在时段t的出力波动系数δiREG,t。为了表示系统所有新能源电站总体的出力波动情况，引入鲁棒成本tΓ，tΓ为

通过适当推导，可得到在某一典型场景下系统备用约束被违反的概率2ξ、鲁棒成本tΓ及系统新能源总机组数NREG之间的关系，具体推导过程见文献[28]。

3.3 优化调度模型求解流程

在经过上述两步处理后，原调度模型转换为仅含确定性变量的模型。本文的优化调度模型求解流程可总结为：

（1）利用正态云发生器构建多场景以处理负荷侧不确定性。

（2）采用场景削减技术得到若干典型场景及其概率1ξ。

（3）利用鲁棒对等转换处理电源侧不确定性，得到典型场景下电力备用约束被违反的概率2ξ。

（4）针对发生概率为1ξ的典型场景，通过选取合适的鲁棒成本tΓ值，在电力备用约束被违反的概率为2ξ的情况下，原模型为仅含确定性变量的常规优化模型，可采用Matlab/YALMIP工具箱编程求解。

4 算例仿真

本文所采用的多能源系统中包括两座光伏电站和一座风电站，并与大电网相连。大电网向多能源系统传输的最大功率为1 600kW，考虑到新能源出力波动原因，不允许新能源向大电网倒送功率。算例选取冬季时段，假设两座光伏电站光照条件相同，设定光伏及风力电站实际出力的最大偏差均为日前预测出力的±30%。考虑日前调度，选取调度时段为15min，光伏、风力电站及系统总电力负荷的预测曲线如图2所示。同时，峰-平、峰-谷及平-谷之间的需求侧响应固定转移率分别为0.125、0.312 5及0.062 5。

图2 可再生能源电站及系统总电力负荷预测曲线Fig.2 Prediction curves of renewable energy power stations and electric load

设定CHP的热电比为150%，供热系统的热惯性采用文献[29]中的参数。电网峰、平、谷时段及其对应电价见附表1，CHP机组参数、燃气锅炉参数及电转热参数见附表2，电池储能及储热罐参数见附表3，室外温度变化值见附表4，供热系统初始及最大参数值见附表5。

附表1 电网峰谷平时段及其对应电价App.Tab.1 Time-of-use price of grid

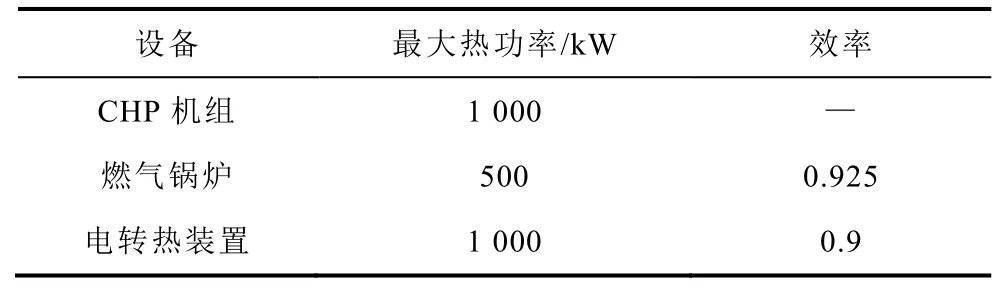
附表2 CHP机组、燃气锅炉、电转热参数App.Tab.2 Parameters of CHP, GB and EHD

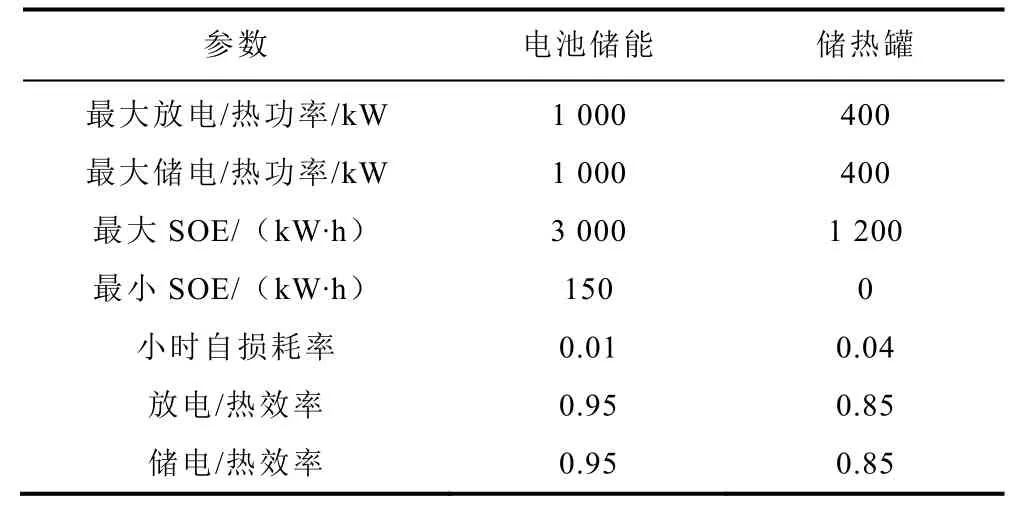
附表3 电池储能、储热罐参数App.Tab.3 Parameters of BS and TS

附表4 室外温度变化值App.Tab.4 Outdoor temperature

附表5 供热系统初始及最大参数值App.Tab.5 Initial and maximum values of heating system（单位：℃）

为了较好地阐述广义储能对系统调节能力的影响，并研究源、荷双侧不确定性对系统运行的影响，考虑以下几种算例情形：

算例1：不考虑广义储能的调节能力，也不考虑源荷双侧的不确定性。

算例2：仅考虑电力柔性负荷的调节能力，不考虑源荷双侧的不确定性。

算例3：同时考虑电力负荷和热负荷的调节能力，不考虑源荷双侧的不确定性。

算例4：同时考虑广义储能的调节能力和源荷双侧的不确定性。

算例程序采用Matlab平台编写，并调用YALMIP工具箱求解。算例1~算例4的仿真结果分别见附图1~附图4，其调度成本依次为31 270元、17 526元、17 118元、22 800元。下面将对仿真结果进行分析。

附图1 算例1仿真结果App.Fig.1 Simulation results of Case 1

4.1 电力柔性负荷对广义储能调节能力的影响分析

电池储能和电力柔性负荷参与电网调控前后，系统等效负荷曲线变化情况如图3所示。

图3 电力柔性负荷需求响应前后的系统负荷曲线Fig.3 Load curves before and after power flexible load demand response

由图3可知，将电力柔性负荷作为广义储能资源参与电网调节后，在负荷高峰时段，柔性负荷吸收负功率；在负荷低谷时段，柔性负荷吸收正功率。由此起到类似于储能“低储高放”的特性，最终实现原峰值负荷转移到负荷谷时段。原电力负荷最大峰谷差为3 488.9kW，算例1等效负荷峰谷差为3 016.3kW，算例2等效负荷峰谷差为2 765.5kW。由此可见，柔性负荷作为广义储能进一步发挥了储能的作用，使得实际等效负荷曲线峰谷差显著降低。

4.2 热柔性负荷对广义储能调节能力的影响分析

固定热负荷下，室内温度恒定设定为24℃；考虑热柔性负荷情况下，室内温度设定为可在22~26℃变化。对比算例2和算例3，考虑热负荷柔性特性前后的热负荷曲线如图4所示。算例3中供热系统的供水温度、回水温度、室内温度变化曲线如图5所示。

图4 考虑热负荷柔性特性前后的热负荷曲线Fig.4 Thermal load curves considering thermal load flexibility

图5 供热系统相应温度变化曲线Fig.5 Temperature change curves of heating system

由图4、图5可知，为了减小供热成本，室内温度通常维持在允许的较小值。但在凌晨2:00~4:00期间，风电出力较大，可能存在新能源弃电时，系统将设定室内温度至较高值，并通过增大电转热装置的实际转换功率，尽可能多地消纳新能源。算例2中新能源弃电电量为353.9 kW⋅h，算例3中新能源弃电量为179.6 kW⋅h，在一定程度上减小了新能源弃电。若增大室内温度的允许范围，如设定室内温度最高可到28℃，则算例3中新能源弃电量减小为33.8 kW⋅h。

4.3 电转热装置对系统运行的影响分析

电转热装置为系统的热-电功率转换提供了桥梁，上述分析中已涉及到相关论述，本小节将从同种情形下电转热装置最大转换功率的角度，对新能源消纳的作用作进一步分析。

如前所述，在夜间新能源出力较大且电负荷较小时，电转热装置会将一部分电能转换为热能进行供热。设定电转热装置的最大热功率为500kW，在一个调度周期内，电转热装置消耗的电量为3 842 kW⋅h，新能源弃电电量为515 kW⋅h。再次设定电转热装置的最大热功率为100kW，此时一个调度周期内电转热装置消耗的电量为1 067 kW⋅h，新能源弃电电量为3 282 kW⋅h。若系统无电转热装置，则此时新能源弃电电量为4 346 kW⋅h。对比以上几种情况可知，电转热装置增加的耗电量与新能源减小的弃电量并不完全相等，因此电转热装置并非简单地消耗多余的新能源电量，而是根据电、热功率平衡，动态地对功率进行调整。

4.4 源荷双侧不确定性对系统运行的影响分析

算例4中，选取系统备用约束被满足的概率不低于75%，则新能源发电对应的鲁棒成本tΓ=2.449 2。同时，通过统计历史运行数据，得到峰-平、峰-谷及平-谷之间的负荷转移率误差分别满足。

以转移率误差 ΔλRL,Δc1为例，其满足正态云分布C(0,0.053 6,0.005 4)，利用正向云发生器，取抽样次数为2 000，得到的误差分布如图6所示。

图6 满足正态云分布的转移率误差Fig.6 Transfer rate error under normal cloud distribution

通过场景削减技术最终得到27个典型场景，选取出现概率为85%的场景做算例分析，此时系统出力情况如附图4所示。算例4的系统总运行成本较算例3而言更高，其原因一方面是由于应对新能源出力不确定性而增加的备用成本；另一方面是因源荷双侧出力不确定性有可能导致的更为严重的弃电。

附图4 算例4仿真结果App.Fig.4 Simulation results of Case 4

对于新能源出力不确定性，若将系统备用约束被满足的概率提升至85%，则新能源发电对应的鲁棒成本Γt= 2.904 6，此时系统总运行成本增加至23 608元。类似地，若考虑新能源出力的最大波动范围为±40%，则系统总运行成本增加至24 248元。以上两种情况增加的主要成本均为备用成本，即为了应对更高的新能源出力不确定性，需要更多的备用容量。

对于负荷不确定性，考虑正态云分布的转移率误差，其本质是引入了转移率误差边界的误差。分别对比发生概率为74%、85%及94%下的场景，其实际负荷曲线如图7所示。

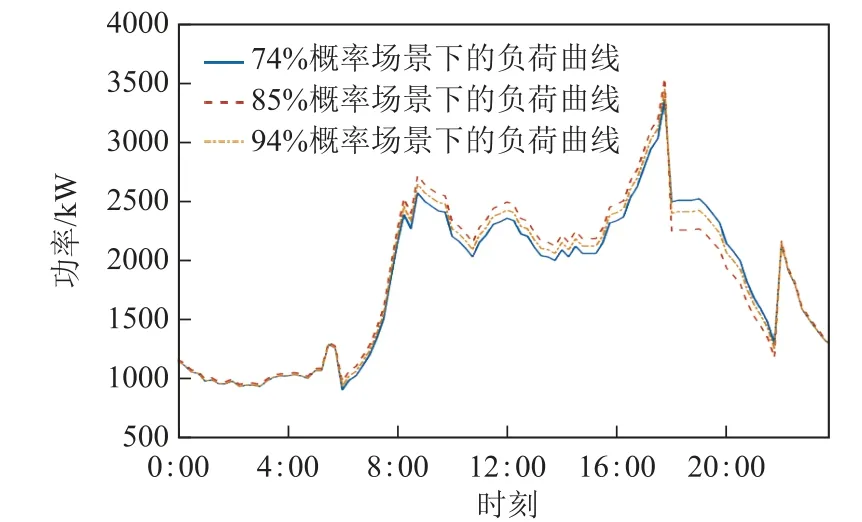
图7 不同概率场景下转移后的系统总负荷曲线Fig.7 System load curve in different probability scenarios

由图6和图7可知，场景发生概率与可转移负荷的转移量之间并无明显的正相关或负相关性。不同的概率分布对应于正态云分布式中的某个状态，概率越高，则当前状态附近分布式的点则越密集。在同一概率下，转移率误差边界同时存在上偏差和下偏差，因此难以仅从场景发生概率推断出负荷转移量的大小关系。通过若干典型场景的多次仿真计算，可描述出绝大多数情况下考虑负荷不确定性时的优化调度结果。

5 结论

本文针对多能源系统，提出一种基于广义储能的鲁棒优化调度策略。首先采用热电联供的能源集线器架构，对系统各实体单元进行建模。同时引入虚拟储能，分别采用正态云模型和自回归滑动平均时间序列模型对电、热柔性负荷进行建模，并由此对广义储能资源的调节特性进行了归纳。进而分别采用可调节鲁棒优化方法和多场景优化技术对系统源荷双侧不确定性进行了描述，建立了多能源系统不确定优化调度模型。最后采用鲁棒对等转换和多场景生成技术对模型进行了求解。算例结果表明，相对于常规储能，广义储能可以进一步发挥储能的灵活调节作用，充分利用系统各类调控资源。同时源荷双侧的不确定性不仅影响系统调度结果，还会增加系统备用成本。此外，在多能源系统中引入电转热装置，可增强系统内部热-电转换能力，提高新能源消纳水平。

附 录

附图2 算例2仿真结果App.Fig.2 Simulation results of Case 2

附图3 算例3仿真结果App.Fig.3 Simulation results of Case 3