基于运动粒子的粒子群目标跟踪算法

2021-09-16苏成志温迎晨张小忱王恩国

科技创新与应用 2021年25期

刘博，苏成志，温迎晨，张小忱，王恩国*

（1.长春理工大学机电工程学院，吉林长春130022；2.长春理工大学人工智能研究院，吉林长春130022）

目标跟踪是机器视觉领域中比较重要和热门的研究方向，也是各种视频应用中的一个基本任务。目标跟踪是指对视频序列中的运动目标进行跟踪，即通过给定第一帧的目标位置预测目标在后续视频序列中的位置[1]。目标跟踪在无人驾驶、无人机监测、水上智能监控、视频监控、数据检索、医学治疗以及军事侦察等诸多领域有着广泛的应用[2-5]，存在很高的应用价值和广阔的应用前景。

在目标跟踪领域，Isard首先提出CONDENSATION算法并利用粒子滤波算法解决目标跟踪问题[6]。经典粒子滤波算法容易实现且简单有效，对噪声干扰和目标遮挡具有较强的处理能力，但粒子滤波算法在目标遮挡情况下跟踪精度降低，并且存在计算量大和实时性不好等问题[7-10]。近年来，随着深度学习和卷积网络的飞速发展，Seunghoon等人[11]通过使用卷积神经网络学习辨别显著性图提出在线视觉跟踪算法，提高了准确度。Heng等人[12]提出利用循环神经网络（RNNs）对目标结构进行建模，采用级联策略融合CNN与RNN，提高了鲁棒性。由于深度学习的深层结构，计算复杂度高，导致很难达到实时跟踪的要求。

针对以上算法存在的不能兼顾目标跟踪时的处理速度与准确性的问题，本文另提出一种基于运动粒子的粒子群目标跟踪算法。该算法首先提取目标的HSV特征得到目标特征向量；然后为了提高跟踪的准确度在跟踪点周围撒下n个粒子构成粒子群，用梯度收敛算法来找到粒子群中单个粒子的最优解和粒子群的最优解，以种群的最优解作为下帧跟踪的跟踪点进行目标的跟踪。

1 提取目标HSV特征

在跟踪过程中，目标模型的建立可以为后续跟踪提供数据支撑，因此针对跟踪目标建立模型是目标跟踪算法首先要解决的问题。直方图作为一种经典统计模型，具有计算简便且易于实现的特点，广泛应用于机器视觉领域，是一种很好的图像特征表示手段。本文算法在首帧图像中选取所要进行跟踪的目标区域（通常为矩形窗口），以窗口中心为跟踪点，对目标区域进行直方图统计建立目标特征模型，从而得到目标特征向量。

1.1 建立HSV颜色特征模型

RGB模型作为应用最广泛的彩色模型，虽然能很好地吻合人眼强烈感知红、绿、蓝三原色的事实，但不适用颜色的直观描述；HSV模型采用色调（Hue）、饱和度（Saturation）和明度（Value）来描述物体，更符合于人类视觉的直观感受。相较于RGB模型，HSV模型各个通道的相关性较小。因此，本文算法通过提取HSV特征得到目标特征向量。

如图1所示，将图像由RGB模型转为HSV模型进行描述。为方便伪彩色显示，对HSV三通道取值范围进行量化处理，将取值区间由[0，360]、[0，1]和[0，1]分别拉伸或者压缩至区间[0，255]。由于V通道对光照变化非常敏感，为了尽量减少明暗变化的影响，在对目标建立颜色特征模型过程中，仅针对H通道和S通道建立直方图模型。

图1 HSV模型的伪彩色显示

如图2所示，首先对从源图像划分的目标区域分别建立H直方图模型和S直方图模型；假设目标区域中共有N个像素，第i个像素点的坐标为（xi，y）i，则第i个像素点的H通道信息为H（xi，y）i，S通道信息为S（xi，y）i。由于经过量化处理后H和S通道数据的取值范围均为0~255，为尽可能将数据离散化和方便统计，将直方图组数（Bins）设置为128。通过式（1）和式（2）计算可得H直方图模型H={Hu}和S直方图模型S={Su}。

图2 提取颜色特征模型

其中：如式（3）所示，δ为克罗内克函数（Kronecker delta）；u=0，1，…，127；w为目标区域宽度；h为目标区域高度。

1.2 目标特征向量

通过上述方法得到HSV颜色特征模型后，然后对H直方图模型和S直方图模型进行串联处理，如式（4）所示，便可得到目标特征向量C=（C0，C1，...，C127），C0~C63为H通道统计信息，C64~C127为S通道统计信息。

其中：Hu是H直方图模型，Su是S直方图模型，u=0，1，…，127。

1.3 特征提取的快速算法

1.3.1 快速算法的原理

在提取特征时，本文在原有特征提取的基础上提出一种快速算法。如图3所示，当粒子P的特征提取完后，对运动位置M2进行特征提取时，由于M2是P向上移动一行像素，只有首行像素是新信息，因此只需要在P特征提取信息的基础上添加M2首行信息，删除P最后一行的无用统计信息，这样就能得到运动位置M2的特征提取信息。

图3 快速算法

同理依次对M3、M5、M8、M7、M6、M4、M1运动位置的特征提取信息进行处理，就可以得到粒子P所有邻近位置的特征向量。

1.3.2 快速算法的优势

从算法原理可知该算法通过重复利用已知区域信息，可以很大程度上减小计算量，提高算法效率，如式（5）所示。

其中：v为快速算法对传统算法的倍数，w为目标区域宽度，h为目标区域高度。该快速算法与传统特征提取算法相比，在边长为5的正方形区域内提高了3.5倍，而宽度30，高度70的目标区域，提高了7.7倍。由此可知，当目标区域越大时，该算法的提升速率越高。

现在已经得到了目标特征向量，接下来先撒下n个粒子，然后通过以目标特征向量为核心的梯度收敛算法使每个粒子进行收敛运动。

2 结合梯度收敛算法的粒子群算法

首帧图像提取HSV特征得到目标特征向量后，在下一帧图像中，首先，通过粒子群算法在跟踪点周围撒下n个粒子，以此来增加算法的准确度；然后，通过梯度收敛算法寻找单个粒子的最优解和整个粒子群的最优解，单个粒子的最优解称为个体极值，整个粒子群的最优解称为全局极值。用全局极值更新跟踪点的坐标，进行下一帧的跟踪。

2.1 粒子群分布

本文根据式（6）在跟踪点周围撒下n个粒子形成粒子群，其中撒下的粒子中距离跟踪点越近粒子数越多，在目标跟踪过程中，当相似因子ε较小时，为了更好地跟踪目标，本文采用扩大粒子群分布区域的方法，该方法通过式（7）建立相似因子ε和σ的函数关系来控制分布区域的大小。

如图4所示，图中的白色矩形框为目标区域，（a）图为目标未被遮挡的跟踪效果图，此时粒子群分布都收敛到一个区域；（b）图为目标被遮挡时的跟踪效果图，为了能够重新找到目标，此时的粒子群分布发散。

图4 粒子群分布变化

2.2 寻找个体和全局极值的梯度收敛算法

2.2.1 相似因子ε

相似因子用来表征搜索区域与目标区域的相似程度。如图5所示，假设粒子P为粒子群中的某一粒子，5行5列的正方形区域为粒子的窗口区域，在某一帧图像中粒子P除了停止运动外，有8个运动方向分别为：M1、M2、M3、M4、M5、M6、M7、M8。

图5 单粒子移动

对当前位置窗口区域和邻近的8个区域进行特征向量提取，可以得到当前位置窗口区域的特征向量S0和邻近的8个区域的特征向量S1、S2、S3、S4、S5、S6、S7、S8。通过式（8）对当前位置窗口区域和邻近的8个区域进行相关性计算，得到当前位置窗口区域的相似因子ε0和邻近的8个区域的相似因子 ε1、ε2、ε3、ε4、ε5、ε6、ε7、ε8。

其中0≤ε<1，ε值越大，与目标区域相似程度越大，该区域为目标区域的可能性越大，反之可能性越小。

2.2.2 梯度收敛算法

单粒子的运动采用梯度下降法不断沿着相似因子梯度最大的方向进行运动直至收敛。

如图6所示，假设粒子P当前位置（像素坐标）为（x0，y）0，通过式（8）得到粒子P周围位置及当前位置的相似因子后，通过式（9）计算梯度信息，与像素坐标信息构成三元组（x，y，g），得到信息集合A={ai|ai=（xi，yi，g）i，0≤i≤8}。

图6 位置梯度信息三元组

利用式（10）计算得出g最大的三元组信息，并利用其中的像素坐标信息更新P粒子的像素坐标，则P粒子向g最大的位置运动；若当前位置的g最大，即g=0为最大值，则P粒子收敛。

当所有粒子完成收敛运动后，此时的所有粒子并不一定都收敛到同一位置，比较所有收敛位置的相似因子，将相似因子最大的位置作为下帧跟踪的跟踪点。

3 实验与分析

3.1 实验过程及中间结果

3.1.1 粒子群的分布结果

粒子群分布情况如图7所示，圆为目标跟踪点，黑点是分布的每个粒子。由图7可知，粒子的分布与前面的描述相同，离跟踪点越近粒子数越多。

图7 粒子分布

3.1.2 粒子群的运动

任取一帧图像，单个粒子单步运动过程及结果如图8所示，其中（46，48）是粒子P的坐标位置，Col表示当前位置的相似因子大小，（46，49）坐标位置对应图5的M2位置，可知M2位置的相似因子最大，因此粒子P向M2位置运动，下一步以M2为中心点，继续判断粒子的运动方向。

图8 单粒子运动轨迹

所有粒子的总体运动轨迹及结果如图9所示，图中小圆是上帧图像的目标点，每个黑点代表一个粒子，黑色线是粒子进行收敛运动的轨迹，三角形是粒子收敛后的位置，Col是相似因子的大小。从图9中可以看到最终收敛到三个位置，比较这三个位置的相似因子，将相似因子最大的位置作为下帧跟踪的跟踪点。

图9 所有粒子运动轨迹

3.2 实验分析

为了评估算法性能，先从速度、准确度两个角度与CSK、KCF、MS、CPF、Struck、DFT算法进行实验对比，然后从兼顾速度与准确度角度与其他算法进行跟踪性能评价，本算法在实验过程中以Ours命名。

如表1所示，在OTB2013中选取5组彩色序列作为测试序列，所有算法保持原有参数不变。计算机硬件配置为Inter Core i7 CPU，内存8G，实验平台环境为Matlab 2016b。

表1 实验的视频序列

3.2.1 速度分析

各个算法对OTB2013中选取的5组实验序列的处理速度结果如表2所示，表中数据单位为帧/秒，其中Av列为各个算法对5组视频序列的平均处理速度，计算公式如式（11）所示。

表2 不同跟踪算法的处理速度

从Av列数据可知，本文算法处理速度为199.0帧/秒，比CSK慢了1.54倍，与MS算法比较接近，而其他算法皆低于本文算法。

3.2.2 准确度分析

为评估算法的准确度，本次实验使用OPE（One Pass Evaluation）模式，采用中心位置误差标准作为评价标准，绘制精确度曲线（precision plot）。其中，如式（12）所示，中心位置误差P是指算法的目标中心位置（xr，y）r和真实目标中心位置（xs，y）s的平均欧式距离值。精确度描述的是给定的中心位置误差阈值之内跟踪正确的帧数占总帧数的比例，本次实验采用的阈值为20个像素。

如图10所示，在实验的7种算法中，本文算法精确度最高为0.790，高出CSK1.52倍、高出MS1.57倍。为更直观地评估算法的跟踪性能，选取精确度前五的算法在Couple、Doll和Lemming三组序列下的运行结果。

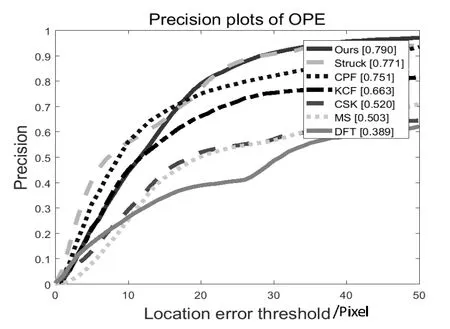
图10 OPE精确度对比曲线

如图11所示，在第18帧中CSK算法脱离目标；在第36帧中KCF算法脱离目标；在第92帧中CPF算法和Struck算法都脱离目标，只有本文算法能一直有效地跟踪目标。

图11 Couple序列部分跟踪结果

如图12所示，在第1628帧中CSK算法脱离目标；在第3750帧中CPF算法偏离目标；在第3774帧中Struck算法脱离目标，CPF算法重新找到目标，本文算法和KCF始终附着在目标上。

图12 Doll序列部分跟踪结果

如图13所示，在第388帧中当目标被遮挡再次出现时，KCF算法脱离目标；第885帧中CSK算法脱离目标，当目标未被遮挡地运动到KCF算法丢失目标的位置时，KCF算法重新找到目标；第970帧中Struck算法脱离目标，本文算法和CPF算法一直稳定地跟踪目标。从该序列跟踪过程可知该算法可以克服目标短暂遮挡问题。