基于数学学科核心素养的普通高中数学教科书与课程标准比较分析——以人教A版中的“函数”习题为例

王彦棋,石玲瑜,2

(1.贵州师范大学 数学科学学院,贵州 贵安新区 550025;2.怀化师范高等专科学校 小学教育学院,湖南 怀化 418000)

国家课程标准是教材编写、教学、评估和考试命题的依据,是国家管理和评价课程的基础[1].近年来,随着国家课程标准的不断改革,核心素养一词逐渐出现在人们的视野里,并成为教育界研究的热点话题.具体到数学学科而言,《普通高中数学课程标准(2017年版)》[以下简称《课程标准(2017年版)》]将数学学科核心素养定义为它是数学课程目标的集中体现,是具有数学基本特征的思维品质、关键能力以及情感、态度与价值观的综合体现,是在数学学习和应用的过程中逐步形成和发展的[2],具体包括数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析六大核心素养.通过查阅相关文献发现,《课程标准(2017年版)》作为高考的重要风向标,在核心素养一词被正式提出后,有关数学核心素养测评的研究就如雨后春笋般逐渐涌现出来.比如,李爽等[3]借助喻平的数学核心素养评价指标框架建立了高中数学核心素养评价指标体系,分别对2012年和2018年全国高考文理科数学Ⅲ卷和云南高中学业水平考试的数学试卷进行分析,认为2012年和2018年各3份测评试卷对各素养考查年度平均权重分布无明显差异,间隔5年的考卷对数学核心素养的考查总体变化不大;张玉环等[4]在核心素养评价框架的基础上,采用多元统计的方法分析2015-2019年的中法高考试题,并从核心素养的视角提出高考命题建议;李华等[5]结合喻平的数学核心素养评价框架,进一步改进李作滨、朱先东等的研究工作,采用多元统计方法对2019年高考数学全国卷进行了定性与定量分析,并给出相应的建议;覃创等[6]在李华等人的研究基础上,结合各部分学习的比重,以2020年全国I卷为例来分析数学核心素养的具体落实情况;朱立明[7]在其构建的“主题内容×素养成分×观测指标”数学学科三维测评框架的基础上,以定量分析的方法对2020年数学新高考I卷中考核的数学内容进行分析.上述研究都是以高考试卷为例来分析数学核心素养的具体落实情况,关于数学学科核心素养在教材与课程标准的一致性表现的分析研究却微乎其微.而教材是课程标准的理念、目标和内容的具体体现,是直接指导课程实施的潜在实施课程[1].数学习题作为数学教材的重要组成部分,是数学教学过程中组织学生学习、实践活动的一种重要形式[8],所以有必要从数学学科核心素养的角度出发,对比分析其在课程标准与数学教科书中的具体体现.

基于此,本研究以2019年教育部审定的人民教育出版社A版普通高中数学教科书中“函数”部分的习题为研究对象,以喻平的数学核心素养评价框架为研究工具[9],对比分析五大数学核心素养(因“函数”内容几乎不涉及数据分析素养,故将其去除)在课程标准与人教A版普通高中数学教科书“函数”内容习题部分的具体体现,以期对今后我国高中数学新教材与课程标准的编写与修订提供一定的参考建议.

1 研究设计

数学学科核心素养是在《课程标准(2017年版)》中被具体提出的,而最新版的普通高中数学教科书就是以《课程标准(2017年版)》为依据编制而成的.因此,对比分析研究数学学科核心素养在课程标准与现行最新版教材中的具体体现以及如何体现,对今后教材的编写与修订都具有重要的意义.

1.1 研究对象

考虑到现行最新版数学教科书的使用分布情况,本研究选取2019年教育部审定的人民教育出版社A版普通高中数学教科书必修第一册和选择性必修第二册中“函数”部分的课后习题为研究对象,主要包括“练习”“习题”以及“复习参考题”中的所有题目.

1.2 评价框架和指标体系的确定

想要研究数学学科核心素养在教材习题中的具体体现,就需要有一套科学、合理的核心素养水平划分标准.喻平从知识的角度出发,以布鲁姆的学习目标分类、PISA模型和SOLO模型为参考依据,提出了一种划分标准:将知识学习分为知识理解、知识迁移和知识创新三种不同的形态,每一种形态对应数学学科核心素养的三种不同层次的水平,并依次给出了进一步的解释[9].由此,就给数学学科核心素养的评价提供了一个评价框架(见表1).

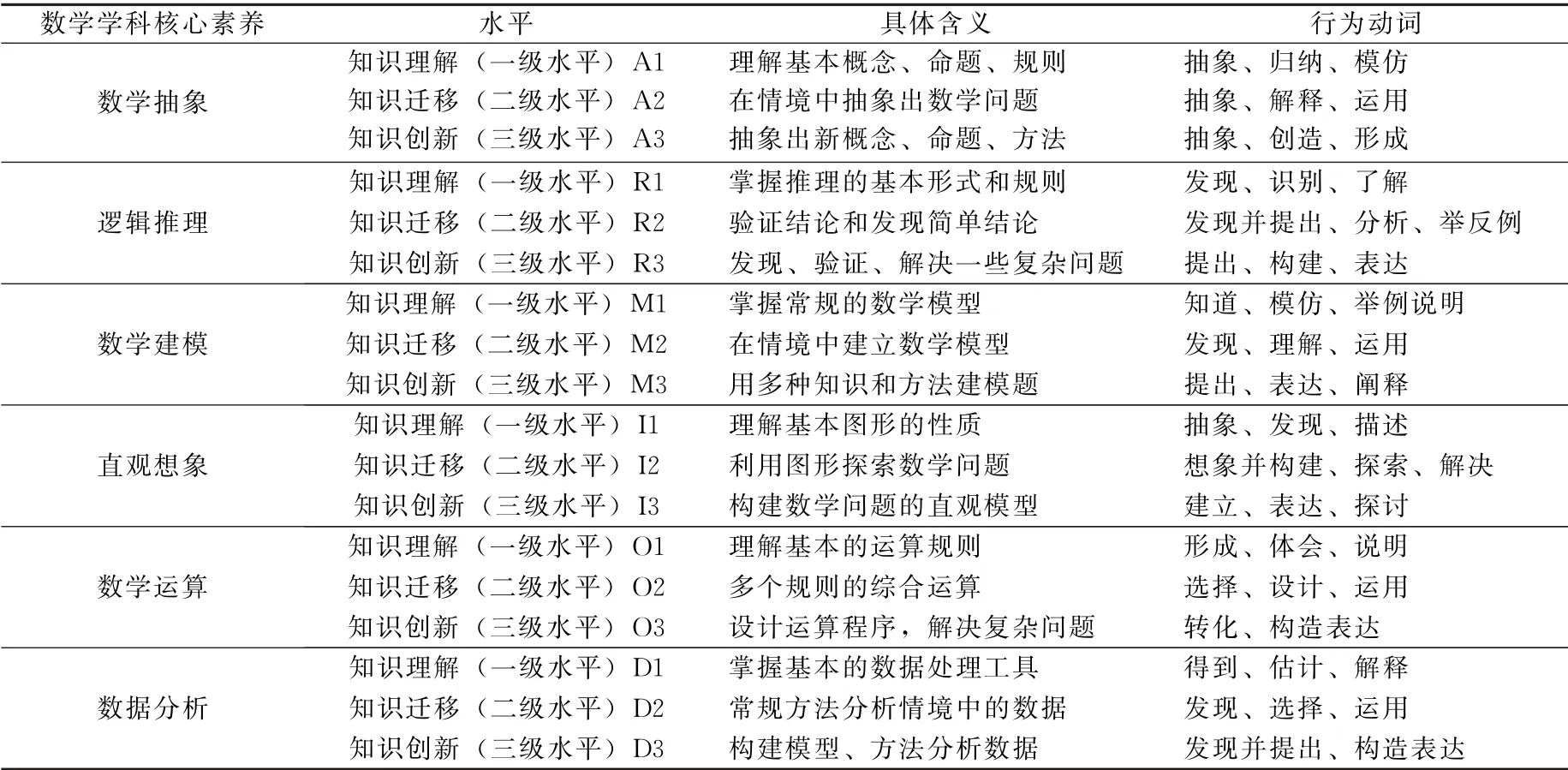
表1 数学学科核心素养评价指标框架[9]

1.3 编码方法

为方便统计与分析,将普通高中数学教科书与《课程标准(2017年版》中的“函数”部分的课程内容进行编码.首先,用BX、XX来区分课标中的必修与选择性必修两部分内容,对于“函数”主题的每一单元用HS1、HS2、HS3、…等方法表示,每一单元的具体目标则用1-1、1-2、1-3、…等方法表示.而核心素养水平划分则按照表1中介绍的框架,用字母A、R、M、I、O分别表示数学抽象、逻辑推理、数学建模、直观想象、数学运算这五个数学核心素养(因“函数”内容几乎不涉及数据分析素养,故将其去除);用数字1、2、3分别表示一级水平、二级水平和三级水平.例如:BX1-HS1-1-2-A2表示必修课程的“函数”主题这条主线中“函数概念与性质”的第二条,具体描述内容属于数学抽象素养,水平划分为知识迁移二级水平.

人教A版普通高中数学教科书中习题的编码方法与《课程标准(2017年版)》编码方法类似,首先需要分析教材习题中所包含的知识点,然后判断其中蕴含的数学学科核心素养,并根据出题意图中的行为动词进行相应的水平划分.例如,求下列各式的值:(1)log525;此题需要学生理解基本的运算规则,归为数学运算素养的水平一,编码为:O1.需要注意的是,每一道习题有可能蕴含不止一个数学核心素养,因此在编码时需要根据具体题目将其归于最能体现该内容的数学学科核心素养水平之内,使得每条内容和习题最多对应两个数学学科核心素养、一个水平层次.例如:一枚炮弹发射后,经过26 s落到地面击中目标.炮弹的射高为845 m,且炮弹距地面的高度为h(单位:m)与时间t(单位:s)的关系为h=130t-5t2,求其所表示的“函数”的定义域与值域,并用“函数”的定义描述.此题需要学生理解“函数”的概念并能进行解释,同时需要求出“函数”的定义域与值域,所以,此题考查了数学抽象和数学运算两个核心素养,前者对应认知水平二,后者对应认知水平一.由此,可将此题编码为:A1/O1.

1.4 编码检验与数据统计

本研究的编码过程是由两名研究者在共同学习研读了《课程标准(2017年版)》与喻平教授的数学学科核心素养评价框架后分别独立完成,整个过程保持了高度统一的标准.为了检验编码的可靠性,利用SPSS22.0软件对编码进行了内部一致性检验,得到课标与习题编码的克隆巴赫系数分别为0.946、0.934,说明编码具有较好的内部一致性.在此基础上,对编码存在差别的地方进行了讨论与修订,由此确定了编码的最终版本.得到的编码结果见表2和表3.

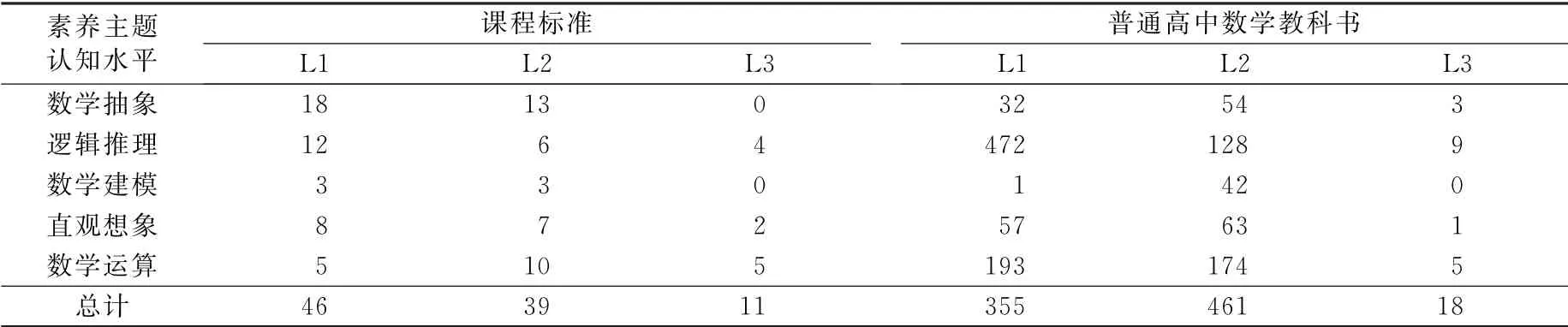
表2 《课程标准(2017年版)》与人教A版普通高中数学教科书频数统计

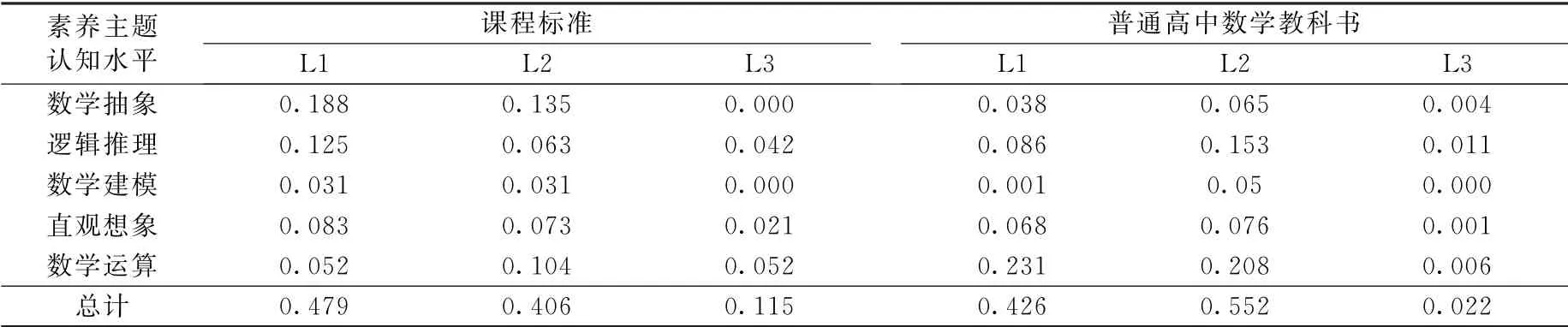
表3 课程标准(2017年版)》与人教A版普通高中数学教科书频率统计

2 研究结果分析

2.1 人教A版普通高中数学教科书习题与《课程标准(2017年版)》的一致性

将表2和表3分别看作两个频数矩阵和比例矩阵,借助帕特等人的一致性系数公式[10]

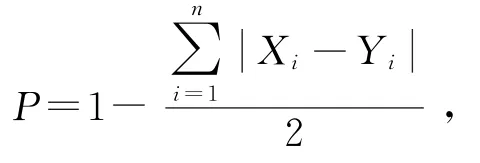
分析人教A版普通高中数学教科书习题与《课程标准(2017年版)》的一致性.其中:n代表矩阵的单元格个数,X i、Y i分别代表两个矩阵中第i个单元格的数值,P值表示一致性系数,P值越大,说明二者的一致性程度越高.将数据代入公式进行计算,得到人教A版普通高中数学教科书“函数”内容习题与《课程标准(2017年版)》之间的一致性系数为0.6,说明二者之间在一定程度上具有一致性,但是不具有统计学上的意义.

2.2 数学学科核心素养在人教A版普通高中数学教科书习题中的体现情况

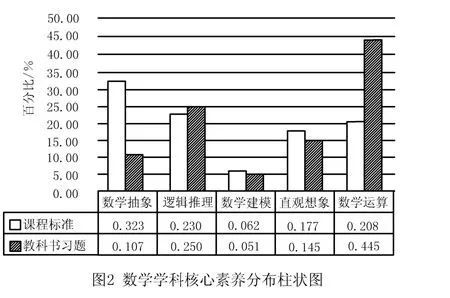
从图1可以看出,人教A版普通高中数学教科书“函数”部分的习题在内容结构上主要测查学生的数学抽象、逻辑推理、数学建模、直观想象与数学运算五大数学学科核心素养,这与“函数”知识本身的性质有关.可以看出,各个素养的测查分布情况并不均衡,《课程标准(2017年版)》对学生在学习“函数”部分内容时需要形成的数学抽象素养要求更高,但是人教A版普通高中数学教科书在这部分的测查仍然更倾向于学生数学运算素养的形成.若将《课程标准(2017年版)》作为比较标准,可以将教科书中的习题分为三种类型,即超标型、符合型和不足型[11].从图2可以具体看出,在人教A版普通高中数学教科书“函数”内容习题中数学运算素养属于超标型,其测查超出《课程标准(2017年版)》的23.7%.将相差不足3%的归属于符合型,则逻辑推理和数学建模属于符合型,即符合《课程标准(2017年版)》的要求.数学抽象与直观想象属于不足型,其测查情况分别低于《课程标准(2017年版)》的21.6%、3.2%,数学抽象素养的测查相差较大.

2.3 人教A版普通高中数学教科书对认知水平的测查情况

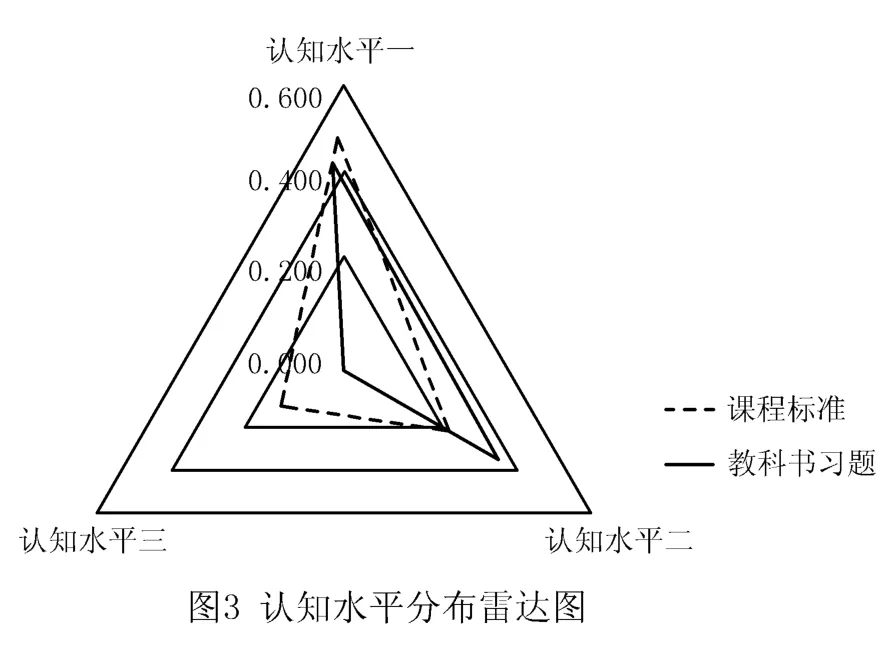
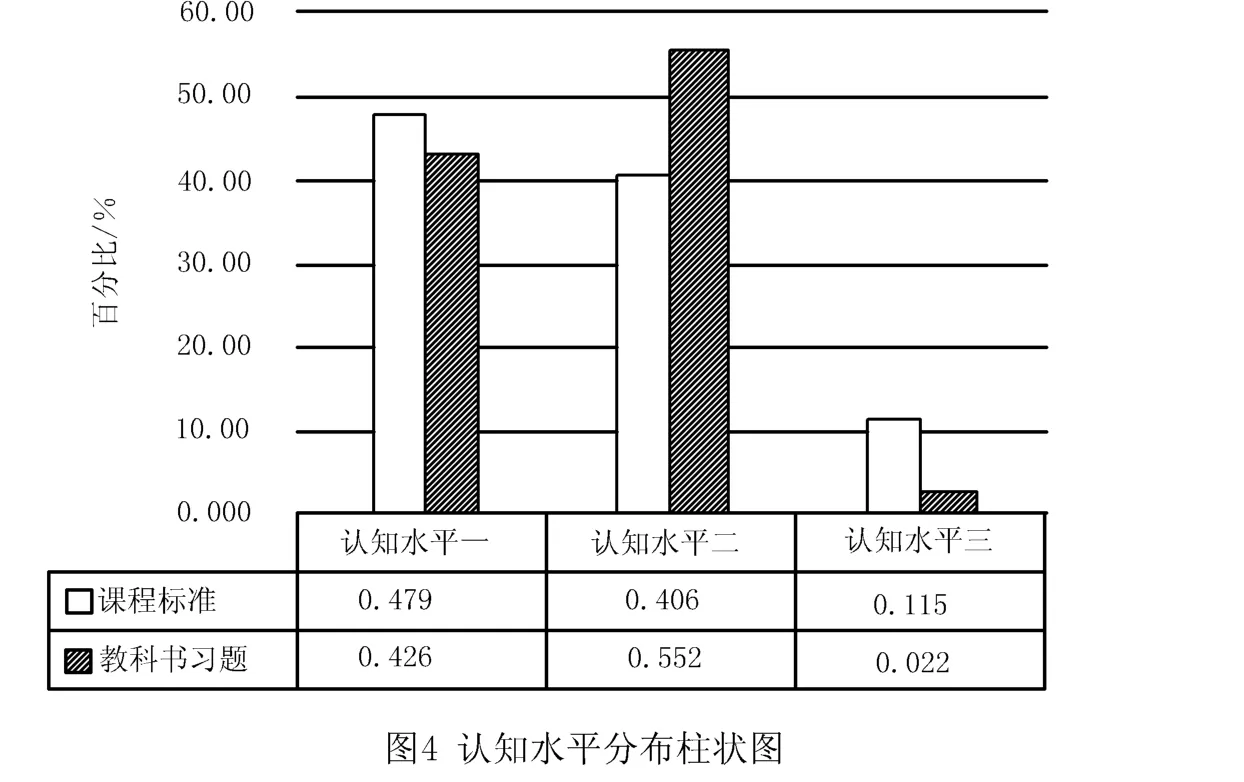
从图3可以看出,人教A版普通高中数学教科书“函数”内容习题对数学内容的测查与《课程标准(2017年版)》的要求大体上相差不大,其测查主要集中在水平一与水平二.由图4可以具体看出,教科书对认知水平一的测查与《课程标准(2017年版)》的要求一致性程度最高,仅相差5.3%,对认知水平二的测查则超出了《课程标准(2017年版)》要求的14.6%,而对于认知水平三的测查低于《课程标准(2017年版)》的9.3%.总体来看,人教A版普通高中数学教科书“函数”部分内容的课后习题整体处于中等水平,大体符合《课程标准(2017年版)》的要求.

2.4 数学学科核心素养各水平在人教A版普通高中数学教科书习题中的具体体现情况

由图5可知,在人教A版普通高中数学教科书“函数”主题部分,数学学科核心素养各水平总体在《课程标准(2017年版)》要求的水平上下波动.可以看出,数学抽象、逻辑推理以及数学建模的测查主要集中在水平二,所占比例分别为6.5%、15.3%、5%,其中逻辑推理与数学建模该水平的测查均高于《课程标准(2017年版)》的要求,数学抽象该水平的测查则远低于《课程标准(2017年版)》的要求,三者水平一的测查也均低于《课程标准(2017年版)》的要求.直观想象与数学运算的测查主要集中在水平一和水平二,直观想象水平一与水平二所占比例依次为6.8%、7.6%,数学运算水平一与水平二所占比例依次为23.1%、20.8%,除了直观想象的水平一低于《课程标准(2017年版)》的要求,二者其余水平的测查均高于《课程标准(2017年版)》的要求.在五个数学学科核心素养中,对于水平三,在人教A版普通高中数学教科书“函数”部分除了数学抽象与数学建模并未测查,其余三者的测查均低于《课程标准(2017年版)》的要求.

3 研究结论与建议

3.1 研究结论

首先,借助帕特等人的一致性系数公式对编码数据进行计算,得出人教A版普通高中数学教科书“函数”内容习题与《课程标准(2017年版)》在一定程度上存在一致性,但是不具有统计学上的意义,整体表现一般.其次,通过对数据进行详细分析可以看出,虽然人教A版普通高中数学教科书在“函数”部分已经参照了数学学科核心素养,并且在一定程度上对各个核心素养及其不同水平都进行了测查,且整体处于中等水平,但是距离《课程标准(2017年版)》的要求还存在一定的差距.即使《课程标准(2017年版)》对“函数”内容主题的要求是重点突出培养学生的数学抽象素养,但人教A版普通高中数学教科书“函数”内容习题依旧受应试教育的影响,更加倾向于学生数学运算素养的培养,这也是今后新教材修订与完善需要注意的地方.

3.2 建议

3.2.1 围绕课标要求,综合提高核心素养测查的平衡性

教科书正文内容无疑需要体现数学核心素养的课程目标要求,而习题作为教科书正文内容的进一步巩固和发展,也需要体现数学核心素养的课程目标要求[12].由图1、图2可知,数学学科核心素养在人教A版普通高中数学教科书“函数”内容习题的分布排列情况并不均衡,其对学生数学运算素养的培养尤其突出,这与《课程标准(2017年版)》重点强调培养学生数学抽象素养的要求并不一致.究其原因,可能与长期以来的应试教育有关,这并不利于学生学习能力的全面发展.课后习题不应仅仅被认为是评估、诊断以及学生练习巩固的工具,它也应是促进学生核心素养全面形成的“催化剂”.因此,基于核心素养的教科书编写,应紧紧围绕课标要求,综合提高核心素养测查的平衡性,使学生各个核心素养的形成均衡.

3.2.2 把握数学本质,适当增加高级认知水平的权重

美国国家数学咨询委员会在2008年颁布的总结报告《成功需要基础》中,特别强调高水平的认知能力对提高国家竞争力、国民素养及生活水平的重要性[1].然而,通过上述研究以及结合平时的经历可以发现,无论是课程标准还是教科书习题,都过于注重学生对知识的“理解”与“运用”等中低级认知水平,较少关注学生“探索”“创新”等高级认知水平与能力的培养,这与《课程标准(2017年版)》中提出的培育学生科学精神和创新意识的理念不相一致.因此,今后教科书习题的编写应当以学生为本,在把握数学本质、关注学生发展的基础上,适当增加习题难度与创新性,从而加大高级认知水平的权重,由此尽可能地落实数学教育立德树人根本任务,发挥数学课程发展学生素质教育的功能.