无人机激光相对引导系统设计与试飞验证

李 晖，杨朝旭，唐 勇，马 波，倪 静

（1.航空工业成都飞机设计研究所，成都 610091；2.歼击机综合仿真航空科技重点实验室，成都 610091）

目前军事上和工业上常用的无人机，按照结构设计与翼型来划分，可分为固定翼无人机和旋翼无人机[1]。

固定翼无人机在各国军队中占绝大多数，典型型号有美国的“琥珀”（Amber）、“先锋”（Pioneer）、“扫描鹰”（Scan eagle）等。小型固定翼无人机普遍采用的回收方式有：撞网回收、伞降回收、撞绳回收、轮式滑跑回收等[2⁃3]。撞网回收、伞降回收对回收精度要求较低，但对无人机机体会造成一定的损伤。撞绳回收方式在“扫描鹰”无人机系统得到应用，利用翼尖钩钩住绳索完成无人机回收操作，这种方式对无人机机体损伤较少，但对回收定位精度要求很高。轮式滑跑回收对无人机损伤最小，但对回收场地和引导精度要求较高。

针对轮式滑跑着陆回收方式，无人机着陆引导主要手段有卫星、雷达、视觉和激光相对引导等[4⁃5]。激光具有高亮度、高方向性、高单色性和高相干性4 大特性。因此相较于雷达引导和视觉引导，激光相对引导具有抗干扰能力强，精度高，白天夜晚都可以工作等优点，激光相对引导成为研究热点。同时，激光的发散角小，能量集中，能够实现极高的探测灵敏度和分辨率；其波长使得天线和系统尺寸可以很小，这些是传统雷达不可比的。激光相对引导技术综合了激光器技术、光子探测技术、信号处理技术等多项技术，测距精度高、测程大、可靠性高，能够满足目标高精度、大测程测距的要求。

激光相对引导技术[6⁃7]在军事领域中已有广泛的应用，美国、俄罗斯、日本和瑞士等国均对激光相对引导技术有着深入的研究和应用。其中，美国、俄罗斯和日本等国将激光引导技术应用于航天器空间交会对接，在数公里至数米的中、近距离实现目标飞行器的捕获、跟踪和测量。基于相同的原理，在无人机着陆时，高精度可靠的激光相对引导系统能够在视场范围内可自主进行扫描，捕获与跟踪，并进行实时测量，将测量三维数据回传至飞行器，引导其进行着陆。瑞士的RUAG 无人机相对引导着陆系统是激光相对引导技术的典型应用案例，可在约4 km 距离实现±1.5 m 探测精度指标。在已有研究基础上，如何进一步在高精度完成激光相对引导系统的扫描、捕获、跟踪和测量工作，是激光相对引导系统研究的重点和难点。

本文在现有的研究基础上，搭建了激光相对引导系统，设计了基于激光引导的无人机着陆试验流程，并开展了实时测量试验。主要工作包括：

(1) 按照既定策略，通过激光引导系统的主机实现极短时间内既定空域的扫描；

(2) 将初始指向实现视轴初始对准与扫描捕获完成对捕获不确定区域覆盖结合，实现回波信息的提取；

(3) 采用粗精复合轴跟踪技术与高精度测距系统，从而克服跟踪过程中相对运动以及平台振动对视轴对准精度的影响，从而获得目标较高精度的角度和相对距离信息。

飞行试验结果表明，高速飞行的无人机能够实现较高精度的相对位置测量，激光相对引导技术可用于引导无人机下滑着陆过程。

1 激光相对引导系统基本工作原理

激光相对引导系统组成包括：激光相对引导系统主机和合作目标。其中主机安装在地面，合作目标安装在飞机上[8⁃9]。

激光相对引导系统工作过程主要分为：扫描、捕获、跟踪和测量。扫描指在相对距离范围内，首先通过激光引导系统主机按照既定的策略，在极短时间内实现激光束对既定空域内的快速覆盖；捕获分为两个过程：初始指向和扫描捕获。初始指向过程是根据外部姿态与位置数据解算后，驱动捕获机构实现视轴的初始对准。由于引导信息和机构指向精度均存在误差，系统存在捕获不确定区域。扫描捕获过程是按照规划的轨迹控制光轴（视轴）完成对捕获不确定区域（目标视场）的覆盖，直至在捕获视场内成功提取到回波信息。

跟踪过程主要克服相对运动和平台振动对视轴对准精度的影响，将视轴对准误差控制在允许的范围之内。采用高精度跟踪，通常需要采用粗精复合轴跟踪技术。

测量过程是在实现对目标高精度捕获跟踪后，通过复合轴的转向得到目标的角度信息，而相对距离值则由高精度的测距系统给出，从而获得目标的三维信息。

2 激光相对引导系统研制与试飞试验数据分析

通过对无人机着陆引导的总体需求分解，初步明确了激光相对引导技术的功能、性能、可靠性、安全性等需求，形成了基于激光相对引导的全自主、高精度、实时的着陆引导初步技术方案，开展了激光相对引导系统组成架构、工作原理、硬件设计、关键技术指标及接口等研究，完成了激光相对引导系统原理样机研制与实验室测试。

为了进一步验证激光相对引导系统的功能和性能，在西北某机场，在某无人机着陆过程中，开展了激光相对引导系统实时测量试验。如图1 所示，圆圈中的合作目标被固定在被测飞机的前机身进气道下侧；如图2 所示，激光相对引导系统主机放置在图中左下角跑道边缘蓝圈位置，箭头所示方向为飞机着陆后在跑道上的滑行方向。

图2 激光相对引导系统主机安装位置示意图Fig.2 Schematic diagram of installation position of laser rel⁃ative guidance system host

当主机接收到引导命令后，根据相关引导参数，以跑道中线为轴线进行N°×N°扫描，随后发现目标，捕获目标，转入跟踪。在空中，系统可完成无人机下滑道的全程稳定跟踪和数据输出；着陆后，完成从着陆点到刹停全过程稳定跟踪。从稳定跟踪开始，地面数据采集设备定周期的采集主机输出的方位、俯仰和距离。因为参考坐标系的差异，无法将激光相对引导系统测量数据与差分GPS 测量数据直接进行比较。因此，需要将两种测量体制的数据转化到相同的坐标系。

GPS 数据是基于WGS84 坐标系的，如图3 所示，Zw轴指向1984.0 定义的协议地球极(Conven⁃tional terrestrial pole, CTP)方向，即北极；Xw轴指向BIH 1984.0 的零子午面和CTP 赤道的交点，即零度经线方向；Yw轴与Zw轴、Xw轴垂直构成右手坐标系。

将激光相对引导系统主机放至在G点，能过GPS 测 出 基 经 度 为ag，纬 度 为bg，高 度 为hg，Xw绕Zw轴 旋 转-(90-ag)°转 化 为X′g；Zw绕X′g旋 转-(90-bg)°转 化 为Zg；X′g沿Zg平 移hg转 化 为Xg；Yg轴与Zg轴、Xg轴垂直构成右手坐标系，将此坐标系定义为地平坐标系。则WGS84 坐标系下任意一点(xw,yw,zw) 可转化为地平坐标系下的(xg,yg,zg)，其转化关系如下

如图4 所示，飞机在地面基准点P0时GPS 测出其WGS84 系下的坐标为(xw0,yw0,zw0)在飞行和滑行过程中某一时刻所在位置点P1，其WGS84 系下的坐标为(xw1,yw1,zw1)。通过上述公式(1)，可得到P0和P1在地平坐标系下的坐标(xg0,yg0,zg0)和(xg1,yg1,zg1)，其投影在XgYg平面上的点为P′0和P′1，其在地平坐标系下的坐标 (xg0,yg0,0) 和(xg1,yg1,0)。地平坐标系下主机放至点G的坐标为(0,0,0)。

图4 比对数据计算示意图Fig.4 Diagram of comparison data calculation

地平坐标系下矢量P′0的角度为βg0，其计算表达式如下

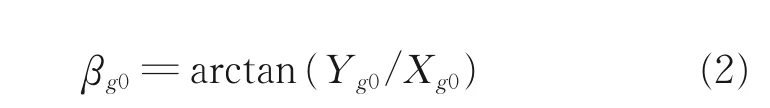
将激光相对引导系统主机放置在G点并调平，其坐标系定义如下：原点为G点，Zr轴指向天顶与Zg共线，Xr轴指向正前方，即激光相对引导系统主机0°方位角指向，Yr轴与Zr轴、Xr轴垂直构成右手坐标系，激光相对引导系统主机测量出的P0和P1的俯仰角为αr1和αr0，方位角为βr1和βr0，距离为ρr1和ρr0，通过计算可得出P1点在主机系下的坐标为(xr1,yr1,zr1)，计算方法如下

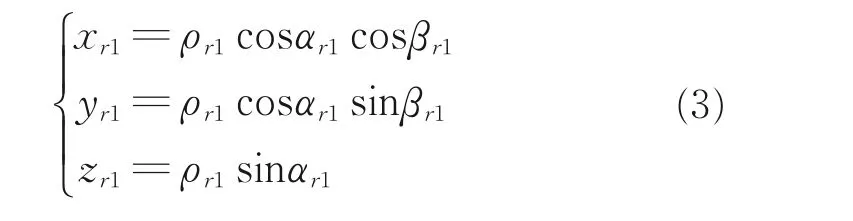
因为Zr与Zg共线，两个坐标系原点都为G，所以XrYr与XgYg共 面。Xr到Xg轴的角为Δβ，计算方法如下

将P1点主机系下的坐标(xr1,yr1,zr1)，绕Z轴旋转Δβ，得到其在地平系下的坐标(xrg1,yrg1,zrg1)，则

在地平坐标系下在Xg、Yg、Zg方向的误差分别为σX1、σY1、σZ1，计算方法如下

根据上述模型计算，得到地平系下的激光相对引导系统测量的数据(xrg1,yrg1,zrg1)和机载差分GPS 卫导系统测量的数据(xg1,yg1,zg1)。分别绘制两种体制测量数据X、Y、Z轴方向数据比较曲线，如图5～7 所示。

图5 在地平系下两种体制测量数据X 轴方向坐标比较Fig.5 Comparison of X⁃axis coordinates of two kinds of measurement data in horizontal system

图6 在地平系下两种体制测量数据Y 轴方向坐标比较Fig.6 Comparison of Y⁃axis coordinates of two kinds of measurement data in horizontal system

图7 在地平系下两种体制测量数据Z 轴方向坐标比较Fig.7 Comparison of Z⁃axis coordinates of two kinds of measurement data in horizontal system

从数据上看，从相距2 200 m 左右，激光相对引导系统主机即开始了对无人机的捕获和跟踪，跟踪全程稳定、未出现目标丢失现象。从数据曲线可以看出，两种测量体制的数据连续性和一致性较好，未出现数据丢失和幅值较大的野点。其中，测量过程中由于大气波动和无人机机载振动等的影响，两种体制测量数据在地平系下Y 轴方向存在高频低幅值抖动，经分析不影响使用。

在地平系下，以差分GPS 测量数据为基准，计算出激光相对引导系统主机测量的飞机坐标数据误差并绘制曲线，如图8 所示。

图8 在地平系下两种体制测量数据XYZ 轴误差比较曲线Fig.8 Error comparison curves of XYZ axis of two kinds of measurement data in horizontal system

从误差曲线可以看到，激光相对引导系统与差分GPS 测量数据在X、Y、Z轴方向的最大误差均小于1 m，测量误差的标准差如表1 所示。

表1 试验中两种体制X、Y、Z 轴方向误差的标准差Table 1 Standard deviation of XYZ axis error of two sys⁃tems in test m

通过本次无人机着陆试飞试验表明，激光相对引导系统与差分GPS 测量数据精度基本相当，具备发展成为一种无人机在卫星拒止环境下的备用测量手段。

虽然激光相对引导系统能够对高速飞行的无人机实现较高精度的相对位置测量，但实现工程应用还需要关注以下问题：

（1）需要积累更多试飞试验数据，满足各种着陆情况；

（2）需要进一步验证气象条件对激光相对引导系统作用距离、精度的影响；

（3）需要加强激光相对引导系统的人眼安全设计。

3 结 论

无人机回收是无人机飞行过程中的重要阶段，也是飞行事故的高发阶段，随着无人机在军事作战应用领域的不断扩大，无人机对安全回收的需求也日益凸显。尤其在卫星拒止条件下，激光相对引导技术基本不受无线电干扰的影响，可为无人机提供高精度的进场引导数据。本文对激光相对引导系统的工作原理及流程进行了分析，设计了基于激光引导的无人机着陆试验流程，并基于某无人机平台完成了试飞验证，获得了重要的试验数据，最后将激光相对引导数据与差分GPS 引导数据统一转换到地平坐标系下，完成了两种体制的数据比较和误差分析，试验结果表明激光相对引导技术稳定可靠、测量精度较高，可用于引导无人机下滑着陆过程。本项目所取得的所有技术，既可应用于我军陆基战术无人机、海基舰载战术无人机等军事应用领域，还可推广应用于船舶、兵器等领域的无人作战系统中。