涡扇发动机的一类大包线系统建模

凌彦聪，周文祥，朱平芳，曾建平

（1.厦门大学航空航天学院，厦门 361005；2.南京航空航天大学能源与动力学院，南京 210016）

非线性和时变是涡扇发动机系统中普遍存在的现象，高精度的非线性时变数学模型是涡扇发动机特性分析和综合的基础。早期涡扇发动机建模方法，大都采用线性化模型，未能真实地反映涡扇发动机系统时变和非线性的动态信息。针对这一问题，吴斌等［1］建立线性变参数（Linear parameter⁃varying，LPV）模型描述涡扇发动机大范围变化的动态特性，LPV 系统的系统参数可以表示为参数的函数，是基于状态的增量形式，需要与稳态基线模 型 结 合 使 用。Fu 等［2⁃3］提 出 一 类 能 够 描 述 对 象非线性和时变特性的非线性变参数（Nonlinear pa⁃rameter⁃varying，NPV）模型。该模型将非线性特性表征为依赖状态的多项式函数，其状态是基于对象的物理量，但由于其不需要基线模型则会带来误差的积累。因此，在拟合成NPV 模型之前如何高精度地对各个稳态点以及各包线的建模就显得至关重要。本文采用系统辨识的思想研究涡扇发动机的NPV 系统建模方法。

关于涡扇发动机模型辨识可以分为两类：一是对试验数据的辨识修正提高部件法模型的精度。二是选择输入输出数据以及模型类进行辨识建模。美国路易斯研究中心较早地研究系统辨识理论在发动机控制系统设计中的应用，Banazadeh等［4］提出一种扫频方法，通过发动机频域响应得到其 频 率 响 应 函 数。Kaufman 等［5］提 出GE7 燃 气 轮机建立状态变量模型的分步辨识方法。Breikin等［6］通过对发动机稳态点的输入输出数据，利用最小二乘法辨识状态空间系统矩阵参数得到发动机多变量的状态变量模型。Norton 等［7］研究不同的输入燃油信号对发动机时间序列模型辨识的影响，提出计算发动机时间序列模型参数的方法。As⁃gari 等［8］与郭政波等［9］提出NARMAX 模型利用正交分解法对发动机起动过程进行系统辨识，建立发动机非线性模型。随着航空发动机多变量控制规律研究的深入，国内也相应地展开涡扇发动机模型辨识领域的研究，姜锐［10］、吴斌［11］等学者采用正弦燃油信号通过频率响应的方法得到涡扇发动机状态依赖的传递函数。郑斐华［12］提出了采用伪随机信号基于系统辨识的航空发动机建模方法。

基于上述讨论，本文借助部件模型、系统辨识等方法，使用混合信号充分刺激部件模型，将某涡扇发动机建模成NPV 系统，该系统能完整地反映涡扇发动机非线性和状态参数在大范围内快速变化的时变特性［13］，更加接近实际对象，为涡扇发动机的控制提供一种新途径。

1 NPV 模型

考虑如下NPV 系统

式中：x∈Rnx、u∈Rnu和y∈Rny分别为系统状态、系 统 输 入 和 输 出，σ(t)∈Rnσ为 时 变 参 数，A(x，σ(t))、B(x，σ(t))、C(x，σ(t))和D(x，σ(t))为关于x和σ(t)的多项式函数。

工程中许多被控对象可采用NPV 系统作为其模型［2⁃3］。特别地，当系统（1）的系统矩阵只依赖时变参数时，退化为线性变参数系统

当系统矩阵仅为关于状态量的多项式时，系统（1）退化成多项式非线性系统

因此，NPV 系统可以看作是多项式非线性系统和LPV 系统的推广。

值得注意的是，文献［1］将涡扇发动机模型建成如式（2）所示的LPV 系统，其系统矩阵是关于高压转子转速绝对量的多项式，而状态则是其增量形式，形如

该建模方式只是原系统在工作点的一阶近似，系统参数依旧只是调度参数，忽略了涡扇发动机系统的强非线性。本文借助部件级模型和系统辨识等方法，使用混合信号充分激励部件级模型，把涡扇发动机系统建模成如下多项式模型

继而建立了涡扇发动机全包线的NPV 模型，系统矩阵是发动机状态和时变参数的多项式，显式地体现涡扇发动机的非线性和时变特性，弥补LPV 系统建模的不足。

2 涡扇发动机大包线建模方法

以某型小涵道比双轴涡扇发动机为研究对象，其非线性数学模型可以描述为［14］

式中：x∈Rnx、u∈Rnu和y∈Rny分别为系统状态、系统输入和输出。

2.1 单个稳态点状态变量模型

设(xe，ue，ye)为 涡 扇 发 动 机 系 统 的 一 个 稳 态点，该稳态点附近系统（6）可化为

式中：Ae、Be、Ce、De为待定系统矩阵。

本 文 选 择x=[nLnH]T，u=[Wfb A8]T，y=[nHπ]T，其中，nL为低压转子转速，nH为高压转子转速，Wfb为主燃油量，A8为喉道面积，π为发动机的增压比。

设采样周期为T，kT时刻的状态、输入和输出分别记为x(k)、u(k)和y(k)，采用欧拉积分的方法离散化如下

假设发动机非线性模型在稳态点(xe，ye)附近受扰动信号 Δu生成了输入输出数据：{(x(k)，y(k))，k=0，1，…，N}，N为采样个数。

记偏差量数据矩阵为

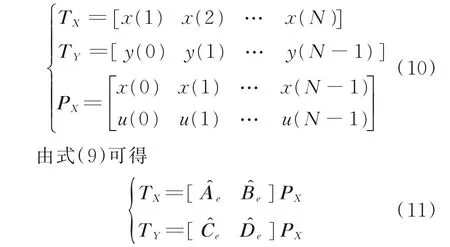
基于最小二乘法，在部件级模型的状态量与状态空间模型的状态量误差平方和最小情况下，则系统矩阵参数的解为

由式（9）可确定在稳态点(xe，ue，ye)模型（7）。

2.2 典型工作点的多项式模型

在某一飞行条件下，即取固定高度H和马赫数Ma，选 取N1个 稳 态 点 (xei，uei，yei)，i=1，2，…，N1。对稳态点(xei，uei，yei)，按2.1 节中方法得到模型参数矩阵为(Aei，Bei，Cei，Dei)。采用多项式拟合方法，建立典型工作点的发动机多项式非线性模型

非线性系统（13）中系统矩阵求解步骤如下：

（1）记

则由实例点构成的集合为

记F是由xei到Aei的函数集合，则

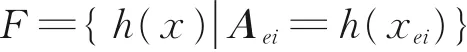
令h(x)=ωx，ω=[ω1…ωN1]T为 多 项式模型的系数向量。

由于涡扇发动机nH更能近似反映发动机的机械载荷和热载荷变化状况［16］，以及直接反映动态特性变化，故式（13）中系统矩阵只为nH的函数。

2.3 大包线NPV 模型

在飞行包线内，选取N2个典型工作点(Mai，Hi)，i=1，2，…，N2。按2.2 节中方法建立第i(i=1，2，…，N2)个典型工作点的多项式模型

在 包 线 0 ≤Ma≤1.2，0 ≤H≤8 内，将(A(x)(Mai，Hi)，B(x)(Mai，Hi)，C(x)(Mai，Hi)，D(x)(Mai，Hi))，i=1，2，…，N2，利 用 回 归 算 法 分 别 拟 合 成 如 下形式

σ(t)=(Ma，H)是关于高度和马赫数的多项式函数，则得到涡扇发动机大包线模型。

3 某型涡扇发动机建模

本部分基于系统辨识的方法在不同飞行条件下获取不同高压转速下的状态空间模型，再通过多项式拟合和回归方法获取各系统矩阵关于时变参数与状态变量的多项式描述。为了消除数据特征之间的量纲影响，将调度参数归一化至[0，1]。

3.1 激励信号及辨识算法

根据流量连续和功率平衡的共同工作方程建立的部件级模型，对其信号激励得到输入输出数据。采用阶跃信号冲击部件级模型得到的输入输出数据无法刻画涡扇发动机的动态特性，且一步求解最小二乘问题时拟合程度不高。若要达到较好的辨识效果，则需多步系统辨识，计算量较大且动态过程一般。因此，有学者采用伪随机序列［17］（Pseudo random binary sequence，PRBS）冲击部件级模型，PRBS 是由周期性数字序列经过滤波处理得到，具有可重复性、自相关性能好的特点，如图1所示。经过仿真验证，相比使用阶跃信号，采用PRBS 能够充分激励部件级模型，得到更好的结果，但其结果模型泛化性能很差。

图1 伪随机序列Fig.1 Pseudo random binary sequence

本文结合机器学习中训练集的思想，提出一种基于阶跃信号、正弦信号以及伪随机信号的混合信号。采用上下界幅度在稳态燃油幅度的±2%左右的混合信号，即一定幅度的M 序列，阶跃信号以及一定幅值和频率的正弦信号，如图2所示。相比使用单一信号，采用混合信号可以充分激励部件模型，得到更好的结果，且结果模型泛化性能较好。

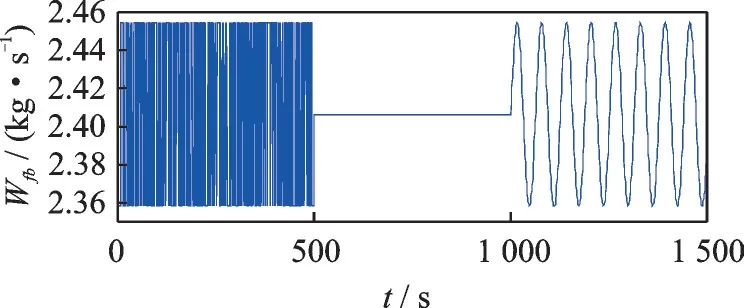
图2 混合信号Fig.2 Mixed signal

辨识采用的最小二乘算法为Levenberg⁃Mar⁃quardt（L⁃M）估计算法［18］。L⁃M 算法的每一步迭代都可以调整阻尼项以确保误差下降。当远离最优解时，算法接近最速下降法。反之，则接近高斯牛顿（Gauss⁃Newton，G⁃N）算法，利用二阶导数的信息，快速收敛到最优解。

在一定飞行条件和某工作状态下分别使用阶跃信号、伪随机信号和混合信号激励部件级模型，利用L⁃M 算法对部件模型的输入输出数据进行动态辨识，验证激励信号对于系统辨识的影响。本文以地面条件为例，nH的误差大小作为评价辨识效果的好坏，结果分别见表1 和图3～7，其中，图3、5、7 中两条曲线分别代表部件级模型的输出转速和辨识结果的输出转速曲线。图4 为伪随机信号激励下辨识模型与部件级模型阶跃响应曲线。图6为混合信号激励下辨识模型与部件级模型阶跃响应误差曲线。

图3 伪随机信号激励下的系统辨识结果Fig.3 System identification results under pseudo random signal excitation

图4 伪随机信号辨识结果的验证Fig.4 Validation of identification results of pseudo random signal systems

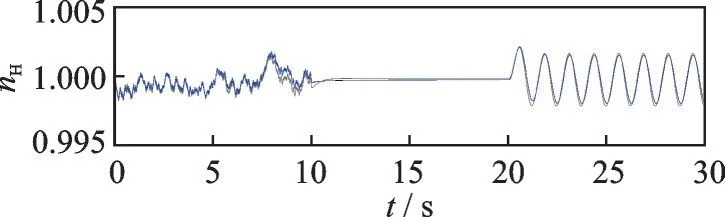
图5 混合信号激励下的系统辨识结果Fig.5 Identification results with mixed signal excitation

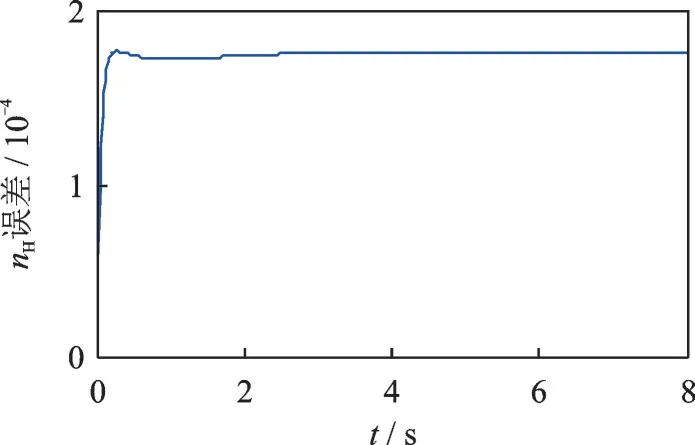
图6 混合信号激励下的系统辨识误差Fig.6 System identification error with mixed signal excita⁃tion

表1 激励信号的辨识误差及验证误差Table 1 Identification error and validation error of exci⁃tation signal %

图7 G-N 算法下的系统辨识结果Fig.7 System identification results under G-N algorithm

由图3、4 可知，伪随机信号输入有很好的动态辨识效果，但在验证的过程中，该状态空间模型的泛化性能很差，出现发散现象。

由图5、6 可知，采用混合信号输入的辨识结果较好。混合信号提高了最小二乘的拟合程度，且结果模型具有较好的泛化能力，在验证过程中误差不超过0.02%。

由图5、7 可知，求解涡扇发动机系统辨识最小二乘问题，采用L⁃M 估计方法的平均误差为0.01%，采用G⁃N 算法得到的最优值的平均误差为0.55%。因此，采用L⁃M 估计方法求解的精度更高。

3.2 典型工作点的多项式模型验证

通过混合信号与L⁃M 算法系统辨识得到地面条件下20 个工作状态的线性系统，通过多项式拟合建立地面条件下的多项式非线性系统为

非线性系统（15）的矩阵参数拟合结果如图8～11 所示（篇幅有限，仅列出A(x)拟合结果）。

图8 系数a11 拟合曲线Fig.8 Fitting curve of a11

为了检验多项式非线性系统的精度，将其与非线性动态热力学模型［19］分别做较大范围仿真验证，仿真结果如图12、13 所示。

由图12、13 可知，本文建立的多项式非线性系统能够较精确地反映原系统动态特性，且稳态误差在0.5%以内。由于篇幅有限，未列出其他飞行条件下的多项式非线性模型。

图9 系数a12 拟合曲线Fig.9 Fitting curve of a12

图10 系数a21 拟合曲线Fig.10 Fitting curve of a21

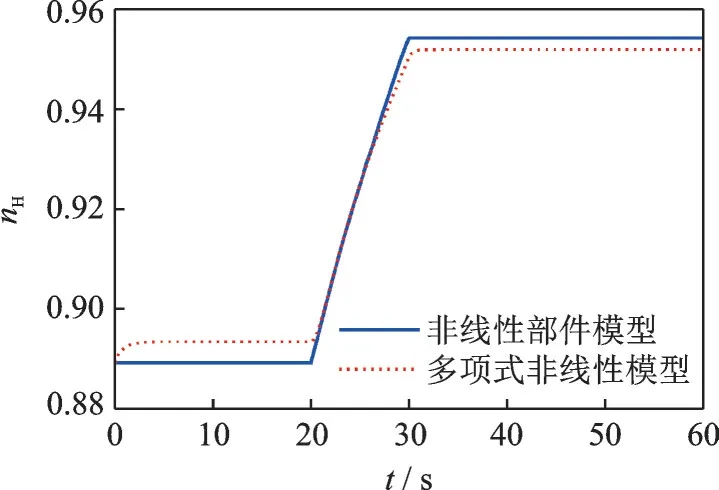
图12 nH=0.89 至nH=0.95 仿真验证Fig.12 Simulation verification from nH=0.89 to nH=0.95

图13 nH=0.95 至nH=0.99 仿真验证Fig.13 Simulation verification from nH=0.95 to nH=0.99

3.3 大包线NPV 模型验证

本部分将各飞行条件（表2）的模型通过回归算法得到大包线NPV 模型如式（16）所示。

表2 大包线H 和MaTable 2 Large envelope H and Ma

式中aij，bij，cij和d2j（i，j=1，2）分别为

为了检验NPV 模型的精度，将NPV 系统与非线性动态热力学模型做仿真验证，仿真结果如图14～17 所示。

由图14～17 可知，NPV 系统与非线性动态热力学模型误差较小，不超过1%。

图14 Ma=0.3,H =3 时nH=0.91～1.04 仿真验证Fig.14 Simulation verification of nH=0.91—1.04 with Ma=0.3,H =3

图15 Ma=1.2,H =8 时nH=1.0～1.044 仿真验证Fig.15 Simulation verification of nH=1.0—1.044 with Ma=1.2,H =8

图16 Ma=0.7,H =6 时nH=0.973～1.039 仿真验证Fig.16 Simulation verification of nH=0.973—1.039 with Ma=0.7,H =6

图17 Ma=0.2,H =2 时nH=0.881～0.946 仿真验证Fig.17 Simulation verification of nH=0.881—0.946 with Ma=0.2,H =2

4 结 论

本文将一种混合信号作为激励信号，采用L⁃M 算法求解最小二乘问题，采用系统辨识方法，建立了涡扇发动机NPV 模型。NPV 系统矩阵参数能够根据高度、马赫数以及高压转子转速实时改变，能更好地刻画涡扇发动机的强非线性、时变特性以及大转速范围的动态特性，为涡扇发动机的控制设计提供了一种新途径，是进一步研究涡扇发动机稳态及过渡态控制的基础。在该NPV 建模方法的基础上，下一步将开展增量形式NPV 模型建模研究。