基于机器学习和全极化雷达数据的干旱区土壤湿度反演

杨丽萍，侯成磊，苏志强，白宇兴，王 彤，冯 瑞

基于机器学习和全极化雷达数据的干旱区土壤湿度反演

杨丽萍1，侯成磊2,3，苏志强2，白宇兴2，王 彤1，冯 瑞2

（1. 长安大学地质工程与测绘学院，西安 710054；2. 长安大学地球科学与资源学院，西安 710054；3. 山东农业工程学院国土资源与测绘工程学院，济南 250100）

雷达遥感是区域土壤湿度监测最为有效的技术手段之一，为深入探讨全极化雷达特征参数和不同机器学习算法对干旱区土壤湿度反演的潜力，该研究以黑河下游的居延泽为研究区，基于全极化Radarsat-2数据，通过标准强度和相位处理提取后向散射系数（Backscattering Coefficients，BC），并通过Cloude-Pottier分解（Cloude-Pottier Decomposition，CPD）与Yamaguchi分解（Yamaguchi Decomposition，YD）提取多个极化参数作为雷达影响因子，对其进行相关性及重要性分析。采用随机森林（Random Forest，RF）、支持向量机（Support Vector Machine，SVM）和BP人工神经网络（Back Propagation Artificial Neural Network，BP-ANN）3种不同的机器学习算法，构建土壤湿度反演的多种模型，并使用10折交叉验证的方法综合评价各模型的性能，最后使用最佳模型反演研究区土壤湿度，分析其空间分布格局与影响因素。结果表明：1）平均散射角对反演精度至关重要，熵与反熵的影响次之。交叉极化相较于同极化后向散射系数有更高贡献，偶次散射与体散射的重要性明显高于表面散射和螺旋体散射。2）不同类型因子组合建模的模型，其性能表现均明显优于仅采用单种因子类型的模型。3）相较于SVM和BP-ANN模型，RF模型在干旱区土壤湿度反演中具有更好的适用性。其中，BC+CPD组合训练的RF模型性能最优，其验证集决定系数2和均方根误差分别为0.78和6.60%，对应的标准偏差分别为0.15和1.95%，该模型可解释土壤湿度变化的89%。4）研究区土壤湿度平均值约为8.83%，整体呈现极端干旱的态势。其中，天鹅湖附近和古湖心区的土壤湿度高于其他区域，反演结果能综合反映区域土壤湿度空间分布的总体格局。

土壤湿度；模型；算法；RF；SVM；BP-ANN；Radarsat-2；干旱区

0 引 言

土壤湿度是控制陆地-大气界面的水分、能量和碳交换等生物物理过程的基本状态变量，是水文学、气象学、生态学和农业环境研究的重要参数[1]。中国西北干旱区降水稀少，水资源极其匮乏，生态环境问题突出，土壤湿度在干旱区水循环和能量平衡中扮演着十分重要的角色，对干旱区生态系统演变具有明显的控制作用[2]。干旱区土壤湿度的准确监测对于区域陆地表面过程的科学研究及生态环境的可持续发展具有重要意义[3]。

土壤湿度时空异质性特征明显，传统的监测方法无法及时、连续、准确地获取大面积的土壤湿度信息。雷达遥感由于具有全天候、全天时以及对土壤湿度高度敏感的特点，已成为区域尺度土壤湿度监测的重要技术手段。其中，全极化合成孔径雷达（Fully Polarimetric Synthetic Aperture Radar，PolSAR）技术不仅能够获取目标地物的后向散射信息和几何结构信息，更为重要的是，它能够同时获取目标地物的极化信息，为土壤湿度和地表粗糙度等相关参数的精确反演提供了可靠的信息来源。因此，关于极化特征参数与土壤湿度之间相互关系的探讨备受国内外学者关注，简单线性统计回归的方法是最为常用的方法之一。Bourgeau-Chavez等[4]基于干湿季时间序列全极化Radarsat-2数据反演了美国阿拉斯加北方黑云杉林地区的土壤湿度，认为极化特征参数在一定程度上能够提高土壤湿度的反演精度。Xie等[5]基于多种极化参数反演了不同时期玉米地的土壤湿度，取得了较好效果，认为PolSAR数据在土壤湿度反演中具有较大应用潜力。然而，土壤湿度与极化特征参数之间关系复杂，线性统计回归模型虽然可以从一定程度模拟这一关系，但由于模型相对简单，适用范围有限，模拟精度有待进一步提升，二者之间非线性关系模型的研究亟待深入。因此，建立多种极化特征参数与土壤湿度之间更为有效和精确的遥感反演模型，是充分挖掘PolSAR影像中所蕴含的极化信息，促进区域土壤湿度雷达遥感反演走向实用化的关键问题，机器学习技术为解决这一问题提供了可能。

大量研究表明，在多参数、多类型、非线性、复杂映射关系的定量模拟中，相对于传统的统计回归模型而言，以随机森林（Random Forest，RF）、支持向量机（Support Vector Machine，SVM）和BP人工神经网络（Back Propagation Artificial Neural Network，BP-ANN）等为代表的机器学习模型性能更为优越[6-7]，在土壤湿度遥感定量反演中已得到广泛应用[8-13]。为克服被动微波地表土壤湿度产品空间分辨率较低的不足，Zhao等[7]在伊比利亚半岛基于RF模型研究了土壤湿度主被动探测卫星（Soil Moisture Active and Passive，SMAP）土壤湿度产品的空间降尺度方法。研究发现，基于RF模型的降尺度方法能够较好地反映土壤湿度的变化，有利于提高被动微波土壤湿度产品的分辨率并促进其在小尺度范围的应用。曾旭婧等[8]基于小兴安岭西北的北安-黑河高速公路沿线地区的Sentinel-1 A影像，利用SVM模型，针对草地、牧场和冬小麦等不同植被覆盖地表，对比了单极化、双极化等不同极化组合方案的土壤湿度估算效果。认为单极化中，VV极化优于VH极化，双极化去极化比率适用于低植被区，VV极化与归一化植被指数组合可综合反映复杂地表环境下的土壤湿度。王雅婷等[9]协同利用全极化Radarsat-2和高分1号数据，以内蒙乌审旗毛乌素沙漠腹地的风沙滩地区为研究区，采用水云模型剔除稀疏植被对湿度反演的干扰，开展了干旱区稀疏植被覆盖条件下土壤湿度的SVM遥感建模研究。针对组合粗糙度的不同情况，探讨了不同极化方式下后向散射系数对反演精度的影响。研究发现，仅采用后向散射系数的单数据源模型中，同极化后向散射系数模型精度更高。加入组合粗糙度参数的多数据源模型，各极化方式的模型精度均有所提升，而VV极化表现最佳。Alexakis等[10]结合多时相Sentinel-1和Landsat-8影像，基于后向散射系数、归一化植被指数、热红外温度和入射角等参数，构建了希腊克利特岛西部0～5 cm表层土壤湿度反演的BP-ANN模型，该模型反演精度高，对流域水文模拟研究意义重大。前人研究表明，RF模型能够减少偏差并防止过拟合，SVM模型外推能力突出，而BP-ANN模型具备良好的网络柔性。由于各具特色，因此，很多学者就土壤湿度反演中不同机器学习模型及其与传统模型的反演效果进行了对比。李平湘等[11]针对冬小麦返青、拔节和乳熟3个物候期，基于全极化Radarsat-2影像的多种后向散射系数和极化特征参数，构建了河北省保定市定兴县不同植被覆盖下土壤湿度反演的RF模型，与SVM和ANN模型的对比表明，RF模型性能更佳。王浩等[12]基于谷歌地球引擎（Google Earth Engine，GEE）平台中的Sentinel-1 SAR数据、MODIS地表生物物理参量产品和SRTM DEM数据，以中亚锡尔河流域中下游4个农田子区域为研究区，对比分析了上述3种机器学习模型在干旱区土壤湿度反演中的效果及适用性，认为基于与土壤湿度显著相关的27个因子所构建的RF模型具有最高反演精度。郭交等[13]基于陕西杨凌示范区冬小麦生长初期的Sentinel-1和Sentinel-2影像，对比了Oh模型以及SVM和ANN模型对农田地表土壤湿度估算的效果，认为水云模型的加入可消除植被影响，提高Oh模型的精度，但考虑植被指数的2种机器学习模型精度更高，在综合考虑后向散射系数、植被指数、海拔和局部入射角的情况下，SVM模型表现最佳，其测试集的2和均方根误差分别为0.903和0.015%。

综上可见，协同利用机器学习和PolSAR数据的土壤湿度遥感反演研究发展迅速，然而，干旱区类似工作有限，亟需开展相关研究及广泛验证。本文以中国干旱区的典型代表居延泽为研究区，基于全极化Radarsat-2数据提取土壤湿度雷达影响因子，结合实测数据，探讨RF、SVM和BP-ANN模型在干旱区土壤湿度遥感反演中的效果和适用性。研究成果有望促进土壤湿度遥感建模研究及区域旱情监测和生态环境的可持续发展。

1 研究区概况

居延泽位于内蒙古西部，是中国第二大内陆河黑河的尾闾湖之一，地理坐标介于41°45′N～42°10′N、101°31′E～102°00′E之间（图1），东居延泽、西居延泽共同构成居延泽古湖盆。湖盆东为茫茫戈壁，南抵巴丹吉林沙漠，西接额济纳绿洲，北隔阿尔泰山脉与蒙古国接壤，天鹅湖位于湖盆西北角。全区多年平均降雨量不足40 mm，多年平均蒸发量为降雨量的100倍之多。由于身居内陆，气候极端干旱，植被稀少，荒漠、戈壁和盐碱地广布，自然条件极端恶劣，水资源是影响区域可持续发展的关键限制因子。

2 数据来源与研究方法

2.1 数据来源

2.1.1 实测数据

受区域极其严酷的环境条件所限，在考虑可通达性的情况下，卫星过境期间，共采集50个土壤采样点（图1）。其中，西居延泽南部20个样点、东居延泽北部6个样点、西居延泽南北向13个样点、天鹅湖附近11个样点，样点设计涵盖区域所有地物类型。通过人工开挖探坑的方法分层采集土壤样品，探坑长、宽、深均约为50 cm。本文利用表层0～10cm的土壤样品，通过烘干法[14]测量得到土壤体积含水率以表征土壤湿度，其范围为0.23%～38.07%。

2.1.2 遥感数据

采用居延泽地区2017年8月17日C波段Radarsat-2精细全极化模式影像，幅宽为25 km×25 km，分辨率为8 m，入射角为32.13°，影像处理级别为单视复数图像（Single Look Complex，SLC）。利用ENVI SARScape插件进行多视和几何校正等预处理后，为减少斑点噪声，选择5×5像素窗口，利用PolSARpro软件进行Lee滤波处理。随后，经矩阵变换，将图像转换为对称协方差矩阵。最后，提取各采样点的后向散射系数和极化特征参数，各样点值以5×5像素窗口内像元值的平均值表示。

2.2 研究方法

首先，根据标准强度和相位处理、Cloude-Pottier分解（Cloude-Pottier Decomposition，CPD）[15]和Yamaguchi分解（Yamaguchi Decomposition，YD）[16]对Radarsat-2影像进行处理，获取雷达图像的后向散射系数与多个极化参数作为雷达影响因子；其次，讨论各因子与实测土壤湿度之间的相关性，并对雷达影响因子进行重要性评分；第三，对BC、CPD和YD相关因子进行组合，形成单种类型和不同类型因子组合的多种方案，作为输入因子，构建多种方案下的机器学习模型；第四，采用k折交叉验证的方法，基于决定系数2、均方根误差（Root Mean Square Error，RMSE），以及二者相应的标准偏差（Standard Deviation，SD），即SDR2与SDRMSE，从精确性、准确性与稳定性3个方面，定量评价各模型的综合性能；最后，基于最佳模型开展区域土壤湿度的遥感反演，并就其空间分布格局与主要影响因素进行探讨。本文技术流程如图2所示。

2.2.1 雷达影响因子提取

利用标准强度和相位处理、CPD和YD这2种极化分解方法，对Radarsat-2影像进行处理，提取相关参数，作为机器学习模型输入因子。

1）标准强度和相位处理

PolSAR可以发射并接收水平（H）或垂直（V）极化的电磁波，并利用一个复二维矩阵，即极化散射矩阵完整地记录电磁波与地物作用时，在4种不同极化状态下的信息。该矩阵表达式如下[17]：

式中下标HH、HV、VH和VV表示4种不同的极化方式，散射单元HH代表水平发射和水平接收，VH代表垂直发射与水平接收，HV和VV定义类似。由于散射矩阵单元以复散射振幅表示，且其具有强度差异和相位延迟[18]，因此，通过标准强度和相位处理，提取4种极化方式下的后向散射系数，即σ、σ、σ和σ。

注：RF为随机森林，SVM为支持向量机，BP-ANN为BP人工神经网络。下同。

Note: RF is random forest, SVM is support vector machine,BP-ANNis back propagation artificial neural network. Same as below.

图2 技术流程图

Fig.2 Technology flowchart

2）极化目标分解

极化目标分解是为了充分利用雷达极化信息而发展起来的一种全极化SAR数据处理技术。通过对散射矩阵或协方差和相干矩阵的分解，将具有复杂散射方式的目标地物表示为简单目标的矩阵之和，以获取更为详尽的地物几何形态与物理参数信息[19]。极化目标分解包括针对纯目标的相干分解和针对分布式目标的非相干分解两大类，非相干分解以协方差或相干矩阵为基础，更适用于随机特性明显、极化特征多变的自然地表，其中，CPD和YD是常用的非相干分解技术。

① Cloude-Pottier分解

19世纪90年代，Cloude和Pottier提出了一种基于特征向量/特征值的极化分解方案CPD，其将相干矩阵分解为3个正交酉矩阵的加权和，表达式如下[15]：

式中λ代表特征值，为非负实数；V代表特征向量，*代表复共轭转置。

基于CPD得到特征值和特征向量，然后得到以下参数[15,20-22]：

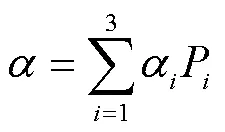
式中′代表熵；代表平均散射角，(°)；代表反熵；RVI代表雷达植被指数；α代表特征向量所表示的散射机制，λ代表目标相干矩阵的3个特征值，P为由特征值λ得到的概率。

② Yamaguchi分解

YD是在Freeman分解基础上发展的一种四元极化非相干分解模型，除考虑表面散射f、偶次散射f和体散射f之外，还考虑了螺旋体散射f，模型框架如下[16-17]：

式中f、f、f和f代表4种散射分量系数，odd、dbl、vol和hlx代表相应的协方差矩阵。

2.2.2相关性与重要性分析

为了理解不同影响因子对模型反演结果的贡献并分析不同组合方案下机器学习模型性能表现的差异，需要计算各影响因子与土壤湿度的相关性及其重要性分数。重要性分数由平均精度减少（Mean Decrease Accuracy，MDA）表示，其表示当该因子被随机置换时精度的平均减少量。

2.3 机器学习模型及调参策略

2.3.1 随机森林

RF模型由一系列二叉分类决策树所构成，为获得较高的预测精度，模型利用训练数据集随机生成大量单一的决策树形成森林，将各棵决策树回归预测的结果进行聚合，以其平均值作为模型的最终结果进行输出[23]。RF模型可用式（8）表示[24]：

式中代表预测因子，φ代表随机因子序列，代表决策树中的森林总数。本文RF模型的优化基于循环迭代的参数优选策略，通过调整决策树的数量和决策树允许使用特征的最大数量实现。参考前人经验[25]，对于决策树数量，本文以10棵树为步长，将初始数量值设置为10棵，依次递增至300棵，在每一折交叉验证结果中存入2最大的模型。对决策树允许使用特征的最大数量，通过在以上循环下嵌套新循环的方式不断尝试，从而确定当次所对应决策树数量的最佳模型。

2.3.2 支持向量机

SVM是一种以结构风险最小化理论为基础的有监非参数统计学习技术，基于泛化误差上限最小化的原则构建函数[26]。为有效解决非线性分类问题，通过核函数将低维空间向量集映射到高维空间，实现研究样本非线性关系到线性可分的转换，其基本模型如下[24,27]：

2.3.3 BP人工神经网络

BP-ANN模型是基于大量神经元的交互作用，对输入信息进行运算处理，并建立输入和输出因子之间相互关系的一种机器学习模型[29]，由输入层、隐含层和输出层组成。本文通过更改隐含层和每层神经元的数量实现激活函数和网络结构的调整，进而实现模型非线性拟合能力的优化。该模型可表示为[24,30]：

式中x和у分别代表输入和输出因子，w、b和分别代表权重因子、偏差项和激活函数。本文采用单个隐含层的神经网络结构和双曲正切S形激活函数，对输入变量与输出变量进行标准化之后，将其输入BP-ANN模型进行训练。经过大量重复试验，模型中最大训练次数、训练要求精度以及学习率等关键参数分别设置为1 000、0.001和0.01。

2.4 模型验证方法

采用k折交叉验证进行模型验证与性能评估。Kohavi等[31]研究表明，k折交叉验证中，对估计模型预测误差而言，采用10倍的变异系数具有最佳效果。故本文在确保模型外推能力良好的情况下，为避免一定程度的过拟合，采取十折交叉验证的方法，基于以下4个评定指标，从精确性、准确性以及稳定性3个方面对模型性能进行评估。主要指标包括训练集和验证集的决定系数2、均方根误差（Root Mean Square Error，RMSE），以及二者相应的标准偏差SDR2与SDRMSE。通常情况下，2越高，RMSE越低，且SD越接近于0，建模效果越好。

3 结果与分析

3.1 雷达影响因子及其相关性分析

通过标准强度和相位处理、CPD以及YD处理，共得到12个雷达影响因子，包括4种极化方式的后向散射系数、4个CPD产物和4个YD产物（图3）。

表1为土壤湿度（）和各影响因子之间的相关系数矩阵。由表可见，相对于其他因子，、′和这3个因子与土壤湿度之间具有较高的相关性，其中的相关性最高，为0.68，′和与湿度的相关性均在0.50以上，这些因子均为CPD产物，说明CPD产物在土壤湿度反演中潜力巨大；后向散射系数与土壤湿度的相关性与极化方式有关，交叉极化的相关性高于同极化。交叉极化中，σ与土壤湿度的相关系数最高，同极化中，σ与土壤湿度的相关系数最低；YD获取的4个分量中，f与土壤湿度间具有较高的相关性，f与土壤湿度的相关系数最低，为−0.06，且f和f与土壤湿度呈现负相关关系。进一步研究发现，上述因子之间也存在一定的相关性。CPD产物中的和之间以及RVI和之间，同极化后向散射系数σ和σ之间以及交叉极化的σ和σ之间，均存在强烈的正相关关系，而YD产物f与CPD产物之间则存在较高的负相关性。

表1 土壤湿度与12个因子的相关系数矩阵

3.2 影响因子重要性分析

为了理解不同影响因子对模型反演结果的贡献，计算了各因子的MDA，结果如图4所示。由图可见，作为CPD产物，、′与对反演结果有突出贡献，而RVI的重要性相对较低。4种后向散射系数中，交叉极化的σ与σ的重要性明显高于同极化的σ与σ。在f、f、f和f中，f偶次散射的重要性明显高于其余三者。综上可见，相对于后向散射系数与YD产物，CPD产物拥有更高的重要性评分。

3.3 模型反演

基于研究区50个样本获取的σ、σ、σ、σRVI、f、f、f和f与对应样本点的土壤湿度实测值，构建了单种类型因子和不同类型因子组合方案土壤湿度反演的RF、SVM和BP-ANN模型共21个，每类模型7个，模型性能的对比结果如表2所示。

由表2可见，针对所有构建模型，从2来看，训练集的最大值为0.95，最小值为0.31，平均值为0.71；验证集的最大值为0.79，最小值为0.15，平均值为0.50；训练集2总体高于验证集2。从RMSE来看，训练集的最大值为9.17%，最小值为2.36%，平均值为5.64%；验证集的最大值为10.65%，最小值为6.20%，平均值为8.47%；训练集RMSE总体低于验证集RMSE。综上可见，21个模型在训练集取得了优于验证集的综合表现。

针对RF、SVM以及BP-ANN机器学习模型，由表2可见，RF模型的2在训练集与验证集中均高于其他两大类模型，同时，RF模型的大多数RMSE在3大类模型中也是最低，说明与SVM和BP-ANN模型相比，RF模型在土壤湿度估算中效果更佳，具有良好的适用性。

针对不同的因子组合方案，对于单一类型因子组合的各反演模型，如仅基于BC、CPD或YD产物的模型，RF模型验证集的平均2和平均RMSE分别为0.65和8.16%，SVM模型验证集的平均2和平均RMSE分别为0.32和8.62%，而BP-ANN模型的平均2为0.38，其平均RMSE达到10.13%。对于不同类型因子组合建模的各机器学习模型，RF模型验证集平均2为0.76，平均RMSE为6.75%；SVM模型验证集平均2和RMSE分别为0.39和8.63%，BP-ANN模型则分别为0.48和8.91%。综上，相较于使用单一类型因子的模型，不同类型因子组合的各类模型中，RF模型2提高了16.92%，RMSE降低了17.28%，SVM模型2提高了21.88%，RMSE上升了0.12%，BP-ANN模型2提高了26.32%，RMSE降低了11.22%。综合考虑2与RMSE，随着建模因子的增多，模型的2与RMSE分别表现出逐步提高与降低的总体趋势，与单一类型因子构建的模型相比，不同类型因子组合构建的模型性能更佳，其2更高，RMSE更低。由此说明，通过采用不同类型因子的组合方案，可以较为有效地提高土壤湿度的反演精度。

表2 基于10折交叉验证法评估不同模型性能

注：SDR2为决定系数2的标准偏差；SDRMSE为均方根误差（RMSE）的标准偏差。

Note: SDR2indicates the standard deviation of determination coefficient2; SDRMSEindicates the standard deviation of Root Mean Square Error (RMSE).

.

从训练集来看，大部分模型在训练集具有较为优秀的表现，除仅有后向散射系数参与的建模方式外，其余因子组合方案的RF模型训练集2均较高，在0.87到0.90间；结合验证集看，BC+CPD组合训练的RF模型性能表现更加突出，其验证集2和RMSE分别为0.78和6.60%，验证集SDR2与SDRMSE分别为0.15和1.95%，该模型可解释土壤湿度变化的89%。该模型输入的影响因子包括σ、σ、σ和σ这4种后向散射系数，以及和RVI这4种CPD产物。后向散射系数是目前最为常用的土壤湿度反演模型的输入因子，已得到前人的广泛认可和应用[13,32]。CPD产物中，表征全局散射的随机行为，表示次要机制的相对重要性，表征地表由表面散射到二面角散射的变化过程，当其值较低时，将显示更多土壤贡献的成分。本文研究区植被稀少，散射主要源于土壤的贡献。经相关性与重要性分析同样发现，CPD产物对于土壤湿度反演有突出的表现。由于在土壤湿度反演模型中后向散射系数的应用广泛性及CPD产物的相对重要性，因此使得BC + CPD组合训练的RF模型具有最佳性能。

3.4 土壤湿度空间分布

将对应影响因子输入BC+CPD组合训练的RF模型，得到居延泽土壤湿度空间分布图（图5）。

由图5可见，居延泽大部分区域土壤湿度均小于10%，与野外同步实测50个样本点的土壤湿度范围基本一致，整体呈现极端干旱的态势。全区平均土壤湿度仅8.83%，与实测湿度平均值（9.57%）较为接近。西北角的天鹅湖附近、南部以古湖岸堤为界分隔形成的东、西居延泽2个子盆地中心区域，土壤湿度相对较高，其余地区湿度普遍偏低。天鹅湖周围滩涂面积较广，旱芦苇等植被集中生长，具有一定的蓄水能力，因而土壤湿度较高。在西居延泽野外采样过程中发现，古湖区内以盐碱地、沙地为主，生长稀疏、低矮的旱芦苇、白刺和泡泡刺等旱生植被，因而在反演图中可见点状或斑块状分布的湿度高值区。由于地处欧亚大陆腹地，降雨稀少，气候极端干旱，受强烈的蒸发浓缩作用影响，地下水中的盐分随毛管水上升并不断向地表迁移聚集，形成大范围的盐碱地、盐壳和结晶盐壳。气候条件奠定了盐碱地形成的物质基础。在干旱气候条件下，研究区地层中盐分含量高，受物理、化学和生物风化作用，成土母质发生盐化，所释放的盐基离子随水分在地势低洼的古湖盆中心聚集。同时，受多种因素影响，区域内地下水位下降，部分沼泽进一步蜕变为盐碱地，因而具有较高的土壤湿度，东居延泽古湖区表现更为明显。

土壤类型、热量状况以及地表覆盖等因素控制着区域土壤湿度的空间分布格局。研究区内以灰棕漠土、风沙土、盐碱土、潮土和草甸土等土壤类型为主，光照充足，植被稀疏，风蚀强烈，沙地、裸地和盐碱地广布。沙地区域地势平坦，无植被生长，由于质地松散，持水能力差，土壤湿度极低。相对而言，裸地质地较为黏重，利于蓄水保墒，土壤湿度有所提高。植被覆盖区和滩涂区，受植被遮挡，地面温度降低，水分蒸发减少，由于植被对水分的涵养作用以及滩涂区的水源补给，土壤湿度相对较高。此外，湖盆中心区由于干旱少雨，地势低洼，部分盐碱地分布区土壤湿度较高。反演结果与实际相符，能够综合反映区域土壤湿度空间分布的总体格局。

4 结 论

本文利用C波段Radarsat-2全极化雷达数据和实测土壤湿度数据，基于标准强度和相位处理以及2种极化目标分解方法，提取了多个雷达影响因子，评价了不同影响因子的相关性及重要性。基于随机森林（Random Forest，RF）、支持向量机（Support Vector Machine，SVM）和BP人工神经网络（Back Propagation Artificial Neural Network，BP-ANN）3种机器学习算法，构建了土壤湿度反演的多种模型，并对各算法在干旱区土壤湿度遥感反演中的有效性进行了深入探讨，结果表明：

1）平均散射角对反演精度至关重要，熵与反熵的影响次之。4个后向散射系数中，交叉极化的后向散射系数σ和σ比同极化的后向散射系数σ和σ重要性评分更高，与土壤湿度具有更高的相关性。Yamaguchi分解（Yamaguchi Decomposition，YD）的4个产物中，偶次散射f与体散射f拥有更高的重要性。相较于后向散射系数（Backscattering Coefficients，BC）与YD产物，Cloude-Pottier分解（Cloude-Pottier Decomposition，CPD）产物对反演结果贡献显著，重要性评分与相关系数明显高于前两种。

2）对于3种机器学习模型，不同类型因子组合建模的模型性能表现均明显优于仅使用单种因子类型的模型。从验证集的对比看，RF模型2提高了16.92%，RMSE降低了17.28%，SVM模型2提高了21.88%，RMSE上升了0.12%，BP-ANN模型2提高了26.32%，RMSE降低了11.22%。不同类型因子的组合建模可以有效地提高土壤湿度反演模型的性能。

3）综合考虑2与RMSE，相较于SVM和BP-ANN模型，RF模型在干旱区土壤湿度反演中具有更好的适用性，并表现出更为出色的应用潜力。所有模型中，BC+CPD组合训练的RF模型性能最佳，其验证集2和RMSE分别为0.78和6.60%，验证集SD2与SDRMSE分别为0.15和1.95%，该模型可解释土壤湿度变化的89%。

4）研究区土壤湿度平均值仅为8.83%，整体呈现极端干旱的态势。其中，天鹅湖附近和古湖心区相对于其他区域具有较高的土壤湿度。土壤湿度的空间异质性受土壤类型、热量状况以及地表覆盖等多因素综合影响，模型反演结果能综合反映区域土壤湿度空间分布的总体格局。

本文在利用机器学习算法和全极化SAR数据进行干旱区土壤湿度监测方面进行了有益的尝试。值得注意的是，在利用全极化SAR数据进行土壤湿度反演时，无论是传统模型还是基于机器学习的模型中，后向散射系数一直都是广为采用的输入参数。本研究发现交叉极化比同极化后向散射系数拥有更高的重要性评分，这可能是由于不同下垫面的情况下，交叉极化与同极化后向散射系数的重要性存在差异。为了充分挖掘全极化雷达数据中隐含的各种信息，积极开展不同下垫面状况的差异性研究以及全极化雷达成像机理的研究，是今后需要进一步深入的工作。

[1] Santi E, Paloscia S, Pettinato S, et al. Application of artificial neural networks for the soil moisture retrieval from active and passive microwave spaceborne sensors[J]. International Journal of Applied Earth Observation and Geoinformation, 2016, 48: 61-73.

[2] Brocca L, Moramarco T, Melone F, et al. Assimilation of surface- and root-zone ASCAT soil moisture products into rainfall-runoff modeling[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(7): 2542-2555.

[3] Dorigo W, Wagner W, Albergel C, et al. ESA CCI soil moisture for improved earth system understanding: State-of-the art and future directions[J]. Remote Sensing of Environment, 2017, 203: 185-215.

[4] Bourgeau-Chavez L L, Leblon B, Charbonneau F, et al. Evaluation of polarimetric Radarsat-2 SAR data for development of soil moisture retrieval algorithms over a chronosequence of black spruce boreal forests[J]. Remote Sensing of Environment, 2013, 132: 71-85.

[5] Xie Q X, Meng Q Y, Zhang L L, et al. Combining of the H/A/Alpha and Freeman-Durden polarization decomposition methods for soil moisture retrieval from full-polarization Radarsat-2 data[J]. Advances in Meteorology, 2018, 2018: 1-17.

[6] Powell S L, Cohen W B, Healey S P, et al. Quantification of live aboveground forest biomass dynamics with Landsat time-series and field inventory data: A comparison of empirical modeling approaches[J]. Remote Sensing of Environment, 2010, 114(5): 1053-1068.

[7] Zhao W, Sánchez N, Lu H, et al. A spatial downscaling approach for the SMAP passive surface soil moisture product using random forest regression[J]. Journal of Hydrology, 2018, 563: 1009-1024.

[8] 曾旭靖，邢艳秋，单炜，等. 基于Sentinel-1A与Landsat 8数据的北黑高速沿线地表土壤水分遥感反演方法研究[J]. 中国生态农业学报，2017，25(1)：118-126.

Zeng Xujing, Xing Yanqiu, Shan Wei, et al. Soil water content retrieval based on Sentinel-1A and Landsat 8 image for Bei'an-Heihe Expressway[J]. Chinese Journal of Eco-Agriculture, 2017, 25(1): 118-126. (in Chinese with English abstract)

[9] 王雅婷，孔金玲，杨亮彦，等. 基于SVR的旱区稀疏植被覆盖下土壤水分遥感反演[J]. 地球信息科学学报，2019，21(8)：1275-1283.

Wang Yating, Kong Jinling, Yang Liangyan, et al. Remote sensing inversion of soil moisture in vegetation-sparse arid areas based on SVR[J]. Journal of Geo-information Science, 2019, 21(8): 1275-1283. (in Chinese with English abstract)

[10] Alexakis D D, Mexis F K, Vozinaki A K, et al. Soil moisture content estimation based on Sentinel-1 and auxiliary earth observation products. A hydrological approach[J]. Sensors (Basel), 2017, 17(6): 1455.

[11] 李平湘，刘致曲，杨杰，等. 利用随机森林回归进行极化SAR土壤水分反演[J]. 武汉大学学报：信息科学版，2019，44(3)：405-412.

Li Pingxiang, Liu Zhiqu, Yang Jie, et al. Soil moisture retrieval of winter wheat fields based on random forest regression using quad-polarimetric SAR images[J]. Journal of Wuhan University: Information Science Edition, 2019, 44(3): 405-412. (in Chinese with English abstract)

[12] 王浩，罗格平，王伟胜，等. 基于多源遥感数据的锡尔河中下游农田土壤水分反演[J]. 自然资源学报，2019，34(12)：2717-2731.

Wang Hao, Luo Geping, Wang Weisheng. et al. Inversion of soil moisture content in the farmland in middle and lower reaches of Syr Darya River Basin based on multi-source remotely sensed data[J]. Journal of Natural Resources, 2019, 34(12): 2717-2731. (in Chinese with English abstract)

[13] 郭交，刘健，宁纪锋，等. 基于Sentinel多源数据的农田地表土壤水分反演模型构建与验证[J]. 农业工程学报，2019，35(14)：71-78.

Guo Jiao, Liu Jian, Ning Jifeng, et al. Construction and validation of soil moisture retrieval model in farmland based on Sentinel multi-source data[J]. Transactions of the Chinese Society of Agricultural Engineering(Transactions of the CSAE), 2019, 35(14): 71-78. (in Chinese with English abstract)

[14] 张甘霖，龚子同. 土壤调查实验室分析方法[M]. 北京：科学出版社，2012.

[15] Cloude S R, Pottier E. An entropy based classification scheme for land applications of polarimetric SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 1997, 35(1): 68-78.

[16] Yamaguchi Y, Moriyama T, Ishido M, et al. Four-component scattering model for polarimetric SAR image decomposition[J]. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(8): 1699-1706.

[17] Chen S W, Li Y Z, Wang X S, et al. Modeling and interpretation of scattering mechanisms in polarimetric synthetic aperture radar: Advances and perspectives[J]. IEEE Signal Processing Magazine, 2014, 31(4): 79-89.

[18] Zhang B, Perrie W, Vachon P W, et al. Ocean vector winds retrieval from C-band fully polarimetric SAR measurements[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(11): 4252-4261.

[19] 张腊梅，段宝龙，邹斌. 极化SAR图像目标分解方法的研究进展[J]. 电子与信息学报，2016，38(12)：3289-3297.

Zhang Lamei, Duan Baolong, Zou Bin. Research development on target decomposition method of polarimetric SAR image[J]. Journal of Electronics & Information Technology, 2016, 38(12): 3289-3297. (in Chinese with English abstract)

[20] Lee J S, Ainsworth T L, Kelly J P, et al. Evaluation and bias removal of multilook effect on entropy/alpha/anisotropy in polarimetric SAR decomposition[J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(10): 3039-3052.

[21] Cloude S R, Pottier E. A review of target decomposition theorems in radar polarimetry[J]. IEEE Transactions on Geoscience and Remote Sensing, 1996, 34(2): 498-518.

[22] van Zyl J J. An overview of the analysis of multi-frequency polarimetric SAR data[C]//6thEuropean Conference on Synthetic Aperture Radar (EUSAR 2006). Dresden, Germany, 2006: 16-18.

[23] Breiman L, Cutler A. Random forests-classification manual [EB/OL]. [2020-12-25]. https://www.stat.berkeley.edu/～breiman/ RandomForests/ cc_manual.htm.

[24] 雷明. 机器学习-原理、算法与应用[M]. 北京：清华大学出版社，2019.

[25] Min M, Bai C, Guo J P, et al. Estimating summertime precipitation from Himawari-8 and Global Forecast System based on machine learning[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(5): 2557-2570.

[26] Mountrakis G, Im J, Ogole C. Support vector machines in remote sensing: A review[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2011, 66(3): 247-259.

[27] Min M, Li J, Wang F, et al. Retrieval of cloud top properties from advanced geostationary satellite imager measurements based on machine learning algorithms[J]. Remote Sensing of Environment, 2020, 239: 111616.

[28] Chang C C, Lin C J. LIBSVM: A library for support vector machines[EB/OL]. [2021-01-20]. https://ishare.iask.sina.com.cn/ f/11274228.html.

[29] Saha S, Gu F, Luo X, et al. Use of an artificial neural network approach for the prediction of resilient modulus for unbound granular material[J]. Transportation Research Record, 2018, 2672(52): 23-33.

[30] 陈明. MATLAB神经网络原理与实例精解[M]. 北京：清华大学出版社，2013.

[31] Kohavi R. A study of cross-validation and bootstrap for accuracy estimation and model selection[C]//14thInternational Joint Conference on Artificial Intelligence (IJCAI 1995). CA, USA: Morgan Kaufmann Publishers Inc, 1995: 1137-1143.

[32] 蔡庆空，李二俊，陶亮亮，等. PROSAIL模型和水云模型耦合反演农田土壤水分[J]. 农业工程学报，2018，34(20)：117-123.

Cai Qingkong, Li Erjun, Tao Liangliang, et al. Farmland soil moisture retrieval using PROSAIL and water cloud model[J]. Transactions of the Chinese Society of Agricultural Engineering(Transactions of the CSAE), 2018, 34(20): 117-123. (in Chinese with English abstract)

Soil moisture inversion in arid areas by using machine learning and fully polarimetric SAR imagery

Yang Liping1, Hou Chenglei2,3, Su Zhiqiang2, Bai Yuxing2, Wang Tong1, Feng Rui2

(1.,’,710054,; 2.,’710054,; 3.,,250100,)

Soil moisture is one of the most important variablesto affect the water cycle and energy balanceduring theevolution of regional ecosystem in arid areas. However, accurate monitoring of soil moisture is still a challenging task, due to the spatial and temporal heterogeneity. Radar remote sensing has widely been expected to be one of the most effective technologies in regional soil moisture monitoring. Fully polarimetric SAR (PolSAR) can also provide abundant polarized information for different machine learning algorithms to retrieve soil moisture in various regions. However, such research is still lacking in most arid areas, together with the specific evaluation on the performance of different machine learning algorithms. This study aims to retrieve the soil moisture in arid areas using the PolSAR parameters and various machine learning algorithms. The study area was selected as Juyanze region located in the southeast of Ejina banner of Inner Mongolia in western China. Basedon Radarsat-2 imagery, radar variables were set as the extractedbackscattering coefficients (BC) using the standard intensity and phase processing, while the multiple polarimetric parameters that derived from Cloude-Pottier decomposition (CPD) and Yamaguchi decomposition (YD). The parameter correlation and importance were also analyzed after that. Then, 21 soil moisture inversion models were established using three machine learning algorithms, namely Random Forest (RF), Support Vector Machine (SVM), and Back Propagation Artificial Neural Network (BP-ANN). Model performance was further evaluated using 10-fold cross-validation. Finally, the optimal model was achieved to inverse soil moisture in the study area, where the spatial distribution pattern was analyzed. The results show that: 1) The average scattering angle presented the most prominent influence on the inversion accuracy, followed by entropy and anti-entropy among all the variables. Moreover, cross-polarized backscattering coefficients made much more contribution to the model accuracy, compared with the co-polarized backscattering coefficients. The importance of even scattering and volume scattering was remarkably higher than that of surface scattering and spiral scattering. Parameters derived from CPD made outstanding contributions to the retrieval,where the importance scores and correlation coefficients were much higher than those of backscattering coefficients and parameters derived from YD. 2) The developed models of soil moisture inversion under the combined scheme of various variable types performed better than those built solely on single variable type in all three machine learning algorithms, indicating that the combined scheme greatly improved the accuracy of models.3) RF model was more suitable for soil moisture inversion in arid areas,compared with SVM and BP-ANN, according to the determination coefficient2and the root mean square error (RMSE). The model performed best using BC + CPD scheme as input variables. The validation set2and RMSE were 0.78 and 6.60%, respectively, with the standard deviation of2and RMSE of 0.15 and 1.95%, respectively. Consequently, 89% moisture variation can be explained by this optimal model. 4) Generally speaking, soil moisture in the study area maintained at a low level, and the average soil moisture content was 8.83%. Moisture content around the Swan Lake and the center of Paleolake was obviously higher than other areas. The inversion data conformed greatly to the actual situation, indicating a great potential to soil moisture inversion in arid areas.

soil moisture; models; algorithms; RF; SVM; BP-ANN; Radarsat-2; arid areas

杨丽萍，侯成磊，苏志强，等. 基于机器学习和全极化雷达数据的干旱区土壤湿度反演[J]. 农业工程学报，2021，37(13)：74-82. doi：10.11975/j.issn.1002-6819.2021.13.009 http://www.tcsae.org

Yang Liping, Hou Chenglei, Su Zhiqiang, et al. Soil moisture inversion in arid areas by using machine learning and fully polarimetric SAR imagery[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2021, 37(13): 74-82. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2021.13.009 http://www.tcsae.org

2021-01-18

2021-03-16

国家自然科学基金资助项目（41371220、42071345）

杨丽萍，博士，副教授，研究方向为定量遥感及3S应用。Email：zylpyang@chd.edu.cn

10.11975/j.issn.1002-6819.2021.13.009

S152.7; TP79

A

1002-6819(2021)-13-0074-09