异步多速率多传感器网络及在导航制导中的分布式融合估计
2021-09-16李同德严怀成
李同德,严怀成,周 革,范 莎,洪 君
(1.华东理工大学能源化工过程智能制造教育部重点实验室,上海 200237;2.上海机电工程研究所,上海 201109)
0 引言
在过去的几十年中,多传感器网络系统(mutlisensor network system,MSNS)和信息融合引起了广泛的关注,并已被广泛应用于许多领域,例如导航制导、目标跟踪、工业监控、机器人路径规划、运输、财务控制系统等。多传感器信息融合估计是信息融合的重要分支,它使用来自每个传感器的有用信息来估计过程中的参数[1]。与集中式状态融合估计相比,分布式状态融合估计由于具有通信数据压缩、计算需求减少和高容错性等优点而更为可取[2-3]。因此,学者们广泛使用多传感器系统的分布式融合估计算法。在导航制导的实际运用中,文献[4]通过利用卫星、雷达、光电3 种感知传感器的组合导航,借鉴全球导航卫星系统对完好性水平的定义及计算方法,研究了全球导航卫星系统/雷达/光电多传感器组合导航系统完好性的评定方法。
基于多传感器信息融合技术的导航制导成果目前也是十分丰富的。在针对火星定点采样、载人登陆和基地构建等任务的需求研究中,学者们提出了一种火星精确定点着陆多信息融合自主导航与控制方案,而对于多智能体导航系统,则提出了在不同噪声影响下具有更高估计精度的算法[5-6]。多传感器信息融合技术在船舶领域导航信息系统也有很多运用,文献[7]给出了基于信息融合技术的舰船导航信息系统设计方案。当系统处于非线性状态下时,利用扩展卡尔曼滤波器对多源信息进行融合计算,可实现对目标系统的精准定位[8]。
但是,在大多数多传感器导航系统中,由于物理特性及其自身类型的影响,并不能保证每个传感器的采样率都一致。因此,有必要研究多速率多传感器导航系统。文献[9-10]研究了两种异步事件的事件触发机制,这些机制具有不可靠的测量结果和偏差估计,他们都采用扩散估计来处理异步多采样网络系统,可作为异步多速率多传感器融合的未知输入。在文献[11-12]中,对于具有随机非线性的Markov跳跃系统、智能传感器系统和不确定系统,提出了不同的融合估计策略来处理多速率网络系统。文献[13-16]采用了异步采样网络系统的一些基本处理方法,包括插值或增强方法,扩展测量方程的构造等。
在实际的多传感器网络中,由于带宽和能量的限制,每个传感器的测量或本地估计通常不能传输到FC,因此有必要考虑多传感器网络的通信带宽的限制。在文献[17]中,对于具有有限通信带宽的多传感器融合系统,提出了一种新的降维策略和补偿方法。对于遭受重放攻击和拒绝服务(denial of service,DoS)攻击的网络物理系统,当存在带宽限制时,文献[18]和[19]中提出了两种不同的降维方法。对于一类带宽受限的网络化多传感器融合系统,文献[20]和[21]则采用了另一种解决方案,即量化方法。因此,对于异步多速率网络系统,考虑通信带宽的限制并节省传输能量是非常必要的。
本文的主要贡献为:①代替传统的插值或增强方法,采用一种新的增强方法将多速率采样数据系统转换为单速率系统,并采用卡尔曼滤波得到对应的局部估计;②为了满足有限的带宽,设计了降维方法和相应的补偿策略,在获得不同时间的补偿状态估计后,使用SFCI 融合算法获得最终的融合估计;③有限的网络带宽问题所引起的诱导现象被应用到一般的异步MSNS中,从而能更方便地解决一般问题。
1 问题描述
1.1 系统模型和局部最优估计器
考虑一个如下所示的线性离散时间系统:
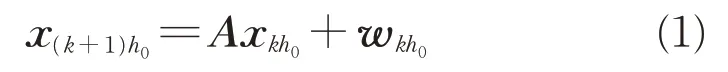
式中:h0是采样周期;和分别是当前状态以及采样瞬间的系统噪声和过程噪声,Rn和Rn×m分别表示n维欧氏空间和n×m实矩阵的集合,k为对应的采样时刻;A是具有适当尺寸的已知矩阵。在本文中,使用N个具有不同采样周期的传感器来测量来自上述系统模型的信息,并描述了第i个传感器的测量模型,可表达为
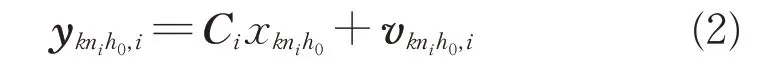
式中:ni是正整数是采样瞬间knih0的测量输出;和分别是测量矩阵和测量噪声。而且,和是不相关的零均值高斯白噪声,满足
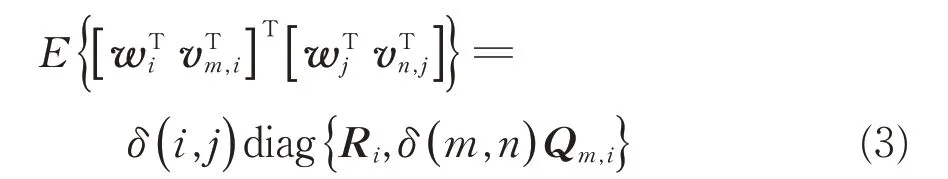
式中:δ(i,j)[or δ(m,n)]是增量函数,例如,如果t≠t1,δi,j=0,否则δi,j=1;Ri和Qm,i分别代表wkh0和vknih0,i的协方差矩阵。初始状态x0是带有和的随机变量,并且满足正态分布假设和彼此独立,同时假设(A,Ci)是可观的,(A,I)是可控的。在文中,为简化表示,采样时刻knih0用kni表示。
对于每个间隔[kni+1,(k+1)ni],式(1)所示的离散时间随机系统可以表示为
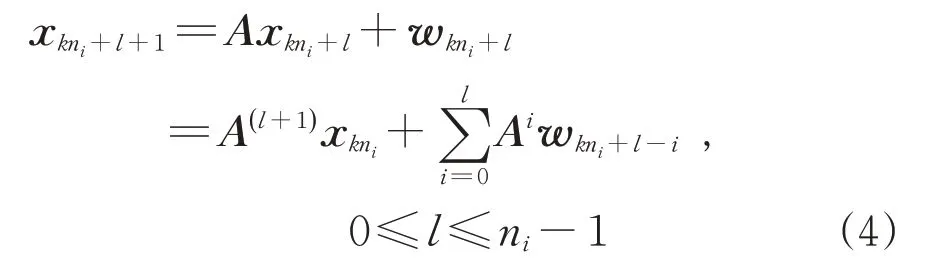
因此,当l=ni-1 时,可以将第i个传感器的测量模型转换为单速率系统,可表达为
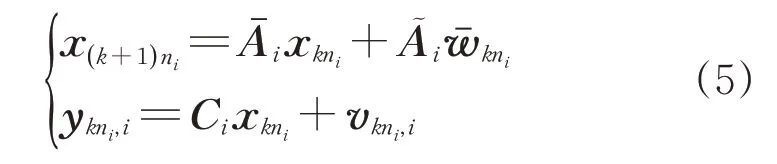
对于i=1,2,⋅⋅⋅,N,有
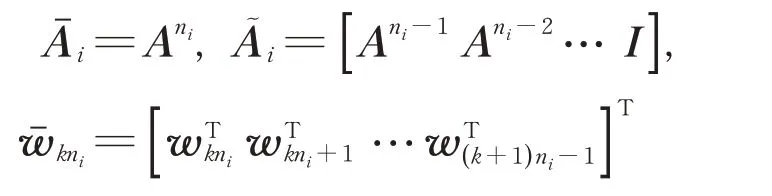
假设使用智能传感器,则每个传感器都可以获取其本地估计值。然后,基于来自第i个传感器的测量ykni,i,通过著名的卡尔曼滤波器递归计算局部最优估计,可表达为
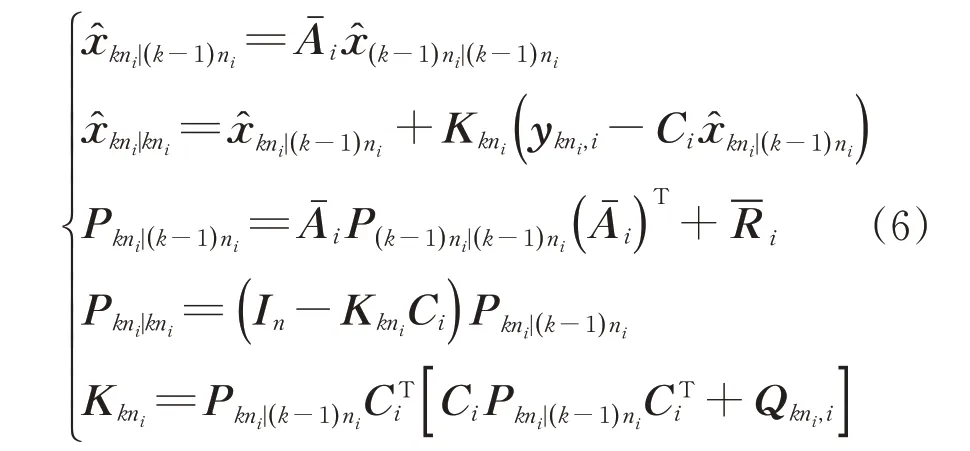
对于i=1,2,⋅⋅⋅,N,有

1.2 通信带宽约束建模
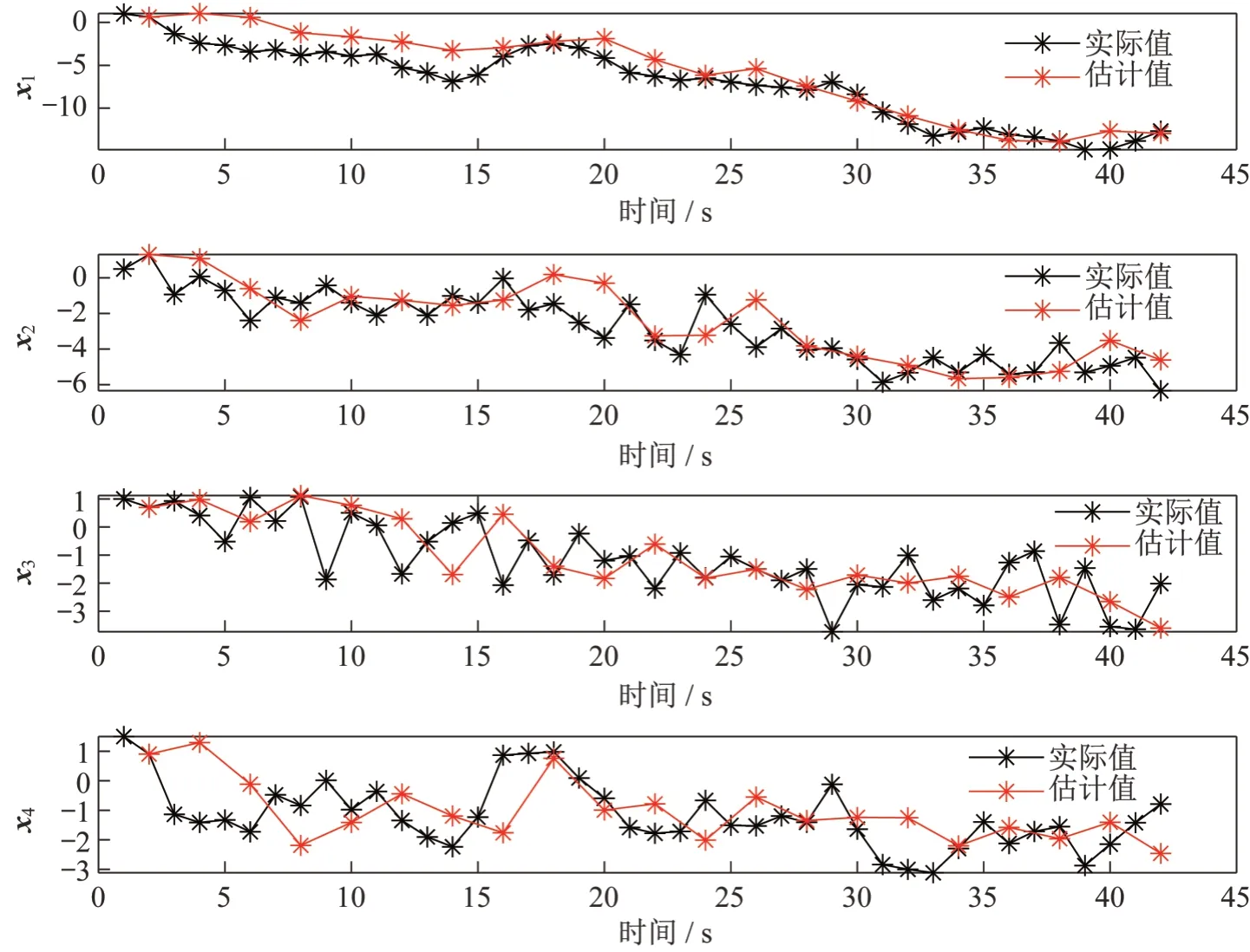
本文采用文献[16]中的降维方法来满足有限的通信带宽。为了满足有限的通信带宽,只有i个传感器的部分分量rkni,i(1≤rkni,i 因此,带宽约束可以用以下模型表示 式中:r表示全局带宽限制;rkni,i代表局部带宽限制。同时,假定r已知。可以调整这个局部约束的参数rkni,i(i=1,2,…,N),使得式(8)所示约束成立。然而,最优参数rkni,i(i=1,2,…,N)的设计应确保在每个时刻的融合估计性能是最优的。 为了使表述更清楚,二值变量σkni,hi(hi=1,2,…,Δkni,i)描述了每个时刻的分量传输过程,因此它们可以被称为决策变量。那么在融合中心重组的状态估计可以被表示为 因此,第i个局部估计的补偿状态估计——,可以被表示为 对于通信带宽受限的多传感器网络系统,需要解决的问题如下: 定理1:定义如下矩阵 在文献[22]中定义了符号“⊙”和“⊗”。可以得到补偿误差协方差矩阵 由于每个传感器的采样率不同,并且可能无法在某些时刻kh0获得交叉协方差矩阵,因此无法使用一般的矩阵加权融合估计。为了方便融合估计的计算,在文献[23]中采用了SFCI 融合算法,避免了计算交叉协方差矩阵,大大减轻了交叉协方差矩阵的计算负担。 由于可能无法在时刻kh0收集状态估计,因此有必要重新定义一个集合 Ξk,令Ξk={i|k=γini,γi∈N+,i=1,2,⋅⋅⋅,N}。当在时刻kh0集合Ξk是空集,局部估计不能被融合。因此,融合估计和融合“协方差”矩阵分别表示为和。采用多速率融合估计方法,可表示为 在定理2中,使用基于FSCI的融合算法给出了融合“协方差”矩阵的轨迹的上限。 定理2:对于带有局部卡尔曼滤波的多速率多传感器系统(式(5)),基于顺序协方差交叉融合算法,(18)和(19)是一致的,即 在本章中,通过一个对导航系统定位追踪的仿真实例来验证所提出的异步分布式融合方法的有效性和可行性。 考虑具有式(5)所示系统参数的线性离散时间系统: 其中,假设有两个传感器的采样率分别为2h0和3h0。wkh0、vkn1h0,1和vkn2h0,2的协方差分别取为Ri=diag{1,0.8,0.8,0.7}、Qm,1=diag{0.3,0.2,0.2} 和Qm,1=diag{0.4,0.2,0.1}。假定初始值的数学期望和协方差分别为和P0|0=0.1I4,r1=r2=2。 仿真结果如图1~4所示,可以看出采样速率越小,估计越准确,但是总体来说都可以得到很好的估计性能。 图1 滤波器1的实际状态xk及其估计Fig.1 The actual state xk of filter 1 and its estimation 图2 滤波器2的实际状态xk及其估计Fig.2 The actual xk of filter 2 and its estimation 图3 真实状态估计以及融合状态估计Fig.3 The actual state estimation and fusion state estimation 图4 滤波器1、滤波器2和融合“协方差”的迹Fig.4 The trace of fusion"covariance",filter 1 and filter 2 本文针对具有通信带宽约束的多传感器导航系统,研究了多速率传感器的分布式融合估计问题。通过一种新的扩充方法,将多速率采样数据系统转换为单速率系统,然后通过卡尔曼滤波获得其局部估计。为了满足有限带宽,设计了降维方法和相应的补偿策略,在获得不同时间的补偿状态估计后,使用SFCI 融合算法获得最终的融合估计。最后,通过一个对导航系统定位追踪的仿真实例验证了所提出的分布式融合估计方法的有效性。


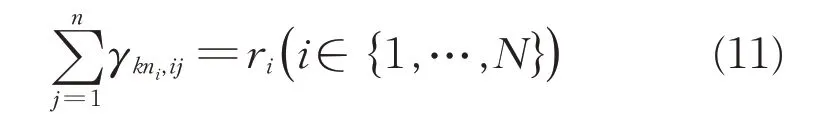
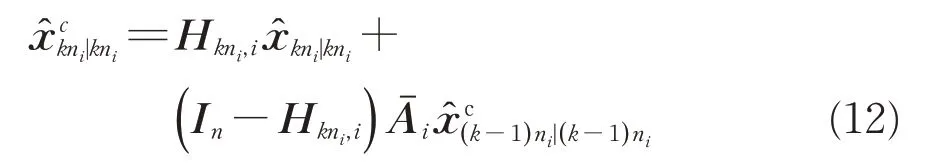
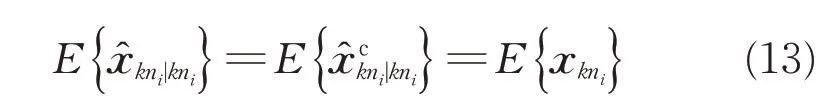
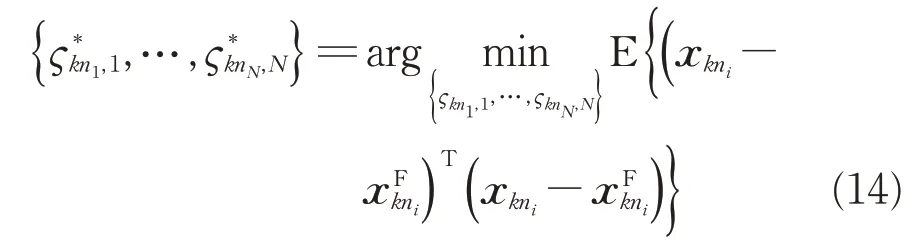
2 融合滤波算法
2.1 局部滤波器的设计
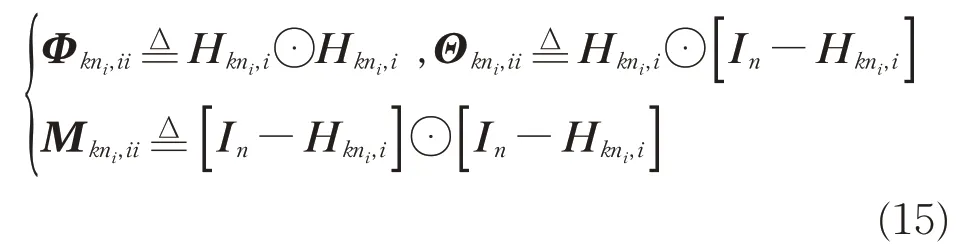
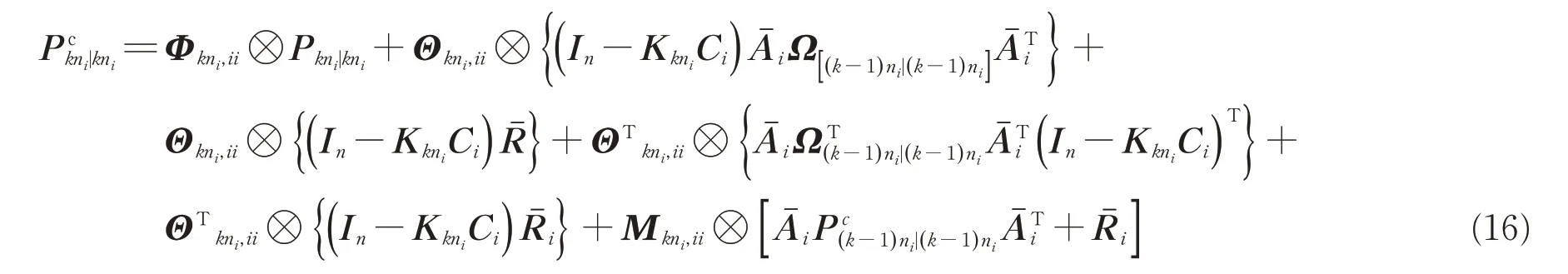
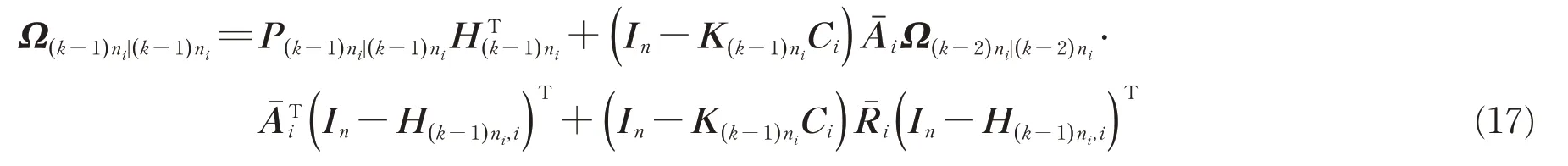
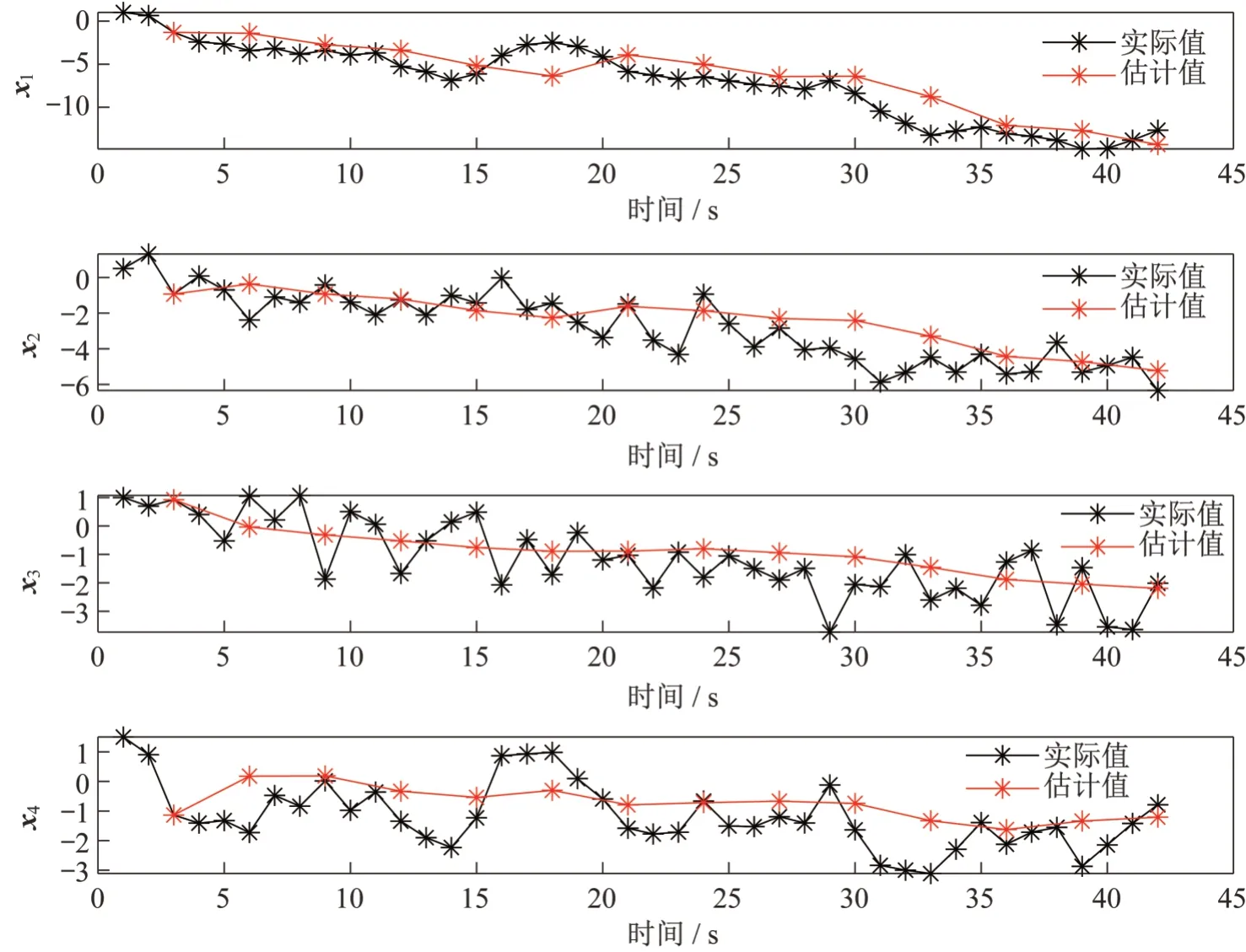
2.2 多速率传感器融合估计
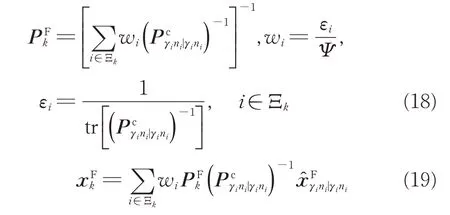
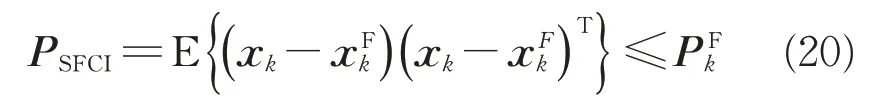
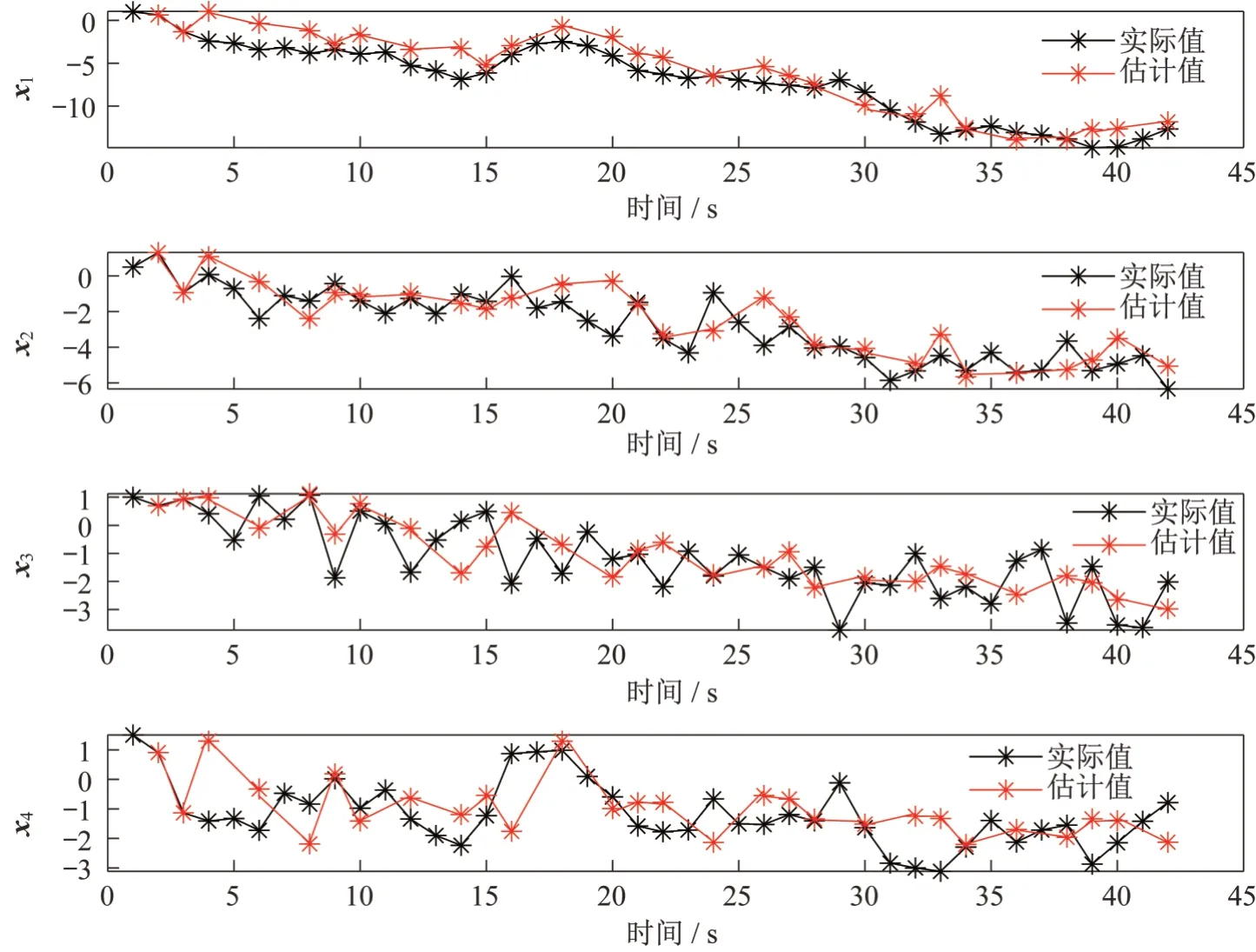
3 仿真实例

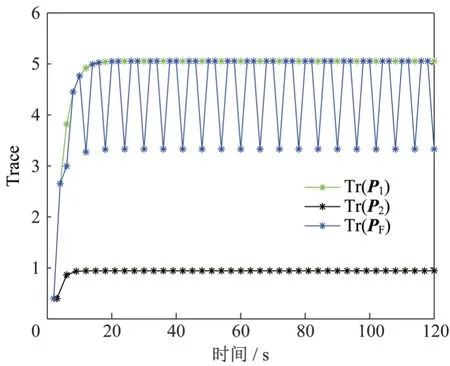
4 结束语
