基于干扰观测器的高马赫数飞行器滑模控制

王家琪，郭建国，郭宗易，赵 斌

（西北工业大学精确制导与控制研究所，陕西西安 710072）

0 引言

高马赫数飞行器是指在20～100 km 的临近空间飞行、最大飞行速度大于5Ma的一类飞行器，飞行速度快、突防能力强、隐蔽性能好［1］，具有极大的军事和民用价值。由于系统内部不确定性和外部环境干扰的存在，高马赫数飞行器的飞行轨迹会受到一定影响［2］。为保证控制系统的控制效果，需要对这些干扰性因素进行充分抑制，使控制系统对内部不确定性和外部环境干扰具有一定的鲁棒性。

在抑制系统内部不确定性和外部环境干扰时，基于干扰观测器的方法得到了广泛应用［3-7］。干扰观测器通过把对控制系统有较大影响的复合干扰估计出来，并在原有标称系统控制器的基础上设计补偿控制器，来抵消复合干扰的影响，提高系统的控制效果［8］。文献［9］针对高马赫数飞行器纵向动态模型，设计干扰观测器来估计参数不确定项，提高了控制精度。文献［10］设计干扰观测器估计外界未知干扰，改善了系统的鲁棒性能。

滑模控制是不连续的非线性控制，对参数不确定性和外部干扰具有较强的鲁棒性［11］。文献［12］设计二阶滑模终端控制器实现对高马赫数飞行器纵向动态模型的速度和高度跟踪。文献［13］结合自学习观测器设计滑模控制器，实现对高马赫数飞行器巡航段速度和高度的稳定跟踪。但是，滑模控制具有一个明显缺点，在控制过程中会发生“抖振”现象［11］，这对控制器的工程实现产生不利影响。本文采用一个非线性函数来替代符号函数，以此来削弱“抖振”现象。同时，为提高收敛速度并抑制干扰，本文改进了传统的指数趋近律，结合干扰观测器设计新型滑模控制律，以改善系统的动态性能，提高系统的鲁棒性。

1 高马赫数飞行器模型分析

1.1 高马赫数飞行器纵向模型

本文采用的高马赫数飞行器纵向模型的数学形式为［14］

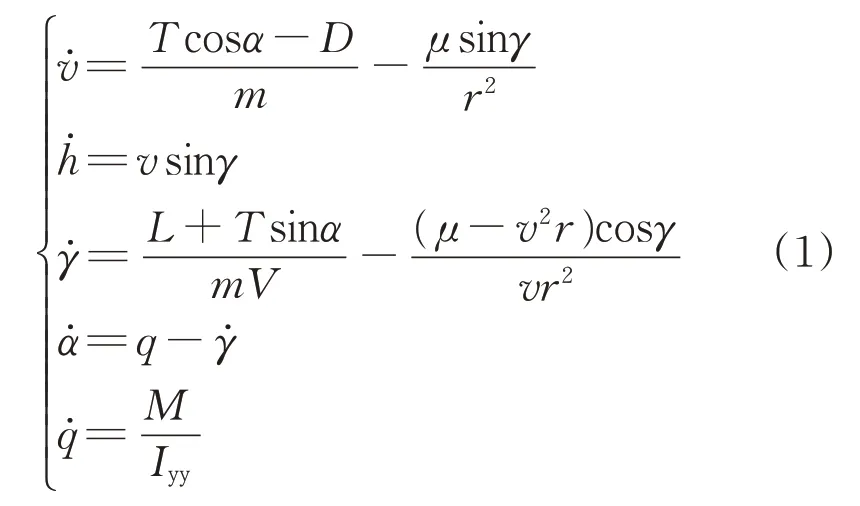
式中：r为飞行器距地心距离；μ为地球引力常数；v、h、γ、α、q分别为高马赫数飞行器的飞行速度、飞行高度、航迹倾角、攻角、俯仰角速度；L、D、T、M分别为升力、阻力、侧向力、俯仰力矩，其具体形式为

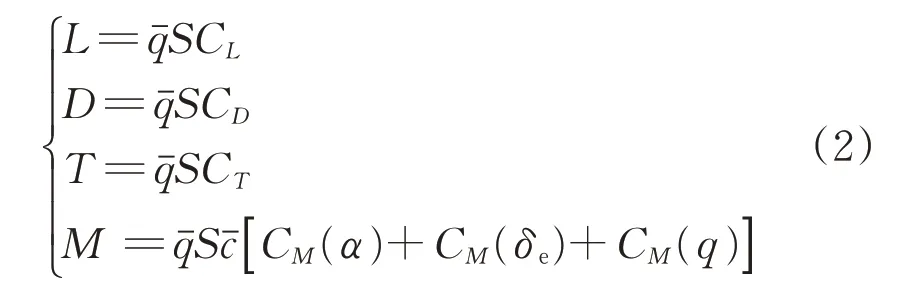
发动机模型数学形式为

式中：β表示油门开度；βc表示控制器输出指令；ωn为自然频率；ξ0为阻尼系数。

1.2 模型转化

将高马赫数飞行器纵向数学模型分解为速度子系统和高度子系统［15］，分别设计干扰观测器和控制器。定义x1=v，x2=h，x3=γ，x4=θp，x5=q，其中θp为俯仰角，满足θp=α+γ。

1.2.1 速度子系统

速度子系统可以表示为

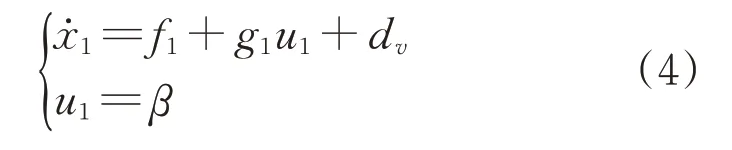
式中：dv表示速度子系统的外部时变干扰；u1为速度子系统的控制输入，表示发动机的油门开度。

当β≥1时，

当β<1时，

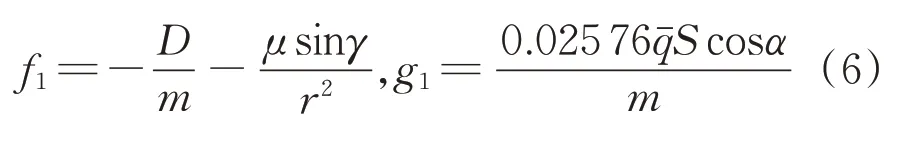
1.2.2 高度子系统

高度子系统可以表示为

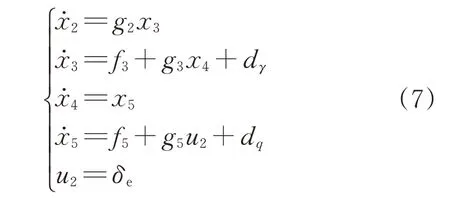
式中：dγ、dq分别表示高度子系统的外部时变干扰；u2为高度子系统的控制输入，表示升降舵偏角；

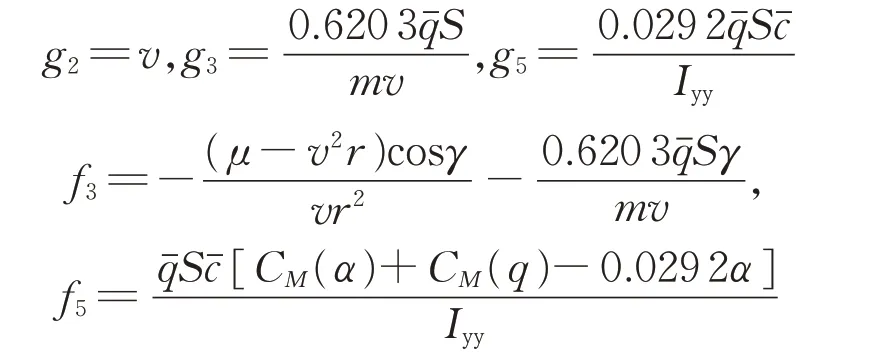
其中，Iyy为转动惯量。

2 干扰观测器设计

由于系统存在不确定性和外干扰，因此引入干扰观测器以提高系统的控制精度。干扰观测器是通过改进状态观测器而得到的一种估计器，用来逼近系统中的不确定性或外干扰，以削弱不确定性或外干扰对系统的影响，提高系统的鲁棒性能。文献［16］针对飞行器模型中的时变干扰设计了一种非线性干扰观测器，用来逼近系统干扰。本文利用该思想，设计速度子系统干扰观测器和高度子系统干扰观测器，分别用来估计速度子系统和高度子系统中的外部干扰，以便于后文控制律的设计。

2.1 速度子系统干扰观测器

速度子系统干扰观测器数学形式为

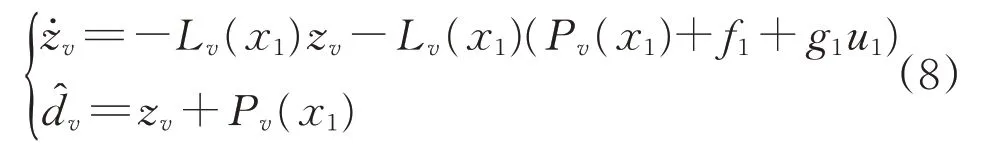
式中：zv为速度子系统干扰观测器的内部状态变量；表示对干扰dv的估计值，是干扰观测器的输出；Pv(x1)是待设计的关于状态x1的非线性函数，其中x1=v是速度子系统的状态变量。在此处是一个正值。通过选择合适的非线性函数Pv(x1)，可以使得干扰估计误差收敛至一个较小范围内，保证干扰观测器的输出逼近干扰dv。

2.2 高度子系统干扰观测器

高度子系统干扰观测器数学形式为

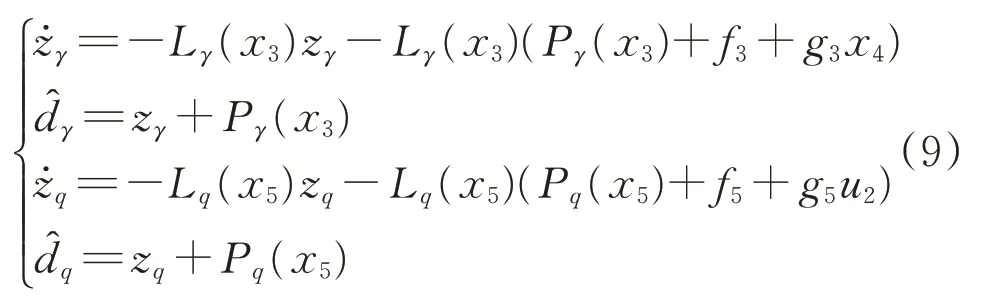
式中：zγ、zq为高度子系统干扰观测器的内部状态变量；分别表示对干扰dγ、dq的估计值，是干扰观测器的输出；Pγ(x3)、Pq(x5)分别是待设计的关于状态x3和x5的非线性函数，其中x3=γ、x5=q均为高度子系统的状态变量；在此处均为正值。通过选择合理的非线性函数Pγ(x3)、Pq(x5)，可以使得干扰估计误差eDO_γ=均收敛至一个较小范围内，保证干扰观测器估计干扰的有效性。

3 滑模控制器设计

通过速度干扰观测器和高度干扰观测器估计出系统中的干扰，用估计值替代实际值，代入到本文设计的控制律中，可以抑制外界未知干扰对系统造成的影响，提高系统的鲁棒性能。基于干扰观测器的控制系统结构如图1所示。图中：xd为输入指令信号；x为系统状态；e为状态跟踪误差；d为系统中的实际干扰；为观测器对干扰的估计值。

图1 含干扰观测器的控制系统结构Fig.1 Control system structure with disturbance observer

控制器的控制目标是通过设置控制输入（升降舵偏转角δe和发动机油门开度β）来控制飞行器的状态输出（速度v和高度h），实现对高马赫数飞行器纵向模型的速度和高度的双重跟踪控制［17］。下面分别设计速度控制器和高度控制器。

3.1 速度子系统

3.1.1 速度控制器设计

定义滑模面为

对式（10）求导可得

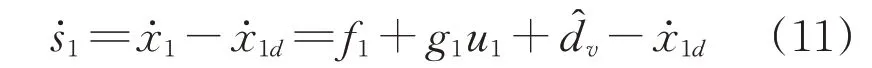
滑模控制中通常采用传统的指数趋近律

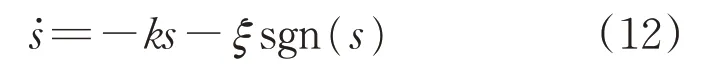
式中：k、ξ为指数趋近律的系数，均为常值。

本文设计一种经过改进的趋近律，即

这种经过改进的趋近律和传统指数趋近律相比，幂次更高，收敛速度更快，同时也能保证系统稳定。

将式（13）代入式（11）可得速度子系统控制律为

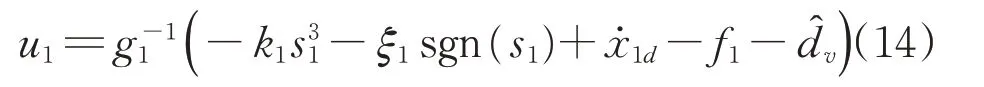
3.1.2 稳定性分析

取Lyapunov函数为

对式（15）求导可得

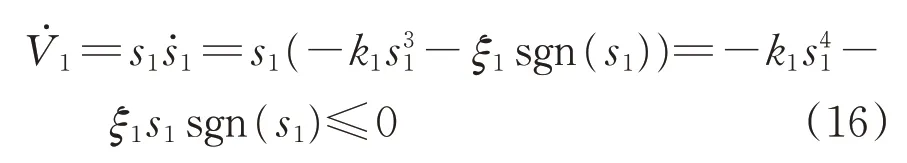
从而有

显然，速度子系统的闭环控制器是渐近稳定的。

3.2 高度子系统

3.2.1 高度控制器设计

高度控制器结合反步法的设计思想，采用动态面控制，具体设计如下。

定义误差

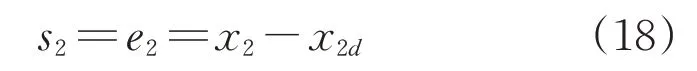
对式（18）求导可得

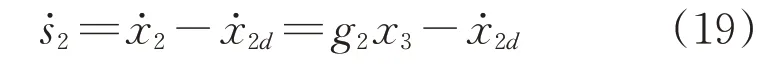
为提高收敛速度，设计经过改进的趋近律

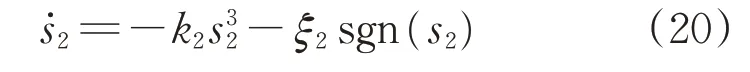
将式（20）代入到式（19）可得虚拟控制量

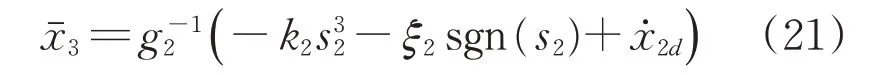
采用动态面方法，设计低通滤波器得到x3d，即

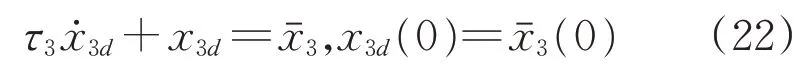
类似地，定义误差

可得虚拟控制量

设计低通滤波器得到x4d，即

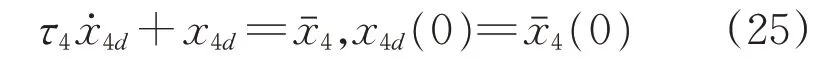
类似地，定义误差

可得虚拟控制量

设计低通滤波器得到x5d，即

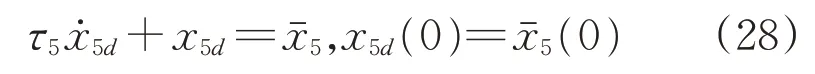
同样地，定义

可得最终控制输入为

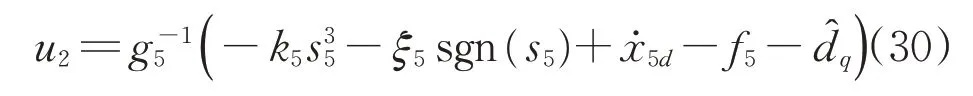
为削弱滑模控制中的“抖振”问题，采用如下非线性函数替代虚拟控制量和最终控制输入中的符号函数［18］：

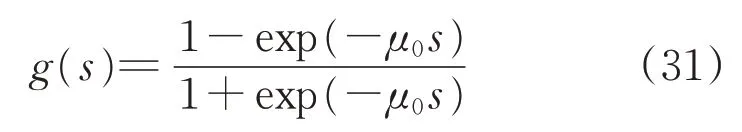
式中：μ0是一个正参数，通过引入该非线性函数可以有效避免滑模控制中符号函数驱动引起的“抖振”现象，从而提高控制效果。

3.2.2 稳定性分析

取Lyapunov函数为

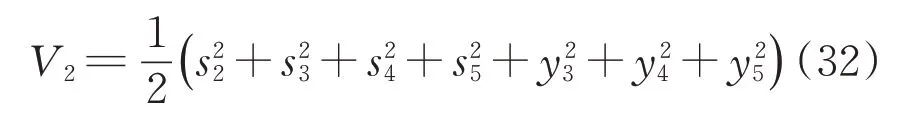
对V2求导可得

式中：ε为任意小的正常数；τi(i=3～5)为各个滤波器系数。

整理可得

按如下条件设计参数：

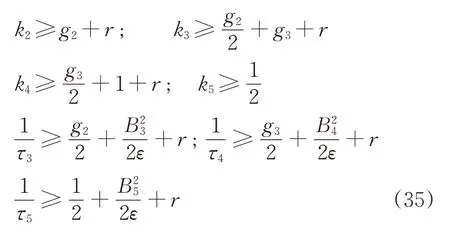
式中：r为待设计的参数。

就有

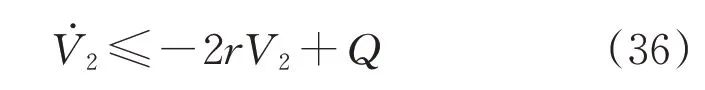
对不等式（36）求解，可得

那么就有

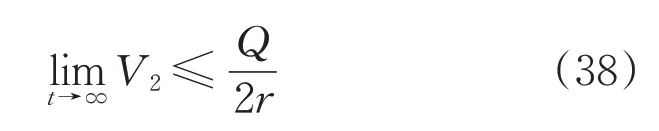
显然，高度控制器的闭环系统是有界稳定的，可以收敛至一个较小范围内。

4 仿真验证

为验证本文方法的有效性，在MATLAB 环境下对高马赫数飞行器纵向动态模型仿真验证，本文的高马赫数飞行器模型数据选自文献［13］。

考虑系统存在时变正弦干扰，分别在无干扰观测器、采用传统指数趋近律并使用干扰观测器、采用改进趋近律并使用干扰观测器3 种情况下进行仿真，可以得到如图2～4所示的仿真结果。

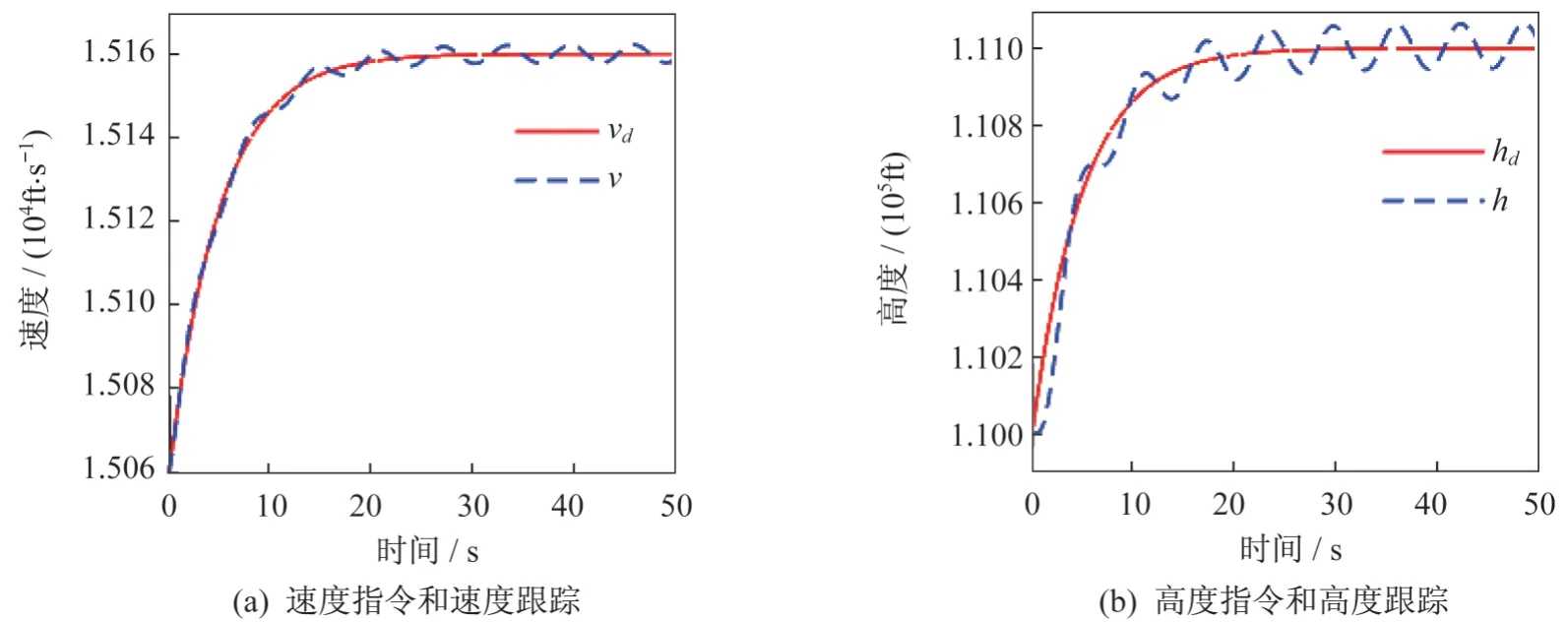
图2 无干扰观测器时的系统仿真结果Fig.2 Simulation results of the system without interference observer

由图2可知，当系统存在时变干扰时，速度和高度跟踪曲线有明显的误差，控制系统的精度达不到系统要求。由图3 和图4 可知，干扰观测器对外部干扰具有良好的估计效果，减少了外界不确定性对高马赫数飞行器带来的影响，提高了系统的鲁棒性能。同时，速度和高度能在干扰存在的情况下较好地跟踪指令信号，保障了飞行器的飞行性能。值得注意的是，在使用经改进的趋近律时，收敛速度明显提高，很好地改善了系统的动态性能，这充分说明：与传统指数趋近律相比，经改进的趋近律效果更好。

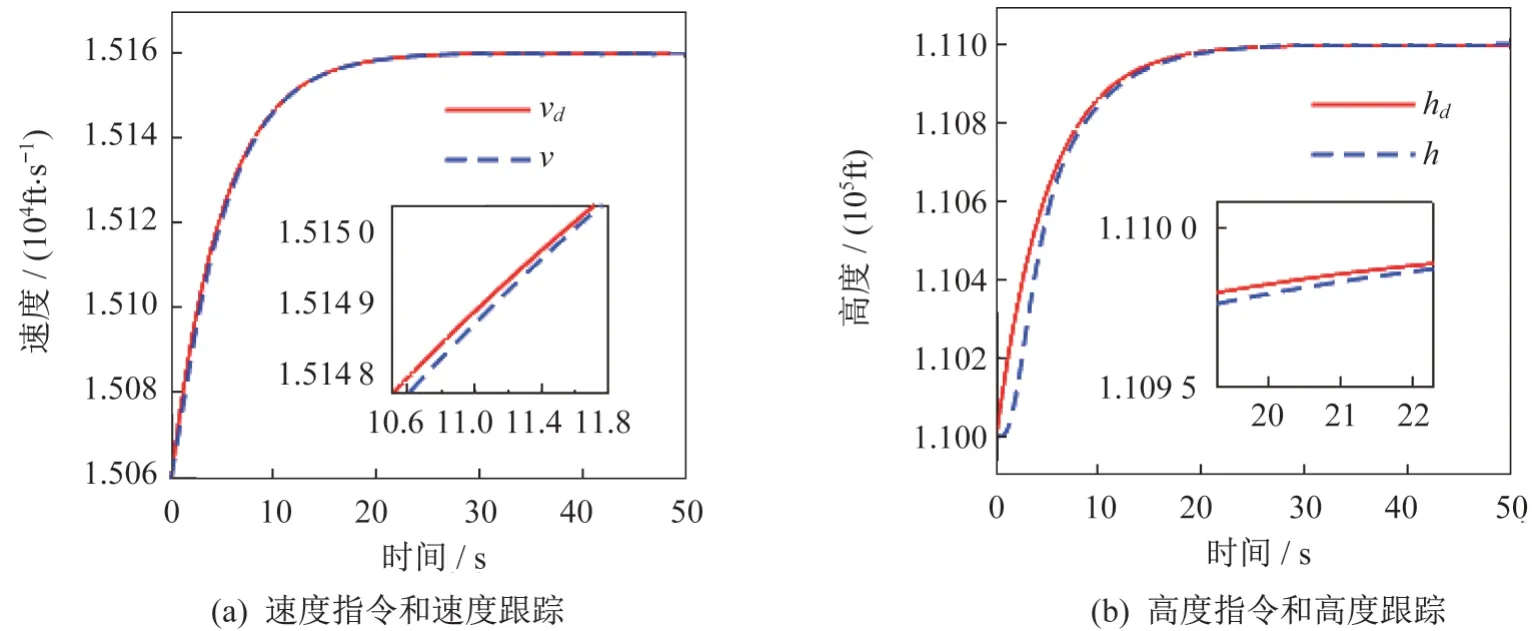
图3 有干扰观测器并采用传统趋近律时系统仿真结果Fig.3 System simulation results with disturbance observer and traditional approach law

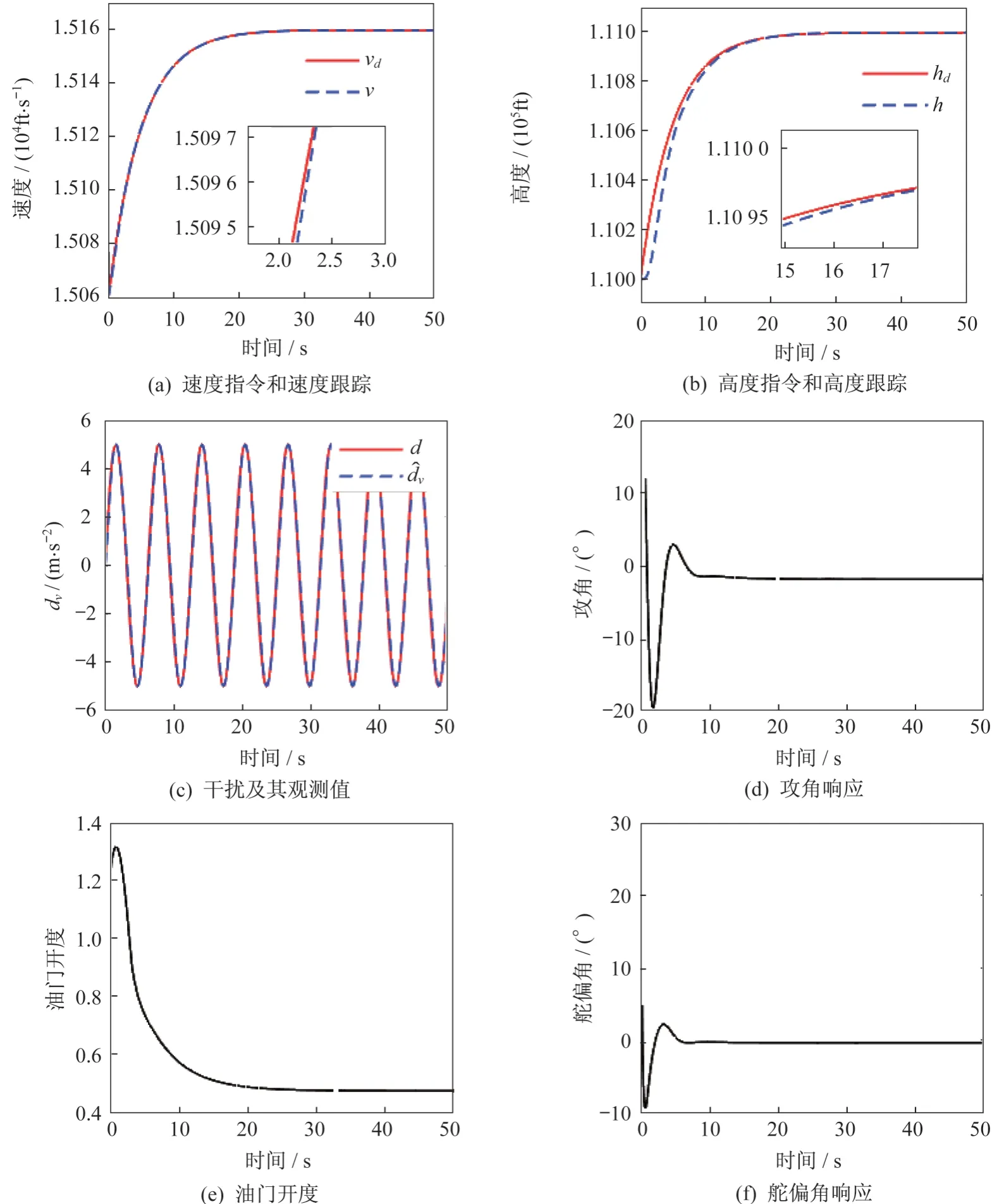
图4 有干扰观测器并采用改进趋近律时系统仿真结果Fig.4 System simulation results with disturbance observer and improved approach law

5 结束语

本文设计干扰观测器来估计高马赫数飞行器纵向模型中的外部干扰，结合滑模动态面控制器实现了对巡航段高马赫数飞行器速度和高度指令的稳定跟踪。本文提出了一种改进滑模趋近律，提高了系统的收敛速度，改善了系统的动态性能；使用一个连续的非线性函数替代符号函数，削弱了滑模控制中的“抖振”问题；采用干扰观测器估计和补偿干扰，提高了系统的鲁棒性。