滑翔飞行器气动外形与轨迹一体化设计优化

2021-09-16陈永信

空天防御 2021年3期

陈永信

（上海机电工程研究所，上海 201109）

0 引言

滑翔飞行器通常需要通过动力装置达到一定飞行高度和速度，而后依靠自身气动升力进行无动力飞行［1］。该类飞行器的飞行速度高、机动范围大且突防生存能力强，可应用于远程物资的快速运送或精确打击任务，具有重要的经济和军事价值［2］。

与传统飞行器相比，滑翔飞行器的飞行环境更为严酷，约束条件更为严格，因此在该类飞行器的总体设计中，各学科更加紧密耦合［3］。传统总体设计方法采用解析公式、经验数据或简化的学科模型进行分析，难以体现多学科耦合因素的影响，在多约束条件下获得可行优化解的难度大［4］。多学科设计优化（multidisciplinary design optimization，MDO）方法可充分考虑多学科间的耦合效应，近年来成为航空航天领域的研究热点［4-7］。但是MDO 方法中往往涉及耗时长的学科分析和大量的设计变量，直接进行总体设计优化的难度极高且计算时间成本巨大，优化效果通常并不理想，甚至难以获得可行解［8］。代理优化方法能够有效针对优化难度高且耗时长的问题，成为MDO研究中的关键技术［8-10］。目前代理优化方法多应用于涉及学科较少的设计优化问题中，例如飞行器气动外形设计优化［8，10-12］、结构设计优化［13-14］等，对于滑翔飞行器与轨迹一体化设计优化的相关研究尚较少。

本文针对滑翔飞行器与轨迹一体化设计优化问题，建立飞行器无动力纵向运动方程和主要的飞行约束模型；为获得飞行器的气动特性参数，建立滑翔飞行器的气动外形参数化模型，并采用非结构三角形面元法和流线追踪技术实现考虑黏性影响的气动特性计算；采用自适应伪谱法获得多约束条件下飞行器的最大航程及最优轨迹；基于Kriging代理模型和多采样点高效全局优化算法提升一体化设计优化问题的求解效率，实现滑翔飞行器与轨迹一体化设计优化，并对计算结果进行分析。

1 问题描述

1.1 优化问题

针对尾部采用全动空气舵进行姿态控制的面对称升力体式滑翔飞行器，其初始飞行条件确定，通过一体化设计优化滑翔飞行器的气动外形参数和飞行轨迹，在满足飞行器外形尺寸、容积率和飞行过程中主要约束的情况下，提升飞行器滑翔飞行段的最大航程能力。

1.2 飞行器纵向运动方程

关注飞行器的航程能力，为了方便描述滑翔飞行器的运动特性，基于瞬时平衡假设，考虑地球为无旋转圆球，建立极坐标形式下无动力无侧滑的飞行器纵向运动方程为

式中：h、v、λ、s为状态变量，分别代表飞行器的飞行高度、速度、航迹角和航程；m为飞行器的质量，飞行过程中保持不变；引力常数μE=3.986×1014m3/s2；地球半径Re=6 378 137 m；FLb和FDb分别为飞行器所受的配平升力和配平阻力，可表示为

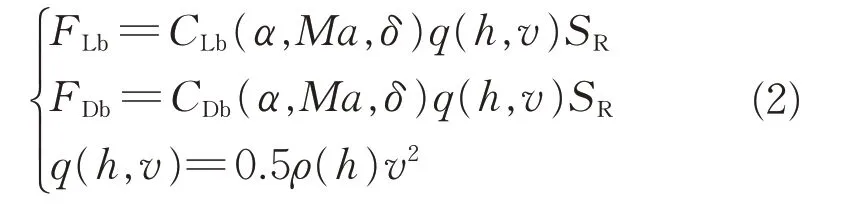
式中：CLb和CDb分别为飞行器的配平升力系数和配平阻力系数，由气动外形和飞行状态共同决定；α、Ma和δ为分别为飞行器的迎角、马赫数和俯仰舵偏角；SR为参考面积；q为飞行器的动压；ρ为大气密度，由飞行高度h决定，本文采用美国1976 标准大气模型［15］进行计算。

1.3 飞行约束条件

1.3.1 俯仰力矩配平约束

初步设计阶段，仅考虑飞行器的静态俯仰力矩配平能力，对配平俯仰舵偏角进行限制，并留有一定余量，即

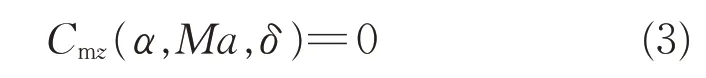
式中：Cmz为飞行器的俯仰力矩系数。对于给定的迎角α和马赫数Ma，需要通过数值迭代求解式（3）获得δ，则俯仰力矩配平约束可表示为

另一方面为减轻姿态控制系统的压力，还需要对迎角变化速率进行限制，即

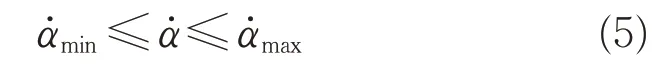
在轨迹设计优化中，为了方便地描述控制约束，将式（1）中的状态变量扩展为x=［h，v，λ，s，α］T，并将作为轨迹设计中待优化的控制变量u，即

1.3.2 能量管理约束

为保证飞行器在滑翔段末端的能量管理要求，需要对末端的飞行高度和速度进行限制

式中：tf为滑翔段的末端时刻；hf和vf为滑翔段的末端高度和速度。

1.3.3 飞行过程约束

飞行器在大气层内高速飞行，其载荷环境严酷，需要考虑飞行器的防热、结构强度等约束，因此对飞行过程中飞行器的驻点热流密度、法向过载ny和动压q进行限制，即

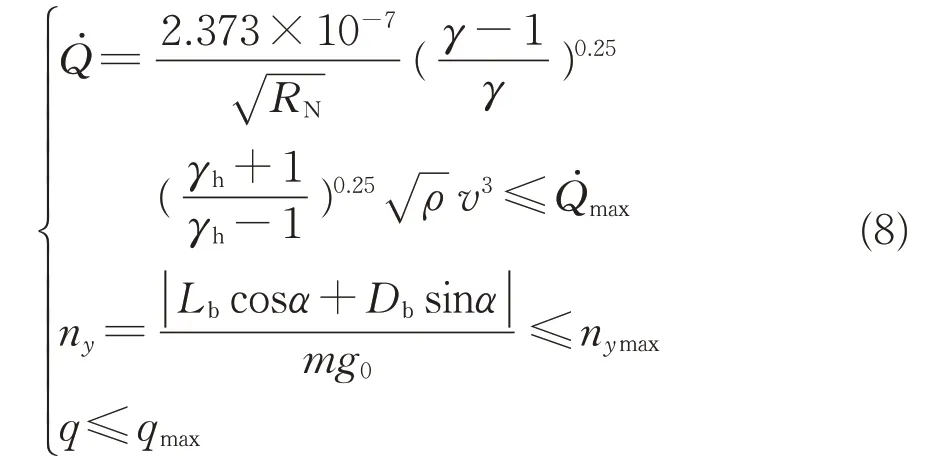
式中：RN为驻点曲率半径；完全气体比热比γ=1.4，高温气体比热比γh=1.2；海平面引力加速度g0=9.806 6 m/s2。

2 滑翔飞行器气动特性计算

2.1 滑翔飞行器气动外形参数化建模

基于类型函数/形状函数的几何参数化建模方法（class function/shape function transformation technique，CST）具有控制参数少且外形表达丰富的优点［16］，近年来在飞行器气动外形参数化建模中得到了广泛的应用［17-19］。通常参数化曲线方程可以统一表示为

式中：x、y和z为三维外形表面的物理坐标分量；ξ，η∈［0，1］为轴向归一化变量；L0为三维外形的轴向特征长度，H0为曲线特征高度，W0为曲线特征宽度；C为类型函数；S为形状函数，通常采用Bernstein 多项式或B样条函数表示［20］；H为厚度函数。由式（9）可知，对于三维外形沿轴线方向的任意截面，其形状类型和大小由轴向和横向变量共同控制决定。因此，该方法可通过选择不同的类型、形状和厚度函数来获得丰富的三维外形。

本文以文献［19］中的面对称升力体构型为基础进行设计优化，该类升力体外形示意图见图1。

采用式（9）形式对图1 中的升力体外形进行参数化表达，其参数化方程为

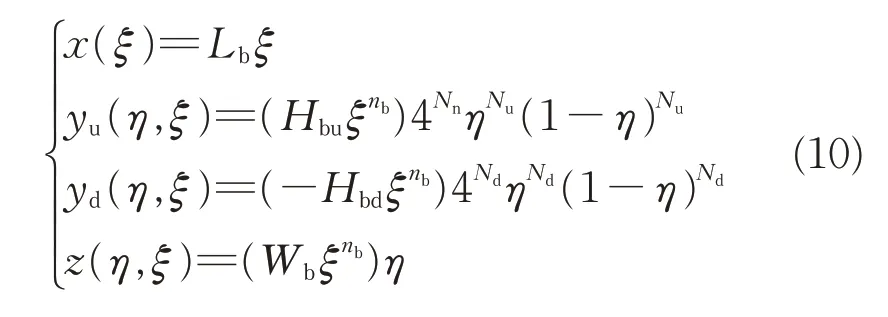
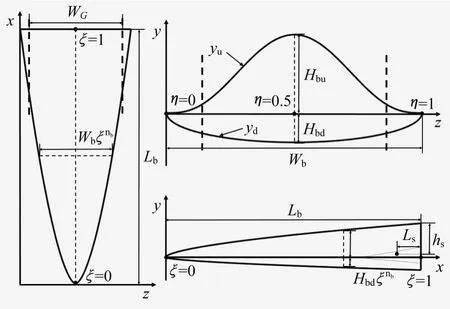
图1 升力体外形示意图Fig.1 Schematic diagram of lifting body shape

式中：Lb为升力体的长度；Wb为底部截面的宽度；nb为升力体俯视面轮廓幂指数；yu和yd分别为升力体上和下表面的高度坐标；Hbu和Hbd分别为底部截面上和下轮廓曲线的最大高度；Nu和Nd分别为底部截面上和下轮廓曲线的形状函数指数。

升力体尾部配置全动空气舵以进行飞行器姿态控制，其几何外形见图2。

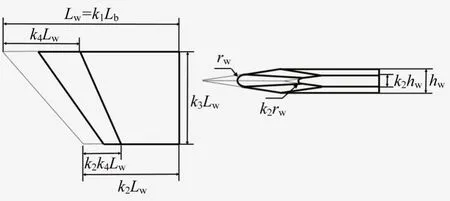
图2 空气舵外形示意图Fig.2 Schematic diagram of air rudder shape

图2中：Lw为舵面前缘未钝化时的根弦长度，比例参数k1=Lw/Lb，用来控制根弦长度；hw为舵面后缘厚度，由结构载荷学科确定；rw为舵面前缘钝化半径，由气动防热学科确定；k2、k3和k4为比例参数，其中k2用来控制根梢比和后掠角，k3用来控制展弦比，k4用来控制舵面前缘的倾角。

为了安装如图2所示的全动空气舵，需要对升力体尾部进行削平，见图1。图1 中WG为升力体削平后的宽度；Ls和hs为全动空气舵的舵轴安装位置参数。另一方面，考虑到滑翔飞行器头部驻点的防热要求，需要对头部进行钝化，定义钝化半径为rG，由气动防热要求确定。为了保证头部区域的外形光滑且连续，需要对球头与升力体连接处进行平滑过渡。此外，考虑到滑翔飞行器的内部需要装载一定仪器部件和有效载荷，因此总体设计对飞行器的容积率RV提出要求，其定义为

式中：VL为削平后升力体的体积；SL为削平后升力体在xz平面的投影面积。

2.2 滑翔飞行器气动特性计算

本文采用非结构三角形面元法和流线追踪技术实现考虑黏性影响的气动特性计算，具体计算方法见文献［21］，本文不再赘述。对于倾斜转弯（back-toturn，BTT）控制的面对称滑翔飞行器，无侧滑角，即侧向力系数为0，因此，当获得考虑黏性修正的升力系数CLb和阻力系数CDb，并给定参考坐标系下的飞行器质心后，飞行器绕质心的气动力矩系数可表达为

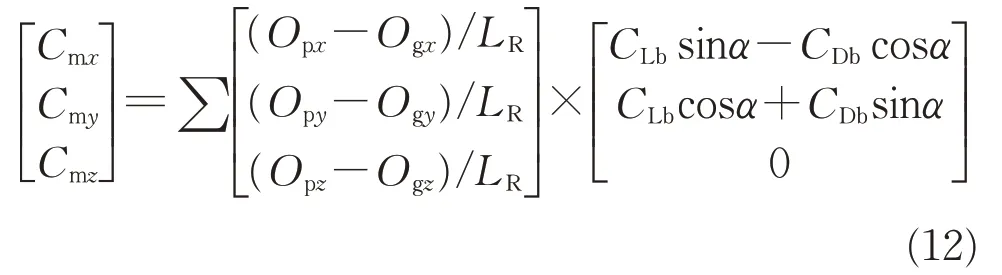
式中：Cmx、Cmy、Cmz分别为飞行器绕质心的滚转、偏航和俯仰力矩系数；Opx、Opy、Opz分别为参考坐标系下各三角形面元中心的坐标分量；Ogx、Ogy、Ogz分别为参考坐标系下飞行器质心的坐标分量；LR为飞行器的参考长度。

3 滑翔飞行器最大航程计算

当滑翔飞行器的质量和气动特性确定后，其最大航程计算问题可描述为一个具有多种约束条件的连续时间最优控制问题（continuous-time optimal control problem，COCP），即

式中：Eq.（1）（6）为式（1）和（6）组成的微分约束；Eq.（4）（5）（7）（8）为式（4）、（5）、（7）和（8）组成的不等式约束。

对于形如式（13）这类的多约束COCP，可采用自适应Legendre-Gauss-Radau（LGR）伪谱法进行有效的离散求解［22］。本文采用文献［22］中基于Legendre 近似理论的自适应算法，并引入配点区间缩减技术［22］，该算法相比于传统算法具有更高的求解效率和稳健性。

4 基于代理优化的滑翔飞行器设计优化

4.1 Kriging代理模型

Kriging 代理模型的预测精度高，且能够提供目标预测值的平均标准差信息，因此被广泛应用于代理优化中［8］。其假设目标函数为高斯静态随机过程的具体实现，可表示为

式中：f（X）为目标函数，X为f（X）的输入变量；B（X）为回归基函数矩阵，b为回归系数矩阵，BT（X）b代表f（X）的数学期望；G（X）为高斯静态随机过程，其均值为0，方差为σ2，且对于不同的输入变量Xi和Xj，随机变量间存在相关性，由相关函数R描述。R随Xi和Xj间距离的增大而减小，且满足：|Xi-Xj|=0 时，R=1；|Xi-Xj|→∞时，R=0。R的表达式为

式中：nx为输入变量的维数；下标k代表输入变量第k维所对应的参数；Rk为相关基函数。

Kriging 代理模型利用已计算的ns个输入变量（样本点）处的目标函数值进行线性加权，根据无偏估计要求，采用拉格朗日乘子法推导获得均方差MSE最小的权重系数，从而利用插值来预测未知输入变量处的目标函数估计值，则最优目标函数估计值的表达式为

式中：ω（X）为权重系数矩阵；fs为样本点的目标函数值列向量；r（X）为预测点的相关函数列向量；Bs和Rs分别为样本点的回归基函数和相关函数矩阵。

式（16）可以化简为式（14）的形式，即为

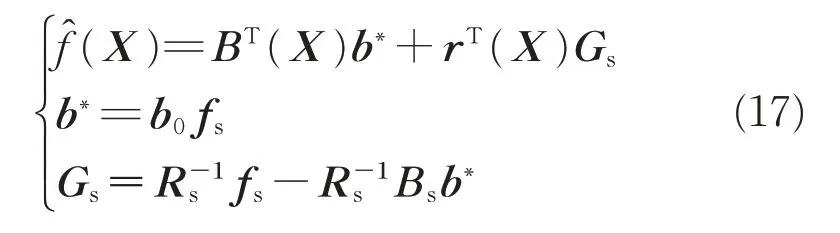
根据式（17）可以发现，b*和Gs仅取决于样本点，因此对预测点的目标函数值进行预测时，仅需计算预测点的B（X）和r（X）。上述插值预测的计算耗时相对于原分析模型的计算耗时可以忽略不计。此外，预测点处目标函数值的平均标准差估计值为

回归基函数和相关基函数的选择对Kriging 代理模型的预测精度和算法鲁棒性有较大影响。本文中回归基函数选择为一阶回归函数，相关基函数选择为各向异性的指数高斯函数，其控制参数较多，能够有效改善Kriging 模型的鲁棒性［8］。则相应模型的表达式为

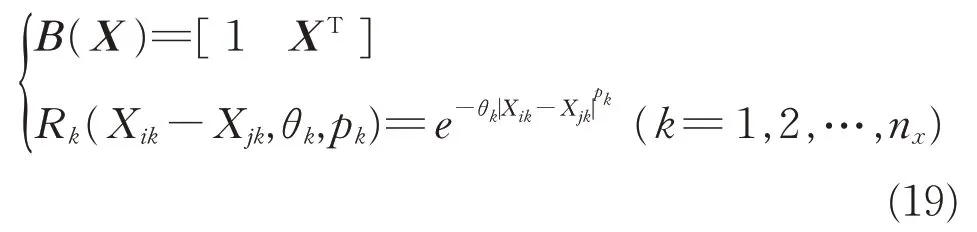
式中：θk和pk（1≤pk≤2）为模型训练超参数。

根据“极大似然估计”准则，可建立无约束优化问题来确定2nx个模型训练超参数，则优化问题为

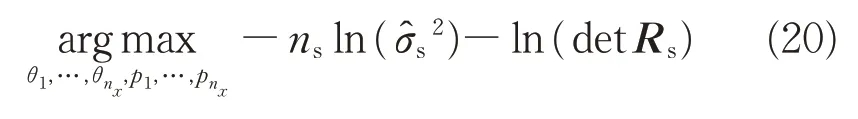
4.2 代理优化算法

序列代理优化（sequential surrogate-based optimization，SSBO）算法是一类求解高计算成本优化问题的算法，该算法首先采用较少的样本点建立初始代理模型代替计算成本很高的目标函数或约束函数，并求解代理优化问题，当求解结果不满足求解要求时，按一定准则加入新样本点来重构代理模型，并重复进行优化直至结果满足求解要求。

加点准则是序列代理优化算法的核心［11］，对于基于Kriging代理模型的代理优化算法，目前广泛采用的加点准则主要包括：最小目标函数预测值（minimum predicted-value，MP）加点准则、最大目标函数值改善期望（expected improvement，EI）加点准则等。其中高效全局优化（efficient global optimization，EGO）算法即采用EI加点准则［23］。

对于约束优化问题，MP 准则通过求解约束优化问题（21）获得新样本点［11］，EI准则通过求解约束优化问题（22）获得新样本点［23］，即

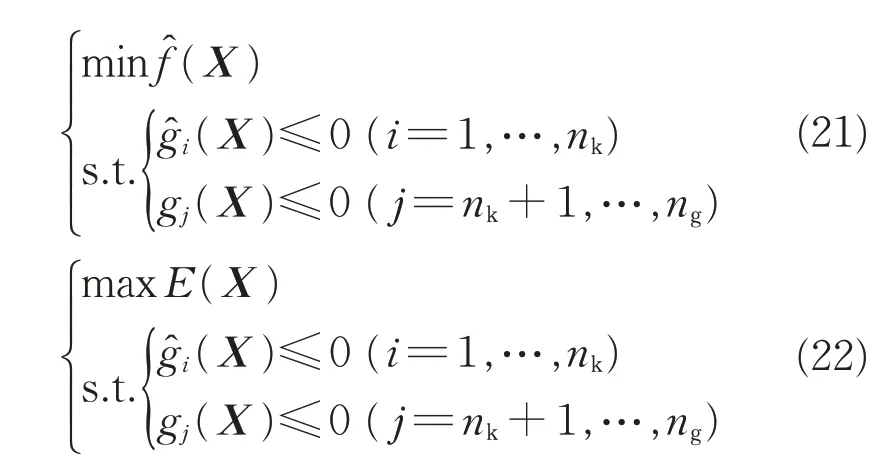
式中：nk为采用代理模型的约束数量；ng为约束的总数量为第i个约束gi（X）的代理模型；E（X）为目标函数值改善的期望，其表达式为

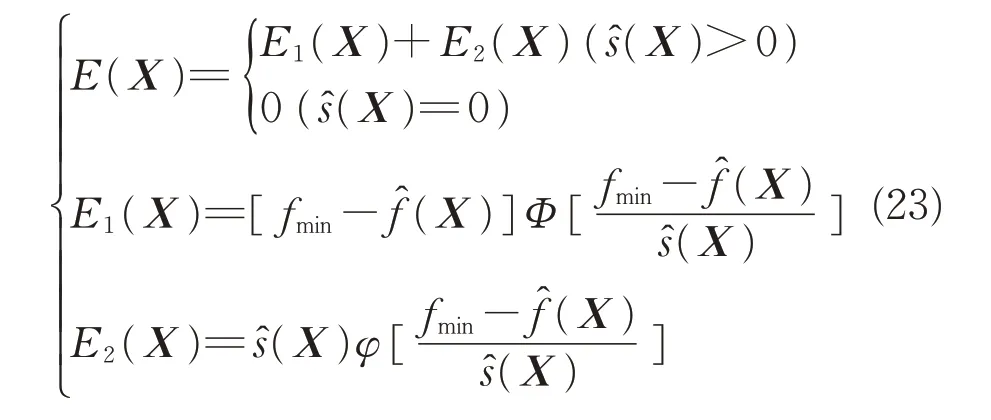
式中：fmin为当前样本点中目标函数真实值的最小值；Φ为标准正态累积分布函数；φ为标准正态概率密度函数。

MP 准则具有较好的局部收敛性，但容易收敛至局部最优解［11］；EI 准则具有全局收敛性，但局部收敛速度较慢［23］。因此，为使得序列代理优化算法兼具一定全局和局部搜索能力，本文在每次迭代过程中，在原样本点集中同时加入MP 准则和EI 准则获得的两种样本点来重构Kriging代理模型，并称算法为多采样点高效全局优化算法（multi-sampling efficient global optimization，MEGO）。MEGO 算法的迭代收敛条件为

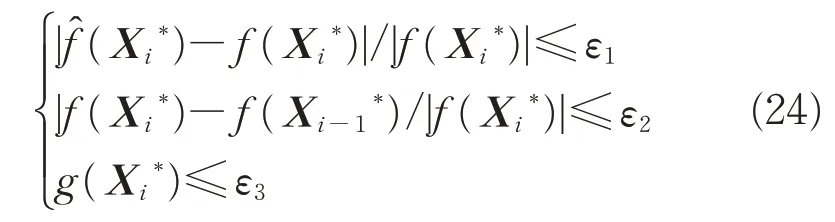
式中：ε1、ε2和ε3分别为相对误差精度、代理模型精度和约束满足精度；为第i次序列代理优化的最优解。

4.3 滑翔飞行器气动外形与轨迹一体化设计优化

在MEGO算法中，为了降低初始采样时样本点间的相关性，以提高Kriging 代理模型的近似精度，本文采用优化拉丁超立方体试验设计（optimal latin hypercube design，OLHD）算法［24］在设计空间内生成10nx个初始样本点。对于式（21）和（22）的约束优化问题，本文采用遗传算法（genetic algorithm，GA）和序列二次规划（seqential quadratic programming，SQP）算法的组合算法进行求解，以避免陷入局部最优解。

对于本文滑翔飞行器气动外形与轨迹一体化设计优化问题，采用MEGO算法的求解流程见图3。

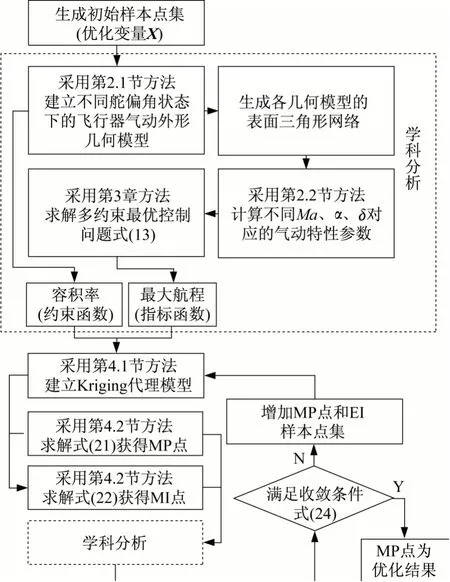
图3 MEGO算法流程Fig.3 Algorithm flow of MEGO method

5 仿真校验

5.1 仿真环境

本文基于PYTHON 语言驱动ABAQUS 软件，实现滑翔飞行器气动外形参数化建模和非结构三角形表面网格的自动化划分；基于MATLAB R2019b 平台编写气动特性计算模块、自适应LGR伪谱法轨迹优化模块以及代理优化模块程序，采用SNOPT 软件包求解非线性规划（nonlinear programming，NLP）问题；计算环境为Windows 10 2.60GHz，16.0 GB内存。

5.2 仿真结果

本文中滑翔飞行器的质量m为固定值，假设其质心在纵轴上，并定义质心到头部顶点的距离与飞行器长度Lb的比值为质心位置系数k0。本文优化变量X=［Lb，nb，Hbu，Hbd，Nu，Nd，k0，k1，k2，k3，k4］，包括10 个滑翔飞行器气动外形参数以及位置质心系数，优化设计变量的搜索范围设置见表1。

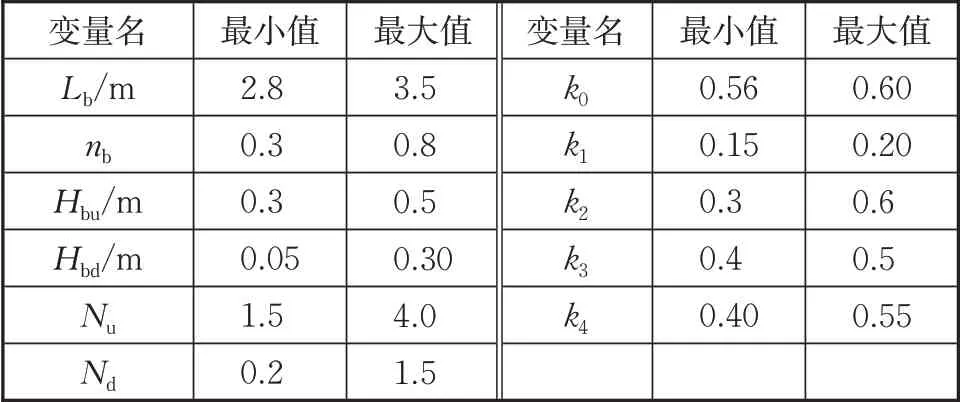
表1 优化变量搜索空间Tab.1 Searching space of optimization variables

其他气动外形参数则根据发射平台几何尺寸、结构载荷和热防护等要求预先确定为固定值，其中包括：Wb=1.1 m，WG=0.9 m，rG=0.03 m，rw=0.003 m和hw=0.02 m。空气舵舵轴安装位置参数设置为：Ls=0.51Lw和hs=Hbu。在气动特性计算时设置：SR=0.151 8 m2和LR=Lb。滑翔飞行器飞行初始条件和约束边界参数为固定值，且，相应参数的设置见表2。

表2 飞行初始条件和约束定义Tab.2 Definition of flight initial conditions and constraints

为了分析滑翔飞行器容积率与最大航程的关系，本文分别对10 种不同容积率约束RV≥RVmin的情况进行了求解，其中RVmin分别取0.24、0.26、0.28、0.30、0.32、0.34、0.36、0.38、0.40 和0.42。MEGO 算法的收敛精度设置为：ε1=ε2=ε3=0.001。滑翔飞行器气动外形与轨迹一体化设计优化结果见图4～13。为了验证MEGO 算法的有效性，采用EGO 算法作为对比算法，对相同问题进行求解，算法性能对比结果见表3，表中：Rf为优化结果相对基准方案提升的百分比；Nf为图3中学科分析模块的调用次数。其中基准方案选择为初始样本点中满足全部约束条件的最优点。

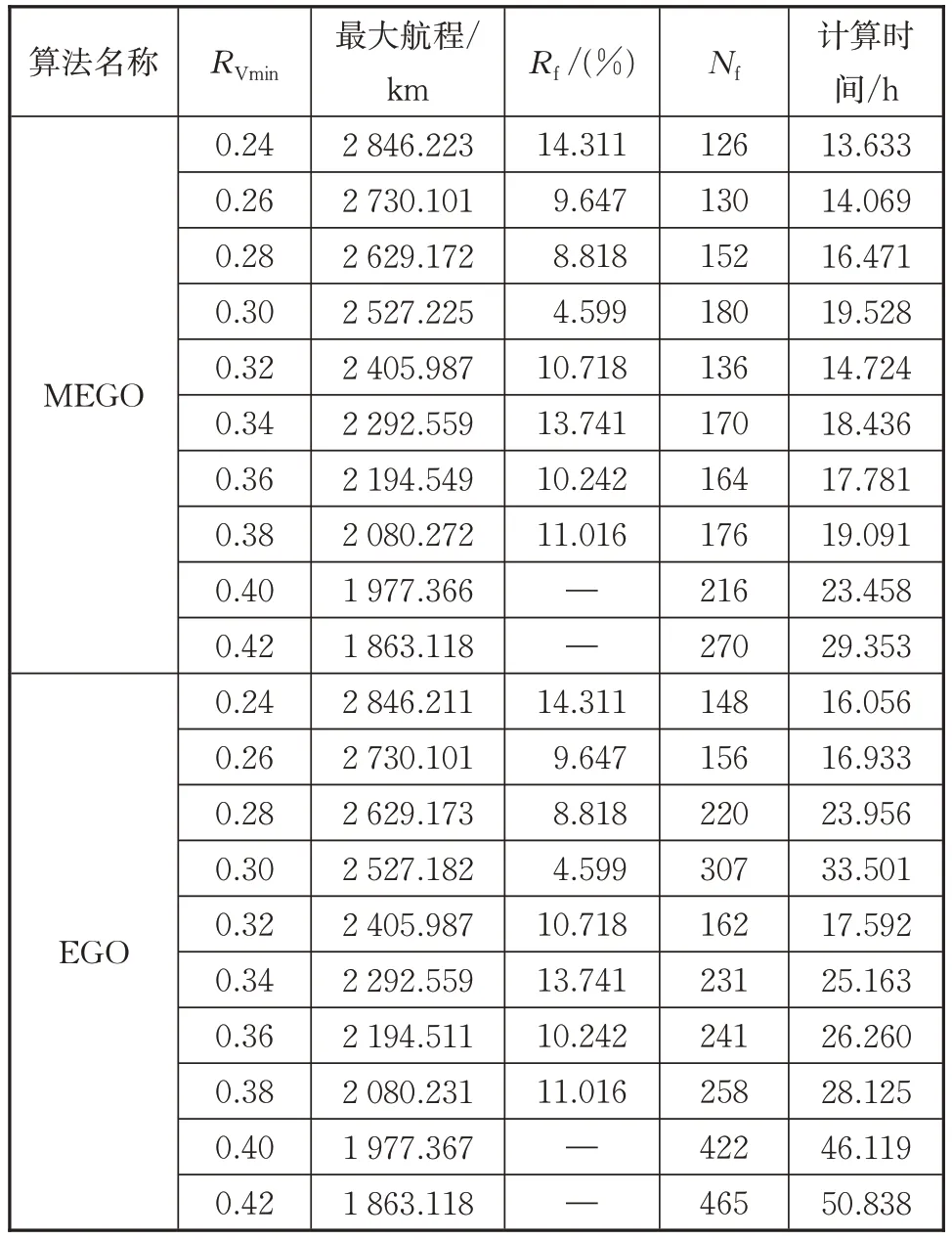
表3 不同算法的优化结果Tab.3 Optimization results of different methods

由图4 和5 可知，优化结果中飞行器末端飞行高度和速度均满足端点约束要求。由图7～10 可知，整个飞行过程中，最大迎角变化率不超过2（°）/s，即迎角变化平缓，满足约束要求；热流密度、法向过载和动压均满足过程约束要求，其中最大热流密度均达到5 500 kW/m2的约束边界值，即热流密度为本文滑翔飞行器最大航程的限制因素。由图11可知，俯仰力矩系数均不大于4×10-4，满足配平精度要求。俯仰舵偏角配平约束限制了飞行器的可用配平迎角，由图12可知，在考虑常值干扰俯仰力矩系数后，整个飞行过程中的配平俯仰舵偏角仍能满足约束要求，即设计优化结果具有一定鲁棒性。

图4 高度与航程Fig.4 Altitude versus range

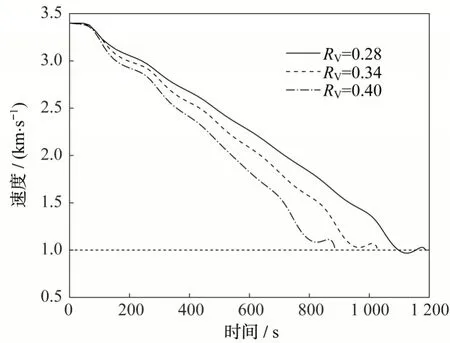
图5 速度与时间Fig.5 Speed versus time

图6 迎角与时间Fig.6 Angle of attack versus time

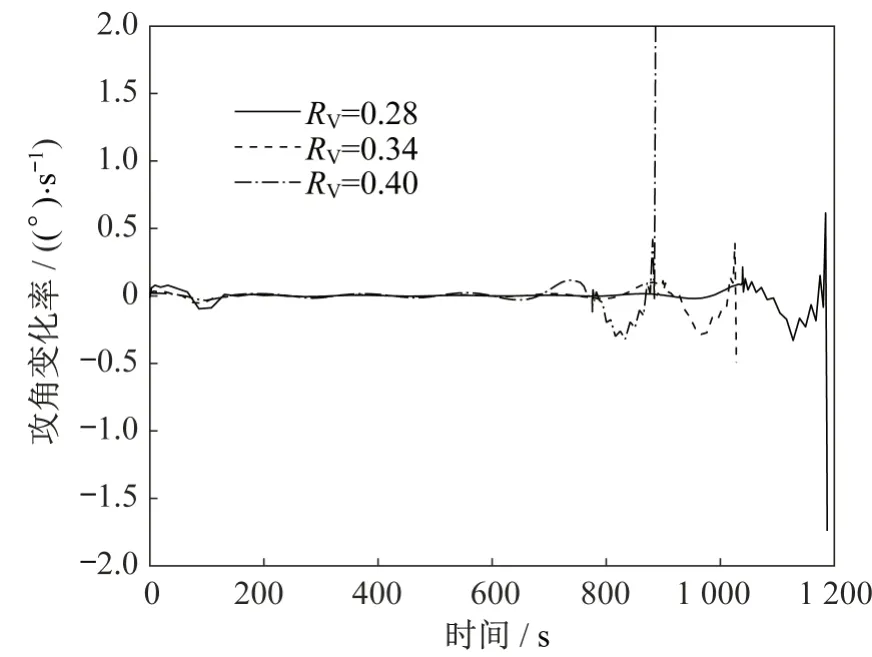
图7 迎角变化率与时间Fig.7 Change rate of angle of attack versus time

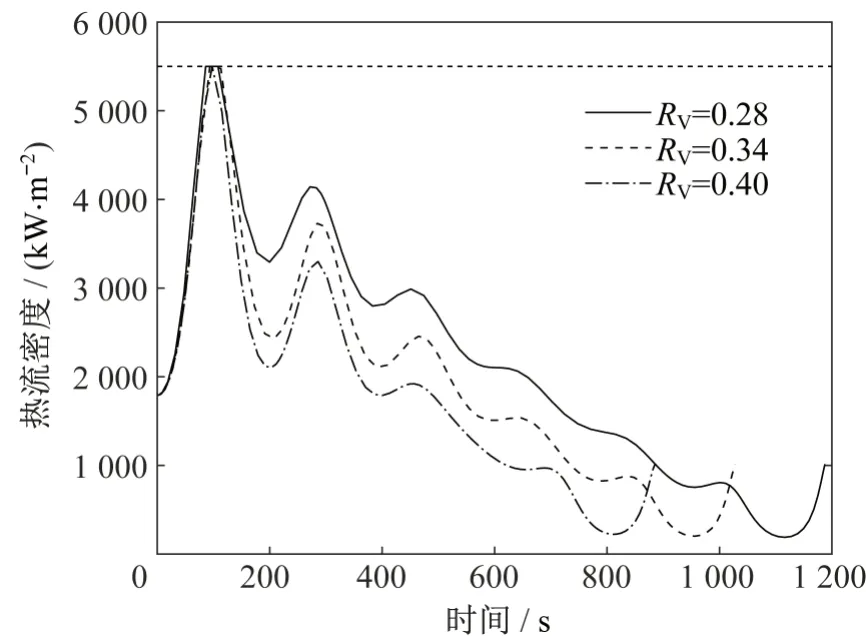
图8 热流密度与时间Fig.8 Heat flux versus time

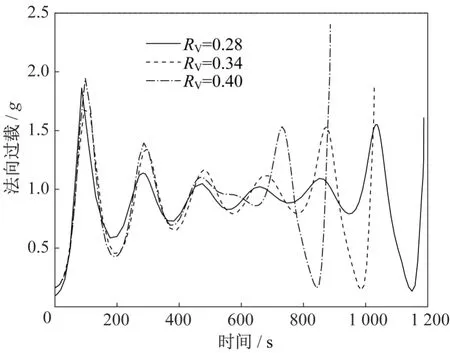
图9 法向过载与时间Fig.9 Normal overload versus time

图11 俯仰力矩系数与时间Fig.11 Pitching moment coefficient versus time

由图13可知，滑翔飞行器的最大航程与容积率之间存在指标冲突，即最大航程随容积率的增大而减小，且对于本文飞行器，最大航程与容积率呈现近似线性关系。对于不同容积率约束下的优化结果，容积率均达到约束下限值，因此容积率亦为飞行器最大航程的限制因素。此外，对于优化结果，随着容积率的增大，Hbu随之明显增大以满足容积率要求；Hbd均为下限值，即增大Hbd不利于提升最大射程；Lb均为上限值，即较大长细比有利于提升最大射程；nb均为较小值，表明飞行器的头部宽度较小；空气舵的外形尺寸由轨迹优化确定，即在满足配平能力约束下降低阻力，优化结果中，空气舵均具有较小的根梢比，且舵面前缘具有一定后掠角。质心位置系数k0分布在上限值附近，结合图12 可知，飞行器飞行过程中先处于临界稳定状态，而后处于静稳定状态，且采用较小的舵俯仰偏角即可实现配平。

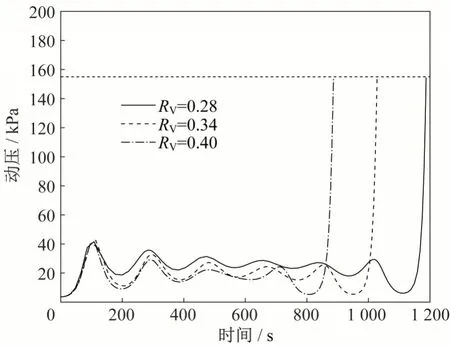
图10 动压与时间Fig.10 Dynamic pressure versus time

图12 配平俯仰舵偏角与时间Fig.12 Equilibrium pitching rudder angle versus time

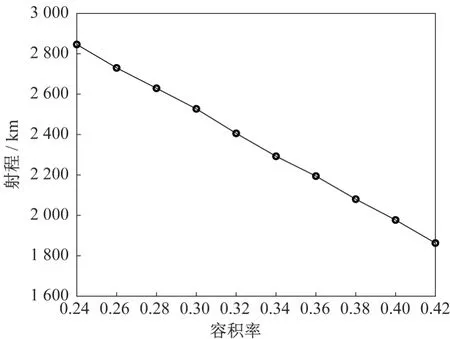
图13 射程与容积率Fig.13 Range versus volume efficiency

由表3 可知，经过MEGO 算法优化后，飞行器的最大航程相对基准方案的最大航程提升了近10%左右，当容积率约束边界为RVmin=0.40 和RVmin=0.42时，初始采样无法得到满足全部约束条件的基准方案，但采用MEGO算法即可获得最优可行解。根据表3 可以发现，MEGO 和EGO 算法得到的最优结果一致，且均满足全部约束要求，但MEGO 算法对学科分析模块的调用次数均少于EGO 算法对学科分析模块的调用次数，因此MEGO 算法的优化计算时间较EGO 算法的优化计算时间也有显著降低。由于EI 准则兼顾指标函数和代理模型的预测误差，经过数次加点后，最优解附近的EI 函数值可能较小，使得后续加点多处于样本点较为稀疏的区域，导致最优解附近的代理模型精度改善较慢，而MEGO 算法加入MP 点则能有效改善EGO算法局部收敛速度，验证了本文算法的有效性。