特殊化思想助力解题活动

郭红清

[摘 要]特殊化思想是重要的思维品质，特殊化能夠缩小探索的范围，或者给已知量增加更多的材料来降低难度，又或者强烈的隐喻激发了联想.

[关键词]特殊化思想;思维品质;解题

特殊化思想是从化归中抽出的具有实践指导价值的思想方法.一般问题和特殊问题并不等价，但解决特殊问题的思想方法对解决一般问题有较高价值.特殊化思想可用来进行解前预判、寻找思路、确定目标、解后验算等，是重要的思维品质.波利亚把找到辅助问题、追加条件等特殊化策略认为是解题的思路源泉，数学学习能力较强的学生更多的具备利用特殊化思想的行为自觉，解题更为迅速，更容易找到思路.本文以若干高考题为例，在实践层面上对特殊化思想的应用加以讨论.

一、构造特殊函数，迅速求出答案

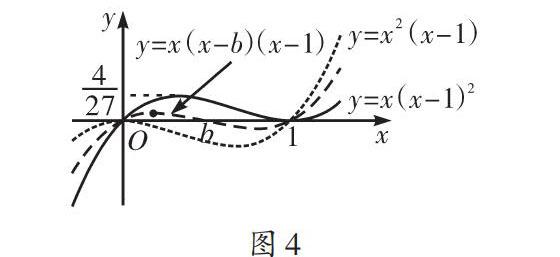
点评 ：首先[c=9]只是满足题意的一个答案，是否是唯一答案不能得证;其次未能揭示各参量的内部关系.考虑一般情况，二次函数图像顶点总可以平移至坐标原点，保持不等式[f（x）

二、构造特殊图形，化难为易

分析：确定三角形需要三个不相蕴含的条件，题目提供了两个;本题是个求值问题，意味着三角形未定但不影响结果;题中三组数量积同构，计算逻辑相通;点[E]位置在线段[AF]之间，答案大于-1小于4更为合理.

点评：本题设计较好，定式思维一般是选择基底或建坐标系，但是基底不容易选择恰当，直接建立坐标系也很难.挖掘隐含信息，追加特殊条件使原图化为特殊图形，建立坐标系计算简单，速度快.

三、举例特殊情况，先猜想后证明

点评：本题极大值的表示很难，稍有特殊思想的意识不难举出两个特殊情况，且特殊情况数据清晰，相应基本图形简洁，联系两个特殊情况的中间地带，图像非常直观，使得解题目标更明确，提示了解题方向和突破口.

波利亚在《数学的发现》的“思维的作用”部分中指出，所有的解题者都要猜，肤浅的猜和深思熟虑的猜却有所不同.特殊化思想被诟病的点就是让解决问题看上去有点像“猜”.特殊化的妙处在于特殊启示着一般，而且有机会去恢复一般.特殊化思想提出了与已知问题相关性强、接近度高的特殊问题，通过特殊问题能够缩小探索的范围，或者给已知量增加更多的材料来降低难度，又或者强烈的隐喻激发了联想.解题思维的作用并非玄妙的完全无法传递，比如特殊思想仍然是可以通过具体案例加以锻炼和培养的，只不过要求教师和学生多付出一点思考和试探的时间罢了，我们应当知道，知识是思维的载体，数学思想远远比数学知识更加重要.

[   参   考   文   献   ]

[1]  乔治·波利亚.数学的发现[M].北京：科学出版社，2015.

[2]  孟泰.高中数学阅读：微专题[M].南京：南京大学出版社，2019.

（责任编辑 陈 昕）