依托“问题导学”落实立德树人

陈茵

[摘 要]新课标强调数学教育要落实“学生发展为本，立德树人，提升素养”.落实立德树人，探索课堂育人的实施策略，已成为当务之急.

[关键词]问题导学;立德树人;曲边梯形

进入互联网时代，信息呈指数爆炸型增长，技术更新周期缩短，社会要求人们对新事物的自主学习能力更加高.面对国际市场的发展，社会要求人们加强合作共赢.为了培养符合社会需求的人才，高中教育要落实立德树人的根本任务，培养学生自主学习的能力，提倡终身学习.课堂教学要丰富学生的精神文化内涵，借助数学史、数学家故事等文化教育，落实德育教育.

教师已经意识到以知识传授为主的传统课堂教学不利于学生素养的提升，但是对“立德树人”融入课堂的方法没有明确.笔者以“问题导学”新授课教学模式五环节为框架，以“思维育人”“史料育人”“审美育人”“文化育人”“目标育人”五个维度，明确课堂育人的思路和方法.

一、教学策略

本节课采用“问题导学”新授课教学模式，利用教学的五个环节，将立德树人融入数学课堂.

新课引入环节，教师要解决“为什么学”的问题.数学史引入课堂，能让学生了解本节课的内容是如何发生、如何发展的，介绍学习新知的必然性，能使学生更全面地了解本课内容.在知识发展的过程中，古今中外涌现出了大量的有趣的数学故事，数学家们不惧困难、锲而不舍、为科学献身的精神值得学习.新课引入数学史，使得引入与课程内容更具关联性.

概念形成环节，教师要解决“如何学”的问题. 概念形成过程中，旧知与新知的顺应和同化，需要教师设计有梯度的探究问题，引导学生建构新的认知结构.教师还需要引导概念形成过程中涉及的数学思想和方法，培养学生科学的探究精神.

概念深化环节，教师要挖掘新知的内涵与外延.从学生最近发展区出发，通过设计有梯度的探究问题，为学生搭“脚手架”，帮助学生理解概念.通过挖掘知识的内涵和外延，培养学生的数学核心素养.

应用探索环节，教师要培养学生发现问题、提出问题、分析问题和解决问题的能力，鼓励学生学以致用、举一反三.

总结归纳环节，教师要帮助学生梳理课堂知识，建构认知结构，培养学生总结归纳、概括的能力.

课堂上还可以借助现代信息技术、数学软件等多媒体手段，降低抽象知识的理解难度，培养学生合理运用现代技术的能力.

二、教学案例

【内容分析】《曲边梯形的面积》是人教A版选修2-2第一章第六小节的内容，是定积分概念教学的第一部分内容，为定积分概念的提出奠定了基础.本节课利用具体的曲边梯形的面积求解过程，体现了“以直代曲”“无限逼近”的极限思想.

【教学目标】

“四基”目标：

1.通过特殊实例，探究求曲边梯形面积的四个步骤，了解定积分的几何意义;

2.通过“以直代曲”“无限逼近”的思想方法，为学生理解定积分的概念奠定基础，体会极限的思想;

3.通过解决求解曲边梯形面积，培养学生发现问题、提出问题、分析问题和解决问题的能力.

“素养”目标：

1.从曲边梯形面积求解过程中的分割、取极限，培养学生的数学抽象素养;

2.对分割后的矩形面积求和，培养学生的数学运算素养.

【学情分析】在此之前，学生学习了导数的定义，初步体会到极限的思想，具备了求解积分的知识.但是，学生对极限的理解比较浅，无法体会“无限趋近”.

重点：掌握曲边梯形面积求解“四步骤”，体会“以直代曲”“逼近”的思想.

难点：极限思想的形成过程，求和符号的理解.

【教学过程】

（一）新课引入

课前预习任务：

观看微课视频《刘徽—割圆术》（https：//www.bilibili.com/video/BV1df4y1D7zM？t=210）并查阅相关资料，尝试归纳出割圆术计算圆的面积的步骤，体会其中的数学思想.

设计意图：微课视频动态地展示了正多边形分割圆的过程，便于学生观察分割近似的过程，利于理解“以直代曲”“逼近”的数学思想.刘徽的割圆术中提出的“割之弥细，失之弥少”是中国古代数学史上经典的极限思想的体现，与本节课曲边梯形面积的求解具有关联性.刘徽利用割圆术得到圆周率精确到小数点后四位，让学生能体会到数学家锲而不舍的钻研精神.

问题一：类比计算圆的面积的计算方法，如何求椭圆的面积？如何计算曲边梯形的面积？

设计意图：椭圆是学生熟悉的曲边图形，与圆的性质的研究思路相似，从中引出本节课的课题：如何求曲边梯形的面积.

（二）概念形成

（2）近似代替.每个区间的曲边梯形面积可用对应的矩形面积代替.

（3）求和.曲边梯形面积S的近似值.

设计意图：与圆面积的求法一样，通过计算直边图形面积去逼近曲边图形的面积.从简单的图形出发，经历分割、近似代替、求和、取极限的过程，便于学生归纳求曲边梯形面积的四个步骤，让学生体会从特殊到一般、从具体到抽象的思维方式.

借助GeoGebra软件动态展示分割逼近的过程.

第一步，指令栏中输入[y=x2];

第二步，插入滑动条，设置最小值2，最大值100;

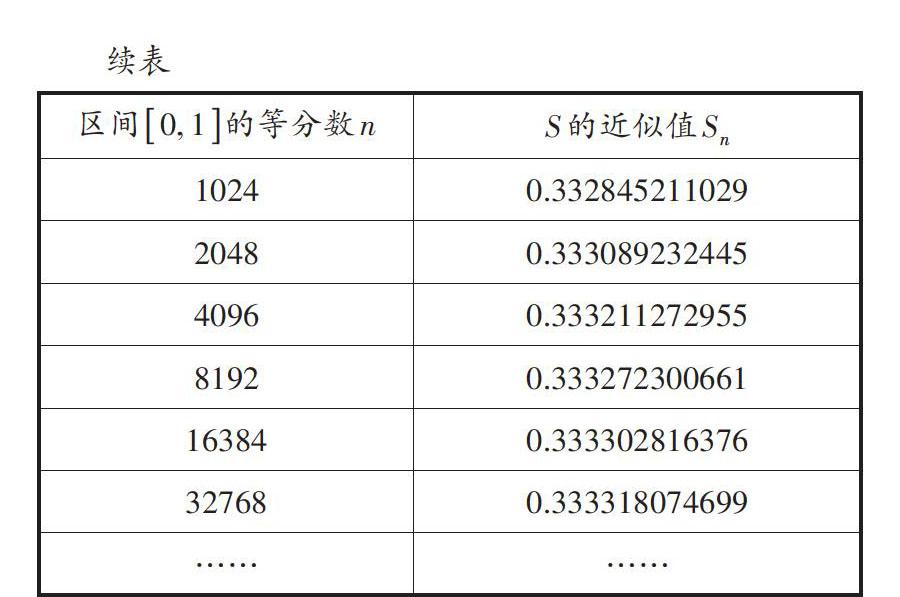
第三步，指令栏中输入：下和[（f， 0， 1， n）]，移动滑动条，观察图像.

设计意图：从图像的分割和图表的数据两方面，帮助学生理解极限思想，体现数形结合思想.

（三）概念深化

学生以小组为单位，借助GeoGebra软件，探究以下两个问题.

问题四：分割是否需要等距？

问题五：在“近似代替”中，函数在区间[i-1n，in]上的函数值能否用右端點函数值[fin]代替？任取[ξi∈i-1n，in]处的函数值[f（ξi）]作为近似值，结果会发生变化吗？

设计意图：强化学生对曲边梯形求解的四个步骤及极限思想的理解.教师在课堂中充分利用多媒体工具辅助教学，培养学生的动手探究能力，让学生学会用辩证的观点看待问题的方法，学会用数学的思维思考世界，用数学的眼光看待世界，用数学的语言描绘世界.

（四）应用探索

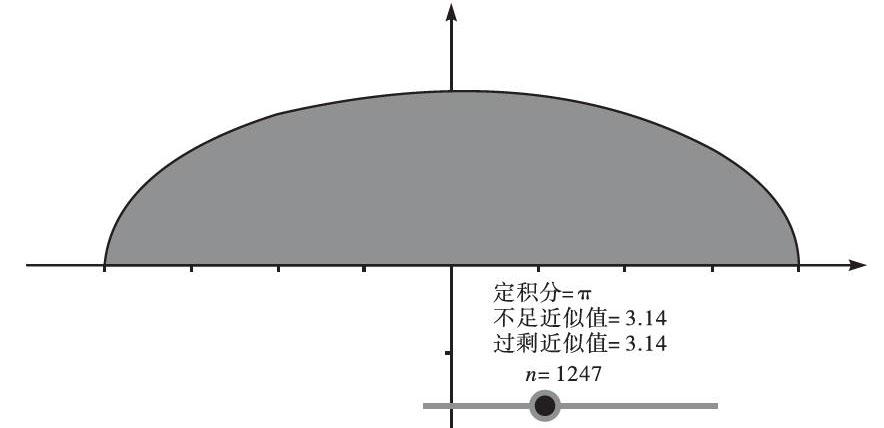
[例2]根据以上求曲边梯形面积的四个步骤：分割—近似代替—求和—取极限，借助GeoGebra软件，解决问题一：椭圆[x24+y2=1]的面积是多少？

将椭圆沿着[x]轴进行分割，上半部分再进行等距分割.取区间右端点函数数值近似代替区间的函数值.借助GeoGebra软件对小矩形的面积进行求和.

设计意图：借助GeoGebra软件，利用求曲边梯形面积的四个步骤，求解椭圆的面积.有计算机软件的加入，将特殊函数围成的曲边梯形面积推广到任意曲边梯形，培养学生将数学思想方法应用到解决实际问题中，培养学生的数学建模素养.

（五）总结归纳

问题：请归纳求曲边梯形的四个步骤.回忆所学的知识，还有哪些用到了极限思想？利用曲边梯形面积的方法，你还可以解决哪些实际问题？

设计意图：让学生自主建构知识体系，学以致用，拉近数学与生活的距离.

三、教学反思

课堂是落实立德树人的主要阵地.明确新授课的五个教学环节，每个环节有明确的育人目标，能更好地将育人落到实处.

数学史能帮助学生了解知识的“前世今生”.教师通过讲故事、播放微课视频等形式将数学史引进课堂，丰富学生的情感生活，达到史料育人、文化育人的目的.“割圆术”的基本步骤与求曲边梯形的方法类似，从学生已有的知识出发，让课堂引入更具关联性.

现代信息技术能拉近数学与生活的联系，借助GeoGebra软件将“以直代曲”“无限逼近”达到可视化的效果，降低学生理解的难度.信息技术与课堂教学融合，能培养学生的创新精神和实践能力.

小组合作学习能培养学生的合作精神、探究精神.课堂中设计探究问题，有意识地组织学生合作，让学生学会表达、学会探究，让课堂成为培养合作型人才的主要阵地.

（责任编辑 黄桂坚）