讲好数学育人故事

作者简介

陈六一，南京师范大学苏州实验学校教科室主任，高级教师，全国科研先进工作者，江苏省教育科学成果奖一等奖获得者，苏州市数学学科带头人，苏州市优秀教育工作者，《教师博览》签约作者，多家教育期刊外审专家，发表教育教学文章近200篇，其中20多篇被人大复印报刊资料全文转载或索引。

摘 要： 数学知识本是教师进行教学的根本，当下却出现了拥有高学历的老师、会解题的学生不甚理解数学的现象。为了使学生的生物脑成为智力脑，就需要数学教师不仅讲推理，更讲道理;不仅讲思考，更讲思想。这样通过学科知识的视角讲数学故事，才有可能让数学育人在课堂真正发生。

关键词：深刻理解;数学育人;智力脑;数学素养

王子兴教授指出，数学学科知识是小学数学教师进行教学的根本，包含三个层次：（1）覆盖数学知识体系的数学结构、数学思想与数学方法;（2）现代数学的基础知识、数学的渊源与实质;（3）应用数学方面的知识。全美教师理事会在其报告《数学教师标准》中说，教师在数学学科知识方面要理解数学概念、过程及其关系，多种方式表述数学，能以不同形式进行数学交流，了解数学本质的变化带来的教学方式的变化，不同文化、学科对数学发展的影响，以及数学在生活中的作用。概括而言，数学学科知识包括数学内容的知识和关于数学的知识。数学内容的知识是指对数学概念、过程及其关系的理解，数学的知识是指数学从哪里来、发生了怎样的改变。

反观当下一线小学数学教师，尽管他们对小学数学教材乃至各种辅导材料中的习题，都能不费力地解决，但笔者通过课堂观察却发现，他们对数学学科知识的理解普遍不够深刻（教师会解题不等于理解数学）;加之目前的校本培训、业务进修、专题教研，主办者一般都会围绕教育理念、教学艺术、课程建设等方面来开展，却常常忽视对学科知识的指导（大家都认为小学数学知识很简单）。而恰恰是由于教师对数学学科本身的理解存在欠缺，课堂中的数学学习充斥着形式化的、无意义的生物脑的训练，使学生能按套路做对题目却不懂数学。为此，张奠宙教授生前曾不断警示：“小学数学并不简单，甚至具有很高的学术含量。小学里有许多内容需要高屋建瓴地从数学本质的揭示进行梳理，仅就一些教育理念进行教学设计是走不远的。”确实，我们小学数学教师，虽然冠名以“小”，但任务不小，唯有不断追问“我懂数学吗？”才有可能讲好数学故事，让数学育人在课堂发生，让学生习得带得走的数学素养。

一、不仅讲推理，更讲道理

“是什么”即推理，“为什么”即道理。小学数学教师往往对“是什么”都有着清晰的认识，但对于数学为什么是这个样子，由于其和指导学生做对题目关系不大，加之教师自己一般不做这些追问，因此也就不能从本质上理解数学，不能从文化、思维游戏等维度发现数学的魅力，从而传递给学生的数学也就变成了“冰冷的名词”。例如，教学“因数和倍数”时，我们都知道当非0自然数a、b、c存在a×b=c时，a和b叫作c的因数，或者说c是a的倍数，也是b的倍数。并由此解释什么是质数、合数，即只有1和它本身两个因数的自然数称为质数;除了1和它本身外，还有其他因数的自然数称为合数。然而，为什么要把0排除在外呢？学习因数、倍数、质数、合数是为了什么？记得在一次公开课上，学生提出了这些问题，教师只是解释不考虑0是规定，它们属于纯数学问题。没有触动数学脉络的理答，注定不会吸引学生爱上数学，投身数学研究。那么怎样才算对因数、倍数的深刻理解呢？

在教学苏教版数学教材五年级下册“因数、倍数”时，笔者先出示一个数：2520。再讲述：“古代埃及的数学成就非凡，考古学家发现，在埃及金字塔的一块墓碑上，竟然刻着2520。你知道2520的意义吗？”学生做着各种猜想，然后又自我否定。数学好奇心强烈地驱使着学生一定要弄个明白。原来古人觉得数能解释世界，比如毕达哥拉斯学派曾提出“万物皆数”的学说，那么数必然有最基本的元素，就像物理世界的粒子，就像建筑物需要的砖块，可是在寻找最基本元素的过程中，如果只用1做单位来数数，会导致自然数只有1这一个基本元素，如2=1+1，3=2+1=1+1+1，4=3+1=2+1+1=1+1+1+1……数学就显得无趣了。于是接下来教师引导学生重新数自然数，并将数与形结合，学生在数数中感悟到1、2、3、5……这些自然数在直线上只有左右两个方向，是一维的;而4、6、8、9、2520……这些自然数不仅有左右方向，还有上下方向，是二维的，因此也叫矩形数。

在古代，0还未视作自然数，所以解决质数问题时，0没有纳入数论的范畴。尽管后来大家约定0为自然数，而数论依然把0排除在外，我们可引导学生了解： 0是一个点，在数轴上既无左右方向，更没有上下方向，是0维度，这便成了0不是数论研究对象的缘由。进而启发学生讨论为什么规定1既不是质数，也不是合数。其实在哥德巴赫眼里，1是质数，正如前文所述，因为1和2、3、5等自然数一样，都是一维的;后来人们用因数的个数来解释质数、合数，这样非0自然数先被分成两类，即只有1个因数的数和不止1个因数的数，当研究的角度只关注不止1个因数的自然数时，1就成了单独的集合。不止1个因数的自然数又可分成两类，即只有两个因数的数（质数）和多于两个因数的数（合数）。

学习进行到此，学生可以智慧地解决课堂开始的問题了。原来2520是1、2、3到10这十个连续自然数的倍数，而且是它们的最小公倍数，所以古代埃及人自豪地记录了这一发现。

可见，“是什么”让数学演变成了静态的观念，“为什么”则启示着数学是动态的、不断发展着的。在推理中叩问道理，也就是追寻静态背后的发展趋势，而这正是形成学生人生观、世界观的一种可能路径。

再如教学苏教版数学教材四年级下册“三位数乘法”时，不少教师过度关注乘的程序。展开来说，教师强调从低位算起，用哪个数字去乘，就写在哪一位的下面，然后重复练习求得技能自动化，而漠视乘的“为什么”。

其实，对于任意两个自然数，乘法运算法则分为三个部分：（1）两个一位数相乘，（2）任意一个数与一个一位数相乘，（3）任意两个数相乘。以145×326为例来理解，乘法法则的第一部分：先用145的每一个数字都乘6，6×5=30，在个位上写0，在十位上进3;6×4=24，在十位上写4，加上个位上进的3，十位上最终写7，在百位上进2;6×1=6，在百位上写6，加上十位上进的2，百位上最终写8。将同样的法则用于145×2和145×3，可以分别得到结果290与435。将145×6、145×2和145×3的积放在一起，也就是把870、290、435按如图1方式叠放。

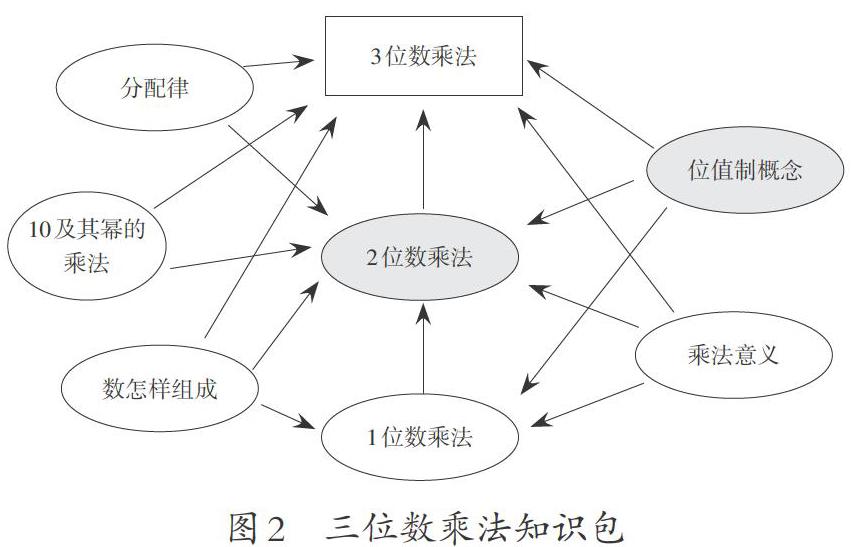
基于图1，实现了乘法法则第三部分：任意两个数相乘。这样无须去识记所谓的程序，学生可以根据自己的习惯、数感，创造属于自己的竖式;只是无论从哪里算起，终将变成两个一位数的乘法;结果写在其下方理由是算145×2，实际指向145×20，所以记录的时候要出现移位。一旦学生掌握了图1的方法，由此可以得到启示：乘多位数，既可以从低位算起，也可以从高位算起，甚至无论从哪一位算起都行。原来，计算就是遵从某种规则的游戏，于是不同水平层次的学生都有了算的念头，并在表达算的过程中，实现了马立平教授期待的“知识包”，即三位数乘法依赖于数的组成、乘法意义和一位数乘法、两位数乘法，利用了位值制概念，同时又为未来学习乘法分配律提供思维经验。

教师仅有程序性的“是什么”，其数学理解是碎片式的。而将知识点以联系的视角分析，形成“知识包”，就能举一反三，让数学学习在迁移中发生，让数学在“为什么”的根基上不断扩张。

二、不仅讲思考，更讲思想

越来越多的教师重视数学思考，让学生在思考中感受智力挑战带来的乐趣。但是，只有数学思考，还不能让学生感受到数学的美、源自数学的深刻。例如，教学苏教版数学教材五年级下册“分数的基本性质”时，教师往往会出示一些变式题促进学生思考，求得对“分子、分母同时乘或除同一个数”的真正理解，比如：（1）[416=2（    ）=（    ）48，]（2）[416=4+416+（    ），]（3）[416=4a（    ） （a≠0），]（4）[nm=][3nm+（    ）。]同时，教师也会引发学生对“商不变的性质”“小数的性质”进行关联，求得知识间的融会贯通。

但这些还不够，教师要往前再走一步，要通过“分数的基本性质”，让学生领悟等价类思想。等价类数学思想，指的是同一类对象具有某种等价性，也就是用一个相等的准则，把彼此相等的对象归为一类，同一类对象，本质一样，只是表征形式不一。以此审视分数：一个分数的值有无限种表达形式，例如[12]和[24，36，48，510]……相等。学生以往学习自然数时，1只能等于1，2只能等于2，未曾发生过1、2可以写成其他形式。分数的等价，扩充了学生的视野，让学生习得尽管不同的数、不同的形，有着各自的意义，但是通过比较大小，可以看透不同中的相同。这样，相等的角是一种等价类，以等价类来学习角，学生领悟角的边，可以是线段，可以是射线，角相等是指角区域的大小相等，自然与边的长短無关，于是各个学段学习角都是等价的。换句话说，第一学段认为角有一个顶点和两条边，第二学段教材对角的解释是从一个顶点引出的两条射线，欧氏几何定义角是两条直线的位置关系，以及旋转定义：角是射线旋转而形成的图形。这些定义都是等价的，只是限于学生的年龄特点，用了不同的说明方式。这样，解相等的方程也是一种等价类，于是不同的数量关系式、不同的未知数，在直角坐标系中都有了相同的图像。

例如，在教学苏教版数学教材五年级上册“小数的意义”时，除了思考小数与分数的关系，掌握一位小数是十分之几、两位小数是百分之几……教师还要懂得小数反映着量化的数学思想。整数、小数都以1为度量单位，往大的方向计数，是10倍的方式累计;往小的方向计数，是10倍的方式均分（分数是任意倍数方式的均分）。量化思想启示着学生：第一，数本身的扩张具有一致性，不论整数还是小数，其计数原理相同。为什么百分之几是两位小数，就是因为第一次以10倍的方式均分，数出的几份记在个位的右边第一位;再一次需要以10倍的方式均分，数出的几份记在十分位的右边第一位，也就是均分100份，数出的份数用两个数字来记录，依次记在个位的右边。第二，小数代表着先进文明，古人用不断创造新度量单位的方式表示精确程度，如里、引、丈、尺、寸、分、厘、毫、丝等，但这给学生的记忆带来了麻烦，小数只需要一种单位，就能表示这一切。显然，小数是大脑冒险的产物，是逻辑的力量;同时，大脑的冒险，让度量工具得以革新，如纳米技术、芯片技术。第三，量化是解释世界的一种方式，万物一旦定下了“1”，便能赋予数;有了数，便可以加减乘除。于是，数学公式、数学运算就让不容易描述的、难以表达的现象可以讲道理，让只能靠想象而无法言明的道理得以可视化。所以教师不仅要教数学思考，更要教数学思想。

当然，正如张奠宙教授所言：“小学数学要做到浅而不错、分而不碎不是一件容易的事情。”这需要一线教师对数学学科知识有深刻的理解。对数学有深刻的理解，教师就能将数学所涵盖的各种成分迅速转换，就能知晓学生以后会学习到哪些知识，在课堂上予以适当铺垫，就能用更高的观点统领数学，平衡数学的逻辑与教学的逻辑。

总之，教师对数学有深刻的理解，才能实现上通数学，下达课堂;才能以数学的本真，涵养现代公民应具备的数学素养。

（作者单位：南京师范大学苏州实验学校）

参考文献

[1]王子兴.数学教育学导论[M].桂林：广西师范大学出版社，1996.

[2]郜舒竹.小学数学教学基础[M].北京：中国人民大学出版社，2015.

[3]张奠宙，巩子坤，等.小学数学教材中的大道理[M].上海：上海教育出版社，2018.

[4]马立平.小学数学的掌握和教学[M].上海：华东师范大学出版社，2011.