基于最大丰满系数的凸轮传动机构仿真优化

2021-09-15李参军曾文浩徐大伟杨永泰

机械设计与制造工程 2021年8期

李参军，曾文浩，徐大伟，杨永泰

(1.中科院海西研究院泉州装备制造研究所，福建泉州 362216) (2.中北大学机电工程学院，山西太原 030051)

凸轮机构是机械传动系统中的一种基本机构，因其具有结构简单、紧凑，传动效率高等优点而被广泛使用。在凸轮传动机构中，凸轮轮廓曲线是一个重要的设计变量[1]，一般来说，只要设计出合理的凸轮轮廓曲线，就可以使从动件的位移、速度、加速度按预定运动规律变化[2-3]。不合理的凸轮轮廓曲线会导致凸轮与从动件发生碰撞，特别是在高速传动过程中，往复运动带来的惯性力会引起强烈的振动与冲击[4]，严重情况下甚至会出现凸轮破损、断裂的现象。因此，合理设计凸轮轮廓是保证传动系统稳定、可靠运行的基础。

金属排咪机又称方牙机，是一种生产服装拉链的重要设备，其工作原理是通过凸轮传动完成Y型铜材切断、牙点冲压成型、挤压至布带上等工序，制成整条拉链。我国的金属排咪机大多是参照国外机器研制而成，但在生产效率与产品质量上与国外差距很大，全球高端奢侈品级别的拉链市场几乎被日本YKK和瑞士RIRI垄断[5]。排咪机的核心机构是凸轮打点机构，其具有转速高、结构紧凑、惯性力大等特点。但是，当该凸轮机构高速运转时，由于从动件的惯性力剧增以及滚子与凸轮间的相互碰撞，会引发机构的强烈振动。另外，冲针过大的速度突变不仅会减少冲针的使用寿命，还会带来机身的冲击振动，加剧关联机构的磨损。因此，如何减少机构的振动和延长凸轮的寿命，是改进排咪机的研究重点。ADAMS软件[6]是使用范围最广的动力学仿真软件，很多学者利用ADMAS对凸轮传动系统进行了动力学仿真分析，如万朝燕等[7]基于ADAMS建立了高速凸轮机构的弹性动力学模型，获取从动件运动规律曲线，重点分析了不同推杆刚度下高速凸轮机构的动力学特性；刘小月等[8]利用数值分析方法对高速凸轮机构进行了动态研究，证明了数值分析方法可以很好地应用在高速凸轮机构动态分析中；金国光等[9]采用有限元法建立刚柔耦合凸轮系统动力学模型,通过截取不同阶次的动力学模型来考察高速凸轮机构的固有频率与振型，重点分析了模态截取阶数对计算精度和速度的影响；玄冠涛等[10]采用改进人工鱼群多目标动力学优化算法对高速凸轮NURBS廓线进行了优化，并利用非均匀有理B样条(NURBS)重构了凸轮轮廓线，最后通过建立高速凸轮单自由度弹性动力学模型，验证了多目标优化算法的正确性。近年来，虽然相关研究领域的很多学者都基于数值分析方法对凸轮传动机构中的凸轮轮廓进行了设计与优化，但往往都是在不考虑凸轮间的接触摩擦力的情况下进行的，而一旦引入接触摩擦力，原有的凸轮轮廓设计会导致凸轮间的碰撞振动，传动系统的性能大为降低[11]。

本文以排咪机中的凸轮打点机构为例，在ADAMS环境下考虑凸轮与滚子间的接触碰撞，对凸轮打点机构进行动态设计与仿真研究，发现凸轮轮廓曲线不合理是引起冲针加速度波动较大的主要原因，然后基于最大丰满系数理论对凸轮轮廓进行了优化，最后利用优化后的凸轮轮廓曲线进行了凸轮重构和相应的凸轮传动动力学仿真。仿真结果表明：优化后的凸轮在传动过程中，速度曲线更加光滑，加速度曲线更加平缓，说明凸轮与滚子间的碰撞明显减少，冲针运行更平稳，机构动态性能得到了明显改善。

1 模型建立

1.1 工作原理

凸轮打点机构是排咪机的核心部件，其结构简图如图1所示。凸轮绕O点转动时，通过与其接触的滚子B带动摆臂BAC绕A点摆动，从而使冲针CD做间断式打点往复运动，冲针打点的幅值和周期分别为4.13 mm、0.043 s。为使滚子和冲针能够在高速运动情况下及时回复，还需在滚子及冲针上添加弹簧以提供必要的预紧力。

图1 凸轮打点机构简图

1.2 导入模型

将在CREO中建立的三维模型保存为Parasolid(x.t)格式的文件，然后导入到ADAMS软件中。导入ADAMS中的凸轮打点机构模型如图2所示。

模型导入到ADAMS软件后还需要对凸轮打点机构各个构件进行材料的设置和构件之间的约束设置，本文打点机构中构件的材料全部选用合金钢，令大地为构件0，构件间约束的设置见表1。

表1 冲压打点机构构件约束表

在图2中4和7处添加弹簧，其刚度均为500 N/mm，预载力均为1 500 N。对凸轮轴添加驱动，驱动速度为1 400 r/min。

1—凸轮轴；2—滚子轴；3—滚子；4—弹簧；5—摆臂；6—柱销；7—弹簧；8—冲针；9—滑道；10—凸轮

2 仿真分析

2.1 不考虑接触碰撞与摩擦的仿真分析

在凸轮与滚子间加入凸轮副，即不考虑滚子与凸轮的接触碰撞。然后在冲针尖端建立MARKER点，以该MARKER点坐标系为基准，对冲针在竖直方向上的位移随时间的变化进行仿真，在仿真结果中截取两个周期的冲针s-t曲线，如图3所示。

图3 冲针s-t曲线图

由图3可知，冲针先从打点最底端开始回程运动，然后静止、再打点往复运动两个周期，冲针的运动幅值约为4.13 mm，周期约为0.043 s，以上运动规律与实际工作情况一致，说明了模型建立的正确性。

2.2 考虑接触碰撞与摩擦的仿真分析

实际运动过程中，凸轮与滚子间总是存在接触碰撞，ADAMS软件里有两种定义碰撞力的方法：一种是补偿法(restitution)；另一种是冲击函数法(impact)。补偿法要求软件用户给出惩罚系数(penalty)和补偿系数(restitution)。两个构件之间相互接触运动的重合部分刚度取决于惩罚系数，两个构件相互接触运动的能量损失取决于补偿系数。由于惩罚系数与补偿系数难以确定，因此多用冲击函数法来计算碰撞力[12]。

Impact函数的表达式为：

(1)

式中：k为刚度系数；e为非线性指数；cmax为阻尼系数；step(·)为阶跃函数；q0为碰撞开始时两个物体的距离；q1为碰撞过程中两个物体的实际距离；t为时间；d为切入深度。

Impact模型里面的接触力由两部分组成：k(q0-q1)e是类似于非线性弹簧的弹性分量，cmax·(dq1/dt)·step(q1,q0-d,1,q0,0)是阻尼分量。

凸轮与滚子之间的接触可以看作是两个圆柱体的碰撞，两圆柱体撞击时法向接触力F和变形x的关系为：

F=Kx2/3

(2)

式中：K为接触刚度。阻尼分量可依据Hertz弹性碰撞理论计算，碰撞过程中的变化由弹簧控制。

接触刚度计算公式如下：

(3)

其中：

(4)

(5)

式中：R1，R2分别为凸轮及与其接触的滚子在接触点的当量半径；μ1，μ2分别为凸轮材料和滚子材料的泊松比；E1，E2分别为凸轮材料和滚子材料的杨氏模量。

依据以上相关碰撞的理论，在凸轮与滚子间添加接触，接触类型为Solid to Solid。凸轮和滚子材料均为合金钢，Stiffness值定为1.0E+05 N/mm，Force Exponent取1.5；阻尼贡献值比较小，可取阻尼系数为50 N·s/m；由于滚子与凸轮间的接触刚度比传动轴的扭转刚度大得多，因此接触处的弹性变形比较小，可以忽略，穿透深度取0.1 mm。

为了更贴近实际情况，进行动力学分析时往往需要考虑摩擦的存在，因此在凸轮与滚子处添加摩擦力，摩擦力采用软件的默认值。对凸轮打点机构进行仿真，得到冲针在竖直方向上的位移、速度、加速度曲线，选取对应的两个周期分别与未考虑接触情况下的冲针动态性能曲线进行对比，如图4所示。

图4 冲针动态性能曲线对比图

由图4可以看出，加入接触碰撞与摩擦力后的冲针位移曲线与不考虑接触情况下的曲线基本重合，速度有所波动，加速度波动十分明显。加速度的突变会带来柔性冲击力，在低速时这种冲击力还不明显，但在高速时该冲击力会变得很大，成为产生过大噪声和振动的主要原因。为减少机构振动，使冲针速度稳定，加速度更小，有必要进一步优化凸轮轮廓曲线。

3 凸轮轮廓优化设计

本文中摆臂、冲针等构件固有频率远远大于所施加的激励频率，因而可以忽略弹性体变形的影响。模型中的凸轮是基于反转法由机构行程反推设计出的，但是这种设计方法设计的凸轮从动件加速度曲线往往存在突变，从而导致机构的冲击大、振动严重、磨损加剧。

基于最大丰满系数理论优化设计凸轮常应用于内燃机等的配气机构，主要是由于其可保证凸轮机构冲击小、振动小，使从动件具有较小的加速度以及较高的进、排气效率[13-14]。本文所研究的凸轮打点机构中冲针的运动状况类似于配气机构中的气门，因此可采用最大丰满系数理论优化凸轮轮廓，从而保证机构在较小的冲击、振动情况下，冲针具有较高的打点和回程效率。

凸轮打点机构的凸轮轮廓常用高次多项式曲线表示，其高次多项式表达式为：

hφ=c0+cpθp+cqθq+crθr+csθs+…

(6)

式中：hφ为凸轮升程；c0,cp,cq,cr,cs为待定系数；p,q,r,s为幂指数，p=2，q=2n,r=2n+2m,s=2n+4m,m+n=2，m和n为约束函数。凸轮上升段θ=(φ0-φ)/φ0，凸轮下降段θ=(φ-φ0)/φ0，其中φ为凸轮转角，φ0为凸轮半包角。

凸轮工作段的升程速度vφ、加速度aφ、凸轮轮廓线坐标(xφ，yφ)和轮廓坐标曲率半径Rφ为：

(7)

(8)

(9)

(10)

(11)

式中：w为凸轮转速；R0为凸轮基圆半径。

3.1 目标函数与设计变量

评价凸轮机构性能的指标是凸轮的丰满系数ζ，ζ值越大，说明凸轮机构的性能越好。丰满系数表达式为：

(12)

式中：

c0=hmax;

其中，hmax和v0的值可由机构初始条件确定。于是目标函数为：

(13)

式中各项均可以用m和n来表示，因此有：

3.2 约束函数

对机构中从动件滚子的最大正加速度amax、负加速度amin和凸轮最小轮廓曲率半径Rmin进行限制，即amax≤[amax],amin≥[amin],Rmin≥[Rmin],其中[amax]、[amin]、[Rmin]分别为滚子最大正加速度、最大负加速度和最小曲率半径限定值。设计变量取值范围为3≤n≤20,1≤m≤20。约束函数Ki(X)如下：

(14)

3.3 凸轮模型参数及优化结果

凸轮原有参数如下：轮廓圆弧最小曲率半径R=20 mm，凸轮基圆半径R0=23 mm，最大升程h=4 mm，轮廓半包角φ0=70°，凸轮转速ω=8 400 (°)/s。原机构滚子落座的最大速度为0.89 m/s，滚子落座最大正加速度为amax=1 653.8 m/s2，滚子落座最大负加速度为amin=-1 298.3 m/s2。基于以上参数，设计一个五次多项式凸轮。

式(14)是一个不等式约束二变量非线性规划问题，本文采用序列规划法对目标函数进行优化，编制了相应的MATLAB程序，得到优化参数，在求出n和m最优解后即可求出凸轮曲线方程，进而按凸轮相关参数拟合凸轮轮廓曲线[15]。

优化结果如下：n=4.927，m=5.402，ζ=0.664。

4 动态特性改善结果

对优化后的凸轮轮廓线在CREO中建模并以Parasolid(x.t)的格式导入ADAMS中，导入时注意选择凸轮轮廓线对应的实体，添加对应的边界条件。在其他设置不变的情况下，选取对应的两个周期对比分析优化前后对冲针运动规律的影响，如图5所示。

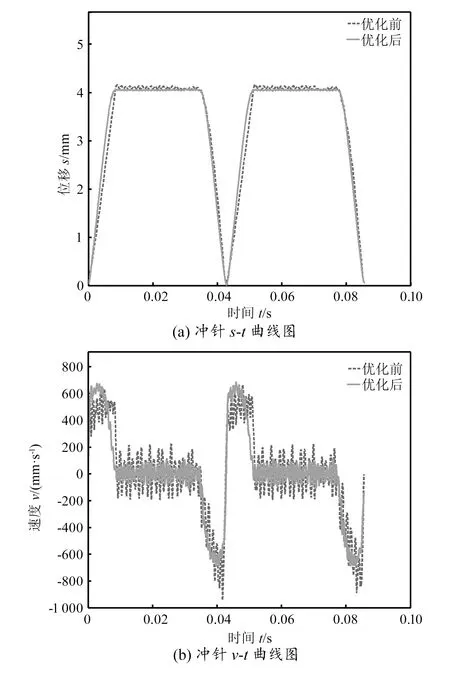
图5 优化前后冲针动态性能曲线对比图

由图5可知，凸轮优化前后冲针的周期和幅值几乎不变，说明了优化后的结构没有改变从动件的工序要求。优化后的速度-时间曲线相比优化前更加圆滑稳定，优化后的加速度-时间曲线相比优化前波动幅值更小，这些都说明了优化后凸轮与滚子间的冲击大为减小。从动件的最大速度反映其最大冲量大小，从动件的最大加速度反映其惯性力大小[16]。从图中可明显看出，优化后结构中冲针的速度、加速度均小于优化之前，因而可以从理论上说明执行末端的动态稳定性好。

对于高速运动的机器，最容易产生冲击振动的地方无非是发生在具有相对运动关系且作用力不断变化的位置。在摆臂与冲针的衔接处，对优化前后此处的受力情况进行仿真对比分析，结果如图6所示。由图可以发现，通过对凸轮的优化，此处的接触力幅值大为减小，接触力的幅值减小也说明了此处的冲击振动减小。