盐碱土入渗下修正Green-Ampt模型参数确定与验证

2021-09-15陈俊英何旭佳杨亚龙白旭乾谢林林

农业工程学报 2021年12期

陈俊英，何旭佳，杨亚龙，白旭乾，李毅，谢林林

（1. 西北农林科技大学旱区农业水土工程教育部重点实验室，杨凌 712100；2. 西北农林科技大学水利与建筑工程学院，杨凌712100；3. 西北农林科技大学理学院，杨凌 712100）

0 引言

盐碱土是碱土与盐土的总称，在中国总面积超过0.33亿hm2，占灌溉面积的15%[1]。土壤中的盐分离子影响作物水分吸收，对作物生长造成危害[2]。盐碱土的改良利用与盐碱土的入渗规律研究息息相关，掌握盐碱土的入渗特性，建立盐碱土的入渗模型尤为重要。

Green-Ampt模型是1911年Green与Ampt根据土壤毛管理论提出的土壤入渗模型[3]，计算精度较高，因而得到广泛应用。随着研究深入，Green-Ampt模型不断被修正应用于初始含水率不均的土层入渗[4]、层状土[5-6]以及浑水入渗[7]、降雨入渗[8]等研究领域，证明了该模型拥有广泛的适用性。赵伟霞等[9]建立了适用于恒定水头井积水入渗的Green-Ampt模型，联立入渗率与累计入渗量的表达式，反求土壤导水率与湿润锋面基质吸力，并发现恒定水头井入渗下土壤湿润体呈椭球体。Ma等[10]对大型分层土壤土柱进行扩大试验，采用了Bouwer方法对Green-Ampt模型进行修正，修正模型模拟效果良好。针对Green-Ampt模型的修正集中在土壤导水率与湿润锋面基质吸力两个参数的变换求解，问题难度较高。迄今已有大量使用该入渗模型拟合盐碱土入渗过程的研究，周蓓蓓等[11]施加枯草芽孢杆菌改良盐碱土，并分别采用Philip和Green-Amp模型拟合入渗数据，结果显示Green-Ampt模型的拟合数据误差小于Philip模型。这与王全九等[12]的研究成果相似，都证明了在入渗时间较长的情况下，Green-Ampt模型模拟精度更高。盐碱土由于盐分离子的存在，其入渗性能降低，入渗历时较普通土壤更长[13]，采用Green-Ampt模型更适合描述盐碱土水分运移规律。不同于Kostiakov等经验模型，Green-Ampt模型具有坚实的理论基础，可以不断被修正从而适用于盐碱土入渗。因此采用Green-Ampt模型模拟盐碱土入渗过程具有明显优势，但目前还未有固定的通用于盐碱土入渗的修正Green-Ampt模型。

本文根据盐碱土的入渗特性采用入渗区含水量剖面分布假定，通过扩散率计算得到基质吸力值从而对传统Green-Ampt模型进行修正，建立适用于盐碱土的修正Green-Ampt入渗模型，并采用试验数据验证该模型。修正模型综合考虑盐碱土入渗机理，结合水分入渗过程，进一步提高了入渗预测模型的精度，高精度的水分入渗预测作为基础研究可为盐碱土的改良利用与农业生产提供理论依据与技术支持。

1 基本理论

1.1 Green-Ampt模型基本表达式

Green-Ampt模型针对出现薄层积水时干燥土壤的入渗问题，假定入渗中存在明显的水平湿润锋面，将湿润区与未湿润区分开，入渗时的水分运移符合达西定律。模型基本表达式[3]为

式中i(t)为入渗率，cm/min；Ks为饱和导水率，cm/min；Sf为湿润锋面基质吸力，cm；Zf为湿润锋运移深度，cm；H为土壤表层积水深度，cm。

由水量平衡原理，推得累积入渗量与湿润锋运移深度的表达式为

式中I为累积入渗量，cm；θs为土壤饱和含水率，%；θi为土壤初始含水率，%。

利用式（1）和式（2）推得时间与湿润锋关系式为

式中t为时间，min。

1.2 修正Green-Ampt模型

1.2.1 基本假设与理论

对于Green-Ampt模型，应用时要解决的最重要问题，即确定模型两大参数饱和导水率Ks与基质吸力Sf。在传统模型的实际应用中，由于空气的存在，土壤的饱和区并不能完全被水填满，因此饱和区的实际导水率K0会小于理论上的饱和导水率Ks，地表实际含水率值θ0会小于土壤饱和含水率θs[14-16]。有研究表明(θ0-θi)与K0不准确造成的数据结果差异大于Sf不准确造成的差异，因此确定(θ0-θi)与K0的数值是至关重要的[17]。

本研究对修正Green-Ampt模型作以下假设：

1）考虑到盐碱土由于盐分离子的存在，入渗时长高于普通土壤，甚至出现水分难以下渗的现象[18]，假设试验计划湿润锋深度足够深，入渗时间足够长，认为上层土壤接近饱和，入渗率趋于稳定。则有两个结论：①K0数值等于土壤稳定入渗率ie，为1/2的饱和导水率[19]；② 土壤上层饱和区的地表实际含水率θ0等于入渗时间超过24 h的土壤表层实测含水率θm。

2）由于盐碱土为非饱和土，假定水分到达的区域为入渗区，将入渗区分为湿润区与浸润区，含水量分布如图1所示，湿润区导水率K=ie且含水率θ=θm，浸润区含水率由θm到θi变化。对湿润区作以下假设：①当湿润锋运移深度为L时，湿润区深度为L/α(α的取值范围为1～10)；②有研究证明土壤浸润区的含水率分布采用椭圆曲线描述具有较高精度[20]，因此入渗时用1/4的椭圆曲线描述浸润层含水量变化，温馨等[21]经研究获得湿润区深度为L/2时入渗深度的隐性表达式，本研究将湿润区深度设为L/α，得出不同入渗时刻t(min)下，湿润锋运移深度L(cm)的隐性表达式

式中ie为土壤稳定入渗率，cm/min；θm为土壤表层实测含水率，%；α为表征湿润区深度时使用的参数，无物理意义。

由此，将Green-Ampt模型中的Ks数值替换为稳渗率ie，修正Green-Ampt模型的表达式为

1.2.2 参数推导

根据Philip的研究[22-23]，传统Green-Ampt模型实质上是将土壤水分运动参数近似为δ函数，即用一个含水率处急骤上升的δ函数来近似代替土壤扩散率D(θ)，而扩散率D随含水率发生变化，土壤含水率较大时，扩散率急速增大，因此模型计算的土壤湿润锋吸力Sf值与实际数值有较大差距。Sf值的修正方法本质是用一条D=D’的线性化直线近似表达土壤水分运动参数D(θ)，避免了扩散率D(θ)因含水率的增加而急速上升的现象，从而增加了Sf计算值的准确度。

令D'表示湿润区某种平均的或有效的土壤扩散率，已知Zf与t有近似关系式[24]

使用ORIGIN软件通过最小二乘法拟合试验数据Zf与t，拟合形式为：Zf=λ·t0.5（λ为拟合时使用的参数，无物理意义）。则有D'=λ2/2，通过拟合结果得到D'值。

而D'的表达式为

根据对Green-Ampt模型的两个假设，将土壤饱和导水率Ks替换为稳渗率ie，将土壤饱和含水率θs变为土壤表层实测含水率θm，式（7）可写为

将定值ie、H、θm、θi代入式（8），得Sf值。

综上，Green-Ampt模型修正后两大参数Ks与Sf都可得到准确数值。在入渗时间足够长的情况下，将Ks转换为更易得的稳渗率ie，并通过将土壤水分参数D(θ)近似线性化，经ORIGIN软件拟合后得到更准确的Sf值，避免了含水率增大对D(θ)的影响。

为进一步探究修正模型精度，引用郭向红等[25]建立的Green-Ampt模型模拟盐碱土的入渗过程，比较两种模型模拟效果，确定模拟效果造成差异的原因。郭向红模型与修正模型基本假定相同，因此可引用该模型模拟盐碱土的入渗过程，并探究郭向红模型模拟盐碱土入渗的精度。为了研究不同水头下的水分入渗情况，基于传统Green-Ampt模型的基本假定，即土壤初始含水率分布均匀且存在明显的湿润锋，郭向红等采用入渗率与湿润锋运移深度的倒数呈线性关系这一理论依据，求得概化湿润锋深度，通过拟合入渗率数据与概化湿润锋，求得参数a、b值，计算得饱和导水率Ks与基质吸力值Sf。

将Ks代入式（3），利用MATLAB采用二分法解不同时刻t对应的Zf，将解出的Zf代入式（1），即可求出不同时刻对应的入渗率。

2 材料与方法

2.1 试供土样

试验土壤均取自于内蒙古河套地区沙壕渠灌域，在灌域内随机选取12个采样点，采集0～30 cm深度表层土，经风干、研磨、过筛后得到土样。土壤含水率由烘干法测得，使用pH试纸测得土壤pH值，采用激光粒度仪Mastersizer-APA2000测得土壤颗粒组成，对盐碱土易溶盐离子的含量进行测定。经测定后获取到易溶盐总量与8种主要的易溶盐离子CO32-、HCO3-、SO42-、Cl-、Ca2+、Mg2+、K+、Na+含量。根据盐渍化分级标准的易溶盐总量确定盐碱土的盐渍化程度，12个采样点的盐碱土样品分别为2个轻度盐碱土、2个中度盐碱土、2个重度盐碱土，其他6种均为盐土。因此样品中的轻度盐碱土、中度盐碱土与随机选取的1个重度盐碱土构成了本文所用的5种土壤类型，根据5种试验土样验证修正Green-Ampt模型的适用性，其基本理化参数见表1。

表1 试验土样理化参数Table 1 Physical and chemical parameters of test soil samples

2.2 试验方案

试验地点位于陕西西北农林科技大学旱研院灌溉大厅，试验为一维垂直积水入渗试验，装置图见图2。装置由试验土柱、供水设备和支架组成，试验土柱采用有机玻璃材料制造，柱高70 cm，内径为12 cm，装土高为60 cm，下置透气底板。供水设备为内径10 cm的马氏瓶。试验土柱与马氏瓶外壁均有刻度，以便观察读数。

将试验土样混合均匀，风干后过2 mm筛备用。灌溉用水为咸阳市杨陵区自来水。利用马氏瓶供水，供水水头始终控制为3 cm。在试验过程中，按照先密后疏的时间间隔定时观察数据，记录土柱湿润锋运移深度和马氏瓶水位数据。经预试验确定计划湿润锋为30 cm，即当湿润锋达到30 cm时停止供水，结束试验。

环境温度控制在24 ℃左右，蒸发忽略不计，每种盐碱土入渗试验重复3次。

2.3 数据处理

将修正Green-Ampt模型与郭向红模型计算的入渗率进行对比，分析两者模拟效果的差异。为评价模型模拟精度，将修正Green-Ampt模型模拟值与实测值进行相关分析，并使用决定系数R2与平均绝对误差MAE作为评价指标。采用软件SPSS19.0进行分析。

3 结果与分析

3.1 参数确定

3.1.1 修正Green-Ampt模型

根据式（8）求得土壤水分运动参数Sf。

根据对Green-Ampt模型的假设，认为盐碱土试验计划湿润锋深度足够深，入渗时间足够长，Ks数值等于土壤稳定入渗率ie。

5种盐碱土采用修正Green-Ampt模型计算的Ks与Sf值见表2。

表2 修正Green-Ampt模型Ks与Sf值汇总Table 2 Summary of Ks and Sf values of improved Green-Ampt model

3.1.2 郭向红模型

根据试验方案确定入渗水头为定值，即H=3 cm。求得概化湿润锋深度后，经拟合概化湿润锋深度的倒数与试验入渗率的关系计算Ks与Sf值。5种盐碱土的Ks与Sf值见表3。

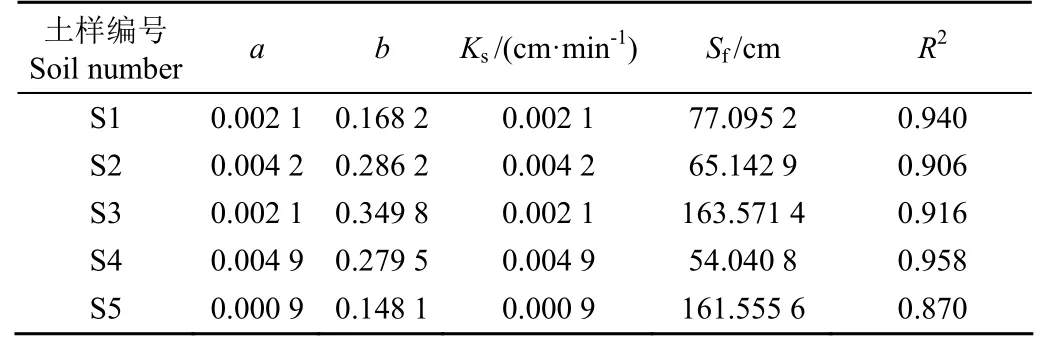
表3 郭向红模型Ks与Sf值汇总Table 3 Summary of Ks and Sf values of Guo Green-Ampt model

3.2 模型参数与含盐量分析

土壤入渗Green-Ampt模型的两大参数Ks与Sf值由土壤性质确定。在灌溉水样一致、装土容重相同的情况下，土壤自身特性是影响模型参数的主要因素，作为盐碱土，盐分含量对土壤的模型参数有重要影响。将修正模型参数值与盐碱土含盐量进行分析。根据土壤中盐分离子电动电位从小到大的排序（Ca2+＜Mg2+＜H+＜NH4+＜K+＜Na+），K+和Na+电动电位大，分散性强而凝聚性弱，即加强土壤颗粒的分散性并降低土壤团聚体的稳定性，较短时间内使土壤的大孔隙崩塌，小孔隙堵塞，降低土壤对水和空气的渗透性，降低导水率，即这两种离子最大程度上会影响土壤入渗能力，改变土壤入渗模型参数。因此取K++Na+与易溶盐总量作为衡量土壤含盐量的两大指标。

5种盐碱土修正Green-Ampt模型参数值与含盐量指标见表4。根据表4可以看出，Ks、Sf与易溶盐总量无明显规律，但是与K++Na+存在一定规律，除S1外其他4种盐碱土的参数值Ks随K++Na+含量的增大而减小，Sf随K++Na+含量的增大而增大。

表4 修正模型参数值与含盐量指标汇总Table 4 Summary of improved model parameter values and salt content index

由于模型参数受K++Na+的影响，选择S2、S3、S4、S5的K++Na+含量分别与Ks、Sf值进行回归分析，分别采用幂函数模型与对数函数模型进行回归估计。决定系数和检验值结果见表5。

表5 饱和导水率、基质吸力与K++Na+含量回归分析结果Table 5 Regression analysis results of saturated hydraulic conductivity, matric suction, and K++Na+ content

从表5可以看出，采用幂函数模型对K++Na+与Ks值进行回归分析，R2值大于0.95；采用对数函数模型对K++Na+与Sf值进行回归分析，R2值大于0.99。因此两种模型拟合的显著性检验都具有统计意义。

3.3 模型验证与对比

3.3.1 入渗率验证与对比

将修正Green-Ampt模型计算的Ks与Sf值代入式（5），郭向红模型通过式（3）采用二分法解出Zf代入式（1），可求出两种模型不同时刻对应的入渗率，将模型计算结果与实测数据进行对比，探究其模拟入渗效果的准确度。5种盐碱土的入渗率比较结果点绘于图3。

如图3所示，修正Green-Ampt模型计算的入渗率在整体上更接近于实测值，特别在曲线的后半段，郭向红模型与实测值差距较大，而修正Green-Ampt模型与实测值更为接近。由图3中S3曲线可见，郭向红模型计算值与实测值差距明显，显著高于实测值，而修正Green-Ampt模型的数据曲线与实测值曲线基本一致。因此根据图3显示，修正Green-Ampt模型的入渗率数据更接近于5种盐碱土的实测值。

将郭向红模型、修正Green-Ampt模型计算的入渗率与实测值进行相关分析，以衡量两组数据的接近程度，见表6。

表6 显示，对于试验所用的5种盐碱土，修正模型计算的入渗率R2平均值为0.983，且58种盐碱土R2值均高于0.95，呈现极强相关性。修正模型模拟值的MAE均小于0.05 cm/min，MAE最大值的平均值分别为0.048和0.029 cm/min。综合R2值与MAE两个指标，修正Green-Ampt模型预测值误差较小，模拟精度较高。郭向红模型入渗率R2平均值为0.932，MAE平均值为0.055 cm/min，总体与实测值存在一定差距，特别在曲线后半段其计算值高于实测值。总体看来，修正Green-Ampt模型模拟的入渗率曲线更接近实测值，更适用于盐碱土入渗分析。

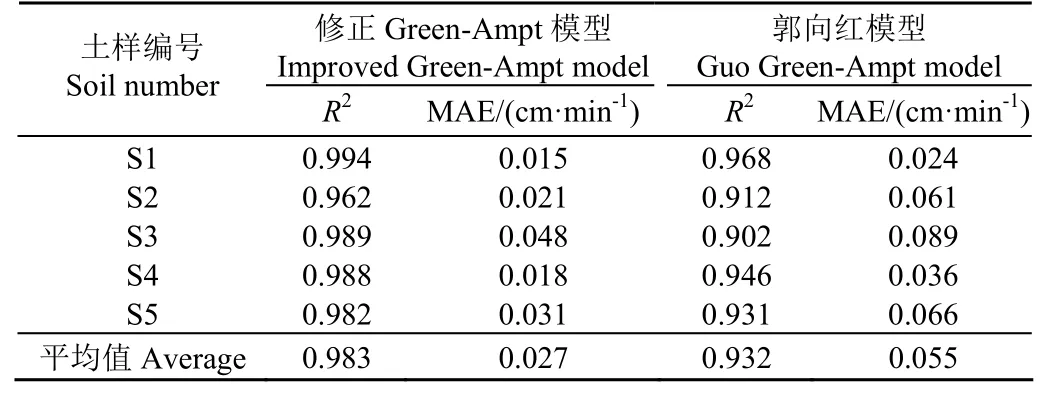
表6 入渗率相关分析结果汇总Table 6 Summary of related analysis results of infiltration rate

3.3.2 湿润锋运移深度验证

因为郭向红模型中的湿润锋为概化湿润锋，因此只利用湿润锋实测值验证修正模型的适用性，不进行两种模型模拟效果的对比。修正Green-Ampt模型的验证是通过MATLAB建立代码表达式（4），α定义为从1到10步长为0.1的循环，精度为0.001，将1种盐碱土的Δθ、t、Sf、K代入计算得91个数组（横轴为α，纵轴为时间），5种盐碱土重复5次操作。将91个数组与对应盐碱土的湿润锋实测值进行相关分析，当α取值为1时与实测值最接近，随着α的增加，实测值与模拟值的差距越来越大，严重偏离实际情况（当α取值为1.1时与实际情况已出现较大差异）。因此，α取值为1，湿润层深度为L。出现此情况是由于所取盐碱土的盐分与土壤质地共同影响。由表1可以得知5种盐碱土的质地偏黏，土壤颗粒中黏粒占据一定比例，黏土在岩土工程中被称为饱和土，水会占据土壤孔隙的绝大部分体积，土壤持水能力强。其次，5种盐碱土中含有大量K+和Na+，两种离子电动电位大，对土壤颗粒的分散作用强，会减弱对下层土壤的导水能力。

将修正Green-Ampt模型所计算的不同时刻的湿润锋运移深度与实测值进行对比，分析模型精度。将5种盐碱土的湿润锋运移深度点绘于图4。

如图4所示，修正Green-Ampt模型与实测值的差异整体上较小，图4中S1曲线显示模拟值与实测值趋势基本相同，S2、S4模拟曲线与实测值比较接近。S3、S5曲线有明显拐点，拐点前模拟值小于实测值，拐点后模拟值大于实测值。将此现象结合盐碱土的盐分离子含量进行分析，K+和Na+分散性强凝聚性弱，降低土壤导水率[26-27]，S3、S5的K++Na+含量分别为1.69、5.33 g/kg，而其他3种土均小于1 g/kg，因此在拐点处盐分向下运动不断累积，土壤水溶液的K+和Na+到达一定浓度，使土壤颗粒分散，导水能力出现明显衰减，湿润锋向下运移的速率减缓。

此外，S5的湿润锋运移距离只到达25 cm，与预期湿润层30 cm出现矛盾。原因在于S5是唯一的重度盐碱土，土壤质地为壤质黏土。黏土持水能力强、易饱和，又由于盐分离子随着水分运动的下移不断累积，堆积形成障碍层，两者共同影响从而使水分无法下渗。

5种盐碱土修正模型计算的R2平均值为0.868，S1的R2最高，为0.952。修正模型计算的MAE平均值为2.639 cm，且5种盐碱土MAE数据均小于3.50 cm，修正模型中S1的MAE值最小，为1.185 cm。分析结果证明修正模型的预测值与实测值较为接近，数据误差较小，其中S1实测值与模型计算值一致性较高。

4 讨论

4.1 S1含盐量与修正模型参数分析

模型参数与含盐量分析中，S1不符合Ks随K++Na+含量的增大而减小、Sf随K++Na+含量的增大而增大的规律。5种盐碱土中S1含盐量指标K++Na+含量最少，而模型参数值Ks却并非最高，原因在于与其他盐碱土相比，S1作为轻度盐碱土，其Ca2+、Mg2+离子含量较高，且pH值为8.10，属碱性。在水分的入渗过程中，土壤胶体上的Ca2+、Mg2+离子被Na+置换到土壤溶液中，从而形成一种微溶物和一种沉淀，分别为Ca(OH)2、Mg(OH)2，这些物质在土壤中大量累积堵塞土壤孔隙，使水分和空气无法透过，降低土壤的导水能力。另外，S1为壤质黏土，与作为重度盐碱土的S5质地相同。而壤质黏土与其他土壤相比，由于土壤颗粒本身含有较多黏粒，在入渗过程中势必会降低土壤的入渗性能[28-29]，使土壤表现出特殊性。

S1修正模型参数值Sf不符合规律的原因在于其黏重的质地。根据国际制土壤质地分类标准，S1中的黏粒（土壤颗粒粒径小于0.002 mm）含量在5种盐碱土中位居首位（表1）。Sf存在一定表达式[6]，说明其值受土壤进气吸力ψb、形状系数n、土壤表层积水深度H与位置水头Z共同影响。对于本文H与Z都是定值，H取3 cm，Z定值为0，而ψb、n与土壤质地关联紧密。一般地说，粗质地砂性土壤或结构良好的土壤其进气值是比较小的，而细质地的黏性土壤其进气值相对较大[30]，S1黏重的质地使其ψb数值变大。土壤孔径分布要取决于土壤质地，质地越黏，土壤形成细小的无效水孔径越多，较大的有效水孔径越少[31]，用RETC软件选用VG公式拟合5种盐碱土的土壤水分特征曲线得到参数n值，S1、S2、S3、S4、S5的n值分别为2.162、2.189、2.306、2.165、2.408，S1的n值最小。S1的ψb数值大且n值小，因此出现了S1的Sf值偏大，不符合规律的特殊现象。

4.2 模型入渗率模拟值对比分析

入渗率验证与对比中，修正Green-Ampt模型模拟精度高于郭向红模型。这是由于修正模型计算的模型两大参数Ks与Sf值比郭向红模型更精确，更接近其理论值。郭向红模型的参数计算误差主要发生在曲线拟合处，即拟合入渗率与概化湿润锋运移深度的关系这一部分，出现误差的原因在于试验数据会受到各种外界因素干扰，特别是在入渗初期，入渗水头会产生波动，土壤入渗情况会受到扰动直至入渗稳定，而在入渗末期由于这5种盐碱土中含有黏土颗粒，甚至会出现入渗率数据非常小、水分几乎无法向下渗透的情况，在曲线拟合时入渗初期与入渗末期的数据都会对曲线拟合的参数值大小产生影响。由于拟合曲线的纵截距等于Ks值，且试验所用盐碱土都为黏壤土，Ks数量级很小，因此入渗数据的微小变化都会使Ks值发生较大改变，Sf受Ks影响数据也会产生偏差。修正的Green-Ampt模型通过将土壤水分运动参数D(θ)线性化，计算出的Sf值更接近理论值，Ks数据由试验实测确定，因此模型计算结果更贴近实测值。但是考虑到两种模型最初的最佳适用条件不同，郭向红模型使用于不同入渗水头下的入渗试验，而本研究的修正模型本就使用于盐碱土的入渗试验，因此该对比具有一定限制性。修正模型计算值与实测值不完全一致是因为：试验数据易受环境扰动且土壤初始含水率极低，因此在入渗初期水分以极快速度湿润土体，入渗率往往会大于模型计算值。

4.3 修正模型模拟误差原因确定

湿润锋运移深度验证中，忽略由于盐分离子影响而使湿润锋出现拐点的S3与S5，其他3种土的模型预测值均小于计算值，即对应时刻的预测值小于试验的湿润锋实测值，原因在于两点：1）湿润区的确定，α定义为从1到10步长为0.1的循环，当α取值为1时模型湿润锋计算值小于实测值，而当α取值为1.1（湿润区为10/11 L）时模型计算值大于实测值，因此存在相对于湿润区占比很小的浸润区；2）在试验开始阶段，表层土壤会以极快速度被润湿，湿润锋快速下移，影响后期湿润锋运移实测值，因此模型计算值通常小于实测值。

4.4 修正模型的限制性

研究盐碱土的入渗特性对于其改良利用有至关重要的意义，目前还未建立盐碱土的入渗模型。由于盐碱土盐分离子的存在使其入渗时长大于普通土壤，采用对长时间入渗模拟具有较高精度Green-Ampt入渗模型模拟盐碱土入渗。本文在传统Green-Ampt入渗模型的基础上根据盐碱土的入渗特性引进扩散率D(θ)对模型进行修正，考虑了土壤中空气的存在并通过线性化表达D(θ)的方法，提高了模型参数的准确性，该研究对加深盐碱土农业灌溉研究与加快盐碱土农业生产起一定推动作用。模型参数受盐碱土自身特性影响，此处探究了含盐量与模型参数的变化规律，发现参数值Ks随K++Na+含量的增大而减小，Sf随K++Na+含量的增大而增大。樊贵盛等[32]通过大田盐碱荒地入渗试验证明了入渗能力、稳定入渗率与K++Na+呈负相关，本文得到的部分结论与之类似。该研究建立的修正Green-Ampt模型经检验可应用于土壤质地较为黏重的盐碱土入渗模型研究中，进行不同盐渍化程度的盐碱土入渗过程模拟，当盐碱土离子成分与试验土样不同时，该模型依然适用。但对于不同土壤质地的盐碱土，如砂土含量极高的盐碱土，该模型具有一定限制性。修正Green-Ampt入渗模型的建立还需进行更加深入的研究，作者将在后期的研究中将此作为重点，保证模型在不同质地土壤类型的广泛应用。