油葵籽粒离散元参数标定与试验验证

郝建军，魏文波，黄鹏程，秦家辉，赵建国

（1. 河北农业大学机电工程学院，保定 071000；2. 河北省张家口市乡村振兴促进中心，张家口 075000）

0 引 言

油葵是中国第三大油料作物，年产量达到250多万t，在农业发展中占据重要地位[1-4]。传统试验方法不能精准分析油葵籽粒在种植、收获机械中的运动过程，使油葵机械化种植与收获装备的相关研究与其他油料作物相比相对滞后，制约了油葵产业的机械化进程[5-6]。近年来，以离散元法为基础的EDEM软件被广泛应用于散体物料运动过程研究，为研究农业物料动力学行为提供了新思路。

对农业物料模型进行仿真试验时，需要对其本征参数与接触参数进行标定[7-11]。马文鹏等[12]、郝建军等[13]、石林榕等[14]、李永祥等[15]分别对苜蓿种子、沙壤土、胡麻籽粒、小麦粉等离散元参数进行分析与标定，为相关物料的仿真提供了可参考的离散元参数。

油葵籽粒体积较小，且形状不规则，仅靠物理试验很难获得其参数。为防止仿真效果失真，合理确定油葵籽粒离散元模型和相关参数具有重要意义。本文通过测定油葵籽粒本征参数，结合三维扫描技术与Hertz-Mindlin接触模型，建立油葵籽粒离散元模型。对油葵籽粒进行物理堆积试验与仿真试验，以堆积角为指标，通过Plackett-Burman试验筛选出对指标影响显著的因素，利用最陡爬坡试验快速寻找各因素最优值所在区间。通过响应面优化试验，建立堆积角与油葵籽粒间静摩擦系数和油葵籽粒间滚动摩擦系数的二阶回归模型，获取可用于离散元仿真的油葵籽粒参数，通过堆积试验和电磁料斗振动试验验证油葵籽粒模型和仿真参数的可靠性，以期为油葵播种、收获等机械化作业及装备研发仿真模拟提供可靠的离散元模型参数。

1 油葵籽粒本征参数测定及离散元模型建立

1.1 三维几何尺寸及分布规律

为准确建立油葵籽粒三维模型，以五点取样法对河北省邢台市金沙河红薯岭基地油葵种植区的矮大头567取样，随机选取500粒，利用111N-101-40型绝对原点数显卡尺（精度0.01 mm）分别测其3轴尺寸（最大长度a、最大宽度b、最大厚度c）[16]，测量结果取平均值（见表1）。

由表1可知，油葵籽粒的最大长度a、最大宽度b、最大厚度c的平均值分别为13.36、6.94、4.63 mm，标准偏差分别为0.435、0.420、0.405，油葵籽粒呈扁长形。

表1 矮大头567油葵籽粒三轴尺寸Table 1 Three-axis dimensions of dwarf big head 567 oil sunflower seeds

1.2 含水率与密度

应用赛多利斯BSA224S型高精度电子分析天平（最小刻度0.1 mg）对随机选取的100粒油葵籽进行称量，重复5次取平均值，得到油葵籽粒百粒质量为9.547 g，采用比重瓶测试法测量100粒油葵籽粒的体积，重复5次取平均值为11.24 cm3。通过计算获得矮大头567油葵 籽粒的密度为849.4 kg/m3。利用B0D-75-Ⅱ型电热恒温干燥箱（济南鑫贝生物技术有限公司）对上述100粒油葵籽粒进行烘干，冷却至室温后采用干基表示法[16]，按照公式（1）计算得出油葵籽粒平均含水率为10.13%。

式中Md为干基含水率，%；wm为物料中所含水分的质量，g；ms为物料中所含干物质的质量，g。

1.3 泊松比

泊松比是指材料在单向受拉或受压时，横向正应变与轴向正应变的绝对值之比，亦称横向变形系数，反映材料横向变形的弹性常数。

从上述样品中随机选取10粒油葵籽粒，分别用衡翼HY-0580型万能材料拉压力试验机沿油葵籽粒厚度方向施加压力（加载速度0.1 mm/s）至油葵籽粒发生破裂。由万能材料拉压力试验机读取油葵籽粒厚度方向（轴向）正应变的变形量，利用绝对原点数显卡尺测量宽度方向（横向）正应变的变形量[17]。按公式（2）计算油葵籽粒泊松比。本研究10次试验结果平均值为0.413。

式中ν为泊松比；e′为油葵籽粒宽度方向的变形量，mm；e为油葵籽粒厚度方向的变形量，mm；1W为加载前油葵籽粒的宽度，mm；W2为加载后油葵籽粒的宽度，mm；1L为加载前油葵籽粒的厚度，mm；2L为加载后油葵籽粒的厚度，mm。

1.4 弹性模量与剪切模量

弹性模量是用来衡量材料抵抗弹性变形能力大小的标尺。试验时，首先利用绝对原点数显卡尺测量随机选取的10粒油葵籽粒受压前厚度（L1），将其自然放置于衡翼HY-0580型万能材料拉压力试验机的圆形平台上，使用直径5 mm的圆形压头，以5 mm/min的加载速度对油葵籽粒施加载荷，并读取力（F）-变形（LΔ）数据，对10粒油葵籽粒分别重复上述试验，由公式（3）～公式（5）计算出弹性模量平均值为304.69 MPa，剪切模量平均值为107.82 MPa。式中E为弹性模量，MPa；F为油葵籽粒受到的轴向载荷，N；A为接触面积，mm2，圆形压头直径5 mm，与油葵籽粒接触面积为0.193 mm2；ε为应变；LΔ 为油葵籽粒受压后的变形量，mm；G为剪切模量，MPa；ν为油葵籽粒泊松比。

1.5 基于三维扫描的油葵籽粒离散元模型建立

油葵籽粒的外形是不规则体，常规建模方法无法精确还原其真实特征。为准确建立油葵籽粒三维模型，提高仿真试验的真实性，本文选取长宽厚均接近平均值的油葵籽粒（如图1a）为研究对象，应用三维扫描技术，通过GD-3DScan四目三维扫描仪（测量精度0.001～0.05 mm，单幅扫描点数为2 620 000，平均点距为0.15～0.3 mm）扫描油葵籽粒外轮廓，精确获取油葵籽粒外表面三维坐标，生成点云数据（如图1b），然后将点云数据导出到Geomagic Studio软件中进行合并拼接处理得到油葵籽粒模型，最后将油葵籽粒模型导入GOM Inspect软件，对尖锐、噪点进行锐化处理得到油葵籽粒三维模型（如图1c）[18-20]。将油葵籽粒三维模型导入EDEM2020软件中，设置颗粒属性并将平滑值设置为5，最小颗粒半径设置为0.3，运用EDEM2020软件的自动填充方法得到由67个不等径颗粒组成的油葵籽粒离散元模型（如图 1d）。

2 接触参数测定

2.1 静摩擦系数

2.1.1 油葵籽粒与其他材料之间的静摩擦系数

静摩擦系数是物料所受最大静摩擦力与法向正压力的比值，可以很好地表达物料与接触固体表面的摩擦性质[21]。由于油葵种植与收获装备的主要材质为钢板、有机玻璃，故本研究采用斜面法测量油葵籽粒与钢板、有机玻璃之间的静摩擦系数，使用H69020101型数显倾角测量仪（精度为0.05°）测量试验过程中的倾斜角度，如图2所示。油葵籽粒属于散体物料，籽粒尺寸较小，易翻滚。为防止油葵籽粒翻滚，获取更加准确的静摩擦系数，试验时，将4粒油葵籽粘接在一起重复进行10次静摩擦系数测量试验。试验开始时钢板、有机玻璃分别置于水平位置，调节角度调节器，使钢板、有机玻璃绕其一侧缓慢转动，直至油葵籽块开始沿板向下滑动。利用高速摄影机捕捉油葵籽粒块开始滑动时钢板、有机玻璃倾斜角度，并求10次重复试验的倾斜角平均值α。按照公式（6）分别求出油葵籽块与钢板、有机玻璃的静摩擦系数，结果如表2所示。

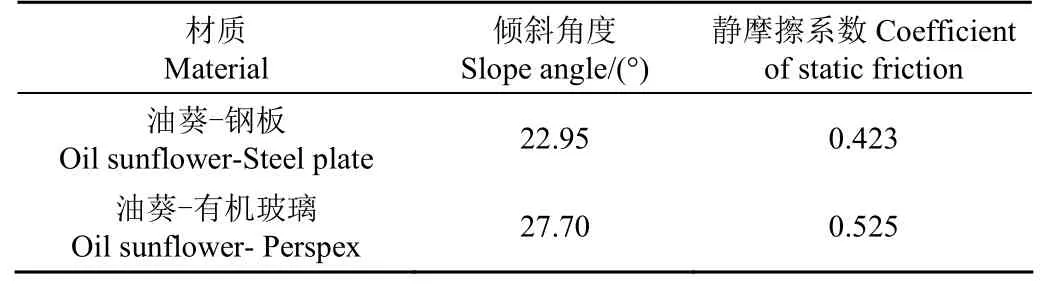
表2 静摩擦系数计算结果Table 2 Calculation results of static friction coefficient

2.1.2 油葵籽粒间的静摩擦系数

油葵籽粒表面为不规则曲面，利用油葵籽粒本体很难完成油葵籽粒间静摩擦系数的测量。为便于测量，参照文献[10，14]方法，试验时利用双面胶将油葵籽粒粘在透明有机玻璃试验板上，粘贴时尽可能使油葵籽粒外壳排布紧密。试验时，将油葵籽粒置于水平放置的试验板上，调节角度调节器，使试验板绕其一侧缓慢转动，记录油葵籽粒开始沿试验板向下滑动时试验板的倾斜角度。求得10次重复试验油葵籽粒间静摩擦系数平均值为0.569。

2.2 堆积试验

散体物料在形成堆积角的过程中存在多种复杂的运动状态，可较好地表征散体物料散落、流动和摩擦等特性[16]。堆积角是物料运输、储藏、收获、播种等环节的重要基础数据[16,22-25]，针对不同物料特性发展出了注入法、倾斜法、圆筒提升法等堆积角测量方法。经预试验对比，表明利用圆筒提升法进行试验时，油葵籽粒的散落性能较好且操作便捷，故本文采用圆筒提升法进行油葵籽粒物理堆积试验，试验装置如图3所示。

试验前，利用直径4～6 mm的标准筛将大小接近油葵籽粒离散元模型的油葵籽粒筛分出来用于堆积试验[26-27]。试验时，将不锈钢圆筒内填充满油葵籽粒，利用万能材料拉压力试验机的卡具夹持圆筒。通过改变不同的提升速度进行预试验，结果表明提升速度为1m/s时，油葵籽粒更容易达到坡面稳定状态，故本研究以1 m/s的速度匀速提升圆筒，0.25 s后停止提升，待所有油葵籽粒静止且油葵籽粒坡面稳定时，利用摄像机对粒堆正侧两面进行垂直拍照。为减少人工测量误差，利用MATLAB对试验得到的堆积角图像进行处理[28]。具体处理方法为：先对原始图像进行灰度处理，选定合适的阈值进行二值化处理，利用bwperim函数对二值图像进行轮廓提取。由于bwperim函数提取外轮廓时，会将图形区域内部的孔洞所围成的内部边缘也提取出来，故使用imfill函数将内部边缘做填洞和膨胀处理，得到完整的边缘轮廓。将边缘轮廓导入Origin中，利用图像数字化工具将边缘轮廓转化为坐标数据并进行线性拟合，将线性拟合得到的斜率转化为角度，即为油葵籽粒物理堆积试验的堆积角。轮廓提取过程如图4所示，将上述试验重复10次（结果见表 3），求其平均值得到油葵籽粒物理堆积试验的堆积角θ为48.858°。

表3 油葵籽粒堆积角测量结果Table 3 Measurement result of oil sunflower seed stacking angle

2.3 基于Plackett-Burman试验的最陡爬坡试验

Plackett-Burman试验通过比较各因子2水平的差异与整体的差异来确定各因子的显著性，以快速筛选出对响应值影响显著的因子。本文采用Design-Expert V8.0.6的Plackett-Burman模块，以油葵籽粒堆积角为响应值，筛选出对油葵籽粒堆积角影响显著的因子，分别用X1～X9表示，设置2个虚拟参数，分别用X10和X11表示。每个参数设置高（+1）、低（-1）水平，结合文献[6，12，14，15，19，29-31]并根据本文试验与仿真预试验确定各参数的取值范围，结果如表4所示。设置3个中心点，共15组试验，每组试验重复3次求平均值。Plackett-Burman试验方案和结果如表5，试验结果方差分析如表6。

表4 Plackett-Burman试验参数列表Table 4 Parameters of Plackett-Burman test

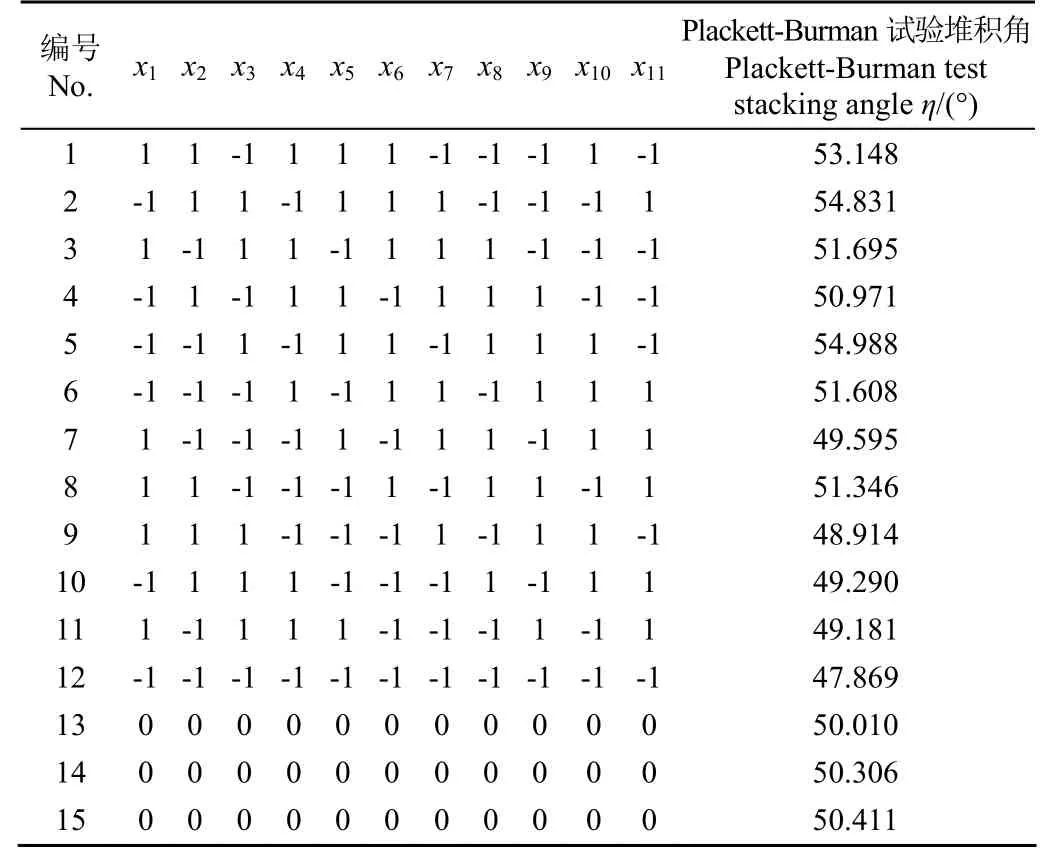
表5 Plackett-Burman试验方案与结果Table 5 Design and results of Plackett-Burman test scheme

由表6可知，该模型P<0.05、决定系数R2=0.96，表明该回归模型显著，且能较好地预测各参数变化趋势。X1、X2、X3、X4、X7、X8、X9对堆积角影响较小，贡献率均小于5%；X5对堆积角的贡献率达到19.88%、X6对堆积角的贡献率高达65.66%，表明X5和X6对堆积角的形成影响极大。通过比较各参数的F值大小，得到各参数对堆积角影响的主次顺序为X6、X5、X1、X3、X2、X8、X7、X4。故选取对堆积角贡献率较大和影响较显著的X5和X6，在后续的爬坡试验与响应面寻优试验中进行寻优，X1、X2、X3、X8选用以物理试验得出的值，其余参数采用表4中数值的中间水平。X5和X6的标准化效应值均大于0，故其对堆积角的影响为正效应，在后续的爬坡试验中，呈正效应的因素以固定步长逐步增大。以上述选定的参数为试验因子，进行最陡爬坡试验并由式（7）计算出最陡爬坡试验堆积角β与2.2节物理试验堆积角θ的相对误差Y，最陡爬坡试验设计及结果如表 7所示。

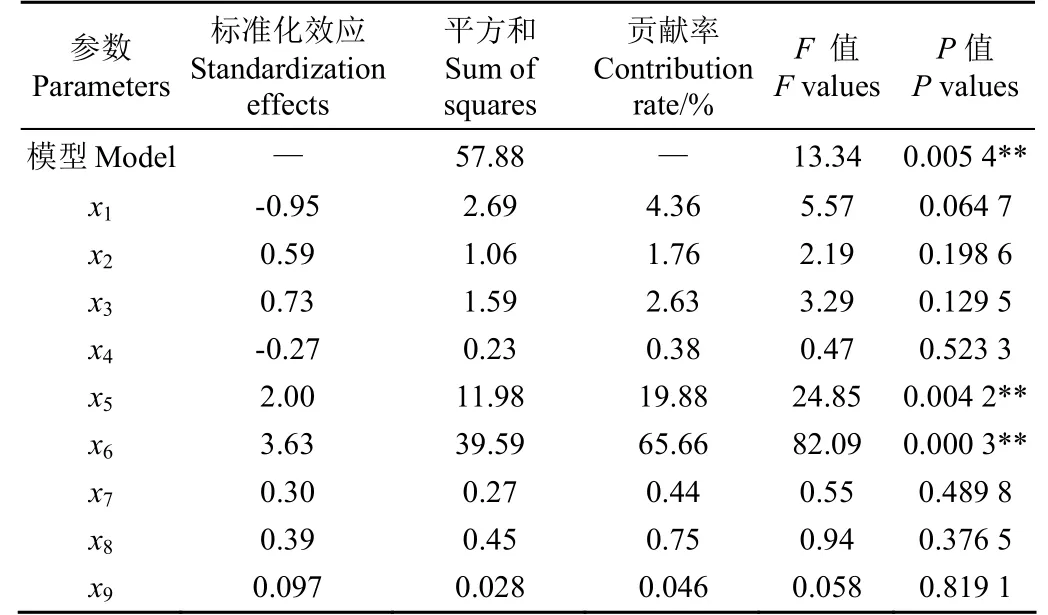
表6 Plackett-Burman试验参数显著性分析Table 6 Analysis of significance of parameters in Plackett-Burman test

由表7可知，随着X5、X6的增大，最陡爬坡试验堆积角β与物理试验堆积角θ的相对误差呈先减小后增大趋势，且在试验2参数下相对误差最小。故选取试验2参数为中间水平，以试验1参数、试验3参数分别为低水平、高水平进行后续的响应面寻优试验。油葵籽粒间静摩擦系数与动摩擦系数取值区间分别为0.369～0.569、0.03～0.115。

表7 最陡爬坡试验方案与结果Table 7 Test design scheme and results of path of steepest ascent method

2.4 响应面寻优试验及回归模型建立

根据上文最陡爬坡试验得到的油葵籽粒间静摩擦系数与动摩擦系数取值区间，应用Design-Expert V8.0.6进行中心复合试验设计。对11组参数组合进行堆积角试验，其中3组为中心水平重复试验，探究油葵籽粒间静摩擦系数(X5)与动摩擦系数(X6)对响应面寻优试验的堆积角(φ)的影响效果。因素编码值与中心复合试验结果如表8所示。

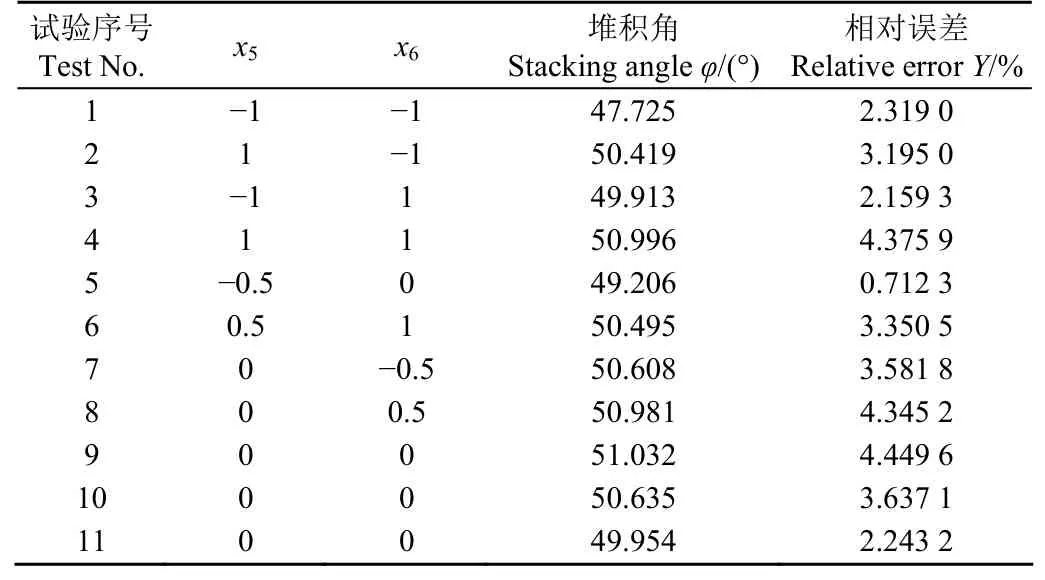
表8 中心复合试验方案及结果Table 8 Center compound test design and results

通过对表8的数据进行二元回归拟合，建立堆积角(φ)与油葵籽粒间静摩擦系数(X5)和动摩擦系数(X6)的回归模型，如式（8）所示。

由方差分析结果表9可知，该回归模型P=0.007 6，失拟项P=0.926 5，决定系数R2=0.925 5，回归模型极显著，失拟项不显著，决定系数接近1，表明该回归方程拟合得较好。变异系数（CV）越大时试验数据的可靠性越差，该模型的变异系数（CV）仅为0.76%，表明该试验结果可靠性较高。利用Design-Expert软件进行中心复合试验时，精确度大于4模型才具有较好的预测性[32]，该模型的精确度为12.363，表明该模型可以较好地预测油葵籽粒的堆积角。由表9可知，X5对油葵籽粒堆积角影响极显著，X6和对油葵籽粒堆积角影响为显著，影响显著性由大至小的排序为：试验因子X5、X6与指标之间存在二次非线性关系，且交互作用对指标的影响不显著，堆积角响应曲面如图5所示。

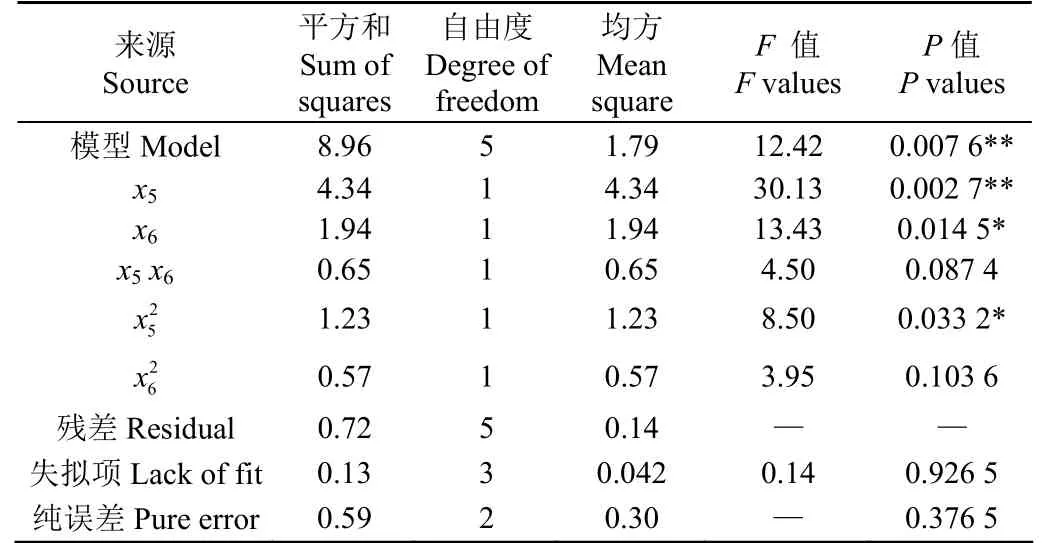
表9 响应面寻优试验回归模型方差分析Table 9 Analysis of variance in regression model of responsesurface optimization test

3 验证试验

3.1 堆积角验证试验

运用Design-Expert V8.0.6的Optimization-Numerical优化功能，以油葵籽粒物理堆积试验所得的堆积角为目标进行寻优，得到25组优化解。对优化解进行仿真试验，将仿真试验结果与物理堆积试验结果进行对比，找出与物理堆积试验堆积角大小、形状最为相似的一组优化解，即油葵籽粒间静摩擦系数为0.41和动摩擦系数0.05。将该组优化解做5组重复仿真试验，求其平均值得到该参数组合下堆积角为48.976°，与物理堆积试验得到的堆积角误差为0.24%。仿真试验与物理试验的对比如图6所示，结果表明，在优化后的仿真参数下，堆积角仿真试验结果与堆积角物理试验结果无显著差异，两者的堆积角的形状与角度相似度高，表明本组仿真参数设置准确。

3.2 电磁料斗振动验证试验

电磁振动料斗垂直方向上下微幅和水平方向扭转复合的振动方式可使油葵颗粒处于动态过程，颗粒间及颗粒与料斗间产生复杂的接触力，类似于实际生产过程（例如振动筛选机械、播种机械等）产生的使颗粒运动的条件。因此，在EDEM中为油葵籽粒模型和料斗模型添加本研究标定的油葵籽粒本征参数与接触参数，基于电磁振动给料器设计不同工作电压（正弦交流电，190～250 V）下油葵籽粒振动验证试验，验证离散元模型和仿真参数的准确性与合理性。试验装置如图7所示，试验时，首先在料斗内添加油葵籽粒，打开已调节好工作电压的控制器开关，并开启高速摄影机对料斗内油葵籽粒的运动进行录像。料斗在电磁力的作用下产生振动频率为50 Hz的垂直方向正弦微幅振动和水平方向正弦圆周振动，给油葵籽粒持续的螺旋激振力，对油葵籽粒做功。油葵籽粒在持续激振力作用下向料斗内壁方向运动，进入螺旋轨道并沿螺旋轨道向出料口运动。待油葵籽粒从出料口均匀排出后，计算1 min内落入集料罐内的油葵籽粒质量，并计算质量流率，每个工作电压重复5次试验求其平均值。

电磁振动装置的作用是为料斗施加激振力，使料斗产生微小的螺旋圆周振动，该振动可分为频率为50 Hz的水平圆周振动和垂直振动，可在EDEM的“Add motion”选项中为料斗模型添加“Add sinusoidal rotation kinematic”和“Add sinusoidal translation kinematic”运动函数，设置与物理试验相同的频率和振幅来模拟电压变化，故在仿真试验中只需建立料斗模型，其余装置进行简化。在SolidWorks中建立料斗模型导入EDEM软件中，为料斗添加振动频率均为50 Hz的水平圆周方向和垂直方向的正弦运动，振幅分别为0θ和Z0，0θ和Z0的关系如公式（9）[33-35]。通过电磁涡流传感器检测料斗与探头端面相对位移变化，将得到的信号转化为垂直振幅大小，根据公式（9）计算出不同工作电压下垂直振幅（Z0）对应的角振幅（0θ），如表10所示。工作电压越大，料斗的振幅就越大，故通过改变振幅大小可模拟工作电压的变化，依据表10，通过改变料斗模型的垂直振幅和角振幅来模拟电压的调节。试验时，待料斗模型内生成的油葵颗粒与物理试验质量相同时，开始振动模拟，在后处理模块输出1min内落入集料罐内的油葵籽粒质量并计算质量流率。仿真试验油葵籽粒分散前、分散后和在螺旋轨道上输送的3种运动状态如图8所示。

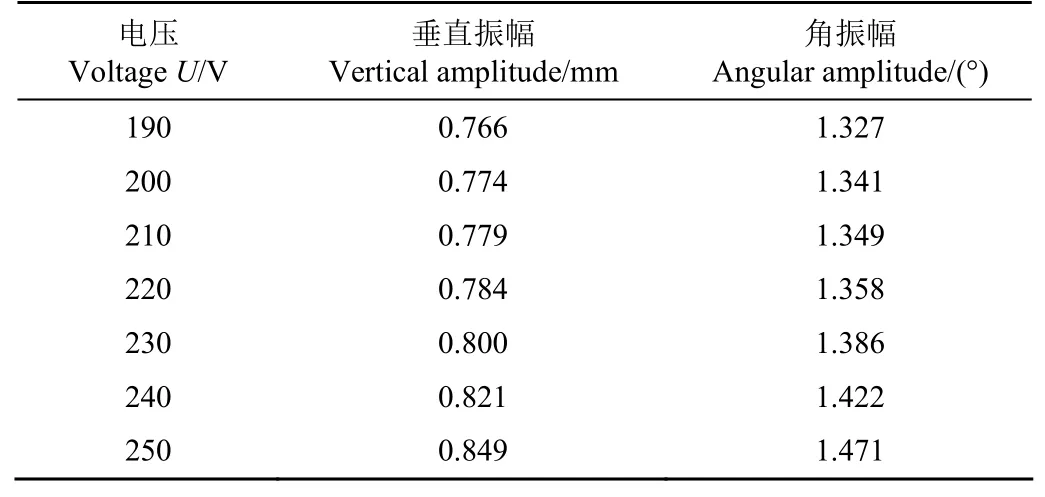
表10 工作电压对应的垂直振幅和角振幅Table 10 Vertical amplitude and angular amplitude corresponding to working voltage

式中Z0为料斗的垂直方向振幅，mm；Ar为弹簧安装点到原点的距离，mm；0θ为料斗的水平圆周方向的角振幅，(°)；Aφ为弹簧安装角，(°)。

物理试验与仿真试验振动过程中不同工作电压下产生的工作电压-质量流率曲线如图9所示。不同工作电压下油葵籽粒物理试验与仿真试验的质量流率曲线的相关系数为0.998，2条曲线变化趋势基本一致，且相关性较强。在工作电压小于230 V时，随着工作电压的增大，质量流率均呈明显的增长趋势，但当工作电压大于230 V之后，增大工作电压对质量流率的影响均不明显。对物理振动试验过程进行录像帧回放，观察分析发现油葵籽粒在料斗的螺旋轨道上做定向有序的连续滑移运动，且靠近出料口的油葵颗粒比料斗底部的油葵颗粒上下跳动程度小。当工作电压大于230 V时，油葵籽粒在螺旋轨道上产生强烈碰撞，跳动程度明显增强，一些油葵籽粒从轨道掉落回料斗底部，重新进入螺旋轨道排序输送，故当工作电压大于230 V时质量流率增长趋势变缓，此过程与仿真动画中油葵颗粒的状态相符。综上可知，该油葵籽粒模型和接触参数合理可用于后续的仿真试验。

4 结 论

1）通过试验对油葵籽粒物理特性参数进行测定。矮大头567油葵籽粒长、宽、厚的平均值分别为13.36、6.94、4.63 mm，且三轴尺寸均符合正态分布，密度、含水率分别为849.4 kg/m3、10.13%，泊松比、弹性模量和剪切模量分别为0.413、304.69和107.82 MPa。

2）利用三维扫描逆向建模技术扫描得到油葵籽粒的三维模型；在EDEM中，以Hertz-Mindlin接触模型为基础，运用自动填充方法得到由67个不等径颗粒组成的油葵籽粒离散元模型，通过试验证明了该模型的合理性。

3）根据圆筒提升法进行油葵籽粒物理堆积试验，利用MATLAB对堆积角图像进行处理，得到边缘轮廓，进行线性拟合得到堆积角为48.858°。通过Plackett-Burman试验与最陡爬坡试验快速筛选出对油葵籽粒堆积角影响显著的因子为油葵籽粒间静摩擦系数和油葵籽粒间动摩擦系数。应用Design-Expert V8.0.6进行中心复合试验设计，建立2个显著性因子与堆积角的回归模型。显著性因子与堆积角之间存在二次非线性关系，且交互作用对堆积角影响不显著。

4）以油葵籽粒物理堆积试验堆积角为目标进行寻优，得到显著性因子较优组合为油葵籽粒间静摩擦系数为0.41和动摩擦系数为0.05。堆积角仿真试验测得该参数组合下堆积角为48.976°，与物理堆积试验得到的堆积角误差为0.24%，两者堆积角的形状与角度相似度高；基于电磁振动给料器设计了不同工作电压下油葵籽粒振动的物理试验与仿真试验，结果表明不同工作电压下油葵籽粒物理试验与仿真试验的质量流率曲线的相关系数为0.998，2条曲线变化趋势基本一致，相关性较强。且物理试验与仿真试验中油葵籽粒动态运动过程相符。以上验证试验的结果表明，标定结果真实可靠，可为油葵播种、收获等阶段机械化作业的仿真提供参考。