基于贝叶斯框架下copula函数的干旱特征分析

段奕多 金琳

摘 要：以汾河流域为研究对象，基于SPI采用游处理论提取干旱特征，采用copula函数模拟干旱特征。结果表明：参数值为2.05的Gumbel copula为模拟汾河流域干旱历时和干旱烈度相依结构的最优copula函数;通过比较拟合效果，MCMC模拟参数估计的精度明显优于常用的局部优化方法;汾河流域秋冬季干旱频繁，年际变化呈现旱涝交替趋势，在研究期（1960—2010年）内共发生54次干旱事件，其中最严重的干旱事件重现期为90年一遇，该研究可为汾河流域的干旱预警机制提供参考。

关键词：汾河流域;贝叶斯框架;copula函数;干旱频率

中图分类号 P426 文献标识码 A文章编号 1007-7731（2021）15-0185-06

Analysis of Drought Characteristics based on Copula in Bayesian Framework

DUAN Yiduo et al.

（College of Water Conservancy and Civil Engineering， Northwest A & F University， Yangling 712100， China）

Abstract： In this paper， Fenhe River Basin is taken as the research object. Based on SPI， drought characteristics are extracted by using the theory of run and stimulated by Copula. The results show that the Gumbel Copula with a parameter value of 2.05 is the best copula function to simulate the correlation between drought duration and drought intensity in Fenhe River Basin; by comparing the fitting results， the accuracy of MCMC simulation parameter estimation is obviously better than the common local optimization method; during the study period， there are total 54 droughts occurred and the most severe drought occurred once in 90 years in Fenhe River Basin. This study can provide a reference for the drought early warning mechanism in Fenhe River Basin.

Key words： Fenhe River Basin; Bayesian framework; Copulas; Drought Frequency

近年來，受全球变暖等影响，气候和环境发生了重大变化[1]，干旱事件发生频率增加，造成的危害程度也增大。受地理环境和气候特征影响，我国是一个干旱灾害频发的国家[2]，据统计，在过去的不到30年中，我国因干旱导致的粮食减产达252亿kg，因此对于干旱事件的研究十分重要。在干旱灾害的研究内容中，旱灾管理一直是学者们重点关注的方面，准确识别干旱事件，并分析干旱事件的重现期，有助于提高农业抗旱的能力，从而减轻农业受干旱灾害的影响。

干旱事件是时空连续的具有多维特征的事件，且各个变量之间往往有密切联系[3]，只针对单变量的统计分析难以提供全面的水文信息，基于此，copula函数被引入对于干旱特征的多元分析中[4]。多年来，copula函数在水文和气候方面的研究中已经得到了广泛应用，例如多变量水文事件的频率分析、水文事件组合分析、水文预报等方面，但大多数水文研究往往局限于固定几个copula（即Gaussian、t、Frank、Gumbel和Clayton）[4-7]。研究人员从以常用的copula作为备选，进行拟合优度评价，从中选出拟合效果最优的一个，这就使得copula函数的运用在选择方面受到了局限。在实际中，采用不同的copula函数，计算结果会有很大的差异，选择最合适的copula函数是运用copula函数分析干旱频率的基础，在研究过程中研究者应尽量扩大对模型的研究范围，尝试分析新的模型。此外，对于copula函数参数的估计，目前大多数学者采用极大似然法[7，8]，这种方法简单有效，但容易出现局部最优的情况，并且也无法定量计算出估算频率的不确定性区间，尤其是在以资料年限短的资料为对象进行分析的情况下，这种方法得出的分析结果可靠性难以判断。本文采用一种贝叶斯框架下的copula函数方法建立干旱历时-干旱烈度的联合概率分布，基于多元copula分析工具箱（Multivariate Copula analysis toolbox，MvCAT），考虑25种copula函数，包括现有水文文献中没有充分考虑过的copula函数种类，在贝叶斯框架下使用马尔科夫链蒙特卡洛模估计copula函数的参数，绘制copula的后验参数分布并估计参数的不确定性，比较各项拟合评价指标，讨论得出最优copula函数，从而基于此分析流域多年来的干旱情况。

汾河流域是山西省工业集中、农业发达的主要地区，流经省内6市29县，流域面积占全省面积的25.5%，水资源总量占全省水资源量的27.2%，汾河是山西省省内第1大河，汾河流域的农业和工业生产值占山西省的50%以上。近年来，汾河流域干旱事件频发，水文干旱情势严峻[9]，研究汾河流域的干旱特征对于山西省水资源优化配置、流域生态管理等具有一定的参考意义。

1 研究材料与方法

1.1 数据来源 为收集识别干旱事件的样本，本研究选用标准降雨指数（Standardized Precipitation Index）SPI作为干旱指标，根据游程理论识别干旱事件的历时和烈度。基础数据为汾河流域1960—2020年的逐月降雨值，来源于国家气象科学数据中心（http：//data.cma.cn），资料完整，具有可靠性。选取的水文站为：太原站、介休站、临汾站和侯马站，分别位于流域的上、中、下游、中下游。为保证SPI计算准确，资料时间尺度跨越了60年，代表性得到保证，在此时间序列中共识别到54次干旱事件。

1.2 研究方法

1.2.1 Copula函数 Copula是一种构建多个随机变量联合分布的函数方法[10]，在[0，1]區间内服从均匀分布。使用Copula函数分析双变量的联合分布时，首先要建立单变量概率分布函数，再通过Copula函数把随机向量X1，X2……Xn的联合分布函数F（x1，x2，…xn）与各自的边缘分布函数FX1（x1），…，FXn（xn）相连接的连接函数，即函数C（u1，u2，…，un），使得

F（x1，x2，…xn）=C[FX1（x1），FX2（x2），…FXn（xn）] （1）

式中：x1，x2，…xn为观测样本，Fx为边缘分布函数，C为n维Copula函数

本研究基于多元copula分析工具箱，使用25种copula函数对观测数据进行拟合并进行拟合优度评价，最终选取排序结果中排名前5的copula函数（Gumbel、Roch-Alegre、BB1、BB5、Tawn）和水文中常用的5个copula（Gaussian、t、Clayton、Frank、Gumbel）进行后续讨论。

1.2.2 拟合优度评价 模型拟合优度评价常用的指标有最大似然值、Nash-Sutcliffe效率（NSE）和均方根误差（RMSE），但这些指标只关注最小化观测和模型模拟之间的残差，因此本研究中增加了Akaike信息准则（AIC）和贝叶斯信息准则（BIC），根据式（2）～（8）计算。这些指标中，AIC考虑了模型的复杂性，BIC考虑了模型的复杂度和观测的数量。RMSE可以量化copula函数模型建立时存在的潜在不确定性，在观测数据有限的情况下，这对于结果的准确性很重要。模型复杂性越高即模型越灵活，也会更好地拟合观测数据，但可能会导致模型的过度约束。与似然值相比，AIC考虑了模型的复杂性和误差残差的最小化，并提供了1种更稳定的模型预测质量度量，通过根据参数个数增加1个惩罚项，避免了过度约束的问题。

计算方法：

1.似然值

l（θ|[Y]）=[i=1n12πσ2][exp][-12σ-2[yi-yi（θ）]2] （2）

式中：l（θ|[Y]）为似然函数，[Y]为观测变量的联合概率分布，σ为误差标准差的估计值，θ为估计参数，yi为观测变量

2.贝叶斯信息准则（BIC）

MSE=[1n-1i=1n（Pei-Pi）2] （3）

BIC=nln（MSE）+ln（n） （4）

3.纳什效率系数（NSE）

NSE=1-[i=1n（Pei-Pi）2i=1n（Pei-Pi）2] （5）

4.均方根误差（RMSE）

RMSE=[MSE] （6）

5.信息准则（AIC）

AIC=nln（MSE）+2 （7）

[Pei=mi-0.44n+0.12] （8）

式（2）～（5）中：n为样本的容量，[Pei]为联合的经验频率，[Pi]为联合分布的理论频率，mi为实测样本中满足D≤di且S≤si的个数。

AIC、BIC值越低，拟合效果越好。RMSE和NSE的取值范围分别是RMSE∈[0，∞];NSE=1，NSE∈[-∞，1]，RMSE值越低，拟合效果越好;NSE越接近1，拟合效果越好，函数的参数范围对它们没有影响。此外，本文还计算了蒙特卡洛模拟p值，如果p≤0.05，则否定原假设;如果p>0.05，则原假设合理。

1.3 贝叶斯分析 贝叶斯分析是一种模型推理和不确定性量化的有效方法，成功应用于水文学在内的各个领域[11]。当新的观测样本被提供时，贝叶斯定理首先计算假设的先验概率，将模型建立中的所有不确定性归结为参数，然后根据以下方法估算模型参数的后验分布。

p（θ|[Y]）=[P（θ）P（Y|θ）P（Y）] （9）

似然函数：

l（θ|[Y]）=[i=1n12πσ2][exp][-12σ-2[yi-yi（θ）]2] （10）

为简化计算，对式（10）进行简化为：

l（θ|[Y]）=[--n2ln（2πσ2）-12σ-2i=1n[yi-yi（θ）]2] （11）

参数后验分布：

P（θ|[Y]）[∝]P（θ）P（[Y]|θ） （12）

式（9）～（12）中：P（θ）和P（θ|[Y]）分别表示参数的先验分布和后验分布，σ为观测误差的标准查估计值，是水文中最广泛使用的校准标准[12]，θ为估计参数Y表示copula函数计算的概率值，[Y]表示观测样本的联合概率。P（[Y]|θ）表示似然函数，P（[Y]）为常量，在分析中可以忽略不计。Bayes方程虽然结果准确，但是存在求解困难的局限，因此在计算过程中常使用马尔科夫链蒙特卡罗算法进行后验分布的取样。

1.4 马尔科夫链蒙特卡罗模拟 马尔科夫链蒙特卡罗算法（MCMC）是1种从高维的、复杂的分布中进行抽样的统计方法，用来描述基于贝叶斯框架的后验参数分布[13]。混合演化MCMC的优势在于智能起点的选择，采用自适应采样算法（Adaptive metropolis，AM）、差分演化算法（Differential evolution，DE）和斯诺克更新算法来计算可行域，实现在1次计算中，同时采用多个起点，搜索多个计算空间，形成多条计算链，找到全局最优解的估计值和参数的后验分布。在计算时，将样本随机分配给n个Copula函数，并选择似然值最高的样本作为马尔可夫链的起点。与目前copula函数参数估计常用的局部优化算法相比，MCMC算法计算范围更广，从多个起点出发因此可以确保估计的参数为全局最优，并可以描述参数的不确定性[13]。

2 结果分析

2.1 Copula函数

2.1.1 拟合优度评价 模型的选择一般基于拟合优度评价，常用的指标有最大似然值、Nash-Sutcliffe效率（NSE）和均方根误差（RMSE），除此之外，本研究还选取了Akaike信息准则（AIC）、贝叶斯信息准则（BIC）作为参考，计算结果见表1。

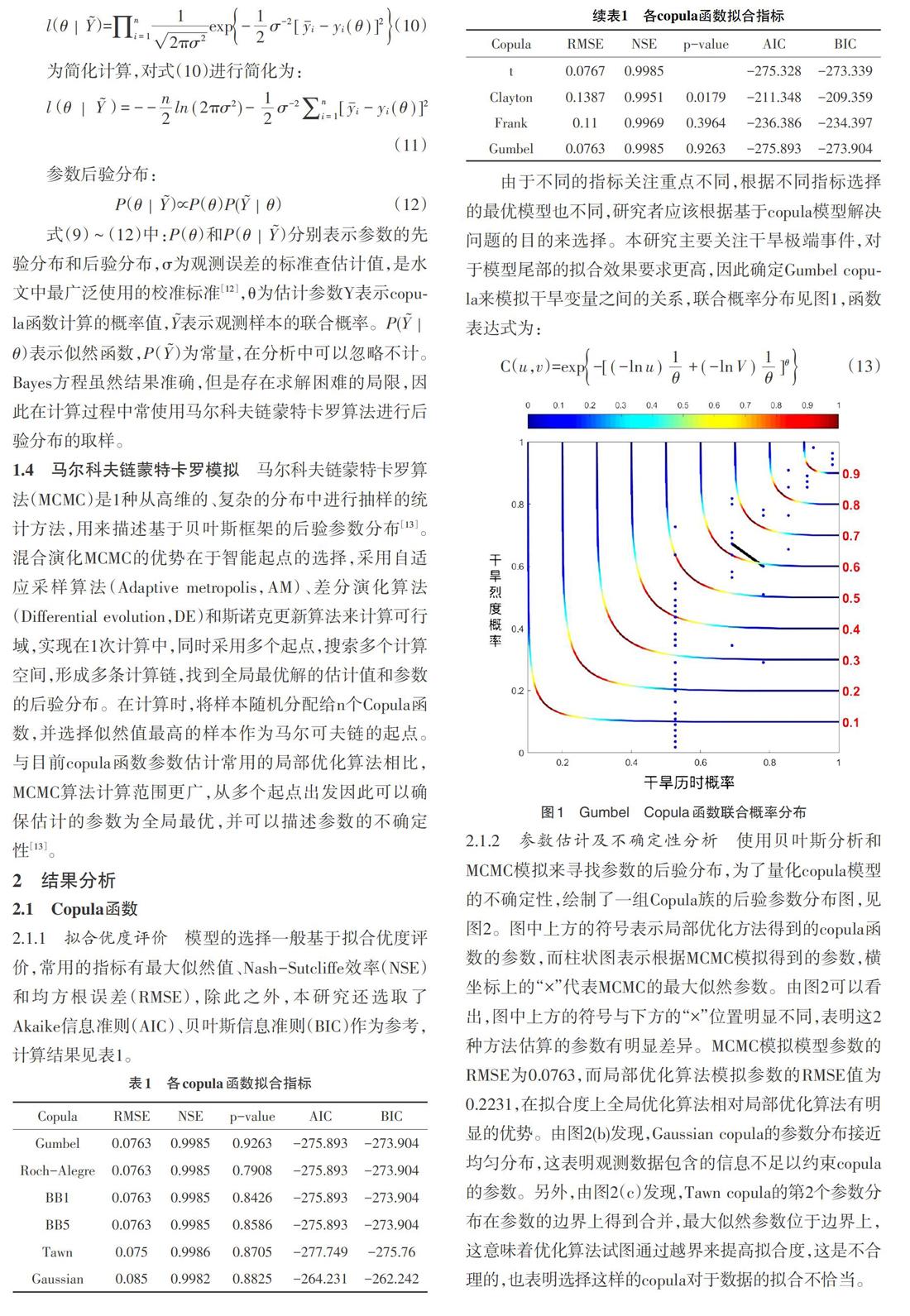
由于不同的指标关注重点不同，根据不同指标选择的最优模型也不同，研究者应该根据基于copula模型解决问题的目的来选择。本研究主要关注干旱极端事件，对于模型尾部的拟合效果要求更高，因此确定Gumbel copula来模拟干旱变量之间的关系，联合概率分布见图1，函数表达式为：

C（u，v）=exp[-[（-lnu）1θ+（-lnV）1θ]θ] （13）

2.1.2 参数估计及不确定性分析 使用贝叶斯分析和MCMC模拟来寻找参数的后验分布，为了量化copula模型的不确定性，绘制了一组Copula族的后验参数分布图，见图2。图中上方的符号表示局部优化方法得到的copula函数的参数，而柱状图表示根据MCMC模拟得到的参数，横坐标上的“×”代表MCMC的最大似然参数。由图2可以看出，图中上方的符号与下方的“×”位置明显不同，表明这2种方法估算的参数有明显差异。MCMC模拟模型参数的RMSE为0.0763，而局部优化算法模拟参数的RMSE值为0.2231，在拟合度上全局优化算法相对局部优化算法有明显的优势。由图2（b）发现，Gaussian copula的参数分布接近均匀分布，这表明观测数据包含的信息不足以约束copula的参数。另外，由图2（c）发现，Tawn copula的第2个参数分布在参数的边界上得到合并，最大似然参数位于边界上，这意味着优化算法试图通过越界来提高拟合度，这是不合理的，也表明选择这样的copula对于数据的拟合不恰当。

2.2 干旱特征分析

2.2.1 干旱事件 为了比较不同时间尺度下的干旱特征，本文分别计算了时间尺度为3个月、6个月和12个月的SPI，不同时间尺度的SPI序列变化趋势基本相同，都反映了流域旱涝交替的特征。时间尺度越小，SPI随时间的波动频率越高，时间尺度越大，SPI序列越平坦。本研究选择3个月尺度的SPI，以反映农业干旱情况[9]。将干旱划分为特旱、重旱、中旱、轻旱几个等级，在流域的干旱情况中，秋冬季节在1年中干旱较为严重。在研究区内，发生了3次特旱事件，分别在1965年冬季、1965年秋季和1997年秋季;春季只在2000年发生了1次严重干旱，夏季在1968年和2001年和发生了严重干旱，其余春夏季节发生的干旱事件均集中在轻旱、中旱;秋季分别在1965年和1997年发生了特旱，在1972年和1986年发生了严重干旱;冬季在1965年发生了特旱，在1970年、1997和1998年发生了严重干旱。在研究的时间序列中，秋冬季发生干旱的频率也明显高于春夏。

2.2.2 干旱重现期 干旱事件的频率往往用重现期来表示，是水文信息的一个重要参数[15]。计算重现期，首先要建立合适的多变量的联合概率分布，然后才可以根据式（14）-（16）计算。单变量的重现期计算公式为：

T=[L1-F（x）] （14）

式中：T为重现期，F（x）为累积概率分布函数，[L]为干旱事件的平均时间间隔。

对于双变量干旱事件，在随机变量的取值范围内，各个变量同时大于某一设定的值，重现期的计算公式为：

P（T≥t∩S≥s）=1-u-v+C（u，v） （15）

Tds=[LP（T≥t∩S≥s）]=[L1-u-v+C（u，v）] （16）

式中：T、S表示干旱时间、干旱烈度，u、v代表干旱历时、干旱烈度概率分布函数

用Gumbel copula来模拟干旱历时和干旱变量之间的依赖结构，分析干旱重现期，干旱变量的重现期见图3。首先计算干旱间隔时间为13.38（月），根据式（13）～（15）计算得到，对于单变量重现期而言，研究序列中发生的最严重干旱事件的重现期（干旱历时、干旱烈度）分别为9.13年一遇、43.2年一遇。就双变量联合重现期而言，在所研究的时间序列中，发生最严重的干旱事件，同现重现期为32年一遇、而联合重现期为90年1遇。比较分析近60年里汾河上中游地区发生的几次典型干旱事件，1965年发生29年一遇的干旱事件持续了7个月，直到1966年3月旱期才开始减轻。1972年发生干旱同样连续持续了7个月，干旱程度主要为中旱，这次干旱事件严重程度相比1965年程度较轻，但旱情反复出现，在接近1年之后才结束，重现期约为26年一遇。此外，在1986年发生了持续7个月的干旱，干旱程度也均为重旱、特旱;1997年发生干旱持续了6个月的干旱事件，干旱程度几乎持续保持特旱，重现期为28年一遇。

3 结论与讨论

干旱事件的各个变量之间是密切相关的，研究它们之间的相互关系对于干旱预测和风险评估至关重要，copula函数可以很好地模拟干旱特征变量之间的关系、模拟干旱事件的发生，是干旱分析的有效工具，对于旱情的监测和预报有重要意义。本文基于汾河流域近60年的逐月降水数据，以SPI3为指标基于游程理论识别干旱事件，采用多元copula分析工具箱在贝叶斯框架下使用MCMC模拟来估计copula参数及其潜在不确定性，计算拟合copula概率的等值线，再利用Copula函数建立的联合分布分析汾河流域的干旱特征，得到的结论有：

（1）由SPI很好的反映汾河流域的多年干旱情况：在长时间序列下流域表现出旱涝交替的特点;秋冬季节的干旱明显比春夏季节严重，干季的干旱比湿季严重;且观察多年SPI的变化趋势，发现整体呈现轻微下降趋势，证明汾河流域的干旱情势并不乐观。

（2）通过干旱识别、拟合优度评价选择copula函数、估計函数参数等步骤，拟合汾河流域干旱事件历时和烈度的最优copula为参数值等于2.0461的Gumbel copula，通过干旱频率分析，汾河流域在1960—2020年内发生最严重的干旱为90年一遇;

（3）贝叶斯方法是模型参数估计的有效方法，相对于以往常用的局部优化方法具有一定的优势。在以往研究中常用的局部优化算法会存在陷入局部最优的现象，导致结果有偏差，而贝叶斯框架下的MCMC模拟，可以得到全局最优解，还能提供参数估计的潜在不确定性。尤其是数据信息有限时，copula函数参数估计存在很大的不确定性。

本研究对于干旱事件的描述仅选取了干旱历时和干旱烈度2个变量，选择的特征变量越多，在计算过程中建立多变量间的copula函数越复杂，参数估计也越难计算。因此我们还需要考虑如何提出更简单有效的方法，在基于多个特征变量的基础上降低计算的复杂性。此外，目前水文文献中常用的copula函数仅局限于固定的几个（Gaussian、t、Frank、Gumbel和Clayton），但存在的问题是这些copula函数有时不能很好的描述变量间的依赖结构。

参考文献

[1]Zhang Q， Yao Y， Li Y， et al. Causes and Changes of Drought in China： Research Progress and Prospects[J].Journal of Meteorological Research， 2020，34（3）：460-481.

[2]屈艳萍，吕娟，苏志诚，等.抗旱减灾研究综述及展望[J].水利学报，2018，49（01）：115-125.

[3]徐翔宇，许凯，杨大文，等.多变量干旱事件识别与频率计算方法[J].水科学进展，2019，30（03）：373-381.

[4]刘章君，郭生练，许新发，等.Copula函数在水文水资源中的研究进展与述评[J].水科学进展，2021，32（01）：148-159.

[5]陈文华，徐娟，李双成.怒江流域下游地区气象与水文干旱特征研究[J].北京大学学报（自然科学版），2019，55（04）：764-772.

[6]韩会明，刘喆玥，刘成林，等.基于Copula函数的赣江流域气象干旱特征分析[J].水电能源科学，2020，38（08）：9-13.

[7]龙瑞昊，畅建霞，张鸿雪，等.基于Copula的澜沧江流域气象干旱风险分析[J].北京师范大学学报（自然科学版），2020，56（02）：265-274.

[8]覃丽华，张鑫.基于连续干旱游程的干旱特征分析与应用[J].中国农村水利水电，2020（10）：164-169.

[9]赵雪花，赵茹欣.水文干旱指数在汾河上游的适用性分析[J].水科学进展，2016，27（04）：512-519.

[10]王鹏新，冯明悦，孙辉涛，等.基于主成分分析和Copula函数的干旱影响评估研究[J].农业机械学报，2016，47（09）：334-340.

[11]Prakash A，Panchang V，Ding Y，et al. Sign Constrained Bayesian Inference for Nonstationary Models of Extreme Events[J]. Journal of Waterway Port Coastal and Ocean Engineering， 2020， 146（5）：04020029.

[12]Gupta V，Jain M K，Singh V P. Multivariate Modeling of Projected Drought Frequency and Hazard over India[J]. Journal of Hydrologic Engineering，2020，25（4）：04020003-1-19.

[13]Sadegh M，Ragno E，Aghakouchak A. Multivariate Copula Analysis Toolbox （MvCAT）：Describing dependence and underlying uncertainty using a Bayesian framework[J]. Water Resources Research，2017，53.

[14]Zhu S，Luo X，Chen S，et al. Improved Hidden Markov Model Incorporated with Copula for Probabilistic Seasonal Drought Forecasting[J]. Journal of Hydrologic Engineering，2020，25（6）：04020019.

[15]周平，周玉良，金菊良，等.水文雙变量重现期分析及在干旱中应用[J].水科学进展，2019，30（03）：382-391.

（责编：王慧晴）