振动台模型试验相似理论分析
2021-09-14郭明珠孙海龙
郭明珠,邹 玉,孙海龙
(北京工业大学城市建设学部,北京 100124)
在2020年发布的“十四五规划和二〇三五年远景目标的建议”中,川藏铁路重大工程成为我国未来西部工程建设重点之一。铁路建设沿线途中经过许多高山峡谷河流,面临众多地质灾害。滑坡在工程建设中的影响不可忽视,已成为研究热点讨论。
振动台作为研究边坡动力响应的手段之一,能够较为真实地模拟边坡在地震作用下的破坏过程和动力特性[1-3]。实际中,直接了解原型的响应机制需要耗费大量的人力物力,且原型响应机制的出现具有偶然性,依托振动台试验,通过相似理论分析,让模型更大限度的反应原型的特点,了解和分析原型的动力特性和破坏响应机制。但在传统的振动台相似设计中,参与振动台试验的各物理量的权重不能很好区分,导致材料配比试验中工作量较大;在地震波的输入上选用实际时长的地震波,不符合相似设计,会对振动台试验中破坏过程和动力特性造成影响[4-5]。
笔者以西藏自治区昌都地区芒康县索多西乡贡扎滑坡为例,详细介绍贡扎滑坡振动台模型的相似设计方法;采用量纲分析法,通过分离相似设计确定了各物理量的权重,对输入的地震波采用重力相似理论进行分析和处理,为顺利开展振动台试验打下基础。
1 相似理论
模型和原型的几何学、动力学和运动学都相似,认为原型和模型真正相似。相似的背后是现象中多个物理量之间存在某种特定的表达形式,它们不是孤立存在的而是相互联系的。几何相似是指原型的尺寸(长宽高)按一定比例缩小成模型。动力学相似是指作用在模型和原型上的力相似,在振动台试验中主要强调重力相似[6]。运动学相似是指模型中产生运动的点,与原型中对应点的情况相似,即模型中运动点的速度、加速度和运动时间与原型中的点对应成比例,且速度和加速度对应的方向相同[7]。
在模型试验中,实现几何相似容易。在保证模型和原型的形状相同的同时,保证对应角度相等,对应长度成比例。
在满足几何相似的前提下,实现动力学相似,则模型的运动学也应相似。在三种相似中,动力学相似最为重要。相似理论的基础是相似三定律,是从相似现象的物理方程出发,总结出的三条公认的结论。相似三定律在模型试验中具有很好的指导作用,对复杂的原型进行理论分析,建立相对简单的模型来反映事物本质[8]。
1.1 相似第一定理
相似第一定理是指两个物体所表现的现象相似,则规定其相似指标为1。第一定理是现象相似的必要条件,揭示了两个相似的现象在数量和空间的相互关系[9],下面用牛顿第二定理来解释。
牛顿第二定理:
(1)
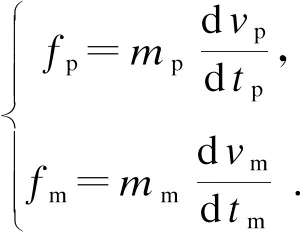
(2)
式中:下标p、m分别表示原型(prototype)和模型(model)物理量。
因模型和原型运动现象相似,可由式(2)推出:
(3)
式中:Cv、Ct、Cm、Cf分别为速度、时间、质量和力的相似比。
将式(3)带入式(2)中,可得:
(4)
通过式(2)、(4)可知,必定存在
(5)
或

(6)
式中:Ci为相似比,即在两个彼此相似的运动现象中,其相似指标为1。由式(6)可知,原型和模型中的各物理量的相似比必须受到“相似指标为1”的严格限制。
1.2 相似第二定理(π定理)
相似第二定理是白金汉在1914年所提出,是现象相似的必要条件。
π定理的定义如下,某一物理现象中存在n个物理量,即β1,…,βk,…,βn,物理量之间存在着如下的完整关系:
φ(β1,…,βk,…,βn)=0.
(7)
或
β=f(β1,…,βk,…,βn) .
(8)
如果上式中n个物理量中有k个基本物理量(β1,β2,…,βk)的量纲是相互独立的,则通过单位尺度的变换,就可将上述关系式化为无量纲π方程,即:
π=f(1,1,…,π1,π2,…,πn-k).
(9)
式中:π1,π2,…,πn-k是由β1,β2,…,βk中k个量纲独立的物理量所组成的无量纲参数。
1.3 相似第三定理
相似第三定理是指模型和原型的现象表现出同一特征。如果单值条件相似,由单值条件的物理量所组成的相似准则在数值上相等,则认为物理现象一定相似。单值条件是物理现象相似的充要条件[10],是指从多个物理现象中把某个具体现象挑选出来的条件。单值条件可概述为以下四个:几何条件、物理条件、边界条件和初始条件。
(1)几何条件是指现象中的几何尺寸给出的单值条件。
(2)物理条件是指现象均是由物质所引起的,且每种物质具备相应的物理性质,参与现象的物理性质需给出单值条件,如密度,泊松比。
(3)边界条件是指周边环境的存在会对现象产生作用,在考虑边界的影响下,对边界的情况也应给出单值条件,如约束条件,底部摩擦。
(4)初始条件是指现象的初始状态会影响发展过程,初始状态也应给出单值条件,如初速度、岩体结构特征。
在相似分析中以相似理论为基础,满足相似三定律是可行的,但在现实模型试验中,很难达到所有相似条件都满足。为了更好地进行模型试验,减轻相似设计工作量,在相似设计中普遍采用量纲分析法。
2 量纲分析法
2.1 由量纲分析法导出的相似关系
两个相似现象之间的关系可以通过量纲分析法来建立。当一个现象可以用某物理方程来表达,即也能用量纲方程来表达。但要解决不能用物理方程来表达的某些现象,量纲方程的出现就起到很大作用。量纲分析法的重大作用在于通过π定理减少了问题中物理量的个数,减轻了任务量,便于很快了解未知的复杂现象,这对试验安排有着难以估量的重要性。
根据传统的量纲分析法,建立原型和模型的静力相似物理关系。在模型试验过程中,与岩质边坡有关的参数分别是:高度L、材料密度ρ、重力加速度g、黏聚力c、内摩擦角φ、弹性模量E、剪切模量G、应力σ、剪应力τ、应变ε;与输入地震波有关的参数分别是:持时t、加速度时程幅值a、频率ω。
f(L,ρ,g,c,φ,E,G,σ,τ,ε,t,a,ω)=0.
(10)
以质量M、长度L及时间T作为基本量纲的MLT量纲系统,其他物理量量纲可由MLT表示,即:
ρ=ML-3.
(11)
g=LT-2.
(12)
c=ML-1T-2.
(13)
E=G=ML-1T-2.
(14)
σ=τ=ML-1T-2.
(15)
a=LT-2.
(16)
φ=ε=1
(17)
ω=T-1.
(18)
在以MLT的基本量纲的系统中,要选定多个物理量作为控制量。首先需要考虑模型与原型之间的尺寸,试验装置为北京工业大学抗震与结构诊治试验室振动台,该振动台台面长3 m,宽3 m。通过振动台的尺寸大小,确定模型箱的尺寸为长2.7 m,宽1.1 m,高1.5 m的钢结构模型箱,如图1所示。

图1 振动台模型箱
试验以贡扎滑坡为原型,滑坡体高度270 m,滑坡后缘高程3 320 m,前缘高程2 600 m,倾角为55~70°,倾向N30°E。滑坡后缘最高点至左岸冲击区最高点总长度为1 802 m,左右边界最大宽度725 m,如图2所示。

图2 边坡原型图
通过滑坡剖面图模型箱尺寸确定原型和模型的几何相似比为CL=1 000,如图3所示。

图3 贡扎滑坡剖面图
在模型试验中,边坡的自重荷载无法由施加外力来实现,需要材料自重来满足,因此取原型与模型的密度相似比为Cρ=1。模型、原型处于同一个重力场作用下,则重力加速度相似比为Cg=1。基于上述分析,选取L、ρ、g作为其他参数的相似判据。
由式(8)改写成无量纲方程,则任意无量纲项可以表示为[11]
π=Lα1ρα2gα3cα4φα5Eα6Gα7σα8τα9εα10aα11·tα12ωα13.
(19)
式中:α1~α13为各物理量的因次。将式 (11)~式(18)带入式(19)中可得其余物理量的相互关系,如式(20)~式(27)所示。
(20)
(21)
(22)
(23)
(24)
(25)
(26)
(27)
令无量纲的相似比为1,即Cφ=Cg=1,则由相似判据可得其他物理量与三个基本物理量的相似关系,如式(28)~(35)所示。
(28)
(29)
(30)
(31)
(32)
(33)
(34)
(35)
基于π定理和量纲分析法确定的量纲和相似系数表如表1所示。

表1 量纲和相似系数表
2.2 由分离相似设计导出的相似关系
在上述静力相似设计中,通过量纲分析法进行相似分析,所有的物理参数由一个特征方程所表示,无法显示各物理量的权重比例。利用分离相似设计对量纲分析法进行优化,在多级特征方程中对所有参数进行筛选,从而确定关键参数、相关参数和无关参数。在试验材料配比上,必须率先满足关键参数相似,对相关参数进行调整。
采用王志佳[12]提出的分离特征方程法,根据边坡和地震波的物理量,进行相似设计。将边坡控制参数L、ρ、g作为控制量,得出一级特征方程:
f(L,ρ,g|c,φ,E,G,σ,τ,ε,t,a,ω)=0.
(36)
通过分离特征方程,得出边坡和地震波的二级特征方程:
(37)
(38)
由二级特征方程推导出的相似常数表如表2、表3所示。
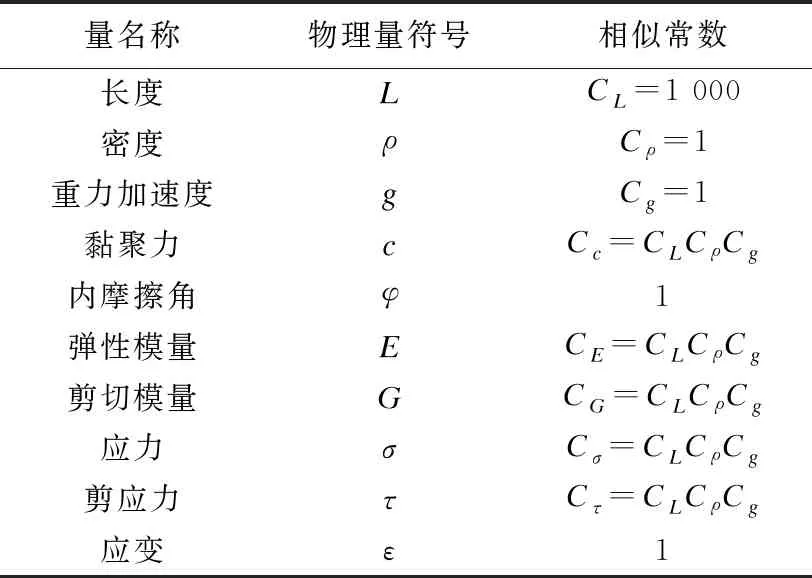
表2 模型边坡的相似常数表

表3 地震波的相似常数表
在地震波的二级特征方程,式(38)中,由边坡控制参数L、ρ、g作为推导地震波方程中待确定参数的控制参数,对于地震波本身没有实际意义。
为更好地了解控制模型和原型的关键参数,可以发现在边坡模型振动台试验中,通常采用土和其他材料混合制成的土坯来模拟边坡。岩土体的破坏准则为摩尔库伦准则τ=c+σtanφ,则影响模型破坏的关键参数为τ、c、σ、φ。通过再次分离特征方程,可以得出边坡的三级特征方程为
(39)
参数G、ε为相关参数,由三级特征方程推导出的关键参数相似常数如表4所示。
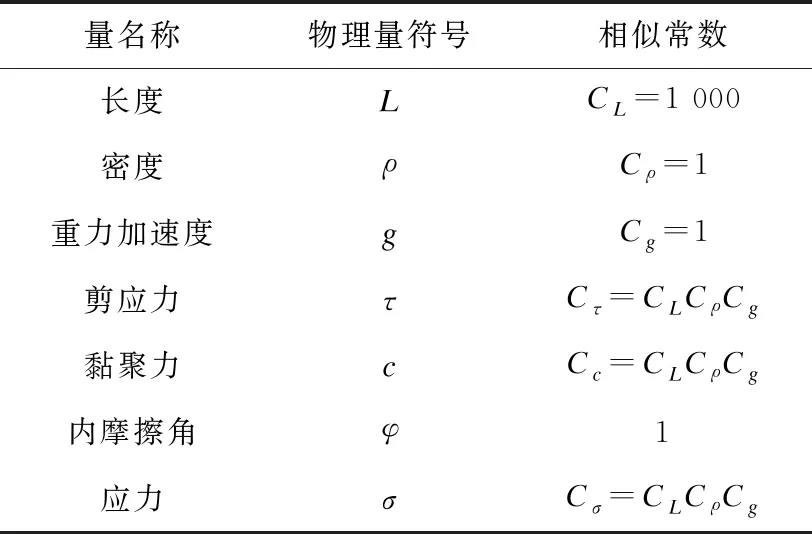
表4 关键参数相似常数表
通过4个特征方程,确定各物理量在模型试验中的权重,并依此划分为控制参数、关键参数、相关参数和无关参数。在以L、ρ、g作为控制参数的相似设计中,关键参数直接反映模型的动力响应特性,在试验始终都应严格保证关键参数的相似,物理参数权重划分如表5所示。

表5 物理参数权重划分
3 重力相似律
在弹性结构体系中,振动方程如下:
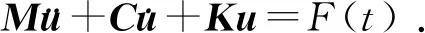
(40)
式中:M、C、K分别为结构的质量矩阵、阻尼矩阵和刚度矩阵。
从岩石大变形来看,土石混合料连续弹性体的性质不明显。在边坡振动台试验中,随着输入加速度的增大,土石混合料的强非线性愈发显著,进而需放弃弹性恢复力相似,保持惯性力和重力相似。
在分离相似设计中,通过边坡参数L、ρ、g作为推导地震波的控制量,无法很好地反应模型边坡在地震作用下的响应特征。振动体系中,由于惯性力、重力和弹性力的作用,土石混合物不能作为纯粹的弹性体。在相似设计中,只需考虑惯性力和重力对振动的影响,保持重力相似,不考虑弹性恢复力相似。在动力相似中,对输入地震波进行相似设计[13-14],能够真实地模拟边坡在地震波作用下的响应特性。
在重力作用下,边坡原型和模型的重力相似关系式为
(41)
在惯性力作用下,边坡原型和模型的惯性力相似关系式为
(42)
在动力相似中,只考虑重力和惯性力的影响,保持动力相似,即
(43)
在动力相似中,所有作用力的比例系数都应保持一致,同时满足重力与惯性力相等,则由式(37)、(38)、(39)可得相似关系表达式:
(44)
简化后相似指标:
(45)
在振动台试验中,输入的地震波需要按时间相似比Ct=32进行压缩[15-16],可模拟出原型边坡在地震波作用下的响应特性。
4 结 论
(1)传统的量纲分析法无法确定各物理量的重要程度,对下一步进行的材料配比试验造成很大的工作量;采用分离相似设计解决了各物理量权重的问题,在相似配比试验中可优先满足控制量L、ρ、g和关键参数τ,c,φ,σ相似下,进而满足相关参数G,ε相似,在一定程度上减轻了相似材料配比时的工作量。
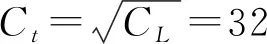
(3)根据相似三定律、量纲分析法、分离相似设计和重力相似理论,确定了贡扎滑坡振动台模型的相似设计及各物理量相似比:CL=1 000、Cρ=1、Cg=1、Ct=32、Cc=1 000、Cφ=1、Cσ=Cτ=1 000、CG=1 000、Cε=1,同时为相似的振动台模型试验提供一定参考。
