基于基本参数法的EDXRF全谱拟合定量算法及其应用

刘明博， 廖学亮， 程大伟， 倪子月， 王海舟*

1. 钢铁研究总院， 北京 100081 2. 钢研纳克检测技术股份有限公司， 北京 100081

引 言

X射线荧光(XRF)方法定量测试的依据是元素特征线强度与其在样品中的含量成正比， 但如果样品中某个元素含量较高， 并且其特征线能量高于其他共存元素的吸收限， 就会对其他元素形成二次激发， 从而导致其特征线强度被提高， 而自身的特征线强度被降低， 这就是吸收增强效应。 吸收增强效应的存在扰乱了元素特征线强度与含量的正比例关系， 对XRF定量测试造成困扰。 此外， 由于每个元素都会有不止一条谱线， 且能量各不相同， 而元素对不同能量的吸收有差别， 这会导致混合样品中元素多条谱线的相对强度发生变化。

在进行能量色散X射线荧光(EDXRF)分析的解谱操作时， 如果各元素谱线重叠不严重， 用最优化算法进行谱线拟合[2]就可以得到较为精确的谱峰强度， 谱线重叠严重时， 仅靠最优化计算则无法得到各个谱峰的准确强度， 对于这种情况的处理可分为两种情况， 如果该样品中各元素含量不高， 相互间吸收增强效应不明显， 此时用纯元素谱剥离的方法会有较好的效果[3]， 而当样品中元素含量较高时， 如前所述， 相互间较强的吸收增强效应会导致元素多条谱线的相对高度与纯物质时不一致， 用纯物质的谱图为依据进行剥离解谱， 就会导致谱线强度的失真。

图1是高浓度La/Ce/Pr/Nd稀土混合溶液样品的实测谱图及其与纯元素谱拟合解谱的对比[1]， 由于吸收增强效应的存在， 采用固定的纯元素谱做最优化计算， 在Pr:La、 Nd:La、 Nd:Lb1、 320道、 335道和348道附近， 拟合谱图与实测谱有明显偏差， 用这种方法拟合解谱得到的结果也就无法反映实际的谱峰强度， 以此为依据计算的含量结果也就不会准确。

图1 La/Ce/Pr/Nd混合液样品实测谱图与纯元素谱拟合的对比Fig.1 Comparation of origin spectrum andoptimized by pure spectrums

在EDXRF定量计算中， 基本参数法(fundamental parameters,FP)能够以光管靶材、 激发电压、 出射角、 滤片材质厚度、 光路尺寸、 样品构成、 探测器响应效率、 分辨率等参数为基础[3]， 采用Sherman方程， 通过一步步的计算得到理论谱图[4]。 基本参数法可以通过一次、 二次荧光的计算充分考虑吸收增强效应对谱线的影响， 因此将其应用于EDXRF的纯元素解谱过程中会有比较不错的效果。

为了解决高浓度情形下复杂样品体系的EDXRF解谱问题， 本文介绍一种基于基本参数法(FP)的全谱拟合定量算法， 该方法以纯元素谱图拟合为基础， 结合FP计算， 在进行EDXRF谱图解析的同时， 完成定量计算。

1 算法原理

基于基本参数法的纯元素谱图扣除算法原理如图2所示， 其所涉及的各个流程说明如下：

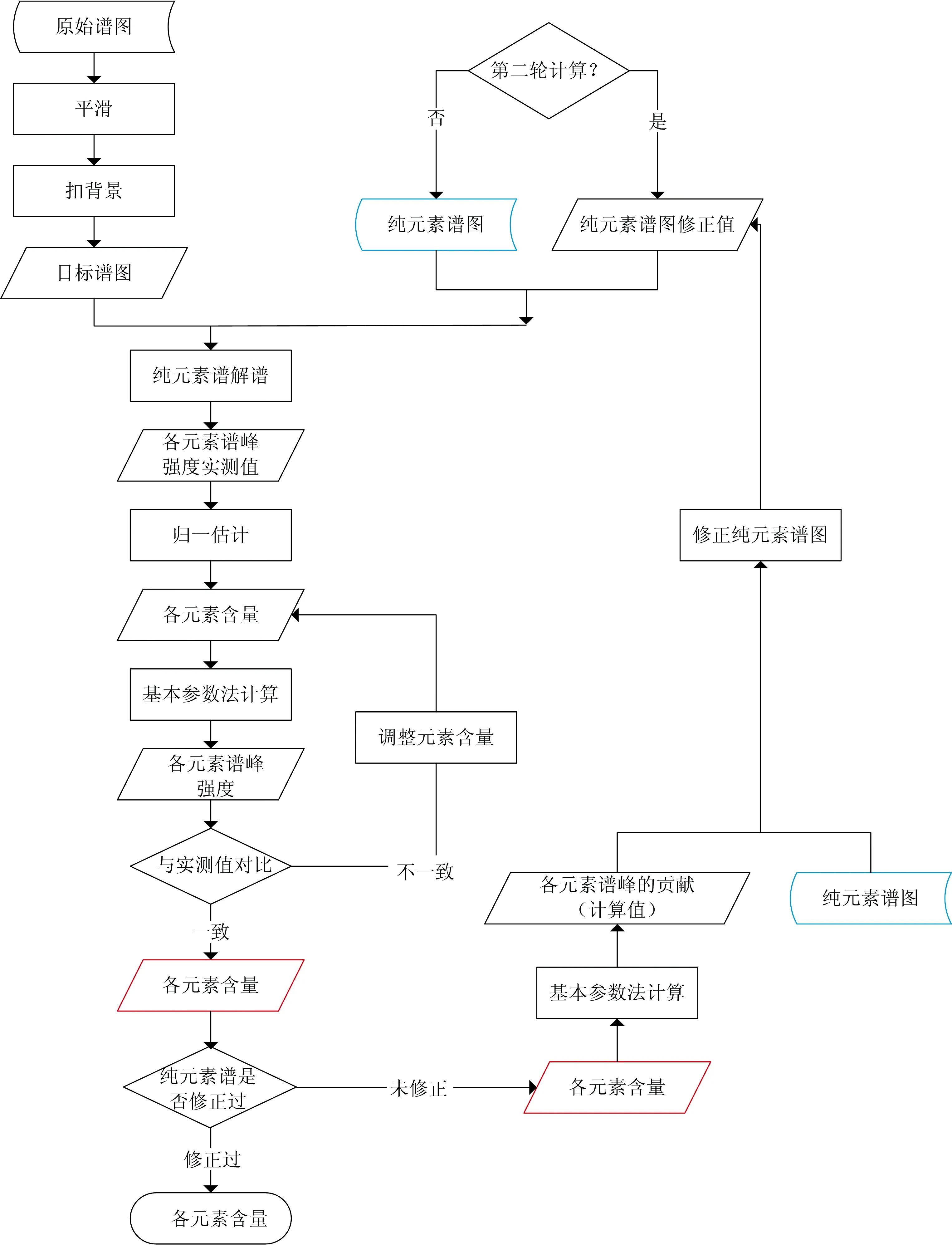
图2 算法流程图Fig.2 Flowchart of algorithm

(1) 采集待测样品的原始谱图， 并做平滑和背景扣除， 作为后续处理的目标谱图；

(2) 第一轮计算开始， 采集相同条件下各待测元素的纯物质谱图；

(3) 采用“最优化算法与纯元素谱剥离相结合的EDXRF解谱方法”， 用纯元素谱图拟合目标谱图， 得到各元素谱峰强度的实测值；

(4) 以各元素主峰强度为依据预估该元素含量， 例如用强度归一的方法做预估， 得到样品中各元素的含量；

(5) 以预估的元素构成做基本参数法计算， 可以得到各元素的计算谱峰强度， 然后与实测值比较， 依据一定的策略调整预估的元素含量， 重复迭代， 直至各元素的计算峰强与实测值无差别， 至此就初步得到元素含量；

(6) 以初步得到的各元素含量为依据， 用基本参数法计算各元素对目标谱图的实际贡献， 再用该部分谱图的形状修正原始纯元素谱， 得到纯元素谱图修正值；

(7) 此后的操作称为第二轮计算， 用纯元素谱图的修正值替换纯元素谱图， 重复步骤3—步骤5会再次得到各元素含量， 并将其作为最终的定量结果。

2 计算实例

为了验证本文介绍的基于基本参数法的纯元素谱图扣除算法， 依然采用前面提到的高浓度La/Ce/Pr/Nd稀土混合溶液样品， 首先执行算法步骤1—步骤6， 该过程使用的是原始的纯元素谱图， 谱图拟合结果如图1所示， 可以看到多处明显的偏差， 拟合谱图与实测谱的残差σ为1 415.0。 步骤6之后会得到修正的纯元素谱图， 各元素的原始纯元素谱图与修正纯元素谱图的对比如图3所示。

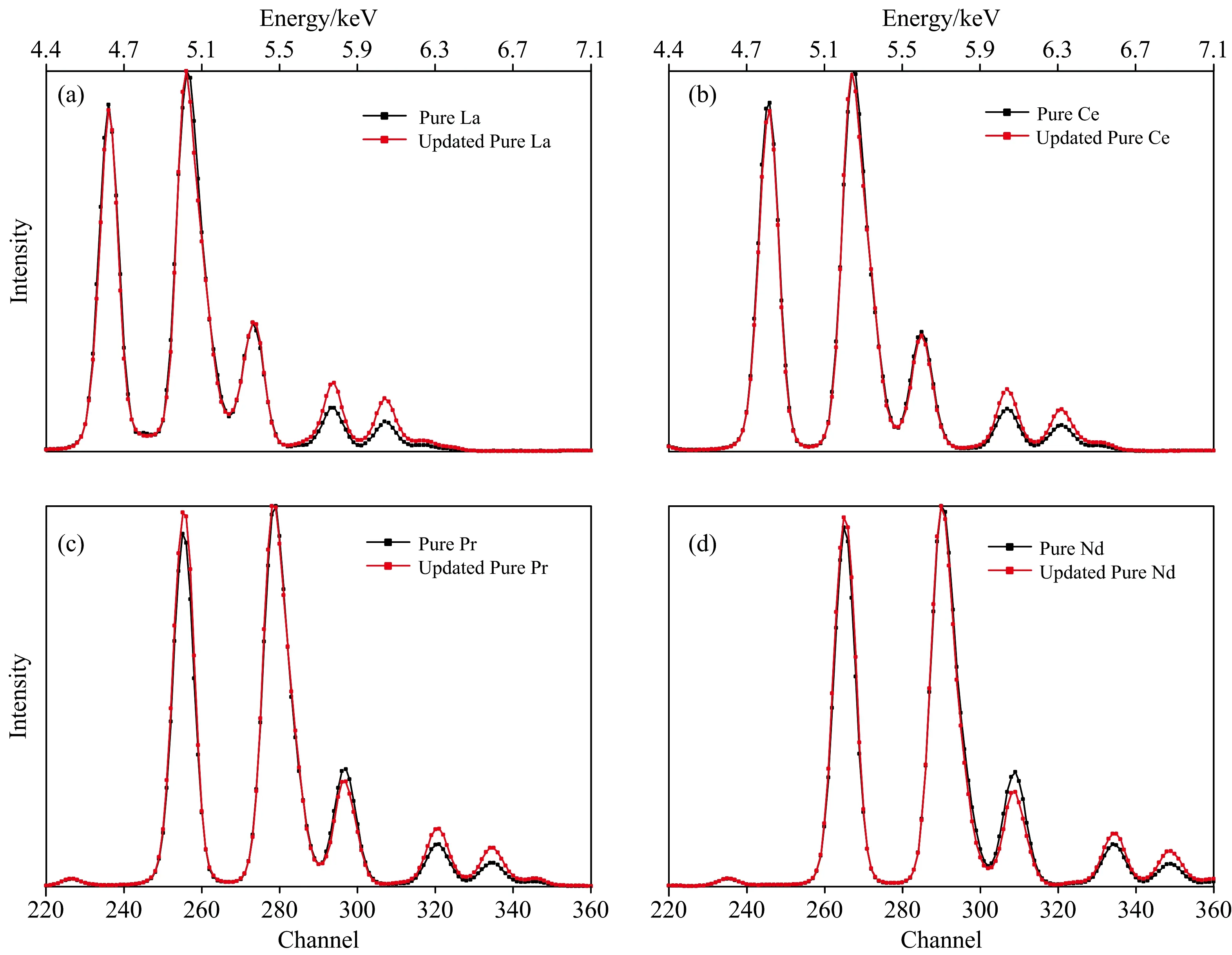
图3 纯元素谱图形状修正前后对比Fig.3 Comparation of pure spectrum and its updated

从图3的对比可见， 由于样品中各元素浓度较高， 相互之间存在较强的吸收增强效应， 并且La， Ce， Pr和Nd四个元素的L系谱线较复杂， 因此导致混合样品中的谱线改变程度各有不同。

以如上修正后的纯元素谱图按照算法步骤7执行， 就会得到与原始谱图更为吻合的谱图拟合结果(新方法计算得到的谱图与实测谱的残差σ降至474.5)， 如图4所示， 同时还会得到较为准确的含量结果， 如表1样品STD所示。 用该方法又对生产线上取出的另外6份稀土混合液样品进行了测试， 并与ICP方法的测试结果进行了比对， 各样品各元素配分含量偏差均小于1%。

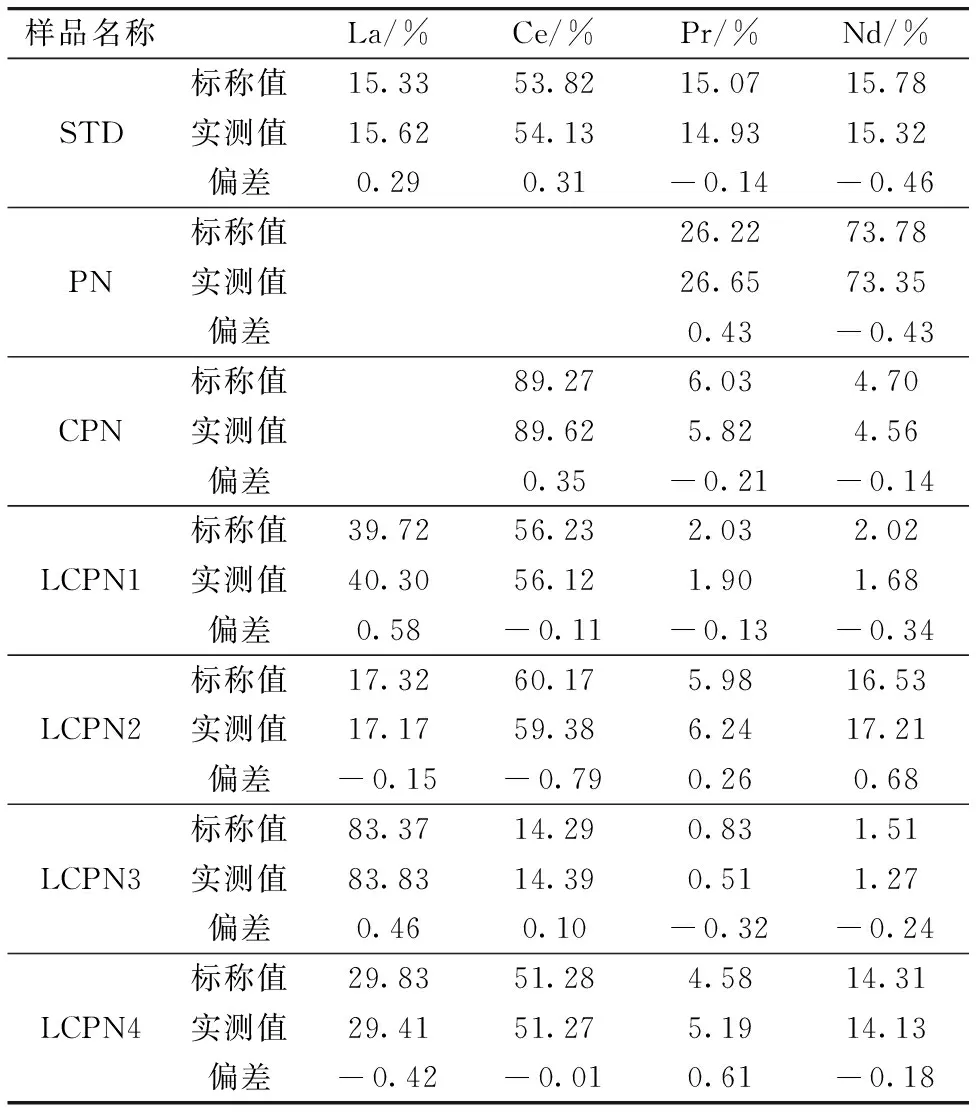
表1 实测配分结果与标称值的对比Table 1 Tested results and certified

图4 La/Ce/Pr/Nd混合液样品实测谱图与 修正后纯元素谱拟合的对比Fig.4 Comparation of origin spectrum and optimizedby updated pure spectrums

用该方法对上述样品做连续11次测试， 结果如表2所示， 可见各元素配分含量的相对标准偏差均小于1%， 极差小于0.6%， 各元素结果与标称值的偏差小于生产控制要求的偏差小于1%的指标。 依据该方法开发的XOR-50型稀土配分在线分析仪已经很好地服务于稀土冶炼行业[5]。

表2 实测配分稳定性Table 2 Tested results of stability

3 结 论

基于基本参数法的EDXRF全谱拟合定量算法将基本参数法的计算和纯元素谱图扣除算法相结合， 修正了吸收增强效应对纯元素谱图形状的影响， 从而使得解谱精度更高， 同时在方法的运行过程中通过FP迭代得到了精确的含量结果， 是一种比较完善的常量元素EDXRF定量和解谱方法。

通过对高浓度La/Ce/Pr/Nd混合溶液样品的解析， 得到了比较准确的谱图拟合与浓度定量结果， 与标准方法相比测试各元素偏差均小于1%， 且方法稳定性较好， 以此方法为依据开发的XOR-50型稀土配分在线分析仪， 连续11次测试RSD<1%， 能很好地服务于生产实践。