考虑电转气响应特性与风电出力不确定性的电-气综合能源系统协调调度

高 晗，李正烁

（1. 山东大学 电气工程学院，山东 济南 250061；2. 山东大学 电网智能化调度与控制教育部重点实验室，山东 济南 250061）

0 引言

截至2020 年底，我国可再生能源装机总量达9.34×108kW，其中风电装机2.81×108kW，光伏装机2.53×108kW。当年弃风、弃光量分别为1.66×1010、5.26×109kW·h时［1］，弃风、弃光现象突出。此外，为了实现碳达峰、碳中和的目标，我国提出构建以新能源为主体的新型电力系统［2］，未来风、光等可再生能源装机占比将进一步提升，煤电机组等可调节资源占比将进一步降低，电力系统风光消纳能力面临严峻挑战。燃气机组运行效率高、具备快速调节能力，可以有效应对风电波动，因而得到快速发展；此外，电转气P2G（Power-to-Gas）设备可以将多余的电能转换为天然气，实现可再生能源消纳与能量的大规模存储运输［3］，国内外展开了一系列试点工程［4］；随着P2G设备与燃气机组的部署，电力、天然气系统实现紧密耦合。研究电力、天然气系统的协调调度对构建以新能源为主体的新型电力系统，实现碳达峰、碳中和目标具有重要意义。

传统优化调度中，天然气系统和电力系统相互独立，缺少数据和指令的交互［5］。随着系统间耦合关系加强，实现系统间信息共享和协调调度有利于提升能源利用率和系统运行经济性、安全性。为充分发挥多能互补的优势，国内外学者围绕电-气综合能源系统的协调调度开展了广泛研究。文献［6］基于混合整数线性规划，建立了电-气综合能源系统的最优能量流模型；文献［7］以天然气输气量为权重，利用最短路径原理评估天然气管道等效损耗，进而提出了电-气综合能源系统的静态等效模型；文献［8］考虑电力系统和天然气系统的网络耦合约束，研究了电-气综合能源系统的协调调度问题。但上述文献主要研究了确定性调度问题，没有考虑风电等可再生能源出力不确定性。文献［9-11］进一步考虑了风电出力不确定性，文献［9］考虑了电力系统与天然气系统间耦合关系，提出了一种联合市场模型，并设计了日前出清框架；文献［10］利用蒙特卡洛模拟生成各种风电预测场景，研究了风电不确定条件下的电-气综合能源系统协调调度；文献［11］建立了风电出力不确定性条件下的鲁棒调度模型，并在研究中考虑了P2G 设备。但是，文献［11］直接采用了简单的无时延P2G 模型，忽略了P2G 设备响应特性。实际上，P2G 设备包含电解制氢和甲烷化两部分，涉及复杂的物理化学过程［3］，设备运行受到爬坡速率与停启时间约束，具有响应延时［12］，上述简单模型难以保证调度结果的可行性、有效性。因此，需要进一步研究如何在电-气综合能源系统调度过程中考虑P2G 设备响应特性，建立P2G 设备精确模型，以保证系统的安全、经济运行。

本文在国内外研究基础之上建立了考虑P2G设备响应特性以及风电不确定性的电-气综合能源系统协调优化模型。利用机会约束刻画计及风电实际可用出力不确定性的系统安全运行要求，引入通用分布VPD（Versatile Probability Distribution）［13］描述风电预测误差，进而将含有随机变量的机会约束转化为采用解析形式的确定性约束；采用分段线性化PWL（PieceWise Linearization）方法，将原问题转换为混合整数线性规划问题。通过24 节点电力系统与24 管道天然气系统构成的综合能源系统验证了所提模型的有效性。与已有研究相比，本文在确定性调度问题［14］与不考虑响应特性的简单P2G 模型［15］的研究基础上，进一步研究了风电出力不确定条件下考虑响应特性的P2G 设备对电-气综合能源系统优化运行的影响。

1 考虑风电不确定性及P2G 设备的电-气综合能源系统调度模型

电-气综合能源系统由天然气系统、电力系统以及P2G设备构成。本文首先建立了电力系统及天然气系统模型，然后建立了P2G设备模型，最后建立了含P2G的电-气综合能源系统优化调度模型。

1.1 电力系统模型

电力系统主要由输电线路、发电机组以及用电负荷组成。本文采用直流潮流建立其数学模型，利用机会约束刻画风电出力不确定条件下的系统安全运行要求，电力系统模型介绍如下。

1）直流潮流模型。

式（1）为电力系统功率平衡方程；式（2）—（4）为机组出力约束；式（5）、（6）为机组爬坡约束；式（7）为线路传输容量约束；式（8）、（9）分别为煤电机组能耗成本和燃气机组耗气量函数，近似为线性函数［16］。

2）机会约束。

风电出力具有不确定性，无法准确预测。为保证系统运行安全，机组要留有一定的旋转备用，以应对风电出力被高估的情况，其表达式如下：

式（10）为t时刻机组m所能提供的旋转备用范围约束；式（11）为风电机组最大出力的机会约束，以保证系统运行在安全区间内。

1.2 天然气系统模型

天然气系统主要由天然气管道、压缩机、气源、气负荷等组成，其数学模型介绍如下。

1）天然气管道模型。

天然气管道流量与其两端节点气压以及管道长度、直径、粗糙程度等自身特性相关［17］，本文采用Weymouth 方程描述管道流量与节点气压关系，具体如下：

2）压缩机模型。

天然气在传输过程中与管道摩擦产生压力损失。因此，需增设压缩机，提升管道气压，补偿压力损失。压缩机消耗能量与压缩天然气流量近似成正比［14］，由流入压缩机的天然气提供。压缩机模型如下：

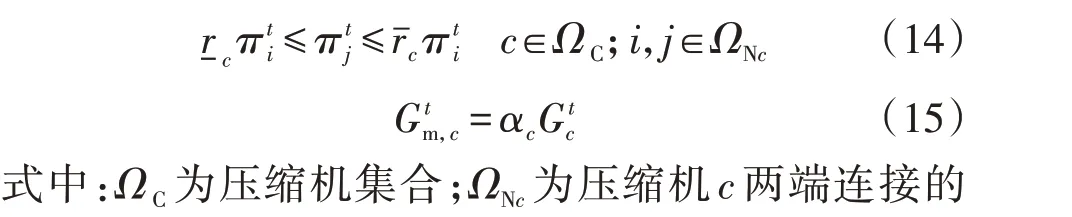
式（14）为压缩机的压缩比约束，表示压缩机两端的气压关系；式（15）为压缩机的能耗表达式，由于压缩机可以改变气体压力，其两端气压与流量关系不受Weymouth 方程式（12）约束，仅考虑能耗方程式（15）。

3）节点流量平衡。

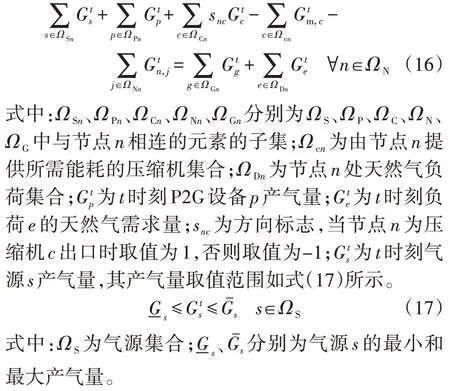
1.3 P2G设备运行模型

P2G 技术包括电解制氢和甲烷化2 个过程，其流程如图1所示。

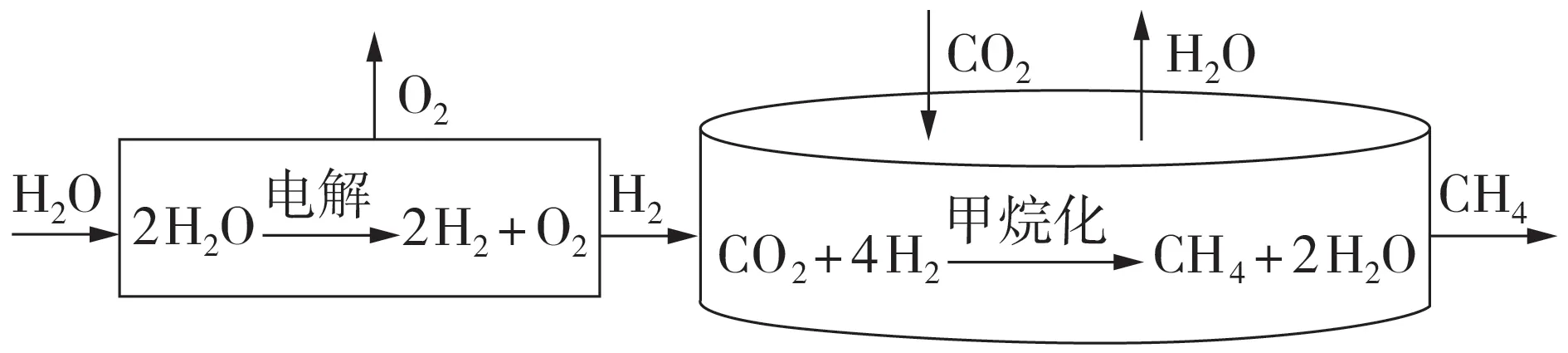
图1 P2G技术流程图Fig.1 Flowchart of P2G technology

1）响应特性。

目前，电解技术已经可以在数分钟内实现停启［18］，但甲烷化反应停启仍需数小时［3］，因此P2G 设备存在明显响应延时，需考虑设备停启时间约束。类似火电机组，P2G 设备需要一定爬坡时间来响应功率变化，但针对运行范围内的任意功率变化，P2G设备通常可在10 min 内完成响应［19］，故此处忽略其爬坡速率约束。考虑响应特性的P2G设备数学模型如下：

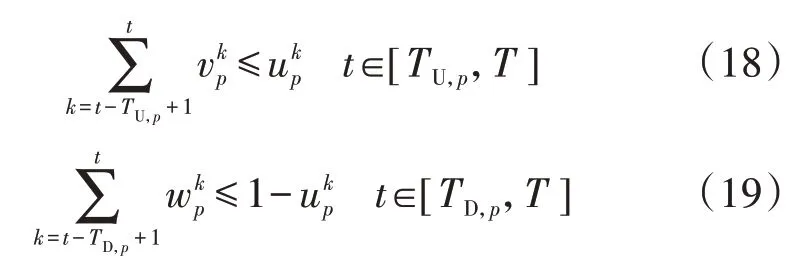
式（18）、（19）分别为P2G 设备运行时间约束和停机时间约束；式（20）为不同状态间关联约束；式（21）为P2G设备运行范围。

2）耦合关系。

P2G 设备利用电解水和甲烷化反应，将多余电能转换为天然气进行存储、运输，实现电力与天然气系统的耦合。目前电解制氢效率可达60%，甲烷化效率约为81.8%，综合能效可达50%［20］，天然气产出与所耗电能耦合关系如下：

式中：ηp为P2G设备p的能量转换系数。

1.4 目标函数

本文目标函数为最小化运行成本以及风电惩罚成本，其表达式如下：

2 求解方法

上述模型为非凸的随机规划问题，机会约束式（11）中存在随机变量难以直接求解，非凸非线性的天然气管道流量方程式（12）进一步增加了模型的复杂程度。相比于高斯分布和贝塔分布等经典理论分布，VPD可以更好地拟合风电预测误差，在不同时间尺度与置信度下，VPD 分布均能较好地拟合实际风电分布，提升了调度决策的准确性，且根据VPD 的分布函数可直接得出其分布函数逆函数的解析形式［13］，因此VPD 被广泛应用于刻画风电出力的不确定性。为了解决上述问题，本文引入VPD，其概率密度函数f(x)与分布函数F(x)表达式分别如下：

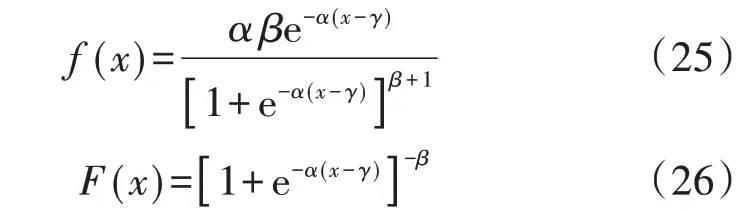
式中：x为随机变量；α、β、γ为分布函数的形状参数，可由历史数据拟合得到［15］。

VPD 分布拟合及数据处理流程如附录A 表A1所示。分布函数的逆函数如下：

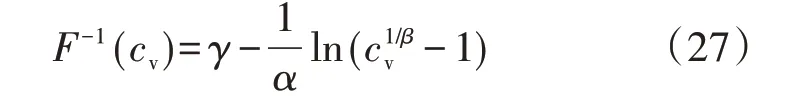
式中：cv为置信度。

基于VPD，将式（11）转化为确定性约束，过程如下：

然后，进一步利用PWL 将式（29）线性化，根据管道流量范围选取N1个离散点，得到表达式如下：

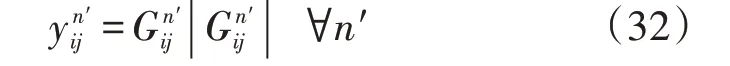
针对目标函数中的风电惩罚成本，采用数值积分方法，将其转换为线性函数，具体过程如下：

化简后的模型为混合整数线性规划模型，可直接用商业求解器求解，模型整体求解流程如图2所示。

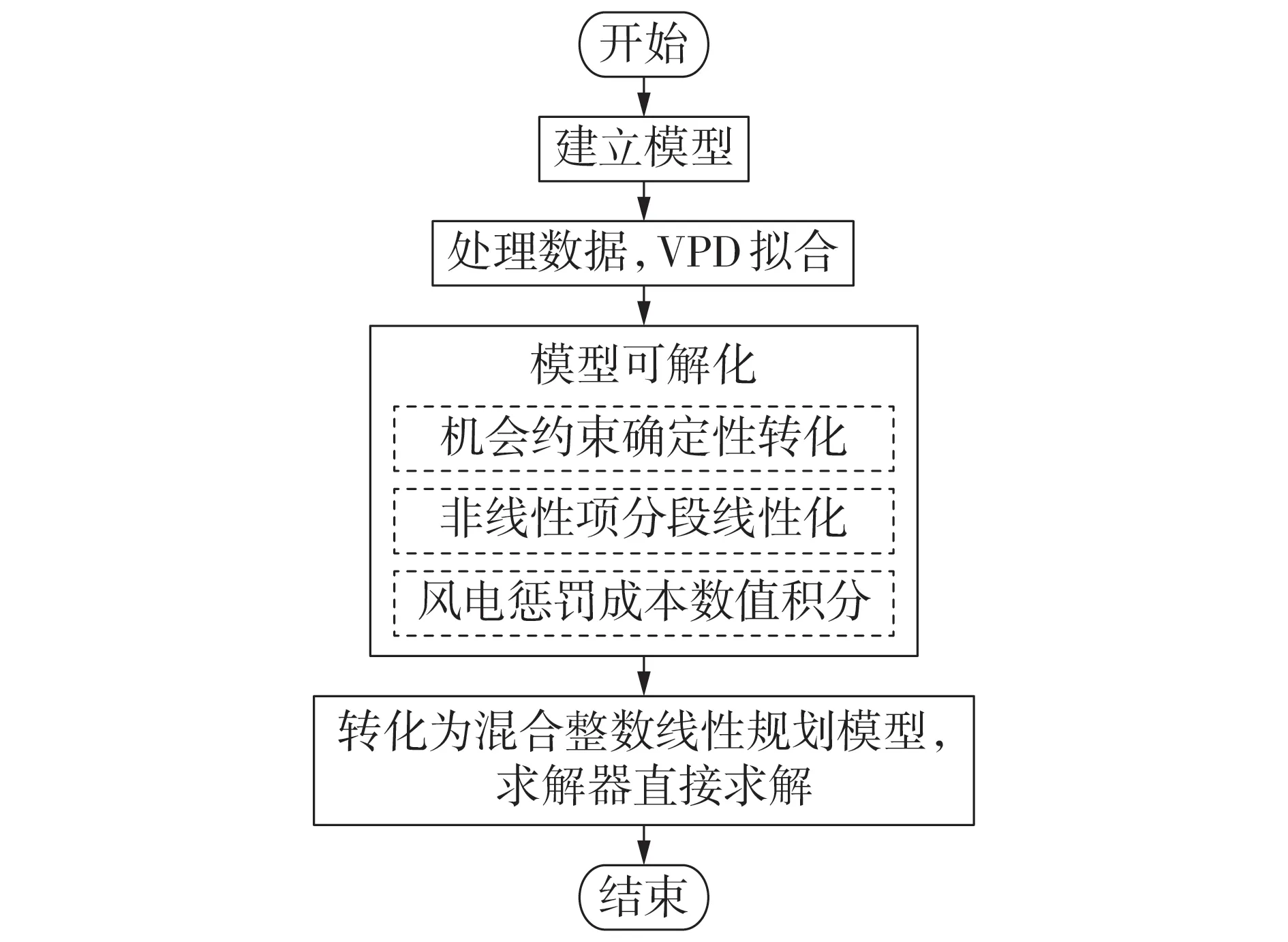
图2 模型求解流程图Fig.2 Flowchart of model solution

3 算例分析

为验证本文所提方法的有效性，以文献［21］构造的电-气综合能源系统为基础，增加1 台装机容量为150 MW 的风电机组与3 台功率为20 MW 的P2G设备构成的P2G场站，构建了含P2G的电-气综合能源系统。其中，将压缩机入口与管道连接处视为一个节点，气井及气井处压缩机视为气源，VPD 形状参数由文献［22］中风电出力数据拟合，P2G 设备参数根据文献［19］进行设置，风电机组参数、VPD 分布拟合参数和P2G 设备参数分别如附录A 表A2—A4 所示。仿真环境为MATLAB R2020a，求解器为Gurobi 9.0.3。为研究风电出力不确定条件下P2G 设备对电-气综合能源系统协调调度的影响，设置了4种不同场景，具体如下：场景1，考虑P2G 设备响应特性，P2G 设备名称为a1—a3；场景2，采用文献［11］中无响应特性P2G模型，设备名称为b1—b3；场景3，考虑P2G响应特性，参考文献［23］中模型，将场站内所有的P2G 设备看成一个整体，相应的设备名称为c1；场景4，P2G设备不工作，即不考虑P2G设备。

对上述4 种场景进行仿真，不同场景下的调度结果如表1 所示。不同场景下的风电机组出力如图3所示。P2G设备运行状态图如图4所示。

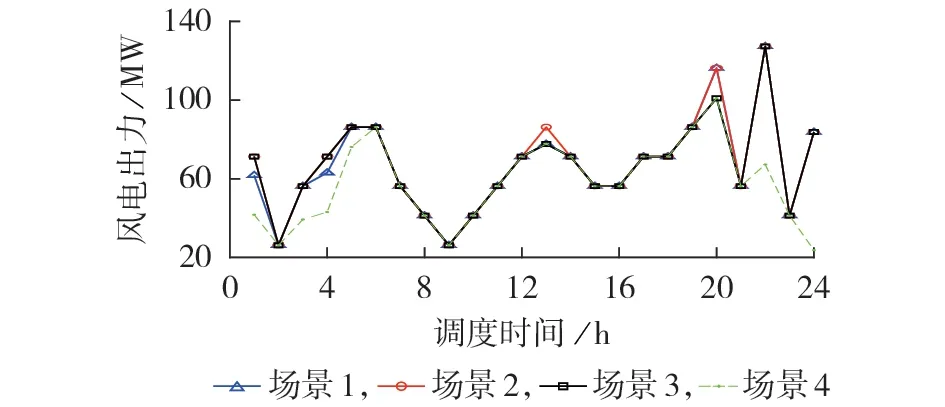
图3 不同场景下的风电出力Fig.3 Wind power output under different scenarios

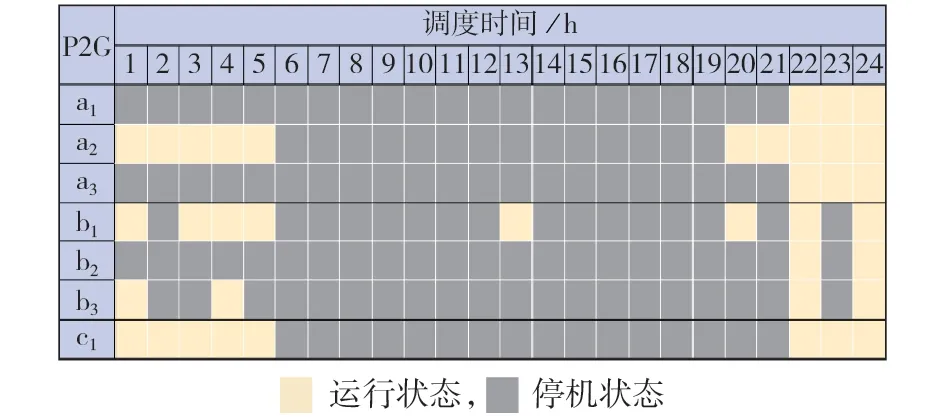
图4 P2G设备运行状态图Fig.4 Operation state of P2G facilities

由表1 及图3 可知，与场景4 中无P2G 设备的情景相比，场景1—3中P2G设备的使用可以提升风电消纳水平，有效减少弃风量，降低系统运行成本。这是由于一方面P2G 设备的投入减少了弃风，降低了风电惩罚成本，另一方面P2G 设备可以生成甲烷注入到天然气管道，降低能源消耗成本。但不同P2G模型产生的调度结果存在明显差异。

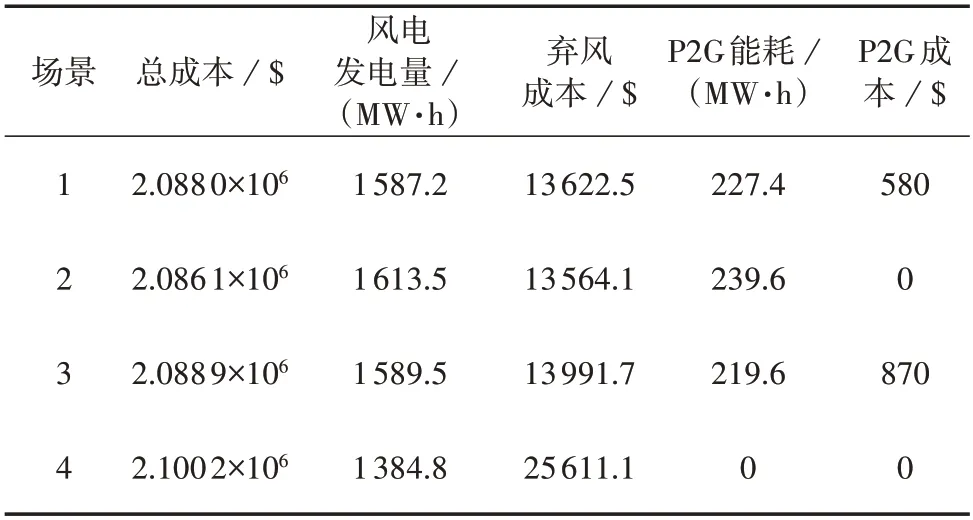
表1 不同场景下的调度结果对比Table 1 Comparison of scheduling results under different scenarios

由表1 及图3、4 可知，场景2 忽略了P2G 设备响应特性，调度方案给出的P2G 设备运行状态违反物理上的最小停启时间约束。因此，该调度方案虽然成本更低，但夸大了风电消纳能力以及系统运行经济性，实际上不可行。场景1 考虑了P2G 设备的响应特性及相应的停启时间约束。首先，在部分零弃风时刻，例如调度时间为2、21、23 h 时，系统无需运行P2G 设备就可以完全消纳风电，但是由于最小运行时间约束，此时P2G设备仍要继续运行，风电出力却无法进一步提升，并且由于电能到甲烷的转换过程中会产生能量损失，系统总运行成本增加。其次，在部分弃风量较小的时刻，由于响应特性以及停启成本，启动P2G设备也不再具有经济性。例如，调度时间为13 h 时仅有少量弃风，P2G 设备运行将导致总成本增加，此时P2G设备处于停机状态；调度时间为1、4 h 时，启动1 台P2G 设备基本可以消纳大部分风电，而启动2 台设备反而会增加总成本，故仅有1台设备启动。此外，由图3 和图4 可知，场景3 忽略了不同P2G 设备间的组合，简单地将P2G 场站看成整体进行调度，虽然调度结果满足设备运行的物理约束，但无法发挥P2G 消纳风电的灵活性。例如调度时间为20 h 时，弃风量较低，且相邻时刻无弃风，由于场景3 简单地将P2G 设备视为整体，其最小运行功率远大于场景1 中单台设备，在弃风量较小的情况下，由于转换过程中能量损失，此时启动P2G设备不再具有经济性，产生弃风。

不同场景下的P2G 设备出力如图5 所示。场景1、2下的火电机组出力如图6所示。

由图5 与图6 可知，场景2 下的火电机组调度出力小于场景1，这是由于场景2认为P2G 设备可在弃风时刻立刻启动，没有考虑设备停启时间约束及连续运行过程中产生的电能需求。例如当调度时间为2、21、23 h 时，风电可完全消纳，P2G 运行无法进一步提升风电出力，但由于P2G设备的响应特性，它们仍应处于停机状态，所以火电机组需增加出力提供P2G 所需电能。显然，由于场景2 忽略响应特性，火电机组调度结果小于实际运行要求，这会导致系统功率不平衡，甚至引发频率稳定问题。

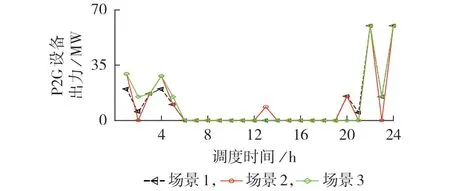
图5 不同场景下的P2G设备出力Fig.5 Output of P2G facilities under different scenarios

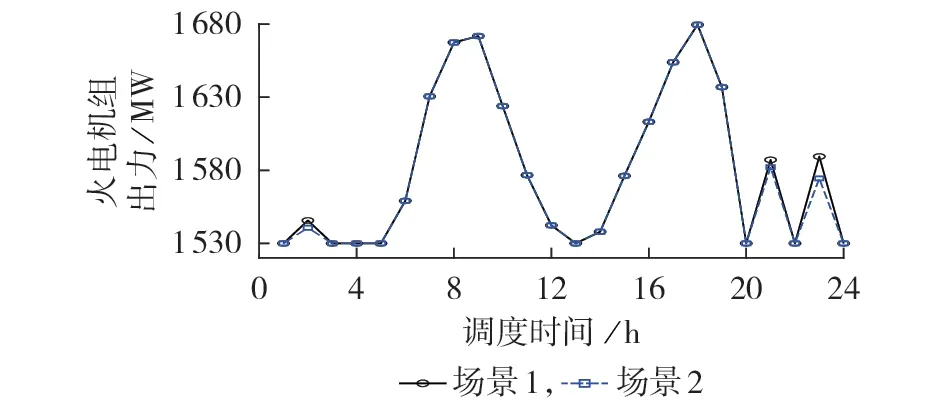
图6 场景1、2下的火电机组出力Fig.6 Output of thermal power units under Scenario 1 and Scenario 2

由上述对比分析可知，P2G 设备可以有效提升风电消纳水平，降低系统运行成本，但模型不精确无法反映P2G 设备实际运行特性，会导致调度结果不可行或低估P2G 设备灵活性，引发一系列问题。忽略响应特性会导致P2G设备频繁停启违反实际的运行约束，而由这种违反实际运行约束的调度方案得来的更低运行成本实际上也很难达到。简单地将P2G 场站看成整体进行调度，忽略其内部不同P2G设备之间的组合，使得调度范围小于P2G 设备实际运行范围，无法充分发挥P2G设备的灵活性，降低了系统运行的经济性。

4 结论

本文在电力、天然气系统紧密耦合的背景之下，针对现有含P2G 设备的电-气综合能源系统模型的不足，基于P2G 设备响应特性，构建了含P2G 的电-气综合能源系统优化调度模型，研究了风电出力不确定条件下综合能源系统的优化调度问题。

不同场景下的仿真结果表明考虑P2G响应特性对电-气综合能源系统的可靠、经济运行有重要意义。忽略P2G设备响应特性会夸大系统风电消纳能力，调度结果与实际设备运行状态有较大偏差，无法满足P2G 设备实际运行条件，增加了系统实际运行成本，且会导致火电机组出力低于实际需求，引发功率不平衡及频率问题。将P2G场站简单视为整体进行调度，则无法发挥P2G设备灵活性，低估了P2G设备风电消纳能力与运行经济性。本文仅考虑电力与天然气系统之间的耦合关系，随着热电联产机组装机容量不断增加，电、气、热之间耦合关系不断加深，在本文研究基础之上，未来还有必要进一步构建考虑P2G的电-气-热综合能源系统调度模型。

附录见本刊网络版（http：//www.epae.cn）。