基于Fluent的管道内水合物浆液流动特性数值模拟

钟一华，卿亚丽，杨海川，李璐伶，刘 婷，蒋 鹏

（1.天津大学 管理与经济学部，天津300072；2.深圳市燃气集团股份有限公司，广东 深圳518049；3.广东大鹏LNG公司，广东 深圳518040）

天然气水合物是由甲烷、乙烷和二氧化碳等气体分子与水形成的复杂笼型晶体[1,2]。在油气输送系统中，特别是在高压低温条件下，水合物颗粒极易生成，在流动过程中会不断聚集，最终部分堵塞或完全堵塞管道，造成严重的设备与安全问题[3]。故有必要研究水合物浆液在管道中的流动特性和颗粒行为。

对管道中水合物浆液流动特性的研究主要基于实验和理论计算。Carmargo等[4]在高压（9 MPa）和低温（258~338 K）环路中，对水合物在含沥青质的原油中的形成过程和流变特性进行了实验。之后，Sinquin等[5]利用同样的高压环路，对天然气水合物在油基体系中的流变特性进行了测试，并建立了考虑颗粒聚集和微絮凝破坏机理的水合物浆液流变行为数学模型，该模型已运用在CSMHyK软件中。Gainville等[6]使用IFP-Lyre高压环路研究了水合物浆液在层流和湍流中的压降。Joshi等[7]基于埃克森美孚的高压环路实验装置，研究了水基天然气水合物形成机制。虽然高压环路实验提供了天然气水合物在管道中形成、成核和团聚等信息，但复杂的实验设备和严格的高压条件限制了对水合物浆液在管道流动堵塞方面的研究。利用制冷介质（如HCFC、THF、TBAB和R11）替代碳氢水合物的浆液流动低压实验，逐渐成为研究水合物浆液流动特性和颗粒行为的有效方法[8]。但在实验测量方面也有一定的局限性，如在测量颗粒的体积分数分布和速度矢量分布等方面存在技术困难。

随着固液两相理论的发展，利用计算流体力学（CFD）来研究水合物浆液在管道中的流动特性逐渐成为研究热点。Jassim等[9]运用Fluent对天然气输送中的水合物沉积过程进行了模拟，但该研究仅考虑了天然气对水合物的单向影响。Balakin等[10,11]利用STAR-CD对R11（一氟三氯甲烷）水合物浆液在管道中的流动情况进行了计算。Sule等[12]运用ANSYS CFX对水合物的形成过程进行了考察，并研究了流动速率、管道直径和水相比例对管道温度分布的影响。此外，王武昌等[13,14]对HCFC-141b和THF水合物浆液的流动行为进行了研究，并提出凝聚概率来判断管道的流动安全性。韦雪蕾等[15]基于欧拉双流体模型，模拟了不同粒径的水合物浆液在水平管道中的流动情况。

目前，考虑了水合物颗粒流动过程中的粒径变化和粘度特性的浆液流动数值模型较少，以及考虑了水合物颗粒密度和颗粒粒径变化对管道压降和颗粒体积分数分布影响的研究较少。本文以欧拉双流体模型和RSM湍流模型为基准，通过编制UDF对水合物颗粒粒径和水合物浆液粘度进行自定义，基于ANSYS Fluent 14.0建立了R11水合物浆液在管道中的流动模型，并对水合物颗粒在较低流速下的沉积特性进行了分析。

1 数学模型与模拟

1.1 基本控制方程

采用欧拉双流体模型来描述水合物浆液在管道内的固液流动。假设流动过程只含有水合物颗粒及水两相，水合物为光滑球形颗粒，忽略相间质量和热量传递，则液相和颗粒相的连续性方程可分别表示为：

式中，α为体积分数，%；ρ为密度，kg/m3； 为拉普拉斯算子； 为速度矢量，m/s；下标s和l分别表示水合物颗粒相和液相。

液相和水合物相的动量守恒方程可用Navier-Stokes方程表示为：

式中，p为压力，Pa；g为重力加速度，m/s2； 和 分别为颗粒相和液相的应力张量，Pa；ps为颗粒压力，Pa；M为相间动量交换系数，kg/(m·s)2；μl、μs和ζs分别为液体、固体和流体的剪切粘度，kg/(m·s)；I为单位向量。

颗粒压力可表示为：

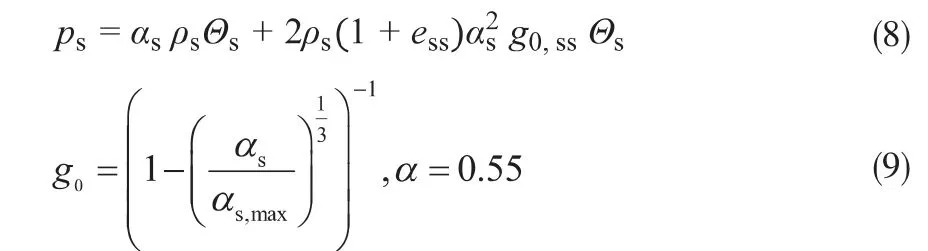
式中，Θs为颗粒温度，K；ess为颗粒恢复系数，ess=0.9；g0,ss为颗粒径向分布函数，其表达如式(9)所示；αmax为颗粒最大装填系数。

假定混合相粘度（μm）与固相颗粒粘度（μs）和液相粘度（μl）成线性关系，其表达式为式(10)。对于R11水合物浆液，混合相粘度与固相分数有关，可用Brinkman方程[10]来拟合，其表达式为式(11)。结合式(10)和式(11)，则固体颗粒粘度（μs）可表示为式(12)。

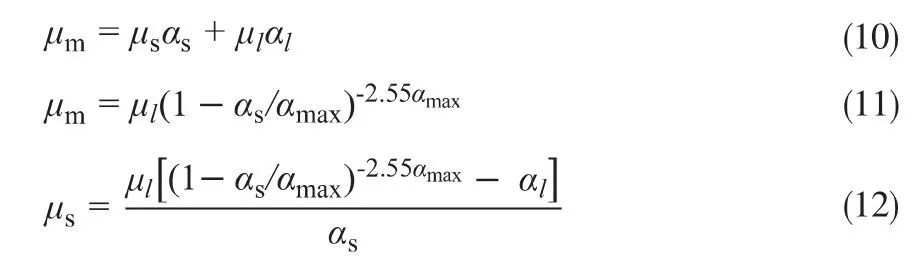
相间动量传递量M主要考虑相间曳力作用，Mls可表示为：

式中，Kls为Gidaspow曳力模型的交换系数[16]；CD为曳力系数；Res为相对雷诺数；ds为固体颗粒粒径，μm。

在流动中，水合物颗粒会经历形成、成长、聚并和聚集阶段，导致粒径不断变化。水合物颗粒粒径（ds）可用Camargo模型来进行计算[17]，其表达式为：

式中，d1为颗粒初始直径，μm；γ为剪切速率，s-1；Fa为颗粒间粘附力，nN；fr为分形维数，由实验值决定；Balakin等[11]利用群体平衡模型，结合实验数据，经回归得到d1=7 μm，fr=1.83，Fa=1.75 nN。

1.2 数值模拟

采用的弯曲管道三维模型如图1所示，该模型依据Balakin等[11]的R11水合物浆液管内流动实验数据建模。其在实验中测定了R11水合物在常压环流管路中的阻力特性及流动形态，但对于水合物颗粒在管道中的分布仍未明晰。

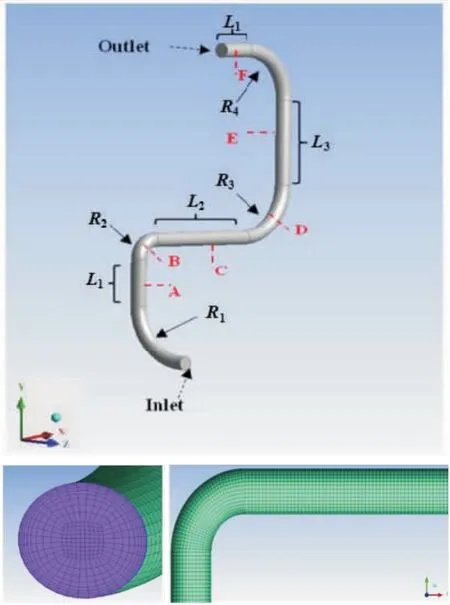
图1 管道三维模型

图1 所示管道的内径为45.2 mm，大写字母A-F表示管道截面编号。此外，利用ICEM对管道进行六面图网格划分，水平、弯曲及进出口端面的网格划分情况也如图1所示，对近壁处的网格进行加密处理，以提高计算精度。R11水合物浆液的基本性质如表1所示。

表1 R11水合物浆液的两相基本性质

采用雷诺平均Navier-Stokes方程（RANS）来计算流体的湍流特性。本文应用雷诺应力模型（RSM）来求解水合物浆液在管道流动中的湍流现象。与标准k-ε模型相比，RSM不采用Boussinesq假设，而是直接计算雷诺应力项，故求解时间更长。RSM模型表达式为：

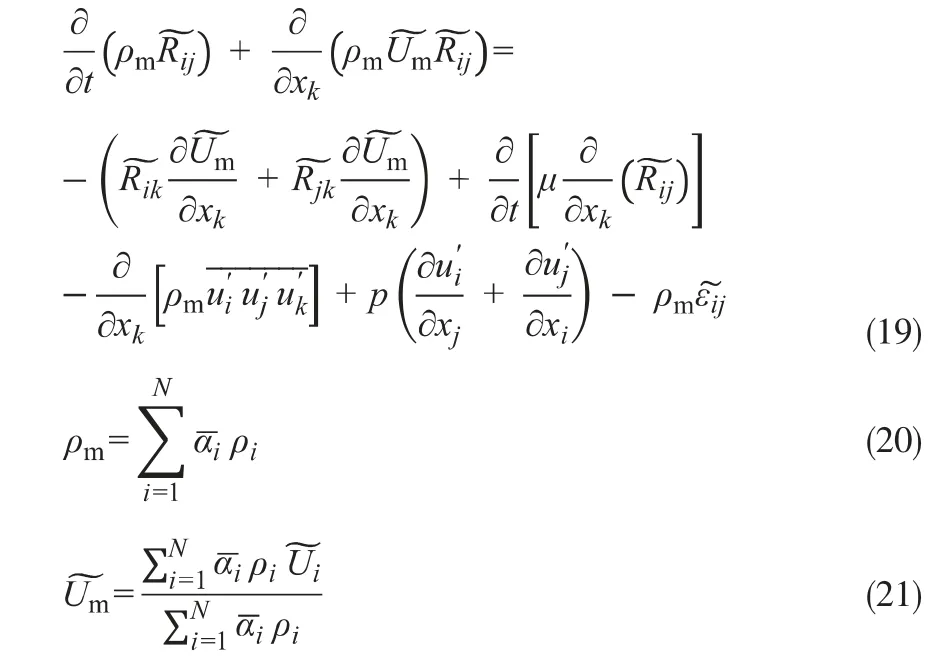
利用Fluent 14.0对上述模型进行求解。入口边界条件为水合物浆液的速率、湍流强度、水力直径和颗粒相分数，此外设定参考运行压力为101325 Pa，参考点为（0.35 m,0.814 m,0）。出口边界条件设置为压力出口，其表压为0。在壁面，颗粒相和液相两相无滑移现象。压力-速度耦合使用PC-SIMPLE算法，并以一阶迎风算法对动量方程、体积分数、湍流动量和耗散方程进行离散求解，残差设置为10-5。

1.3 网格独立性验证

对于水合物浆液在弯曲管道中的湍流流动模拟，为减少数值模拟网格误差，以水为流体介质，计算了网格总数从156128到1466172个范围内，流体压降梯度的变化情况。模拟采用的流速为1.50 m/s，结果如图2所示。由图2可知，随着网格数的增加，压降梯度先急剧下降，当网格数大于220000后，压力梯度开始趋于平稳，再增加网格数量，结果基本不变。因此，本文选取224721个网格作为后续计算网格数。

图2 网格独立性验证

1.4 模型验证

为验证本文所建数值模型的可靠性，利用Fluent 14.0，在水合物体积分数分别为0、5%、14%和38%的条件下，对流速为0.80~3.90 m/s的管道阻力特性进行了模拟，并将水合物浆液流动压降梯度的预测值与Balakin等[18]测得的实验压降梯度进行了对比，如图3所示。由图3可知，在相同的体积分数下，压降梯度的模拟值与实验值在不同流速下均吻合较好，最大误差在10%范围内，显示出所建模型的正确性，故可用该模型来研究水合物浆液在管道流动的压降及浓度场分布特性。另一方面，随着流速增加，压力梯度也呈上升趋势，该现象可由Darcy-Weisbach[19]方程来描述，即管道内压降梯度与流体速率存在正相关关系。当水合物体积分数在0~14%时，在相同流速下的压降基本相同，但当水合物体积分数达到38%，压降明显增大，此时水合物粘度系数增大，表现出非牛顿流体特性。

图3 不同流速和水合物颗粒体积分数下压降梯度实验值和模拟值对比

2 结果及讨论

2.1 水合物颗粒密度的影响

在水合物颗粒体积分数为38%、流速为1.50 m/s的条件下，采用欧拉双流体模型和RSM湍流模型，考察了水合物颗粒密度分别为800 kg/m3、1138 kg/m3和1300 kg/m3时对水合物浆液压降梯度和颗粒平均粒径的影响，如图4所示。

随着水合物颗粒密度从800kg/m3增加到1300kg/m3，压降梯度从548 Pa/m上升到1160 Pa/m，这主要是由于流固交换系数导致阻力增大和水合物颗粒沉积所致。同时可知，增大颗粒密度，水合物平均直径从约98.5 μm略微上升至101 μm，其原因为颗粒沉积引起固体颗粒团聚，使得颗粒粒径增加。

水合物颗粒的体积分数分布反映了颗粒的聚集特性。图5显示了在水合物颗粒密度分别为800 kg/m3和1300 kg/m3情况下，管道不同位置截面处（截面位置见图1中A~F）水合物颗粒体积分数分布图。此外，水合物颗粒垂直于流动方向的速度矢量图也显示在了图中。模拟初始条件为水合物颗粒体积分数和流速分别为38%和1.50 m/s。当颗粒密度为800 kg/m3时，截面A~F靠近中心处的水合物浓度高于壁面处的浓度，这主要是由于二次流的影响，将水合物颗粒向中心集聚。当水合物密度为1300 kg/m3，由于离心作用，水合物颗粒向近壁面累积，使截面A的底部和截面B的左侧水合物颗粒体积分数较高，其最大值为38.6%。另一方面，对于截面C到截面F，颗粒分散相对均匀，水合物颗粒体积分数分布差异较小。

图5 水合物颗粒密度对其体积分数分布的影响

2.2 水合物颗粒粒径的影响

水合物颗粒的粒径也会影响其流动阻力特性和体积分数分布。根据Camargo颗粒粒径计算模型（式(18)），水合物颗粒在管道中流动受剪切速率等影响，会发生聚并，引起粒径变化。由图4(b)所示，在水合物颗粒基准密度下，其平均粒径为100 μm。此外，还考察了颗粒平均粒径在70~120 μm变化时，水合物颗粒的压降梯度及体积分数分布的变化，结果如图6所示。模拟初始条件为：水合物浆液的入口流速为1.50 m/s，水合物颗粒体积分数为38%。当粒径为70 μm时，压降梯度值约为1010 Pa/m，当粒径为120 μm时，压降梯度降低至860 Pa/m。随着水合物颗粒平均直径的增加，水合物颗粒压降梯度减小。这主要是因为大粒径的水合物向管壁沉积，使得管道内有效流速增加，雷诺数增加，故压降出现降低趋势。

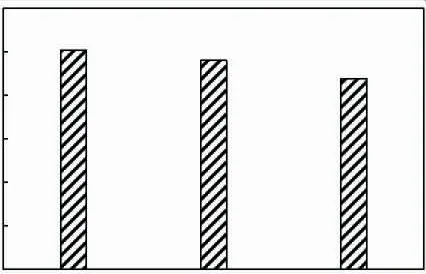
图6 水合物颗粒平均粒径对压降梯度的影响

图7 显示了水合物颗粒平均粒径对不同截面处的水合物颗粒体积分数分布的影响。随着颗粒平均直径的增大，同一截面上的颗粒体积分数分布存在显著差异。在平均粒径为70 μm时，颗粒在不同截面处的分布较为均匀，但当平均粒径增大到120 μm时，在所示的六个截面处，近壁面的水合物颗粒体积分数高于管道中心处，这主要是大颗粒水合物的聚集，并在离心力的作用下，又在管壁处聚集，引起了管道流通面积的减少，甚至可能导致管道堵塞。

图7 水合物颗粒平均粒径对其体积分数分布的影响

2.3 水合物的沉积特性

油气管道中水合物颗粒的聚集与沉积是对安全运行的巨大挑战。水合物沉积会增大压降梯度，抑制流体流动，导致管道堵塞。在较高的流速下，流体流动呈现均匀状态，但当平均流动速度小于临界值时，水合物颗粒便开始沉积在管道中。为量化沉积厚度，以水合物体积分数为14%计算，设定水合物浆液流速为0.10～0.40 m/s，水合物颗粒的密度和粒径如表1所示，对水合物在管道中的体积分数分布进行了计算。

图8 显示了在不同流速（0.10 m/s、0.25 m/s、0.40 m/s）下截面F的水合物体积分数分布云图。在截面的上部区域，水合物体积分数非常低，接近于0。然而，在截面的中间区域，水合物浓度开始变得均匀分散。水合物体积分数呈向截面底部逐渐增加的趋势。当流速分别为0.10 m/s和0.25 m/s时，最大水合物体积分数为0.55，水合物颗粒已在管道底部形成了固定床层，当流速增大到0.40 m/s时，固定床层消失。如图9所示，流速从0.10 m/s增加到0.40 m/s时，沉积厚度由14 mm降低至0 mm。这主要是由于以下原因导致的：R11水合物颗粒的密度大于水，水合物颗粒沉积到以重力为主的底部区域；在横截面的中部区域，颗粒浮力和阻力的组合与重力竞争，使颗粒分布均匀；由于流速的增加，湍流强度及剪切力增强，水合物颗粒的分散能力增强，沉积厚度降低甚至消失。

图8 不同流速下的水合物颗粒体积分数分布（F截面）

图9 水合物颗粒沉积厚度与流速的关系

3 结论

基于欧拉双流体模型和RSM湍流模型，并引入了Brinkman水合物粘度模型和Camargo粒径模型，利用Fluent 14.0对管道内水合物浆液流动和沉积特性进行了三维数值模拟。网格独立性分析发现，当网格数大于220000后，压降梯度开始趋于平稳。对比实验测定的管路压降梯度，发现在不同水合物体积分数和流速下的压降梯度的模拟值与实验值误差均小于10%，验证了所建模型的准确性。

水合物浆液的压降梯度和颗粒平均尺寸均随着水合物密度的增加而增大，但水合物颗粒粒径的增加使得压降梯度降低。此外，增大水合物颗粒密度和平均粒径均促进了水合物向管壁聚集，出现了较大的体积分数分布梯度。水合物颗粒沉积特性表明，对于体积分数为14%的水合物浆液，当流体速率小于0.40 m/s时，水合物颗粒会沉积在管壁上，引起管道堵塞。当流速为0.10 m/s时，床层厚度可达14 mm，随着流速的增加，水合物颗粒沉积床层高度减小。