连续变量量子密钥分发系统调制方差全局优化方法研究*

马 荔, 李 扬, 杨 杰, 黄 伟, 罗钰杰, 徐兵杰

西南通信研究所 保密通信重点实验室, 成都610041

1 引言

量子密钥分发(quantum key distribution, QKD)[1–3]基于量子力学原理, 可实现信息论可证安全的密钥分发, 是量子信息技术中最接近实用化的研究方向之一. 其主要技术途径可分为离散变量(discrete variable, DV)[4,5]和连续变量(continuous variable, CV)[6–12]两大类. 连续变量量子密钥分发(continuous variable quantum key distribution, CV-QKD) 技术采用光场的正则分量来编码密钥信息, 因其与传统光通信网络兼容性好且具备高码率潜能, 极具发展前景. 最常见的CV-QKD 协议是GG02 类协议[13,14], 其量子态制备简单、易于实现, 是目前广泛使用的CV-QKD 协议.

典型的CV-QKD 系统包括量子信号传递与数据后处理两个步骤. 提高CV-QKD 系统的性能, 通常从两方面开展研究. 一方面是优化CV-QKD 系统的光电关键技术, 比如, 过噪声控制[15,16]、后处理纠错能力优化[17–22]; 另一方面是优化CV-QKD 系统的协议参数[23]. 本文主要从CV-QKD 系统协议参数优化的角度开展研究.

在实际的CV-QKD 系统中, 当信道传输距离发生变化时, 需要相应地改变量子信号的调制方差以优化系统性能. 在实际系统中, 信道透射率、过噪声、电噪声、探测效率在外界环境变化不大的情况下通常变化不大, 调制方差将显著影响系统的信噪比, 而后处理中数据协商的实际效果与数据信噪比紧密相关,因此, 调制方差直接影响系统安全码率的大小. 针对CV-QKD 系统的调制方差最优化问题是CV-QKD系统性能优化的重要问题. 已有的调制方差优化方法通常假定在某个特定传输距离下, 数据协商的协调效率和纠错译码的误帧率为常数[16,24], 然后计算与最大安全码率相对应的最优调制方差. 然而, 在实际CV-QKD 系统中, 对于确定的数据协商和纠错译码算法, 很难针对不同的调制方差都设计相应的纠错矩阵来维持数据协商的协调效率β为常数, 纠错的误帧率FER 也会随调制方差VA的变化而变化. 由于协调效率和误帧率显著影响系统安全码率的大小, 因此在进行实际系统最优调制方差计算时, 应当综合考虑调制方差对误帧率、纠错效率等参数的影响.

为解决这一问题, 本文提出一种CV-QKD 系统调制方差全局优化方案, 针对确定的数据协商和纠错译码算法, 给出协调效率和误帧率与调制方差之间的函数关系. 基于定量分析协调效率和误帧率随调制方差的变化关系和制约特性, 给出系统安全码率与调制方差之间的函数关系, 最终给出使系统安全码率最大化的最优调制方差参数选取方法, 从而提升实际CV-QKD 系统性能.

2 系统安全码率与调制方差的函数关系

反向协调下[25], 对于无限码长情形, CV-QKD 系统在任意联合攻击下的安全码率公式为:

其中, FER 为纠错译码的误帧率,β为数据协调效率,IAB是发送端Alice 和接收端Bob 之间的经典互信息,χBE是Bob 和窃听者Eve 之间的量子互信息.

在已有研究中, 通常认为影响CV-QKD 系统安全码率的主要因素是协调效率, 为实现长距离和高码率, 要求系统具备高协调效率. 以多维数据协商和MET-LDPC 矩阵译码为例, 制约协调效率的主要因素为协商算法选择、度分布函数性能以及校验矩阵的生成. 协调效率描述的是后处理能够提取出来的密钥比特数与Alice 和Bob 之间的二进制互信息之间的比值, 0≤β≤1,β越接近1, 即越接近香农极限, 则系统安全码率越高、可达到的最远传输距离越长. FER 会影响安全码率的大小, 但不会影响安全码率的有无.因此为了提高系统的实用性, 增强系统的可靠性, 应该同时提升协调效率并尽量降低误帧率, 以获得更高的安全码率.

安全码率的具体计算可参考文献[14,26,27], 以GG02 协议为例, 其中IAB可表示为:

基于上述安全码率计算过程可知,IAB和χBE可表示为系统信道透射率T、过噪声ε、电噪声vel、探测效率η和调制方差VA的函数. 当传输距离一定时, 对于确定的CV-QKD 系统, 一般可认为其信道透射率T、过噪声ε、电噪声vel、探测效率η近似为常数, 可将IAB和χBE表示为调制方差VA的函数, 即IAB=fIAB(VA) 和χBE=fχAB(VA), 则安全码率公式(1)可以表示为以调制方差VA为唯一变量的函数, 进而可以基于优化VA对安全码率进行最大化.

对于一个确定的译码矩阵, FER 随调制方差VA的变化关系是实际实验可观测的, 可根据纠错矩阵的随VA变化的实际纠错成功率进行数值拟合, 进而得到关系式FER=fFER(VA).

综上, 安全码率可表征为VA的函数:

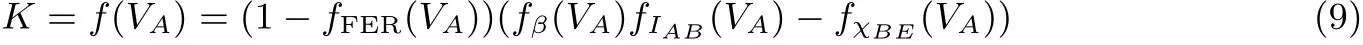
由此可知, 安全码率可以视为以调制方差VA为唯一变量的函数. 则相应地, 安全码率的优化问题实际上可以视为以调制方差VA为参数的优化问题.

3 调制方差全局优化方法

根据上述理论推导, 我们提出了一种基于调制方差的安全码率优化方案, 优化流程如图1 所示.

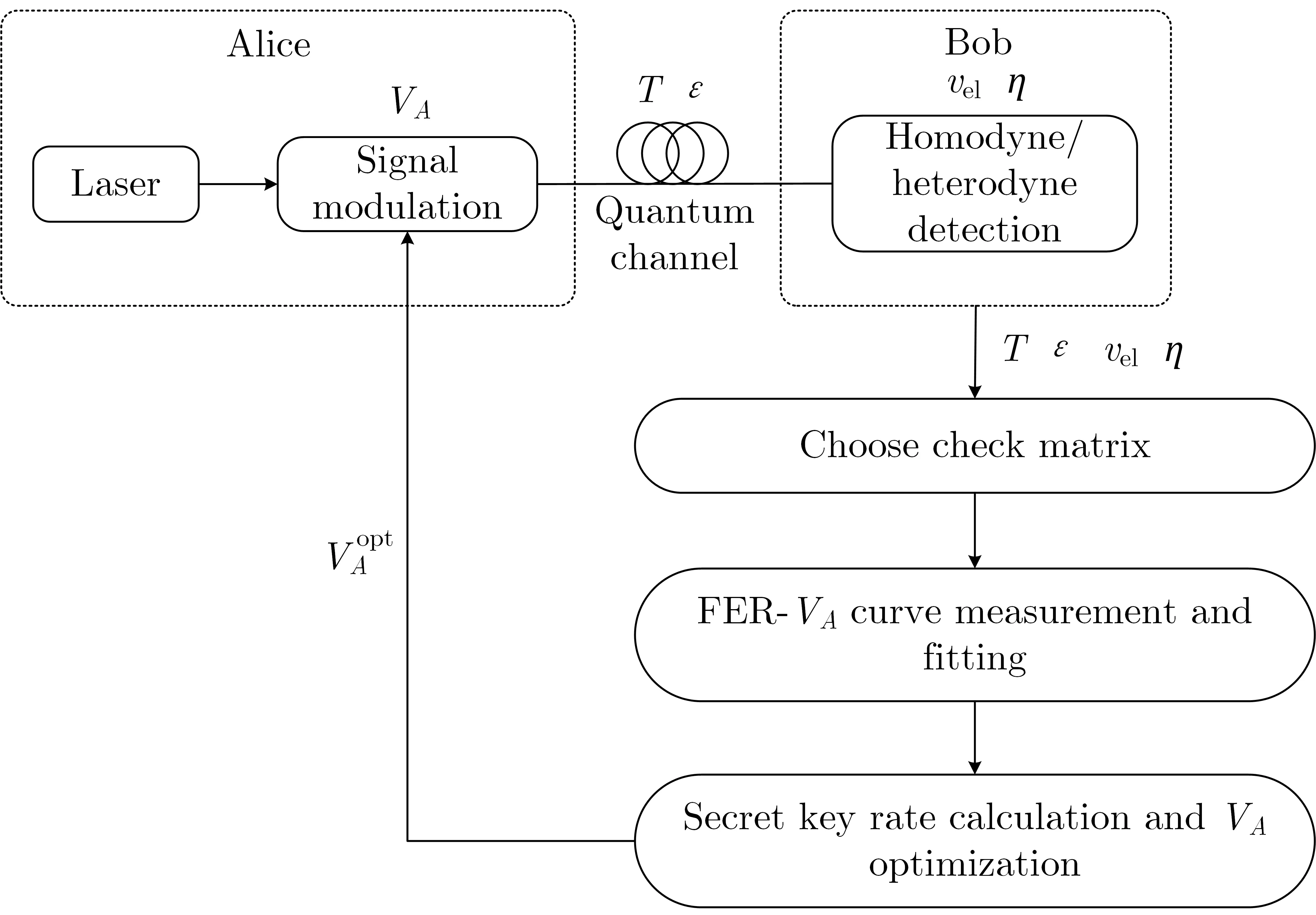
图1 调制方差全局优化流程Figure 1 Global optimization process of modulation variance

第一步, 首先获取系统参数. 对于确定的CV-QKD 系统, 在特定的传输距离下, 信道透射率T、过噪声ε、电噪声vel、探测效率η受调制方差VA的影响很小, 可以不失一般性地近似为常数. 上述参数均可通过实际观测得到[28].

第二步, 分别获取β-VA和FER-VA的函数关系. 根据第一步中获取的系统参数, 选择合适的VA范围(如: 0～20[24]/0～30[29]), 并计算相应的SNR 范围. 根据SNR 范围, 选择适用于对应SNR 范围合适的纠错矩阵H. 纠错矩阵确定后即可确定矩阵码率R, 则β-VA的函数关系可基于矩阵码率R和信噪比SNR 计算得到, 由于协调效率范围应满足0≤β≤1, 进一步可缩小对应调制方差VA可选范围, 计算公式见公式(8); 而FER-VA的函数关系则需要依据实际选用的纠错矩阵的纠错译码能力进行曲线数值拟合得到, 详细的拟合步骤在下一小节进行具体介绍.

4 结果与讨论

上一节介绍了基于调制方差的安全码率优化方案的处理步骤, 本节以信道传输距离为50 km 的典型条件为例介绍具体的计算分析方法.

第一步, 我们参考文献[24,26] 设定CV-QKD 系统状态参数: 电噪声vel=0.041, 过噪声ε=0.005,探测效率η=0.606, 信道衰减系数为α=0.2 dB/km, 根据传输距离L=50 km 计算T=10−αL/10. 第二步, 对于信道传输距离为50 km 的条件下, 我们选择文献[30] 中码率为0.1 的度分布函数生成校验矩阵用于纠错译码, 对0 ＜VA＜20, 步长0.01 的数据逐一生成256 个块的数据量(每个块长为106), 测量得到对应FER, 即可得到的FER-VA曲线的测量和拟合结果如图2 所示. 从图2 可以看出, 当0 ＜VA＜2.6 时, FER = 1, 表明纠错全部失败; 当VA大于3 时, FER = 0, 表明纠错全部成功; 而在2.6≤VA≤3时, FER 随VA 的增加而降低, 如图2 中实线所示; 相应地, 纠错成功率1-FER 随VA的增加而提高, 如图2 中虚线所示. 因此, FER-VA的曲线关系主要拟合2.6≤VA≤3 的变化部分, 其余部分为常数.

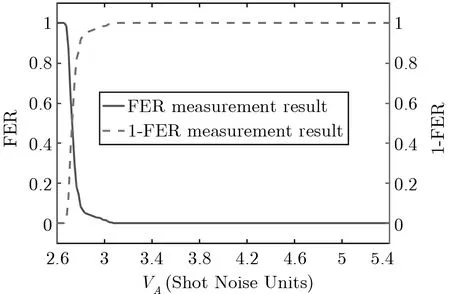
图2 FER-VA 曲线的测量结果和(1-FER)- VA 曲线对比(50 km 传输距离, 码率0.1)Figure 2 Comparison between measured results of FER-VA curve and (1-FER)- VA curve (L = 50 km, R = 0.1)

常见的拟合函数有正弦拟合、高斯拟合和傅里叶拟合, 综合考虑到拟合效果和计算复杂度, 我们统一采用7 阶拟合函数, 对应的拟合结果如图3 所示, 其中测量结果为实验观测结果, 图中可看出拟合结果都取得了很好的一致性.

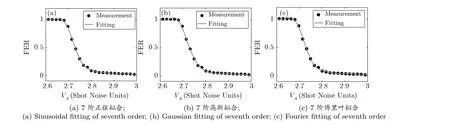
图3 FER-V A 拟合结果Figure 3 Fitting result of FER-V A

进一步, 我们对比了三者的拟合误差: 和方差(sum of squares due to error, SSE)、确定系数(coefficient of determination)R-square, 和均方根(root mean squared error, RMSE), 对比结果如表1 所示,从表1 结果可知7 阶傅里叶拟合误差更小, 因此我们采用该拟合函数对FER-VA曲线进行拟合.

表1 正弦拟合、高斯拟合和傅里叶拟合误差对比Table 1 Error comparison of sinusoidal fitting, Gaussian fitting, and Fourier fitting

最终得到的分段7 阶傅里叶拟合函数如公式(10) 所示:

依据公式(8), 将相关系统参数带入即可以得到协调效率和调制方差之间的数学关系式:

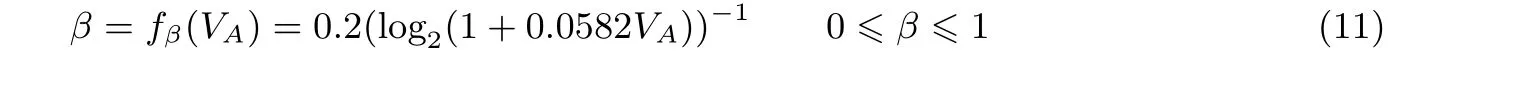
其相应的变化曲线如图4 所示. 从图4 可以看出, 调制方差VA和协调效率β之间为负相关, 即当VA在一定范围内变化时, 协调效率随调制方差增大而降低, 如图4 所示.

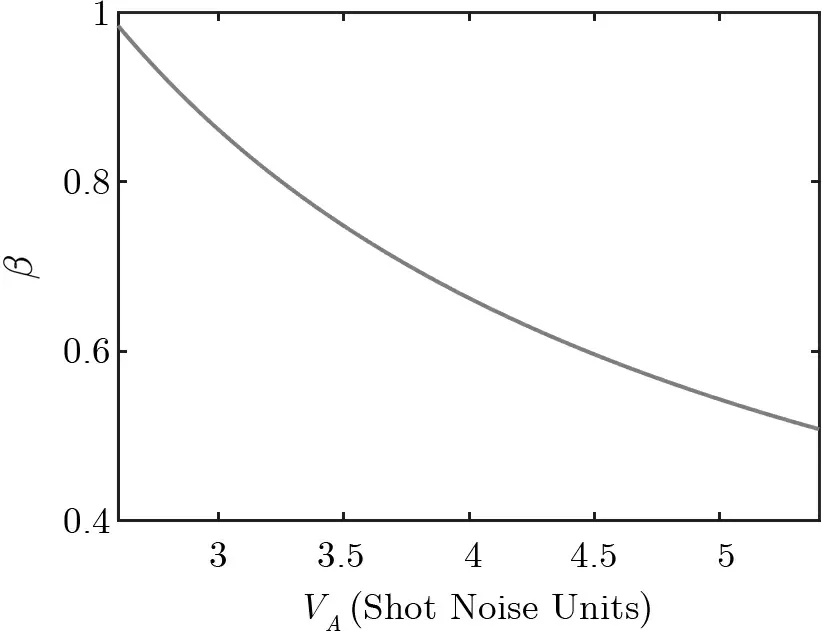
图4 β-V A 曲线(50 km 传输距离, 码率0.1)Figure 4 Curve of β-V A (L=50 km, R =0.1)

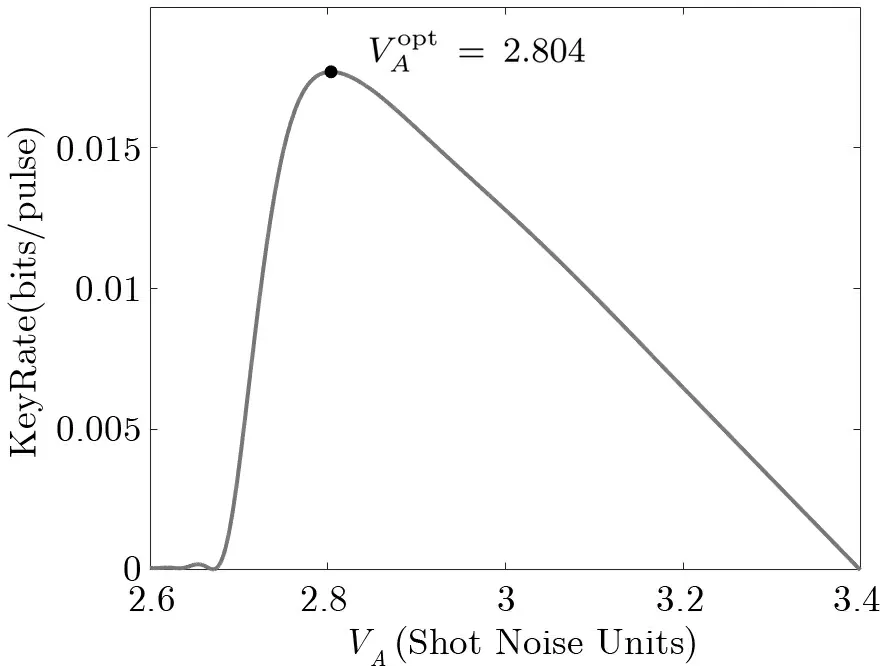
图5 VA-KeyRate 曲线, 最优调制方差=2.804 (50 km 传输距离, 码率0.1)Figure 5 Curve of VA-KeyRate, optimal modulation variance=2.804 (L=50 km, R =0.1)

我们对以下三种调制方差的选择方法进行对比, 对应选择CV-QKD 系统参数为vel= 0.041,ε=0.005,η= 0.606,α= 0.2 dB/km,T= 0.1, 且选用R= 0.1 码率的纠错矩阵进行纠错: 1) 根据经验调节适用于R= 0.1 码率的信噪比范围, 使得SNR = 0.161/SNR = 0.158, 可对应实现协调效率β=92.85%/β=94.50%, 对应参数可得到调制方差的对应结果; 2) 在协调效率和误帧率为常数的情况下,如:β= 92.00%, FER = 0 时, 得到最优调制方差; 3) 本文提出的优化方案. 采用相同的数据协调和纠错译码方法, 对比结果如表2 所示, 对于方法一, 不考虑系统参数和数据后处理能力, 根据经验选择SNR 和协调效率β, 无法保证安全码率最大化; 对于方法二, 不考虑调制方差对误帧率、协调效率的影响, 而不结合实际后处理能力, 导致实际协调效率无法达到目标值, 也无法保证安全码率最大化; 而采用本文方法, 考虑调制方差对协调效率和误帧率的影响, 根据最优调制方差可得,K= 0.0177 bits/pulse, 对比方法一和方法二, 本方法安全码率显著提升. 综上表明, 仅通过经验或固定协调效率和误帧率的方法来确定调制方差, 无法达到最优系统性能, 本方法通过明确的优化方案实现安全码率最大化.

进一步地, 针对相同的CV-QKD 系统状态参数, 即vel= 0.041,ε= 0.005,η= 0.606,α=0.2 dB/km, 我们以文献[30] 的度分布函数为例, 生成了码率为0.1、0.05、0.02 的纠错矩阵, 分别适用于当传输距离L约为50 km、80 km、100 km 时系统的纠错译码. 在不同的信道传输距离下, 首先可计算得到相应的信道透射率T, 然后基于前文所述方法, 可以获得相应的安全码率与随调制方差的变化曲线, 如图6 所示.

从图6 的曲线可以看出, 针对不同传输距离以及相应的纠错矩阵, 都可以依据本文所提出的方案得到系统安全码率随调制方差变化的曲线, 并且均可求解得到使系统安全码率最大化的最优调制方差; 针对同一纠错矩阵下, 在其适用的传输距离范围内, 最优调制方差的大小随传输距离的增加而增加, 且与之对应的最大安全码率随着传输距离的增加而减小; 不同传输距离对应的最优纠错矩阵不同, 其最优的调制方差范围也不同, 需要根据实际情况选择合适的纠错矩阵来确定最优调制方差. 其次, 对于确定的传输距离,调制方差的调节范围较大, 可以采用多种不同码率的纠错矩阵来实现纠错译码, 基于本文所提出的方案可以从备选的纠错矩阵中选择出使系统安全码率最大化的纠错矩阵以及与之对应的最优调制方差. 这一优化方案, 将CV-QKD 系统的光电层参数调制和后处理层的纠错译码能力结合, 为系统的参数调节提供了依据. 通过定量分析协调效率和误帧率各自随调制方差的变化关系和制约特性, 综合得到系统安全码率与调制方差之间的函数关系式, 最终计算得到使系统安全码率最大化的最优调制方差, 进一步提升实际CV-QKD 系统的性能.

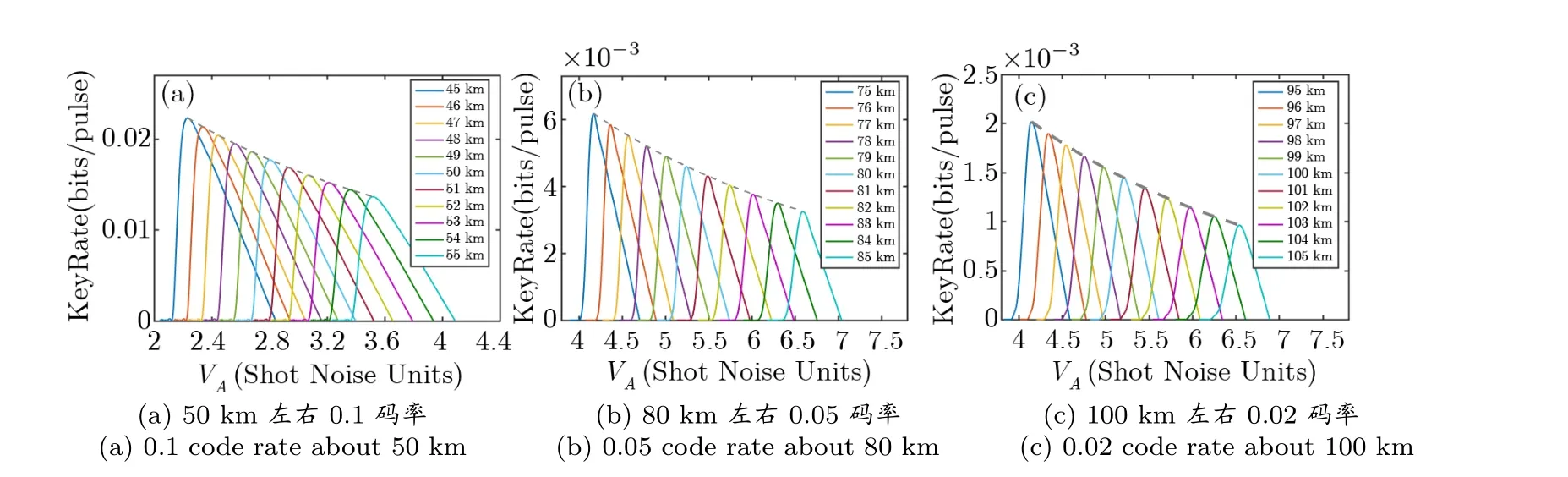
图6 安全码率和调制方差关系曲线Figure 6 KeyRate-VA curve

5 结论

本文提出了一种CV-QKD 协议调制方差全局优化方法. 对于确定的数据协商和纠错译码算法, 综合考虑了调制方差变化时协调效率和误帧率的变化特性, 量化分析了实际CV-QKD 系统中调制方差对误帧率、纠错效率等参数的影响, 以达到安全码率最大化. 相较于已知常用方法, 本优化方法在典型CV-QKD系统参数下仅通过调制方差参数优化即可将显著提升安全码率. 此外, 该方法适用于各类CV-QKD 协议,包括高斯调制、离散调制协议等, 也适用于有限码长和无限码长情形, 可扩展性好, 在今后的研究中将结合自适应译码或其他译码算法开展更加深入的研究.