一种高效的基于分治邻接表的动态完整性审计方案*
2021-09-14符庆晓陈兰香李继国姚志强
符庆晓, 陈兰香, 李继国, 姚志强
福建师范大学 计算机与网络空间安全学院 福建省网络安全与密码技术重点实验室, 福州350117
1 引言
随着云计算与云存储的广泛应用, 越来越多的单位及企业选择将其数据外包至云服务器. 源于云计算的规模经济效应, 可以为用户提供更加专业的数据存储与管理服务, 同时极大地节约经济成本与社会能源.当用户将数据存储到远程服务器, 便失去了对数据的物理控制权, 而云服务器往往并不完全可信. 数据外包特性及频繁爆发的数据安全事件, 使得用户对云存储服务的信心不足[1]. 因此需要一种数据完整性审计技术, 让用户可以随时随地验证其数据是否完整与可用. 由于数据拥有者无法存储外包数据的本地副本,所以传统的完整性验证在云计算中并不适用[2]. 为了解决云计算中外包数据的完整性审计问题, 研究者提出了远程数据完整性审计技术[3,4], 但现有的数据完整性验证方法需要频繁地进行审计和传输, 这样给审计者造成很大的计算和通信开销. 在支持外包数据动态更新方面, 现有的远程数据完整性审计方法采用不同的数据结构以支持数据动态更新, 比如二叉树、动态Hash 表等, 来证明外包数据的完整性, 但对于大文件中的少量数据块更新, 基于这些数据结构的验证算法需要重新平衡大量数据块, 会带来较大的计算开销[5]. 因此, 针对一些需要频繁更新的数据, 需要设计专门的数据完整性审计方法.
近年来, 针对云存储环境下的数据完整性审计已经取得了丰硕的研究成果, 也有大量针对数据动态性的研究方案, 但仍然存在诸如安全与效率的平衡、数据的隐私保护以及实用性等几方面的问题, 下面本文将介绍相关的研究工作.
2 相关工作
2007 年, Ateniese 等[6]最早提出可证明数据持有(provable data possession, PDP) 方案, 该方案使用同态标签来验证外包数据完整性. 随着云计算与云存储技术的广泛应用, 验证外包数据完整性得到研究者的广泛关注并取得了一系列的研究成果. 鉴于用户将数据存储到远程云存储服务器后, 通常有数据更新的需求, 因此, 研究者们提出了支持数据动态更新的完整性审计方案.
为了支持外包数据动态更新, 2008 年, Ateniese 等[7]提出了外包数据动态审计方案, 该方案在数据更新时, 让数据拥有者重新计算块标签, 因此会造成较大的计算开销. 2009 年, Erway 等[8]首次提出基于跳表的动态外包数据审计方案, 但是该方案不支持单个数据块的完整性验证, 而且数据块对应的验证路径较长. 2011 年, Wang 等[9]提出基于双线性聚合签名与Merkle 哈希树的动态审计方案, 该方案实现隐私保护公共审计和多用户环境下的批量验证. 然而, 该方案会造成外包数据审计时的数据泄露, 而对于云存储中大型外包数据文件也会带来较高的计算开销. 2015 年, 文献[10] 提出基于双线性对与Merkle 哈希树的云存储动态数据完整性审计方案, 该方案通过将数据块分割成长度更小的数据块, 使得Merkle 哈希树的每个叶子节点对应多个数据块, 从而有效降低Merkle 哈希树的高度, 但是该方案在数据初始化阶段的计算开销较大.
为了减少审计过程中的计算开销, 文献[11] 提出基于代数签名(algebraic signature) 的数据完整性验证方案, 可以显著降低外包数据审计过程中数据拥有者和云服务器的计算开销. 然而该方案无法支持外包数据的动态更新. 为支持动态数据更新,文献[12]提出基于Merkle 哈希树的云存储数据审计方案,但是因为Merkle 哈希树在数据更新时需要重新平衡二叉树, 造成较大的计算开销. 而且该方案在审计过程中, 数据拥有者需要对云存储中的外包数据进行完整性验证, 而不是授权给第三方审计者(third party auditor,TPA), 从而在外包数据审计过程中, 极大地增加了数据拥有者和云存储服务器的计算开销.
2014 年, 文献[13] 提出一个基于代数签名的云存储动态数据审计方案, 该方案引入了第三方审计者TPA, 减轻了审计过程中数据拥有者的计算开销, 并且提出索引表数据结构以支持数据动态更新, 但是该方案在数据更新时的效率比较低. 不久, 文献[14] 提出一个结合代数签名和分治表的动态数据审计方案,该方案使用代数签名对外包数据进行完整性审计, 同时提出分治表数据结构来支持数据的动态更新, 使得动态数据更新计算开销得到显著降低. 然而该方案使云存储服务器在不访问外包数据的情况下可以生成有效的证明, 从而容易造成审计过程中的数据隐私泄露并且容易受到重放攻击. 2018 年, 文献[15] 也提出一个结合代数签名和分治表的动态数据审计方案, 与文献[14] 不同的是, 该方案首先对数据块的索引号加密, 然后再生成块的校验值和块标记, 这样可以有效抵抗审计过程中的重放攻击和数据泄露问题. 然而该方案在审计过程中的初始化阶段会给数据拥有者造成过大的计算开销. 因此, 文献[16] 提出一个基于代数签名的数据完整性验证方案, 为了减少数据审计过程中数据拥有者的计算开销, 该方案引入第三方审计者, 将外包数据完整性审计授权给第三方审计者. 为了保护外包数据并防止审计过程中的数据隐私泄露问题, 他们还提出了异或同态函数(XOR-homomorphic function) , 可以一定程度上保护外包数据审计时所造成的隐私泄露问题. 最近, 韩静等[17]提出一种轻量级的支持用户可动态撤销及存储数据可动态更新的云审计方案, 利用多重单向代理重签名技术实现动态撤销, 引入虚拟索引实现实时动态更新. 文献[18] 利用Fisher-Yates Shuffles 算法构造异或同态函数, 使得算法的时间开销比较大, 时间复杂度为O(n2). 在支持外包数据更新方面, 他们设计了记录表(record table, RTable)数据结构以支持外包数据动态更新, 但删除或者插入数据块(i), 必须移动(n −1) 个数据块, 因此造成严重的计算负载.
为了解决数据动态更新过程中计算开销太大的问题, 本文设计一种新的分治邻接表(divide and conquer adjacency table, D&CAT) 数据结构实现高效的动态更新操作. 数据的基本审计方案基于代数签名, 为了保护审计过程中的数据隐私, 使用Knuth-Durstenfeld Shuffle 算法构造异或同态函数, 相比算法Fisher-Yates Shuffles 的O(n2), 根据文献[19] 洗牌算法证明, 该算法的时间复杂度O(n), 从而可以相应减少异或同态函数的时间开销. 分治邻接表结构在外包数据更新操作时, 当删除或者插入数据块(i)时, 只需要修改对应数据块的链表指针, 从而可以有效提高外包数据更新操作的效率.
下文结构组织如下: 第3 节介绍相关预备知识, 包括系统模型、代数签名与异或同态函数; 第4 节详细介绍本文提出的完整性审计方案; 第5 节对本方案的安全性与性能进行分析; 第6 节总结全文并指出下一步的研究工作.
3 预备知识
本节介绍系统模型、代数签名和异或同态函数的相关知识.
3.1 系统模型
本文提出方案的系统模型包括3 个实体: 数据拥有者, 云存储服务器, 第三方审计者. 其系统模型如图1 所示.
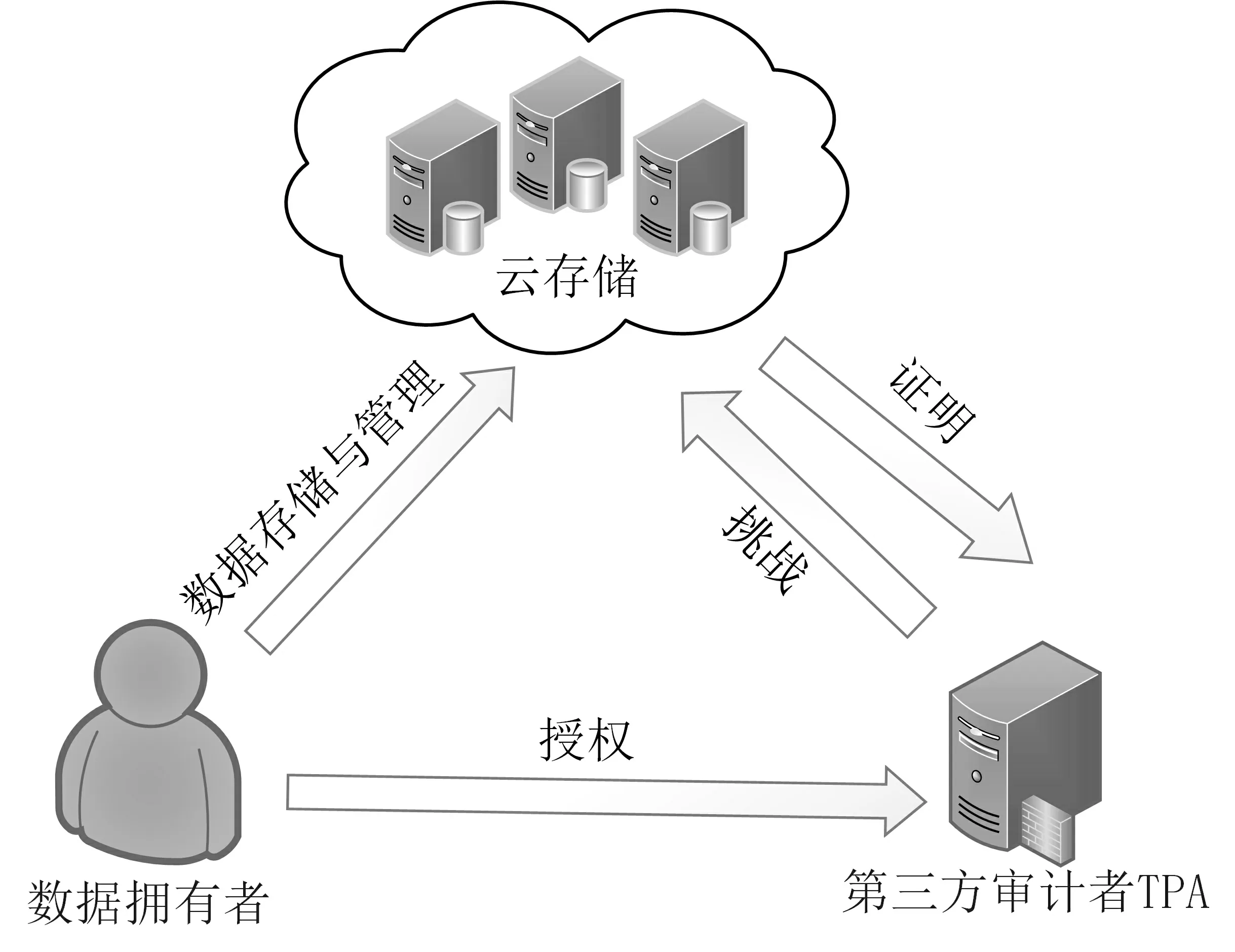
图1 外包数据审计流程Figure 1 System model
(1) 数据拥有者(data owner, DO): 指将数据存储在云存储服务器中的企业或个人, 他们拥有修改、插入、删除权限来更新外包数据.
(2) 云存储服务提供者(cloud storage provider, CSP): 负责存储数据拥有者的数据并生成验证证据作为对用户挑战的响应.
(3) 第三方审计者(third party auditor, TPA): 审计外包数据并进行完整性验证.
3.2 代数签名
代数签名(algebraic signature) 是一种具有同态性的哈希函数, 用于为文件块生成同态标签. 代数签名的代数性质是指数据块的代数签名之和与相应数据块之和的代数签名相同. 由n个数据块(F[1],F[2],··· ,F[n]) 组成的文件F的代数签名计算如下:
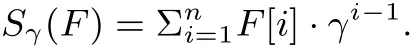
其中,γ为有限域的本原元素, 代数签名有以下3 个性质:
性质1: 长度为r的数据块F[I] 和F[j] 相连接的代数签名计算公式为
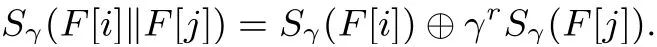
性质2: 文件F的所有数据块之和的代数签名与每个数据块代数签名之和相等:
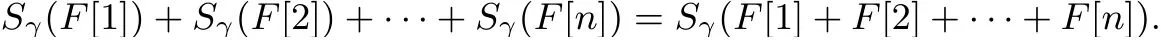
性质3: 文件F与文件G之和的代数签名与各个代数签名之和相等:
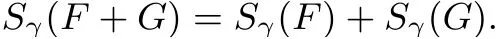
3.3 异或同态函数
异或同态函数(XOR-homomorphic function) 是指具有异或同态特性的伪随机函数, 它可以增强对数据的隐私保护. 异或同态函数f有以下相应的性质:
性质4: 对输入x1,x2的异或运算等于函数f对每个输入的异或运算:
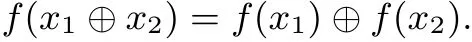
性质5: 对于置换密钥(k1,k2), 则:
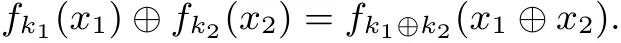
3.4 威胁模型
当DO 将数据外包到云存储中, 并将数据委托给CSP 时, 数据的完整性可能面临以下风险:
(1) 由于硬件或管理错误, 以及各种内部或外部攻击, CSP 有可能隐藏外包数据丢失或受损情况.
(2) 为了节省资源, CSP 可能会忽略执行数据所有者要求的数据更新操作. 例如, 在挑战验证阶段, 不诚实的CSP 可能利用以前的合法响应或其他信息生成证明, 而不需要检索实际外包数据, 以欺骗TPA 通过验证(重放攻击) .
针对以上问题, 本文提出一种通过验证外包数据的完整性来检测CSP 不当行为的方法.
4 方案详细设计
本节首先对方案的几个算法进行形式化描述, 然后对每个算法进行详细介绍.
4.1 算法形式化描述
本文提出的动态数据完整性审计方案包括两个部分: 基本的完整性审计方案与动态数据更新方案. 基本的完整性审计方案分为4 个阶段: 初始化阶段、挑战阶段、回应阶段与验证阶段, 包括5 个多项式时间算法; 动态数据更新方案包括4 个多项式时间算法. 算法的形式化定义如下.
• Setup (1λ)→(params,sk) : DO 使用Setup 算法以安全参数λ为输入, 随机输出公共参数params 和密钥sk.
• TagGen(params,sk,F)→(T) : DO 使用TagGen 算法, 以公共参数params、密钥sk、文件F为输入, 输出每个数据块的标签Ti.
• Challenge (c)→(chal) : TPA 使用Challenge 算法随机输出挑战消息chal.
• Response(params,F,Ti,chal)→(proof): CSP 使用Response 算法, 以公共参数params、外包文件F、挑战消息chal 以及对应挑战块的标签为输入, 输出回应消息proof.
• Verify(params,sk,chal,proof)→(1,0): TPA 使用Verify 算法, 以公共参params、密钥sk 和回应消息proof 作为输入, 输出结果1 或0.
动态数据更新方案的4 个多项式时间算法的形式化定义如下.

4.2 算法详细设计
上节对本方案的算法进行了形式化描述, 下面将对以上算法的详细过程进行描述.4.2.1 基本的完整性审计
基本的完整性审计方案分为4 个阶段: 初始化阶段、挑战阶段、回应阶段与验证阶段, 包括5 个多项式时间算法, 分别详述如下, 其流程如图2 所示.
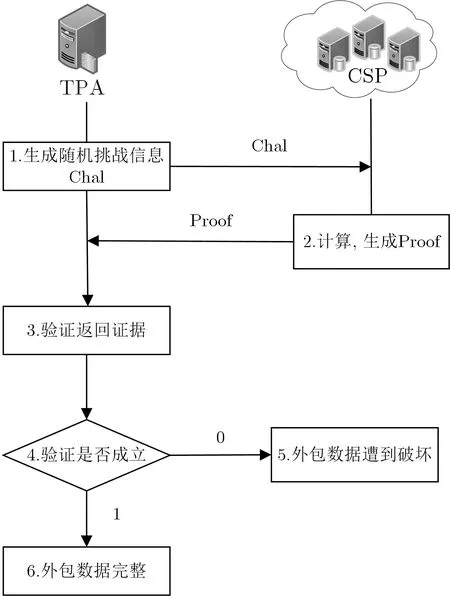
图2 外包数据审计流程Figure 2 Audit processs
(1) 初始化算法Setup(1λ)→(params,sk) 的执行过程如下.
(1.1) 数据拥有者DO 首先通过数据分片技术将文件F分为n个数据块F[1],F[2],··· ,F[n].

云存储服务器CSP 接收到TPA 的挑战消息chal 后执行以下计算:
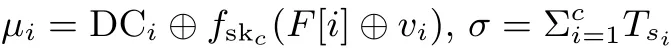

(5) 验证算法Verify(params,sk,chal,Proof)→(1,0) 的执行过程如下.
当TPA 接收到CSP 发送的Proof 消息时, TPA 首先计算TCi=fskt(τi ⊕vi), 然后计算ωi=µi ⊕TCi, 此后TPA 可以通过以下等式验证外包数据块的完整性:
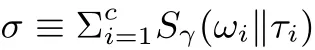
其正确性证明如下:


4.2.2 基于分治邻接表的动态数据更新
动态数据更新是数据完整性审计中的一个非常重要的特征, 实现不用下载数据情况下的外包数据的更新. 尽管文献[16] 提出的RTable 数据结构可以支持动态数据更新. 但插入一个数据块需要完成(n −1)次数据块移动. 为了更好地支持动态数据更新, 本文提出分治邻接表数据结构, 在删除或者插入数据块(i) 时, 只需要修改对应数据块的链表指针, 不需要移动之后的数据块, 同时, 根据表头结点的LMIN 与LMAX 可以快速定位结点, 从而可以较好地提高外包数据更新操作的效率.
分治邻接表主要由两个数据结构组成: 表头数组与链表. 表头数组的每个结点由四个部分构成:LMIN 表示对应链表最小的数据块的索引号, LMAX 表示为对应链表最大的数据块的索引号, FIRST表示对应链表的头指针, REAR 表示对应链表最后一个结点指针. 链表则由三个部分构成: LN 表示数据块的索引号, TIME 表示数据块最后更新的时间, NEXT 表示下一个结点的指针. 同时为了表述方便, 使用MAX 表示文件最大的逻辑索引号.
数据拥有者DO 在上传外包数据到CSP 之前, 为每个文件生成对应的D&CAT 数据结构. 为了实现数据的动态更新, 我们设计了数据修改Modify、数据插入Insert、数据附加Add 与数据删除Delete 等4个数据更新算法.

假设DO 需要修数据块F[2], 则修改前的分治邻接表如图3 所示.
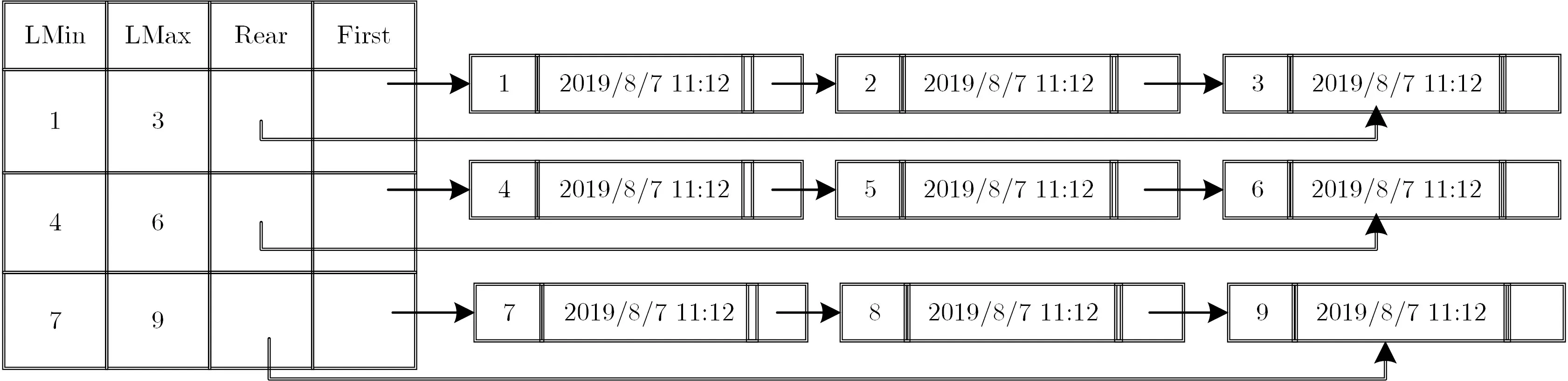
图3 数据修改前的分治邻接表Figure 3 D&CAT before modification
当修改完成后, 分治邻接表如图4 所示.
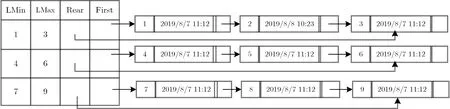
图4 数据修改后的分治邻接表Figure 4 D&CAT after modification

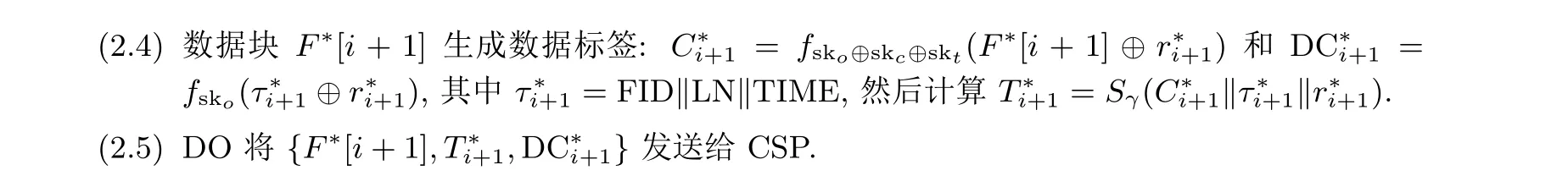
假设DO 需要在数据块F[2] 后插入一个新的数据块, 设新数据块插入前的分治邻接表如图4 所示. 而当新数据块插入完成后, 其分治邻接表如图5 所示.

图5 插入数据块后的分治邻接表Figure 5 D&CAT after inserting
(3) 数据附加算法Add(F[n+1])→(Tn+1,DCn+1,Noden+1) 的执行过程如下.假设DO 需要将新的数据块F[n+1] 附加到文件F后面, 则DO 将会执行以下操作:
(3.1) 找到表头结点的最后一个结点.
(3.2) 创建一个新的链表结点Noden+1, 即LN=MAX,TIME=TIMEn+1, 其中TIMEn+1为当前时间, NEXT=∧.
(3.3) 修改表头结点的LMAX = LMAX+1, 将对应链表最后一个结点域NEXTrear指向新创建的链表结点, 然后将REAR 指向新建的结点Noden+1.
(3.4) 计算Cn+1=fsko⊕skc⊕skt(F[n+1]⊕rn+1) 和DCn+1=fsko(τn+1⊕rn+1), 其中τn+1=FID‖LN‖TIME, 然后计算Tn+1=Sγ(Cn+1‖τn+1‖rn+1).
(3.5) DO 将{F[n+1],Tn+1,DCn+1}发送给CSP.
假设DO 在文件F附加一个新的数据块, 设新数据块附加前的分治邻接表如图5 所示. 而新数据块附加完成后, 其分治邻接表如图6 所示.

图6 附加新数据块后的分治邻接表Figure 6 D&CAT after adding
(4) 数据删除算法Delete(i)→(1,0) 的执行过程如下.
假设DO 需要将数据块F[i] 删除, 则DO 将会执行以下操作:
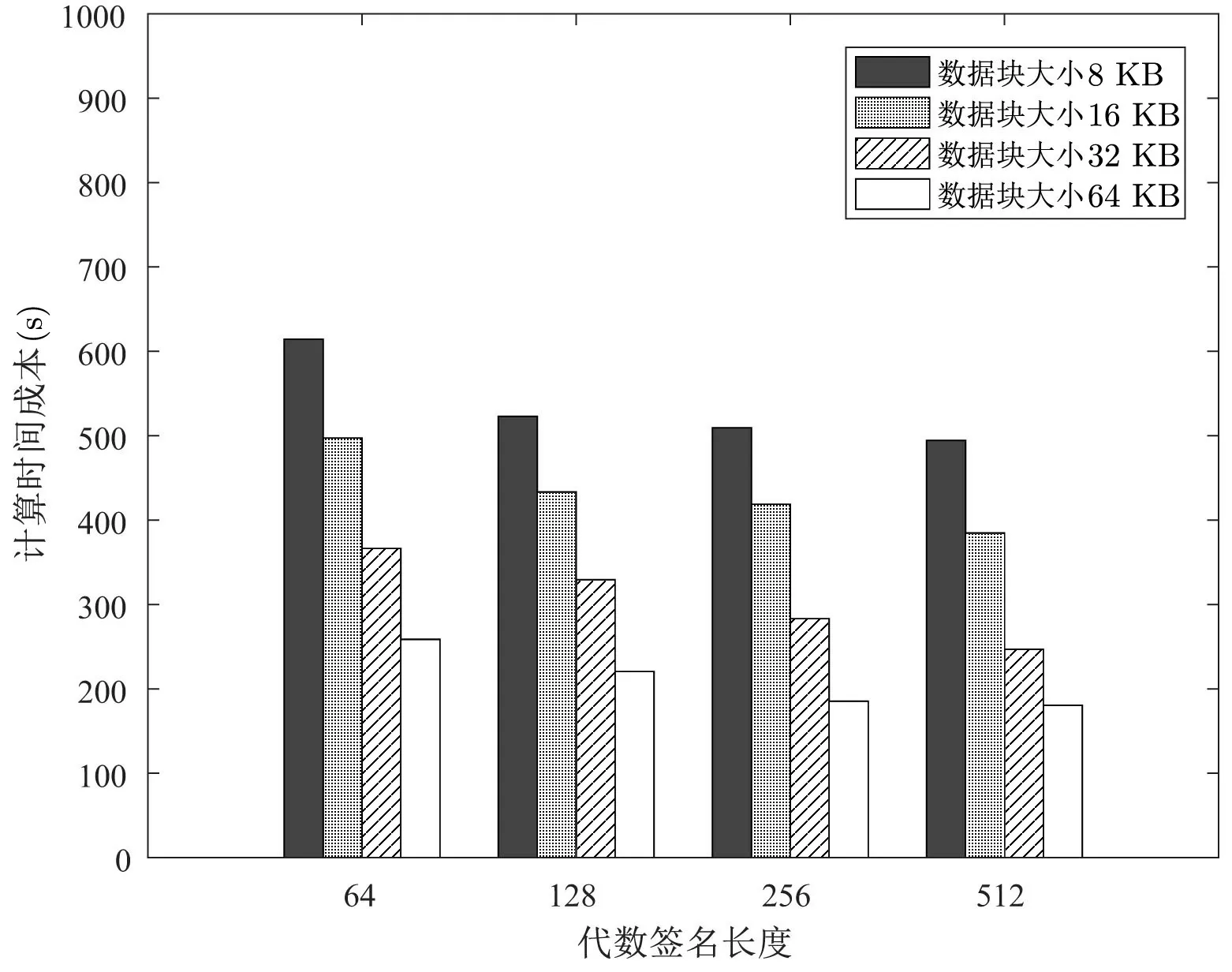
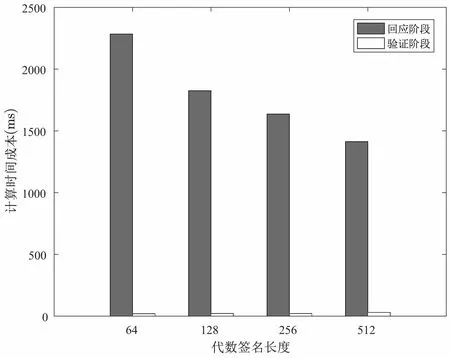
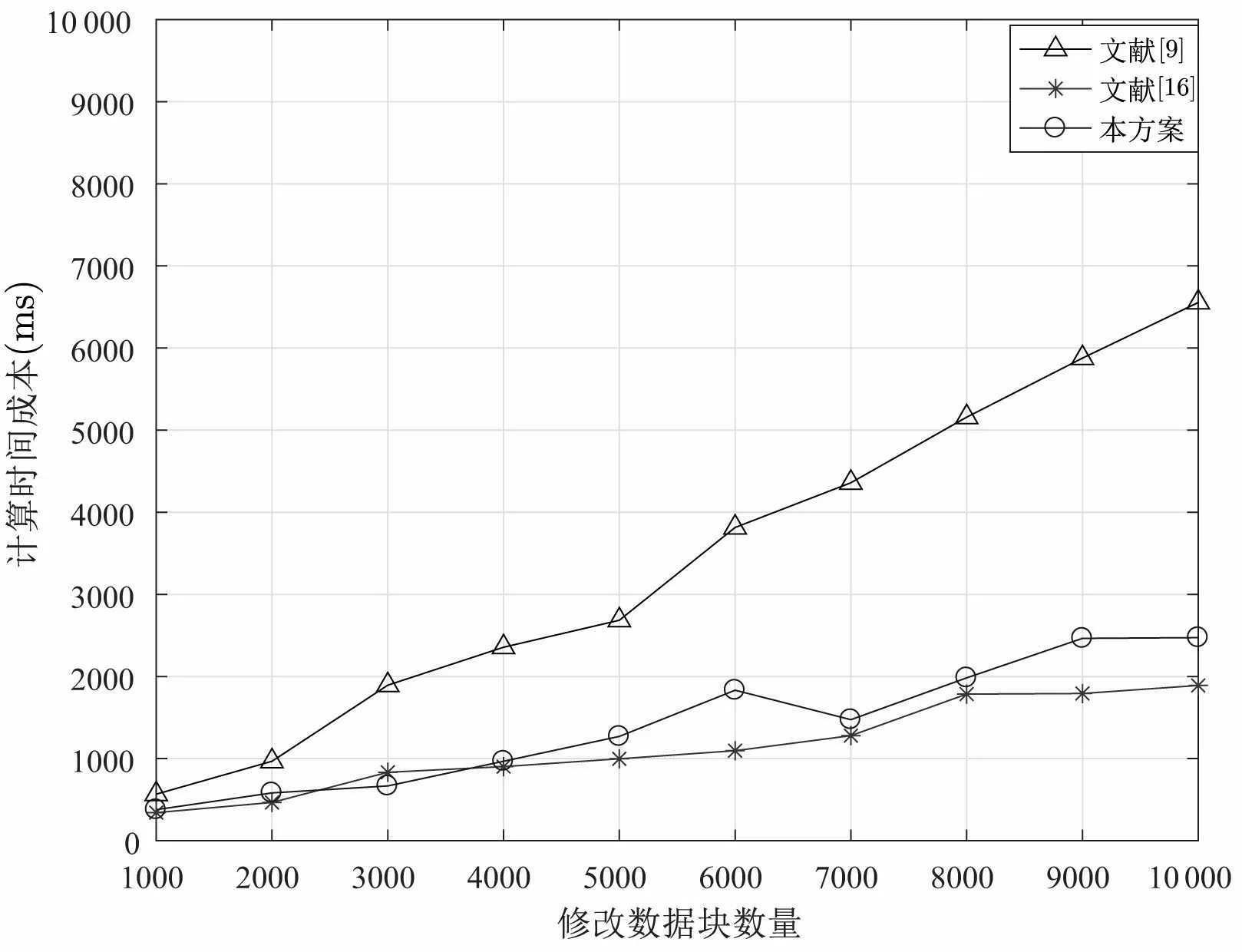
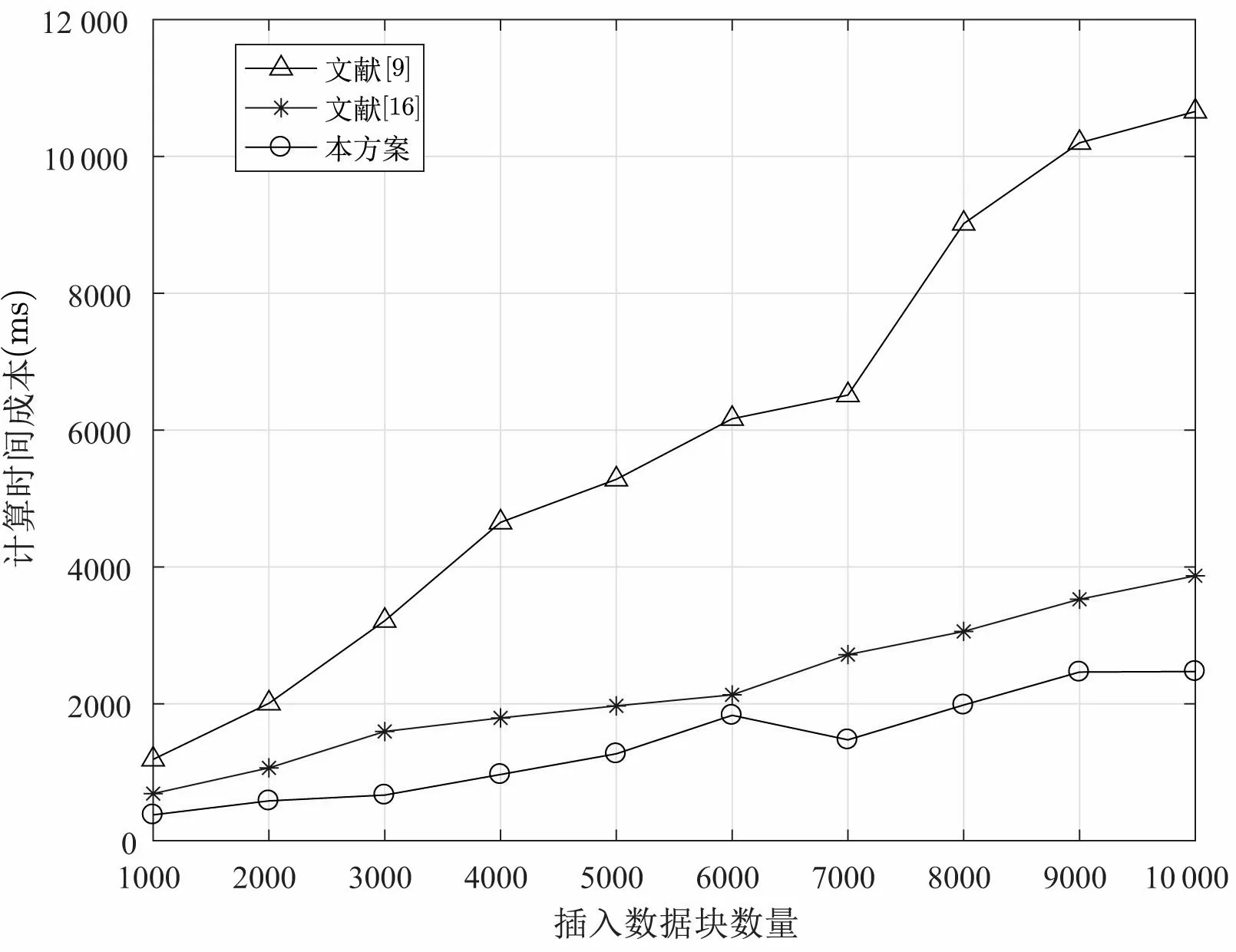
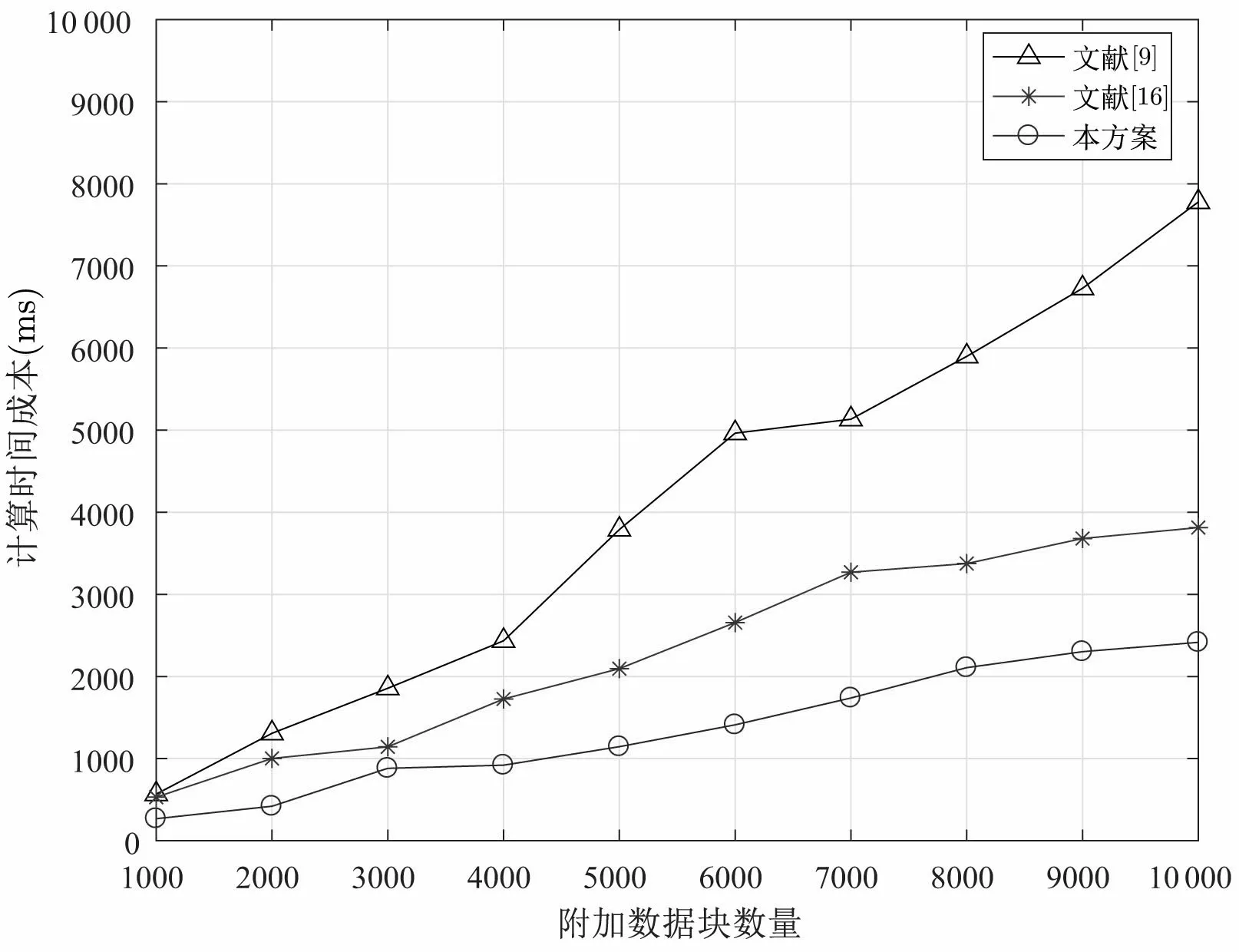
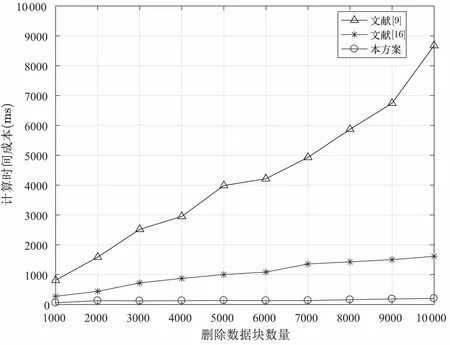
(4.1) 根据F[i] 查找表头数组, 若满足LMIN (4.2) 若第i个数据块对应结点为链表第一个结点, 则将表头结点域FIRST = NEXTi. 若第i个数据块对应结点为链表最后结点, 则直接将表头结点域REAR 指向第i −1 个结点. 若第i个数据块既不是链表对应第一个结点和最后结点, 则将第i −1 对应的结点中NEXTi−1=NEXTi, 相应表头结点LMAX 以及随后表头结点中LMIN 和LMAX 均减1. (4.3) CSP 删除对应数据块, 删除完成后, CSP 返回1, 否则返回0. 假设DO 需要删除数据块F[2], 设删除数据块前的分治邻接表如图6 所示. 在删除数据块完成后,其邻接表如图7 所示. 图7 删除数据块后的分治邻接表Figure 7 D&CAT after deleting 本节对方案的安全性与性能进行分析. 本方案的核心是对存储在云服务器上的数据执行完整性审计, 而且由可信第三方审计者TPA 代替数据拥有者进行不定期审计. 关于数据的机密性与访问控制不在本文的讨论范围, 而且在实际系统中, 数据可以加密存储, 本方案仍然适用于作加密数据的完整性验证. 在系统模型三方之间的相互认证可以使用已有的认证机制, 相互的通信可以使用保密信道, 比如SSL/TLS. 这里的安全性分析主要考虑的是数据完整性审计方案及动态更新过程中的安全问题, 包括代数签名的鲁棒性与异或同态函数的安全性, 本方案中代数签名可取足够长的签名长度, 碰撞概率是非常低的, 甚至可以忽略不计. 一个128 bits 的签名可能发生的碰撞概率为2−128, 一个256 bits 的代数签名可能发生的碰撞概率则为2−256, 同时代数签名的计算效率非常高. 在保护数据隐私泄露方面, 方案使用Knuth-Durstenfeld Shuffle 算法构造异或同态函数生成随机校验值, 使得TPA 将无法在审计外包数据时获取任何关于用户的信息, 却可以审计外包数据完整性. 同时, 因为本方案支持外包数据动态更新, 所以当更新数据块时, 也需要相应更新对应的数据块的标签. 然而, 不诚实CSP 有可能不响应DO 更新外包数据请求. 所以CSP 可能利用过期的版本的外包数据块和标签欺骗TPA. 为此, 为了抵抗重放攻击方面, 假设DO 请求CSP 更新外包数据, 如果CSP 忽略外包数据更新请求, 并在TPA 审计数据时发送旧的数据标签, 这时TPA 可以检测到CSP 的行为. 这是因为分治邻接表数据结构中的参数TIME 记录每个数据块相应更新时间, 并嵌入对应数据块标签中即是τi=FID‖LN‖TIME,Ti=Sγ(Ci‖τi), 所以重放的标签不能以一个不可忽略的概率通过TPA 的验证. 本文方案相比于文献[16], 一方面是使用分治邻接表数据结构替代记录表数据结构来实现更加高效的数据更新. 另一方面利用Knuth-Durstenfeld Shuffle 算法[18]构造异或同态函数, 实现时间复杂度从Fisher-Yates Shuffles 算法的O(n2) 下降至O(n). 关于本文方案的形式化安全性证明可以参考文献[16]. 本方案的外包数据验证采用随机抽样策略, 外包数据篡改检测的概率是基于数据块抽样. 即将文件F分为n个数据块, 并随机选择c个数据块作为一个质询检测, 下面对外包数据篡改检测概率进行分析. 所以可得外包数据篡改检测的概率范围为: 假设DO 将1 GB 文件划分为125 000 个数据块, 则每个数据块为8 KB, 然后将数据上传至CSP,若PX= 0.9 以及PX= 0.999 99 的概率检测到外包数据篡改时, 不同数量的篡改数据块与挑战数据块的关系如图8 所示. 由图8 可知, 若要TPA 检测概率达到PX= 0.9, 当CSP 篡改数据块比例为10% 时, 则至少需要挑战质询的数据块个数为22 块; 若要TPA 检测概率达到PX=0.95, 且在CSP 篡改数据块比例为10% 条件下, 则需要挑战质询的数据块个数为30 块; 若要TPA 检测概率达到PX=0.97 在同样条件下, 则至少需要挑战的数据块个数为35 块; 若要TPA 检测概率达到PX= 0.999 99, 则至少需要质询的数据块个数为110 块. 关于外包数据完整性审计方案的存储开销与通信开销, 大部分方案都是相似的, 因此本文主要从计算开销, 即方案的计算效率方面进行分析. 实验利用一台配置为Intel Core i5-8250U CPU @ 1.6 GHz CPU 以及8 GB RAM 的PC 机, 采用Eclipse 集成开发工具并使用Java 语言实现本文方案与文献[9,16] 方案中的数据审计与动态更新算法. 本方案的性能分析主要包括两个方面: (1) 基本审计方案的时间开销: 包括初始化阶段, DO 用于生成文件块标签的计算开销; 响应阶段CSP 生成证据的计算开销; 验证阶段, TPA 验证外包数据块完整性的计算开销. (2) 动态更新方案的时间开销: DO 对外包数据执行修改、插入、附加和删除更新操作所需计算开销. 为了分析基本审计方案中代数签名长度和数据块大小对初始化阶段时间开销的影响, 我们选取5 GB的文件, 分别将外包文件的数据块分为8 KB、16 KB、32 KB、64 KB, 并依次选取代数签名长度为64、128、256 及512 bits, 分析实验中初始化阶段的时间开销, 实验的结果取10 次测试结果的平均值, 其时间开销如图9 所示. 图9 初始化阶段时间开销Figure 9 Time overhead of setup phase 由图9 可知, 在代数签名长度相同的情况下, 随着数据分块大小的增加, 初始化阶段计算开销减少. 在数据块大小相同情况下, 随着代数签名长度的增加, 初始化阶段时间开销也相应减少. 实验结果表明, 随着代数签名长度和数据分块增加, 初始化阶段的开销相应减少, 其原因是签名长度长, 分块粒度大, 减少分块数量, 从而减少计算时间. 我们设定将外包文件的数据块分为8 KB, 挑战外包数据块数为5000, 并依次选取代数签名长度为依次选取代数签名长度为128、256 及512 bits, 分析实验中回应阶段和验证阶段的时间开销, 实验的结果取10 次测试结果的平均值, 时间开销如图10 所示. 图10 回应阶段和验证阶段时间开销Figure 10 Time overhead of response and verification phase 由图10 所示可知, 在数据分块大小为8 KB 情况下, 随着代数签名长度的增加, 回应阶段时间开销也相应减少. 然而, 即使代数签名长度增加, 验证阶段的时间开销始终大约在25 ms 左右. 实验结果表明, 随着代数签名的增加, 响应阶段的时间开销降低. 为了测试动态更新方案的时间开销, 我们将本文所提方案与文献[9,16] 提出的方案从数据修改、插入、附加与删除操作进行比较. 选取5 GB 的文件, 设分块大小为8 KB, 代数签名长度为512 bits, 更新数据块数量从1000 到10 000 递增, 每次更新数据块随机抽取. 数据修改操作的实验结果如图11 所示. 图11 不同数据块数的修改时间开销Figure 11 Modification time overhead of different number of blocks 与文献[16] 相比, 当修改数据块数小于5000 时, 两方案的时间开销是相似的, 但当修改数据块数继续增加时, 本方案的时间开销高于文献[16] 方案的开销. 由于文献[16] 方案采用RTable 数据结构, 在查找数据块时速度比较快, 所以在修改数据块时优于本文所提方案. 与文献[9] 相比, 本文方案与文献[16] 方案的数据修改效率均较高. 数据插入操作的时间开销如图12 所示, 文献[9] 提出的动态数据插入操作需要重新调整Merkle 树,所以会造成较大的计算开销. 文献[16] 提出的动态数据插入方案在插入数据块F[i] 时, 需要(n −i) 次数据块移动操作, 因此会造成较大的时间开销. 而在本文所提方案中, 插入数据块F[i] 只需要修改对应的指针, 即只需移动1 次, 从而可以极大地降低插入操作的时间开销. 实验结果表明本文所提出方案可以显著降低插入数据的计算开销. 图12 不同数据块数的插入时间开销Figure 12 Inserting time overhead of different number of blocks 数据附加操作的时间开销如图13 所示, 文献[9] 提出的动态数据附加方案需要重新调整Merkle 树,因此有较高的计算开销. 在文献[16] 提出的动态数据附加方案中, 当附加数据块F[n+ 1] 时, 需要将RTable 表的长度由n增加为n+1, 此操作的时间开销较大. 而在本文所提方案中, 附加数据块F[n+1]只需将rear 指针指向新的附加数据块, 因此本文方案的附加操作可以显著降低计算开销. 图13 附加不同数据块数的时间开销Figure 13 Addition time overhead of different number of blocks 数据删除操作的时间开销如图14 所示, 删除操作与插入操作正好相反, 即删除数据块F[i] 时, 文献[16] 提出的动态数据删除操作需要移动(n −i) 次数据块; 文献[9] 删除数据块时与动态插入数据一样,需要动态调整Merkle 树, 因此它们的计算开销均较大. 本文所提方案只需更改对应的指针, 即只需移动1次, 所以本文所提出方案删除操作可以显著地降低计算开销. 图14 删除不同数据块数的时间开销Figure 14 Deleting time overhead of different number of blocks 表1 主要分析文献[9,16] 与本方案的外包数据更新的计算开销对比, 其中n代表外包数据块个数,c代表更新的外包数据块个数. 表1 不同方案的数据更新操作对比Table 1 Comparison of data updating of different schemes 因此, 四种数据更新操作中, 文献[16] 只有修改操作的时间开销略低于本文方案, 其余三种更新操作,包括插入、附加与删除操作的时间开销都比本文方案高, 文献[9] 的四种更新操作的时间开销均是最大.总地来说, 本文方案的计算是最高效的. 本文提出一种高效的外包数据完整性验证方案, 采用代数签名验证外包数据的完整性, 为了防止审计时造成数据隐私泄露问题, 引入了异或同态函数. 同时为了更好地支持外包数据的动态更新操作, 我们设计出一种分治邻接表数据结构提供更加高效的数据更新. 实验结果表明本文方案的可行性和高效性. 下一步工作中, 我们将在此基础上通过运用轻量级加密技术, 实现更加有效防止外包数据泄露的方法, 同时希望将本方案进一步扩展, 用于分布式云存储系统.
5 安全性与性能分析
5.1 安全性分析
5.2 篡改概率分析

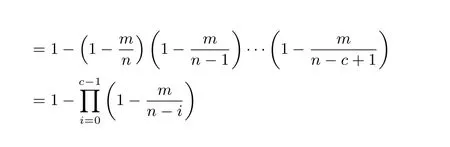
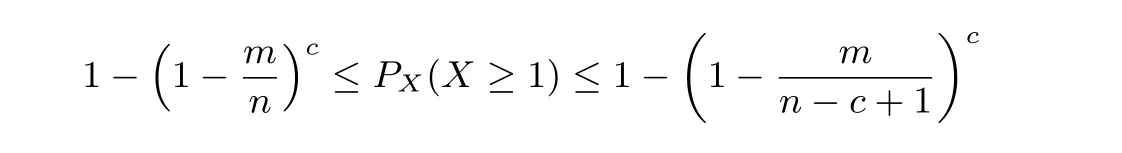
5.3 性能分析

6 结论与未来研究
