强差族及其在相对差族、可分组设计和光正交码中的应用

杨凯璐,王小苗

（宁波大学 数学与统计学院,浙江 宁波 315211）

组合设计是组合数学的一个重要分支,主要研究各种离散结构的存在性和构造性、分类和计数问题等.近几十年来,组合设计在通信技术和信息安全领域发挥了重要作用.作为相对差集的自然推广,相对差族在1998 年由Buratti[1]提出.相对差族是构造组合设计的强有力工具,在研究光正交码、光正交签名码方面具有重要应用.

由于相对差族的研究缺乏系统的构造方法,1999 年Buratti[2]首次提出了强差族概念.此后近10 年对强差族的研究进展十分缓慢,直到2008 年,Buratti 等[3]讨论了任意图上的强差族,推广了任意图上恰顶点可迁的完全多部图的图分解.并建立了二面体群上的强差族,从而得到了一类可分组设计.Momihara[4]构造了循环强差族的无穷类,同时给出了特殊参数强差族的不存在性证明.此外,借助平方和思想,完全解决了二阶循环群上区组大小任意的强差族.Costa 等[5]借助强差族得到了框架差族,即对应于可分解的循环相对差族.Bao等[6]指出,可分解的循环相对差族是构造严格最优跳频序列的重要工具,跳频多址系统在现代通信系统,如超宽带、军事通信等方面有广泛应用.Buratti[7]通过引入哈达玛强差族得到了可划分差族.Ding等[8]利用可划分差族构造了最优常重复合码,后者在电力线通信的多进制数字频率调制中应用广泛.关于强差族的相关成果,还可参见文献[9-12].

本研究得到了循环群上强差族的新的结果,并构造了相对差族的渐近存在和离散例子,且利用相对差族扩大了可分组设计的存在性,最后给出了组合设计理论在最优光正交码上的应用.

1 预备知识

在全文中,集合和多重集分别用大括号{}和方括号[]表示,每个并集指保留元素重数的多重集的并.A∪A∪…∪A(h次)用hA表示.

令(G,+)是一个有限群,其中恒等元记作0.令K= [k1,k2,…,ks]为正整数的集合,Σ= [F1,F2,…,Fs]是G的多重集构成的集族,其中Fi=[f i,1,fi,2,…,fi,ki],1≤i≤s.若满足条件:

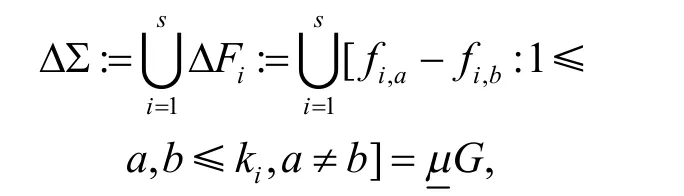
即G中每个元素(包括0)在多重集ΔΣ 中恰出现μ次,则Σ 称为一个(G,K,μ)-强差族(SDF).Σ 中元素称为基区组.显然,.值得注意的是,由于元素0∊G在任意多重集中作为差总是出现偶数次,故μ一定是偶数.若每个基区组的大小均为k,则简记为(G,k,μ)-SDF.

命题1若存在一个(G,k,μ)-SDF,则μ为偶数且μ|G| ≡ 0(modk(k-1)).

对于正整数r和基区组B,令表示B在基区组的集合中出现r次.

引理 1[12]当(v,k,μ) ∊{(56,8,4),(56,8,6),(72,9,4)}时,存在一个(Zv,k,μ)-SDF 为:

一个(G,N,k,λ)相对差族(DF),或含有n阶子群N的g阶群(G,+)上的(g,n,k,λ) -DF 是指G的k-元子集构成的集族 B= [B1,B2,…,Br](基区组),使得:

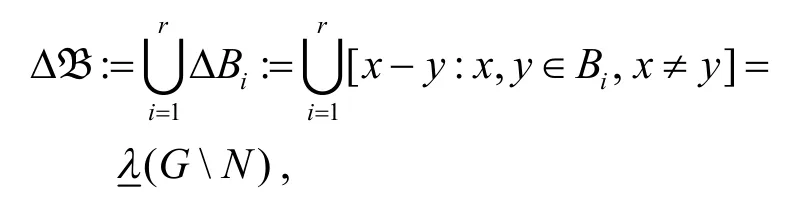
即,GN中的每个元素在多重集ΔB 中恰出现λ次,且N中的元素在ΔB中不出现.若G是循环群,称(g,n,k,λ)-DF 是循环的.

2 强差族和相对差族

3 组型为(k (k- 1))u的k-可分组设计

相对差族可以用来构造可分组设计.令K为正整数的集合.一个可分组设计(GDD)K-GDD是指一个三元组(X,G,A),满足性质:(1)G 是有限集X的一个划分(称为组);(2)A 是X中大小取自K的子集构成的集合(称为区组),使得X的每个2-子集恰包含在一个区组中或恰包含在一个组中,但不能同时包含在区组和组中.若G 含有ui个大小为gi的组,其中1≤i≤r,则称为GDD 的组型.当K={k}时,简记为k-GDD.

引理6

(1)当u∊{6,16,21,25,26,36,41,42,48,49,51,66,71,76,78,81,84,85,86,90,91,96} ∪{q:q≡1(mod6)是素数}时,存在一个组型为30u的6-GDD[10].

(2)当u∊{7,8,9,15,17,28,33,36,41,49,50,56,57,63,64,65,70,71,72,73,77,78,80,81,85,88,91,92,96,97,99}时,存在一个组型为42u的7-GDD[13].

(3)当u∊{8,9,10,15,16,17,29,30,33,36,37,41,43,44,49,50,51,53,54,55,57,58,63,64,65,71,72,73,74}∪[79,99]时,存在一个组型为56u的8-GDD[13].

(4)当u∊{9,10,17,19,49,54,55,57,58,64,65,66,73,74,80,81,89,90,91}时,存在一个组型为72u的9-GDD[13].

引理7当素数q≡ 5(mod8)且q﹥ 13时,存在一个组型为30q的6-GDD.

证明由定理2 知,当素数q≡ 5(mod8)且q﹥ 13时,存在一个(Z30× Fq,Z30×{0},6,1)-DF.由Z30×Fq上该DF的基区组可生成组型为30q的6-GDD.

结合引理6 中(1)和引理7,得到以下定理.

定理7当u∊{6,16,21,25,26,36,41,42,48,49,51,66,71,76,78,81,84,85,86,90,91,96} ∪{q:q﹥5,q≡ 1,5,7,13,19(mod24)是素数}时,存在一个组型为30u的6-GDD.

引理8当素数q≡ 5(mod8)且q﹥ 13时,存在一个组型为42q的7-GDD.

证明由定理3 知,当素数q≡ 5(mod8)且q﹥ 13时,存在一个 (Z42× Fq,Z42×{0},7,1)-DF.由Z42× Fq上该DF 的基区组可生成组型为42q的7-GDD.

结合引理6 中(2)和引理8,得到以下定理.

定理8当u∊{7,8,9,15,17,28,33,36,41,49,50,56,57,63,64,65,70,71,72,73,77,78,80,81,85,88,91,92,96,97,99}∪{q:q﹥ 13,q≡ 5(mod8)是素数}时,存在一个组型为42u的7-GDD.

引理9当素数q≡ 1(mod4)且q﹥Q(4,7),或q≡ 7(mod12)且q﹥Q(6,7)时,存在一个组型为56q的8-GDD.

证明由定理5 知,当素数q≡ 1(mod4)且q﹥Q(4,7),或q≡ 7(mod12)且q﹥Q(6,7)时,存在一个(Z56×Fq,Z56×{0},8,1)-DF.由Z56× Fq上该DF的基区组可生成组型为56q的8-GDD.

定理9当u∊{8,9,10,15,16,17,29,30,33,36,37,41,43,44,49,50,51,53,54,55,57,58,61,63,64,65,67,71,72,73,74}∪[79,99] ∪{q:q﹥4848812032,q≡ 1(mod4)是素 数} ∪{q:q﹥ 1830677303808,q≡ 7(mod12)是素数}时,存在一个组型为56u的8-GDD.

证明由引理4 知,当u∊ { 61,67}时,存在一个(Z56×Fu,Z56×{0},8,1)-DF,故由 Z56×Fu上该DF的基区组可生成组型为56u的 8-GDD.当u∉ { 61,67}时,由引理6 中(3)和引理9 可以得到组型为56u的 8-GDD,其中Q(4,7)=4848812032,Q（6,7）=1830677303808.

引理10令素数q≡ 5(mod8).当q﹥Q(4,8)或37 ≤q≤9 973时,存在一个组型为72q的9-GDD.

证明由定理 6 知,在 Z72× Fq上由(Z72×Fq,Z72×{0},9,1)-DF 的基区组可以生成一个组型为72q的9-GDD.

由于Q（4,8）= 107375099904,故结合引理6 中(4)和引理10 得到以下定理.

定理10当u∊{9,10,17,19,49,54,55,57,58,64,65,66,73,74,80,81,89,90,91} ∪{q:q∊ [ 37,9973]∪[107375099904,+∞),q≡ 5(mod8)是素数}时,存在一个组型为72u的9-GDD.

4 最优光正交码

利用定理2、3、5 和6 来构造最优光正交码.一个码重为k的(v,k,1)-光正交码(OOC)是指 Zv的一些k-元子集(称为码字)构成的集合,要求子集中的任意2 个元素做差,使得该集合产生的所有的差均不重复,称 Zv中不出现在这些差中的元素构成的集合为差剩余.若差剩余的大小为小于或等于k(k-1),则称该光正交码为最优的.

一个循环(gv,g,k,1)-DF 可被看作是一个(gv,k,1)-OOC,其中差剩余恰为{0,v,2v,…,(g-1)v}.

定理11(1)当素数q≡ 5(mod8)且q﹥ 13时,存在一个最优(k(k- 1)q,k,1)-OOC,其中k∊{ 6,7}.(2)当素数q≡1 (mod4)且q﹥Q(4,7),或q≡7(mod12)且q﹥Q(6,7)时,存在一个最优(56q,8,1)-OOC.(3)令素数q≡ 5(mod8),当q﹥Q(4,8)或37 ≤q≤9973时,存在一个最优(72q,9,1)-OOC.

证明若k(k-1)和q互素,则 Zk（k-1）×Zq同构于 Zk（k-1）q.由定理2、3、5 和6 知,存在一个循环(k(k- 1)q,k(k- 1),k,1)-DF,其中k∊{ 6,7,8,9}.故存在一个(k(k- 1)q,k,1)-OOC,其中差剩余为{0,q,2q,…,(k(k-1) -1)q}.由于差剩余的大小恰好等于k(k-1),因此得到的光正交码是最优的.