基于FDE-IRF的室内指纹定位方法

张雯涛，吴飞，朱海，通雁辉，陆雯霞

( 上海工程技术大学电子电气工程学院，上海 201620 )

0 引言

室内定位解决的是全球卫星导航系统(GNSS)信号弱、缺失的定位问题.在一些公共区域，如大型商场、地铁站、地下停车场和大型医院等，需要精确度高的位置定位服务[1]，因此，提高室内定位精度的需求变得日益迫切.许多室内定位技术已经成为研究热点，主要包括超宽带(UWB)、蓝牙、射频(RF)、Wi-Fi、地磁和行人航迹推算[2].随着无线局域网(WLAN)在大范围内大量覆盖，基于Wi-Fi 的定位方法因其具有无需额外部署硬件设备且成本低的优势得到广泛应用[3-4].

基于接收信号强度(RSS)的室内定位技术[5]是目前最常用的方法，主要分为两种：基于距离衰减模型的三边法和基于指纹图谱的指纹法[6].基于指纹图谱的定位方法不需要知道无线访问接入点(AP)位置和信号衰减模型，是常用的RSS位置匹配方法[7].指纹识别方法通常包括两个阶段：离线训练和在线匹配.在离线训练阶段，构建可靠稳定的指纹库通常需要在同一参考点(RP)不同时刻反复采集指纹样本.随着待定位区间增大，采样过程耗费大量的时间和人力[8-9].为减少指纹库构建时间，提高稀疏指纹库定位精度，文献[10]和文献[11]采用Kriging 插值方法，减少指纹数据的采集，但未有效处理干扰信号，导致采集的RP缺乏代表性.由于室内信号多径传播和非视距的影响，RSS在一段时间内产生波动.文献[12]将离线指纹库存储多时间段的指纹数据与平均值并用，考虑AP信号的波动性，结合K近邻算法(KNN)获得更准确的位置估计，但K值固定容易出现误匹配.空间中大部分干扰信号被认为是高斯噪声，均值滤波不能有效处理干扰信号，高斯滤波和卡尔曼滤波算法[13-14]被认为能更好地处理含高斯噪声的信号.传统随机森林(RF)模型对具有不同泛化能力的决策树拥有相同的投票权重，影响模型的整体稳定性.文献[15]采用RF算法实现系统的识别功能，但精度较低.为提高RF算法的识别精度，文献[16]对传统RF模型中的决策树根据ROC曲线下方的面积大小(AUC)值计算相似度矩阵，选出AUC最大的决策树组成新的RF模型.文献[17]利用Kappa 系数评价RF决策树分类能力，通过决策树加权策略改进模型，解决数据不平衡带来的少数样本识别率低的问题.此类策略和模型是基于分类任务做的改进，无法直接用于室内定位中的位置识别回归任务.

基于文献[16]和文献[17]优化分类决策树权重的思想，利用袋外数据(OOB)评价决策树回归能力，并为其分配权重，将稀疏采样方法和Kriging 插值方法组合，提出了一种基于指纹库扩充的改进随机森林(FDE-IRF)方法.本文稀疏采样定位范围内的RP，对离线阶段的采样数据进行高斯滤波滤除部分噪声，采用高斯变异函数拟合的Kriging 插值算法自动生成缺失RP的指纹.在在线阶段，对采样数据进行卡尔曼滤波，利用OOB数据计算每棵决策树的定位误差，为预测能力强的决策树分配更高的权重.在实验阶段，进行稀疏采样、扩充指纹库和全采样三种环境下的算法对比实验，证明本文算法的准确性和有效性.

1 指纹库的构建与扩充

1.1 稀疏采样构建指纹库

指纹库的指纹质量影响在线匹配阶段的定位效率和精度，构建稳定可靠的指纹库是指纹定位关键[18-19].

传统指纹库的构建方法是在RP 建立一条指纹信息，极大地节省在线匹配的时间，但只存储一条指纹信息不能充分体现RP的信号波动.由于信号受多径干扰及其他无线电信号的影响，使在线匹配不同时间段的匹配误差增大.

为建立可靠稳定的指纹库，便携式电脑在不同RP对同一AP的Wi-Fi列表进行扫描，观察信号强度的波动，RSS值的变化趋势如图1所示.

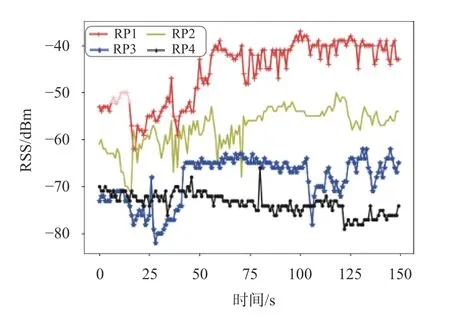
图1 RSS观测值波动情况

由图1可知，Wi-Fi 信号的RSS 值随采样时间变化不停波动，为选择更有代表性的RP指纹信息，本文采用每个RP 多条指纹的指纹库方法，使RP处的指纹更能表示该点的信号波动.假设在区域中有n个AP和s个RP，对RSS信号进行高斯滤波后构建初始阶段指纹库，如表1所示.

图1测得的RSS随时间变化波动比较大，因此，在每个RP存m条指纹数据，使指纹数据更具体真实，充分体现信号的空间特性.

1.2 Kriging 插值扩充指纹库

稀疏采样构建指纹库解决了建库工作量大的问题，但稀疏采样使得网格划分变大，定位精度降低.基于文献[10]和文献[11]的分析，采用Kriging 插值法.Kriging 插值是一种地学统计格网化方法，其试图挖掘隐含在数据中的趋势，对插值点进行无偏估计，同时满足无偏估计条件，插值公式如式(1)所示：

通过变异函数来考量采样点与插值点的空间关系.根据样本数据计算的半方差，选用高斯变异函数拟合模型，如式(4)所示：

式中，半方差γ(·)由式(3)求得，权重系数λi通过求解方程组式(9)求得，代入式(1)即求得待估计点的属性Zˆ(X) ，即AP在待估计点的RSS值.

1.3 位置指纹的定位流程

图2是FDE-IRF室内指纹定位流程，首先稀疏采样多时间段的指纹数据进行高斯滤波预处理完成指纹库构建，然后考虑到Wi-Fi 信号相关性引入Kriging 插值方法完成指纹库扩充，最后在在线匹配时，应用FDE-IRF匹配准则，完成二维位置坐标解算，定位流程如图2所示.

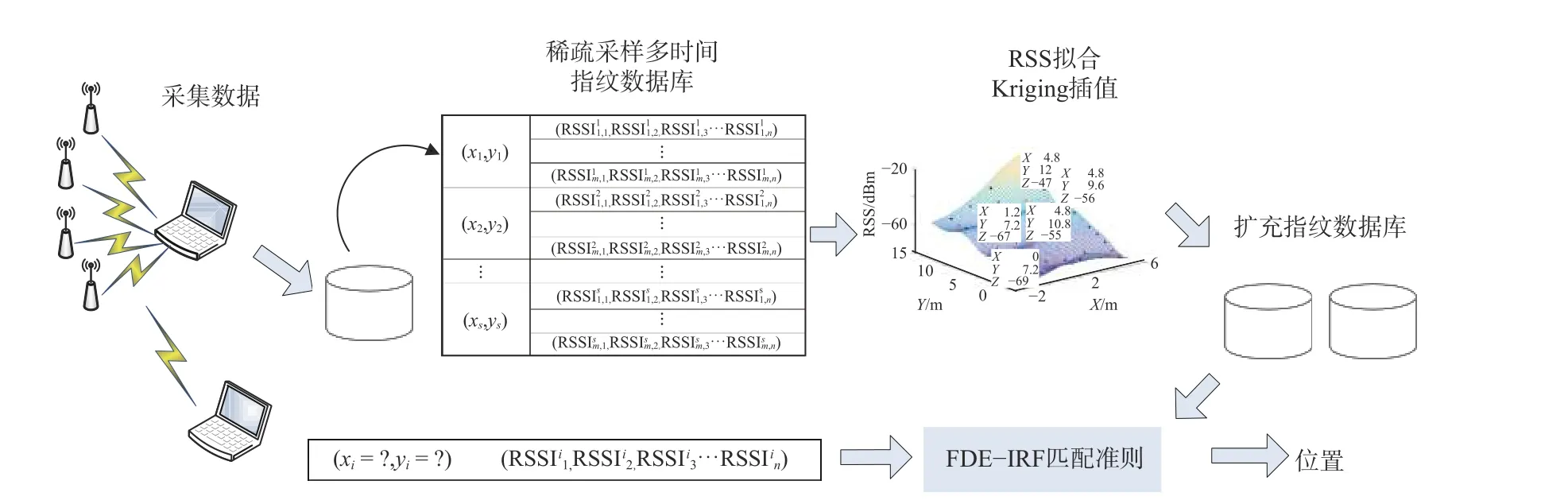
图2 位置指纹定位流程

2 RSS指纹数据拟合与修正方法

2.1 基于高斯滤波的数据拟合

图3是一段时间内RSS观测值的频率分布直方图，呈现高斯分布.为使指纹库更可靠准确，本文对采集的RSS信号进行高斯拟合.

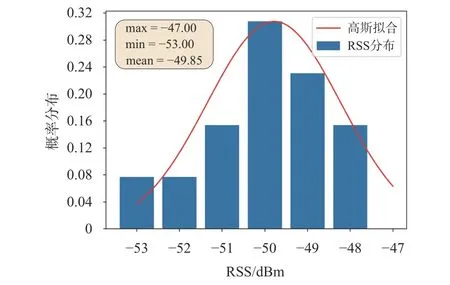
图3 高斯拟合RSS信号

如图3所示，采集到的信号总体满足高斯分布.本文考虑Wi-Fi 信号的分布特性，对离线采集到的数据进行高斯滤波，将RSS范围在[µ−σ,µ+σ]的值保留.文中方法有效过滤跳变大且异常的数据，一定程度上解决了RSS数据稳定性差的问题.本文在构建指纹库时使用高斯滤波，在采集完所有数据后对总体数据进行滤波.

2.2 基于卡尔曼滤波的数据修正

卡尔曼滤波的误差独立存在，滤波自身误差不受测量数据的影响.卡尔曼滤波以最小均方误差为估计，利用观测值对预测值进行修正以获得最佳估计值，通过递推得到优化后的结果.具体操作是将上一时刻的最优估计RSS值作为这一时刻的预测值，再用这一时刻的RSS观测值修正预测值.本文应用卡尔曼滤波完成在线阶段RSS数据的修正.卡尔曼滤波过程分为两个阶段：预测阶段和测量更新阶段.

预测阶段公式如式(14)和式(15)所示：

3 基于FDE-IRF的定位算法设计

3.1 RF定位算法

RF是由大量的决策树构成的，决策树的生成就是递归地构建二叉树的过程.对回归树用平方误差最小化准则，进行特征选择，生成二叉树.

假设X、Y分别为输入和输出变量，并且Y是连续变量，给定训练数据集如式(19)所示：

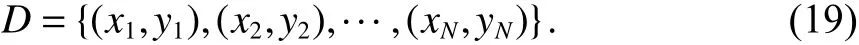
将输入空间划分为M个单元R1,R2,···,RM，并且在每个单元Rm上有一个固定的输出值cm.

回归树模型可表示为式(20)：

用平方误差来表示回归树的预测误差，用平方误差最小准则求解每个单元上的最优输出值.单元Rm上的cm的最优值cˆm是Rm上的所有输入实例xi对应的输出yi的均值，如式(21)所示：

采用启发式的方法，选择第j个变量xj和它的取值s，作为切分变量和切分点，并定义两个区域，如式(22)和式(23)所示：

RF是一种集成学习方法[20]，它通过训练时构建多棵决策树来完成分类、回归等任务，以改进决策树过拟合现象.RF预测结果以每棵决策树输出的均值为最终结果，每棵树的建立依赖于一个独立抽取的样品.森林中的每棵树具有相同的分布，预测误差取决于每棵树的回归能力和相关性.

如图4所示，RF算法的步骤如下：

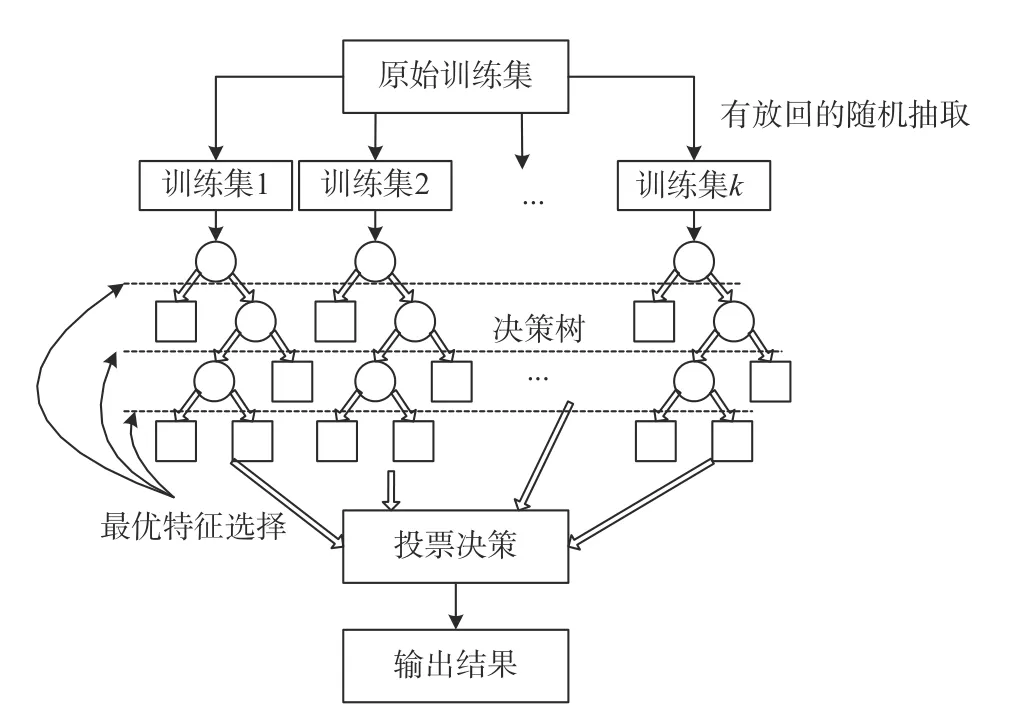
图4 RF算法流程

Step1：样本选择.每棵决策树从原始训练集N中有放回地重复随机抽取k个样本生成新的训练样本集合(k个训练集之间相互独立，元素可重复).

Step2：特征选择.RF选择一个最优的特征划分点来划分决策树.

Step3：构建决策树.在构建决策树时，每个节点的分裂都要按照Step2进行，直到无法分裂为止.

Step4：位置预测.通过Step1～Step3的迭代，构建大量决策树构成森林.将测试样本作为输入，RF模型对测试样本进行回归运算，得到最终的位置坐标.

3.2 IRF 定位算法

在N个样本的原始训练集的随机采样中，被抽取的数据成为训练集，而k次采样都没有被采集到的数据成为OOB数据.利用OOB数据估计决策树的预测能力从而评价RF的性能.OOB数据未被抽样的概率，表示为

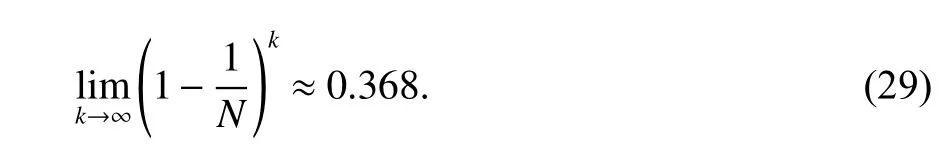
RF算法在构建过程中，以每棵决策树输出的均值为最终结果，但实际每棵决策树的回归能力不同.在构建RF模型过程中，决策树的OOB估计与决策树的构建串行完成，即在完成构建RF模型的同时，所有决策树获得一个相应的OOB估计数值.本文在此基础上优化决策树的投票策略进而优化RF模型.

IRF算法步骤如下：

Step1：同RF算法Step1～Step3.

Step2：决策树权重分配.计算决策树的预测位置与真实位置的欧式距离，将距离平方的倒数作为权重，再将权重归一化作为决策树的权重系数，依次为决策树分配相应的权重wi，如式(30)～(32)所示：

3.3 FDE-IRF定位算法

在室内指纹匹配方法中，全采样构建指纹库费时费力，而传统RF算法由于其固有的决策树平均投票机制使得算法在位置匹配时准确率低，基于此，本文提出一种基于FDE-IRF的室内指纹定位算法.

FDE-IRF室内指纹定位方法的整体算法流程，如图5所示.算法基于2.1节的理论推理，利用高斯滤波剔除异常值，根据1.1节的分析，考虑RSS波动性存储多时间段指纹数据完成指纹库构建.文中算法通过1.2节Kriging 插值的推理，补全在离线阶段稀疏采样的未采样点，得到扩充的指纹库.基于此，本文根据2.2节卡尔曼滤波的理论分析对待测点RSS向量实时修正，基于3.1节RF 模型框架分析，在3.2节引入OOB数据评价手段，根据预测位置与真实位置的欧式距离，为每棵决策树分配权重，改进决策树平均投票策略，优化RF模型，最终解算得到位置坐标.

图5 FDE-IRF定位算法流程

本文所提FDE-IRF室内指纹定位方法的具体实验步骤如下.

离线阶段：

Step1：部署6 个AP下的2.4 m 和1.2 m 网格的实验环境.

Step2：在RP点多时间段采集RSS，分析信号类高斯分布特性，采用高斯滤波剔除异常值.

Step3：分析RSS波动性，存储多时间段RSS向量，构建强代表性指纹库.

Step4：利用Kriging 插值的空间相关性补全2.4 m稀疏采样的未采样点，完成1.2 m 指纹库自动扩充.

在线阶段：

Step1：在待测点采集RSS向量，采用卡尔曼滤波算法实时修正RSS.

Step2：RF模型训练扩充指纹库，生成100棵决策树.

Step3：利用OOB数据的评估手段代入式(30)～(32)计算100棵决策树的权重，将权重代入式(33)得到基于决策树加权的IRF模型.Step4：使用FDE-IRF 算法将实时修正的RSS向量在线匹配，得到解算坐标.

4 实验过程及分析

4.1 数据采集

为验证文中算法的有效性，设计对比实验以评估算法的定位误差.图6是设计的实验环境，实验时偶有人员走动.在地面标定2.4 m×2.4 m 方格，设置参考点21个，测试点12个.实验所用AP 型号为Howay2000Q87，实验的信号采集设备为戴尔便携式计算机，型号为Inspiron 15-5557，电脑网卡型号为Intel(R)Dual Band Wireless-AC 3165，采集程序为Python 脚本.

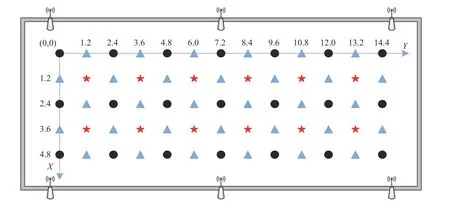
图6 实验环境

图6中圆形点表示原始指纹点，三角形点表示插值指纹点，星形点表示测试点.在每个原始指纹点处采集400条数据，经过高斯滤波后，选取20条质量较好的数据作为该点指纹数据，存入指纹库.将2.4 m稀疏指纹库每隔1.2 m 进行插值，指纹样本约是之前的2.5倍，将插值数据存入指纹库.

4.2 数据预处理

采用的Kriging 插值属于一种最优内插方法，得到的插值面较为光滑，其内插值的可信度依赖于实际指纹采集点的数据密度.选用一组RSS 值进行插值操作，如图7所示.

反距离插值法中点到估计像元的中心越近，则其在平均过程中的影响或权重越大.在相同实验环境下，采用反距离插值法和Kriging 插值法对2.4 m 网格进行1.2 m 插值处理，对12个测试点的AP1的信号强度进行对比，实验结果如表2所示，结果保留整数.

表2 两种插值方法误差对比dBm

通过表2结合图7可知，Kriging 插值法充分考虑空间信号的相关性，在最大误差、最小误差和平均误差评价标准上均优于反距离插值法，插值结果更准确.

为比较滤波算法效果，在同一参考点选取一个AP的RSS数据，对其进行卡尔曼滤波、高斯滤波、均值滤波，如图8所示.

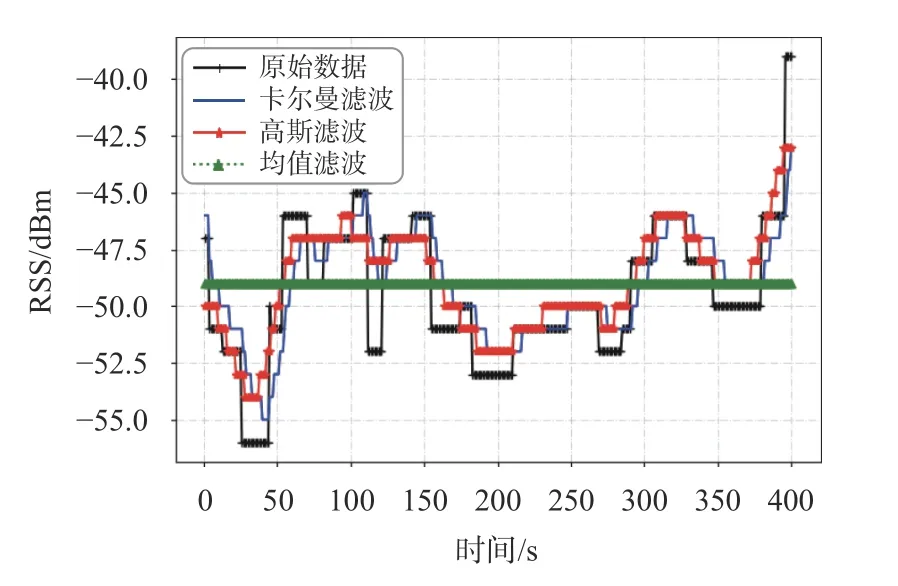
图8 滤波对比示意图

由图8知，卡尔曼滤波、高斯滤波之后的数据波动更为平缓，滤除大部分异常跳变点，减轻由于信号异常对定位产生的影响.卡尔曼滤波是基于前一状态对后一状态的预测，时延较高，高斯滤波的时延较小，在不考虑在线匹配的情况下，高斯滤波的效果更好.

为对比在离线阶段不同滤波方法对指纹数据匹配精度的影响，在相同实验环境下，用RF算法进行在线匹配实验，实验结果如表3所示.

由表3可知，高斯滤波和均值滤波的平均误差较小，但高斯滤波和均值滤波不适用于在线匹配，因为这两种滤波方式要在全部数据上做滤波.若不考虑在线匹配情况，在离线情况下，即建立指纹库时，使用高斯滤波和均值滤波.在线匹配时，选择卡尔曼滤波进行实验数据的处理.

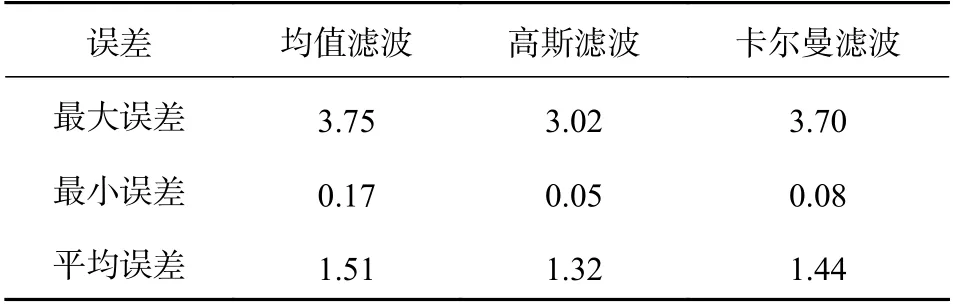
表3 三种滤波方法误差对比m

4.3 结果分析

为验证指纹库自动扩充的准确性和有效性，比较基于2.4 m 稀疏采样+插值的指纹库扩充(FDE)方法和2.4 m 稀疏采样方法在在线匹配时的定位精度，本文按照4.1节部署的实验环境进行实验，RF算法选用100棵决策树.

图9是不同算法指纹库自动扩充前后的平均定位误差对比，用Kriging 插值方法补充未采样的RP，更多的RP参与在线指纹的匹配.指纹库扩充后的加权K近邻(WKNN)、RF、支持向量机(SVM)、IRF算法的平均定位误差均小于扩充前，比扩充前分别提高26.4%、19.0%、7.0%和23.2%.结果表明，指纹库扩充方法在本文实验环境下真实有效，定位精度更高，定位结果更加稳定.

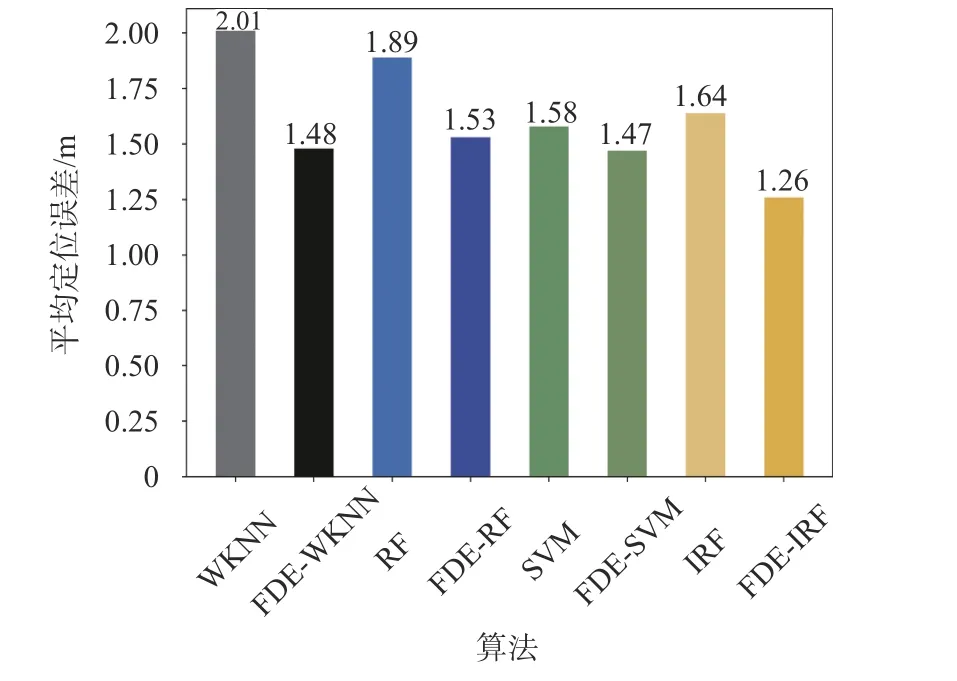
图9 指纹库扩充前后算法定位精度对比

为进一步分析指纹库自动扩充的有效性，本文在4.1节实验环境中，比较了基于2.4 m 稀疏采样+插值的指纹库扩充方法和1.2 m 全采样(AS)方法的定位误差.如图10所示，基于FDE方法的WKNN、RF、SVM、IRF 算法的平均定位误差比AS方法分别提高8.6%、降低3.4%、提高0.7%和降低5.0%，平均误差最多降低0.06 m，基本满足在线室内指纹定位的误差要求.FDE方法在满足定位误差可接受的同时，节省构建指纹库的成本.由图6实验环境的布设RP点数可知，指纹库自动扩充方法采集的RP个数比全采样减少60.4%，采集时间相应地减少相同的比例.

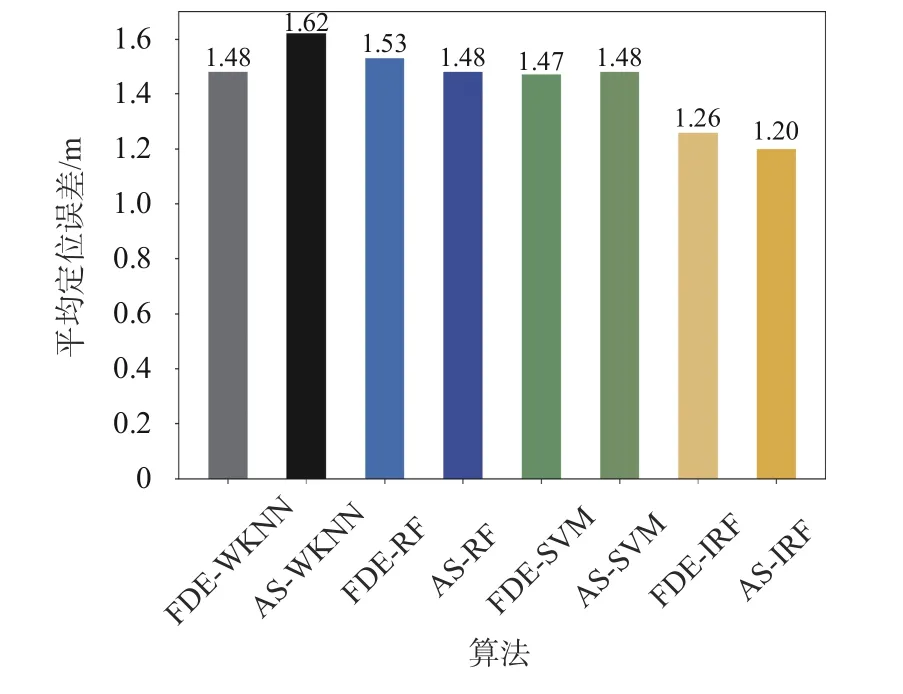
图10 指纹库扩充与全采样定位误差对比

为验证本文所提IRF算法的准确性，基于2.4 m稀疏采样+插值的指纹环境，评估IRF算法与WKNN、RF、SVM 算法在一定误差范围内的定位精度，绘制不同定位方法的误差累积分布概率和误差离散情况，如图11和图12所示.

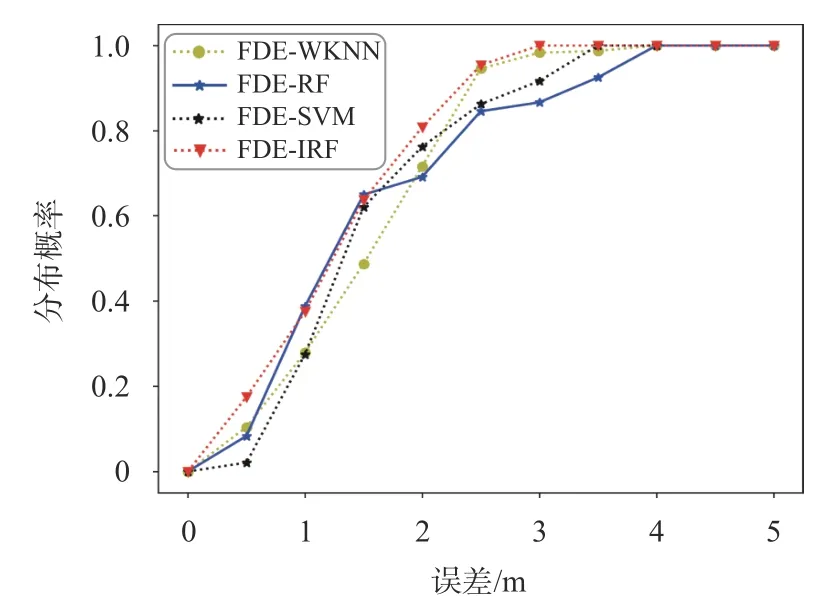
图11 累积分布概率对比

图12 数据离散情况对比

由图11～12可知，在指纹库扩充情况下，同RF、WKNN、SVM 算法相比，FDE-IRF算法在线匹配时所有的测试点定位误差都在3 m 内，定位误差的最大值和最小值都最小，且误差离散程度小，定位效果最好，验证了算法的准确性.由图9可知，本文所提算法其误差较FDE-WKNN、FDE-RF、FDE-SVM算法分别减少14.9%、17.6%和14.3%.使用决策树加权的RF模型的预测精度高于传统RF模型且比随机森林算法稳定，说明通过评估决策树回归能力的大小分配权值的方法合理、可行，引入决策树权重后，提高RF 模型的泛化能力，验证了算法的有效性.

5 结束语

本文提出一种基于FDE-IRF的室内指纹定位方法，通过综合利用稀疏采样、Kriging 插值和IRF算法，有效提高位置指纹算法的定位精度.在离线阶段通过采用自动扩充指纹库的方式，保证定位精度的同时，降低指纹库构建成本；在在线匹配阶段，IRF算法，利用RF随机抽样的OOB数据，评价决策树的回归能力，并根据决策树的回归能力分配相应的权重，优化RF结构，有效地提高了定位精度.