一种基于跳数修正和跳距优化的DV-Hop定位算法

2021-09-14张媛王梅缪相林丁凰

全球定位系统 2021年4期

张媛，王梅，缪相林，丁凰

( 1.西安交通大学城市学院计算机系，西安 710018；2.西安交通大学计算机学院，西安 710049)

0 引言

随着智能信息产业的发展，基于无线传感器网络(WSN)[1]在智慧农业、智能康复医疗和战场防线勘察领域得到了广泛的应用.多数的WSN 应用需要获取节点的位置信息[2]，需通过定位算法估计节点位置，即对节点进行定位.

目前节点定位算法可分为两类：测距和非测距定位.基于接收的信号强度指示(RSSI)[3]、到达时间差(TDOA)[4]和到达角度(AOA)[5]属测距定位算法；质心定位、DV-Hop定位[6]和凸算法属非测距定位算法.相比于测距定位算法，非测距定位算法无需额外的硬件设备测量距离，降低了定位成本.

作为经典的非测距定位算法，DV-Hop 算法被广泛应用于估计节点位置.尽管DV-Hop算法的复杂性低，但其也存在一些不足.如最小跳数估计精度不高，跳距估计误差大.为此，研究人员提出了不同的改进策略.

胡玉兰等[7]提出基于平均跳距优化的DV-Hop改进算法(AHDD).通过对跳数进行优化，提高估计平均跳距的精度；邓浪等[8]对DV-Hop算法的跳数进行优化，并利用最小均方差准则估计平均跳距，提高测距精度；Gao等[9]引入粒子群优化算法，利用粒子群算法修正节点位置，提高定位精度.尽管上述算法减少了定位误差，但仍存在最小二乘法初值敏感以及生物智能算法的复杂度高等问题.

为此，针对DV-Hop算法的定位精度问题，分析了导致定位精度不高的原因，并提出基于跳数修正和跳距优化的DV-Hop定位算法(NHDL). NHDL 算法利用信号强度值对跳数进行修正，并利用锚节点间已知的位置信息对跳距误差进行优化.同时采用易实现的最小最大法估计节点位置.仿真结果表明：提出的NHDL 算法有效地提高了定位精度.

1 DV-Hop定位及误差分析

DV-Hop定位算法主要由三个阶段构成：1)未知节点与锚节点间的最小跳数的估算；2)未知节点与锚节点间的平均跳距的估算；3)未知节点位置的估算.其中，跳数和平均跳距的估计存在较大的误差.

1.1 最小跳数的估算

传统的DV-Hop定位算法不论邻居节点间的实际距离远近，只要接收到邻居节点发送的分组包，就将跳数设置为1.如图1所示，锚节点L1与未知节点A，节点A与节点B的距离不同，但是对于节点A而言，它们离自己的跳数均为1跳.通过这种方式估算跳数，再利用跳数测算距离必然会产生定位误差.

图1 DV-Hop算法误差分析图

1.2 平均跳距的估算

依据DV-Hop 算法估算平均跳距策略，锚节点L1所估算的平均跳距为：( 40+40)/(4+4)=10.未知节点A接收此平均距离信息后，利用跳数与平均跳距的乘积作为离L1的距离： 1 ×10= 10.但是实际上，L1与未知节点A的距离为5.

通过上述分析可知，DV-Hop定位算法在最小跳数和平均跳距的估算阶段存在明显的误差.为此，NHDL 算法将对跳数和跳距进行修正，再通过最小最大法估计未知节点位置.

2 NHDL定位算法

2.1 基于RSSI 的跳数修正

若直接利用分组包传递的次数，估计锚节点间的跳数存在偏差.为此，利用接收的信号强度指示(RSSI)对跳数进行修正.

采用对数衰减模型，通过RSSI 估计距离，如式(1)所示：

图2 信号传输模型

锚节点将修正后的跳数载入分组包中，向下一跳邻居节点广播.接收到分组包后，节点先从分组包中提取跳数值，并检查是否已保留了离发送节点的跳数值. 若已保留，就比较这两个跳数值，并存储两值中的最小值作为这两个节点间的跳数.然后，再将此跳数加1，继续广播分组包.

2.2 基于锚节点位置的平均跳距优化

2.3 定位盲区感知的锚节点选择

文中考虑了节点位置属二维空间.估计二维空间中节点的位置，至少3个锚节点的测距信息.因此，在估计节点位置时，需选择3个锚节点，并建立相应的距离方程.然而，如果所选择的3个锚节点位于同一条直线，即共线，就无法估计节点位置，出现定位盲区[10].

为了避免定位盲区，NHDL 算法先通过行列式法计算3个锚节点所形成的区域面积，再判断区域面积是否为零.若为零，则表示这3个锚节点共线；反之，不共线.具体过程如下：

2.4 基于最小最大法的节点位置估计

首先，未知节点通过修正后的最小跳数以及优化后的跳距，计算离锚节点的距离；然后，利用最小最大法计算自己的位置坐标，即定位.最小最大法的思路如下：未知节点获取离锚节点的距离后，以锚节点位置为圆心以估计的距离为半径形成圆的外接矩形.二维空间的位置，至少需要形成以3 个非共线的锚节点的外接矩形；最后，以3个外接矩形所重叠的区域的中心位置为未知节点位置的估计值.

图3 基于最小最大法的节点位置估计

2.5 定位流程

首先，部署节点.锚节点广播分组包.网络内所有节点通过接收分组包以及RSSI值对最小跳数值进行修正，并存储最小跳数值.

然后，锚节点依据2.2节对平均跳距进行修正，再进行广播分组包，未知节点接收到分组包后，估算离锚节点的距离.当获取3 个以上锚节点后，再从中选择3个非共线的锚节点，并依据最小最大法估计位置，NHDL 定位算法流程如图4所示.

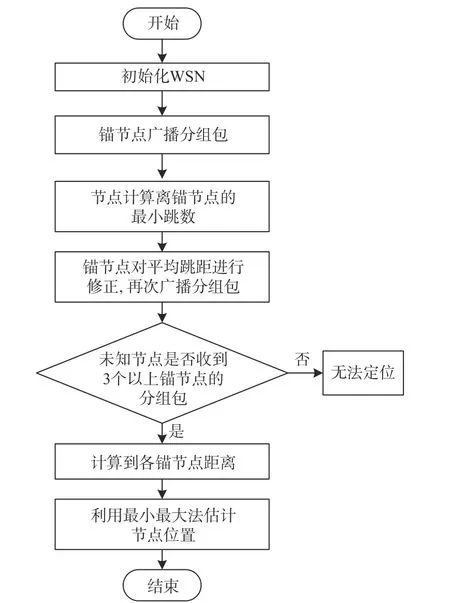
图4 NHDL定位算法流程

3 仿真与分析

3.1 仿真环境

3.2 锚节点数对定位精度的影响

本次实验参数如下：未知节点数n=100；R=20 m；锚节点数从10～40变化.图5给出了DV-Hop算法、AHDD算法和NHDL 算法的平均定位误差随锚节点数的变化情况.

由图5可知，平均定位误差随锚节点数量的增加呈下降趋势.当锚节点数量较少时，增加锚节点数可以有效地降低平均定位误差；但当锚节点数达到一定数量后(大于25)，平均定位误差随锚节点数量增加而变缓慢.这说明并非增加锚节点数就一定能够降低平均定位误差.

图5 锚节点数对平均定位误差的影响

此外，相比于DV-Hop算法和AHDD算法，提出的NHDL 算法具有较低的平均定位误差.这归功于NHDL 算法通过RSSI值对跳数进行了修正，控制了跳数估计的误差.同时，利用锚节点间已知的位置信息，平均跳距进行了优化，最终提高了定位精度.

3.3 未知节点数对定位精度的影响

本次实验参数如下：未知节点数从60～200变化，锚节点个数等于10%的未知节点数，节点通信半径为20 m.DV-Hop 算法、AHDD算法和NHDL 算法的平均定位误差随未知节点数的变化情况，如图6所示.

图6 未知节点数对平均定位误差的影响

由图6可知，节点数的增加有利于定位精度的提升.原因在于：网络内节点数越多，网络的连通性越好，节点能够获取的定位信息越充分.此外，相比于DV-Hop 算法和AHDD算法，NHDL算法在平均定位误差性能方面具有较大的优势.例如，当节点数为200时，NHDL 算法的平均定位误差为0.122 m，而DV-Hop 算法和AHDD算法的平均定位误差分别为0.274 m 和0.237 m.

3.4 通信半径对定位精度的影响

最后，分析通信半径R对定位精度的影响.本次实验参数：未知节点数n=100；锚节点数为10 个；通信半径从15～40 m 变化.

图7给出DV-Hop算法、AHDD算法和NHDL算法的平均定位误差随通信半径R的变化情况.由图7可知，通信半径的增加有利于降低平均定位误差.原因在于通信半径越大，节点通信的范围越大，能够获取的定位信息越多，这有利于提高定位精度.

图7 节点数对平均定位误差率的影响

此外，相比于DV-Hop算法和AHDD算法，NHDL算法降低了平均定位误差.在通信半径较低时，NHDL算法在平均定位误差性能方面的优势更明显.例如，在通信半径为20 m 时，NHDL 算法的平均定位误差为0.183 m，而DV-Hop 算法和AHDD算法的平均定位误差分别为0.520 m 和0.294 m.