GNSS-R 信噪比信号在海面测高技术的研究综述

胡媛，钟李程，陈行杨，顾旺旺，刘卫

( 1.上海海洋大学工程学院上海， 201306；2.上海海事大学商船学院上海， 200135)

0 引言

近年来，全球气候变暖，两极冰川融化导致海平面的上升.随着海平面的上升，海拔低的沿海地带将被淹没，数百万居民流离失所.此外，风暴、极端海浪和飓风等自然灾害频繁发生，因此，监控海平面的变化对于沿海人民的生活有着重大的意义.传统监测海平面的方法是通过岸边验潮仪进行监测，但是传统验潮仪测量的是相对海面高度，其测量结果是绝对海面和地壳垂直方向的形变共同组成的相对海面高度.测量绝对海面高度则需要通过全球卫星导航系统(GNSS)抵消地壳垂直位移的影响，并且传统验潮仪在风浪的作用下，测量仪器可能会出现零点漂移现象[1].

自Hall 等[2]提出全球卫星导航反射信号(GNSS-R)的概念以来，GNSS-R 被广泛应用于遥感方面.如土壤湿度检测[3-8]、降雪深度检测[9-13]、海冰检测[14-17]、海面溢油检测[18-21]，同样GNSS-R 也被运用于监测海平面.1993年，Martin-Neira[22]首次提出被动反射和干涉测量系统，即PARIS(passive reflectometry and interferometry system)的概念，PARIS的主要理论思想是利用从海面反射过来的GPS信号测量海面高度，并且同时测量多个反射点，利用多个卫星信号来达到很高的测量精度.

自PARIS概念提出，许多研究人员在GNSS-R海面测高方面做了大量的研究.目前为止，利用GPS信号测量海面高度可以大致分为两类，相位差分析[23]和信噪比(SNR)分析[24].相位差分析是使用两根天线来确定直射信号和来自海面的反射信号之间的相位差，包括码相位差法和载波相位差法[25]，从而得出两个信号的路径差来确定海面高度.其中直射信号为右圆极化(RHCP)信号，反射信号的极化特性通常情况下从RHCP转变为左圆极化(LHCP)，这种改变由反射面的介电特性和发射机-反射面-接收机的几何结构决定[26].该技术需要运用双天线的接收机，这种接收机结构复杂，成本大并且需要专业人员安装.SNR 分析方法利用单根天线接收直射信号和反射信号所产生的干涉模式技术(IPT)[25]，利用所获得的SNR 与卫星仰角的函数关系来确定海面高度.运用SNR 数据分析只需要单根天线来测量海面高度，并且对风浪条件具有更好的鲁棒性.但是目前该方法的测量精度还不如利用相位差测量方法的精度高，所以许多研究者正在研究运用SNR 数据提高测量精度的算法.本文围绕SNR 数据测量海面高度中运用的算法进行展开，介绍在利用SNR 数据反演海面高度所运用的算法，为以后运用SNR 数据进行海面测高提供一些参考.

1 基于SNR 测高的基本原理

1.1 GNSS-R 测高原理

利用GNSS-R 进行海面测高的基本模型如图1所示，接收机接收来自卫星的直射信号和经海平面反射的反射信号.因为接收机与卫星之间的距离足够远，所以可以认为直射信号和反射信号为平行关系.由图1所示的几何关系，可以得到

图1 GNSS-R 海面测高几何关系图

式中：Δd为直射信号与反射信号的路程差；h为接收机到海面的垂直高度；θ为卫星仰角.

1.2 SNR 信号的数据特点

因为利用SNR 测量海面高度只用了一根天线，所以接收机的信号为反射信号和直射信号发生干涉而形成.根据文献[27]可知，SNR 与接收机之间存在以下关系：

由式(5)中可知，基于SNR 数据反演海面高度，只需要求解出去除趋势项后的SNR 数据的频率.所以寻求合适的算法去除SNR 信号的趋势项和提取去除趋势项后的SNR 信号的频率是利用SNR 信号反演海面高度的关键步骤.去除趋势项和提取频率对反演的海面高度精度起着至关重要的作用.

2 基于SNR 信号的测高方法

2.1 最小二乘法在反演海面高度的应用

2.1.1运用最小二乘法去除趋势项

最小二乘法是一种被广泛应用于消除趋势项的方法[28].如式(2)所示，SNR 数据具有一个二阶多项式的趋势项，SNR 信号的采样数据为{xk}(k=1,2,3,···,n).设趋势项多项式函数

从而得到趋势项多项式的系数，得出趋势项拟合曲线，再用原始的SNR 数据减去得到的趋势项，达到去除趋势项的目的，结果如图2所示.

图2 SNR 信号和拟合的趋势项

2.1.2非线性最小二乘法拟合SNR 信号

通过非线性最小二乘法拟合得到的频率即为去势后信噪比数据的频率，根据式(5)便可以反演出海面高度.

李惟等使用法国图卢兹大学CESBIO实验室的实测数据对上述方法进行验证，同时与LSP方法进行对比.具体结果如表1所示.

表1 LSP 法和拟合法反演结果m

2.2 LSP在反演海面高度的应用

SNR 信号在时间上是均匀采样的，但是实际接收机接收的SNR 信号因变量是卫星仰角的正弦值，这导致SNR 信号是非均匀分布的，并且接收信号时存在噪声干扰.在运用傅里叶变换时，这些噪声和不均匀分布会对频谱分析产生影响，造成频谱图与SNR 信号实际结果偏差很大.Larson K M 等[24]提出运用Lomb标准化周期图(LSP)方法对SNR 进行分析，获取该信号的频率.

LSP是由Lomb[31]于1976年提出，并在1986年由Scargle[32]进行修改完善，LSP有sin 和cos两组基，并且在时域方面做了归一化的处理.因此，LSP方法能够有效地提取时序中的弱周期信号，并且能够减少非均匀采样产生的虚假信号所带来的影响.

运用LSP方法获取去除趋势项后SNR 的频率后，根据式(5)反演得出海面高度，如图3所示.

图3 LSP分析结果

2.3 小波算法在海面测高中的应用

小波分析与傅里叶变换和LSP 相比，傅里叶变换和LSP是全局的变换，得到的是一维的频域信息，而小波分析是一个时间和频率的局域变换.因此小波分析能够有效地从信号中提取信息，解决傅里叶变换所不能解决的诸多问题[33].Wang 等[34]使用小波分析对SNR 信号进行去噪处理，并使用不同长度的SNR信号进行验证.结果表明：在较短的SNR 信号中，使用小波分析去噪精度与未使用小波去噪相比提升了20%.Chen 等[35]和苏晓容等[36]提出了运用小波算法去除噪声.王杰等[37]提出了运用小波算法提取去除趋势后的SNR 信号的频率来反演海面高度的方法.

因为在实际采样中，SNR 信号是一个离散非连续的信号，并且使用连续小波变换计算量太大，所以在处理实际的SNR 信号时使用的是离散小波变换(DWT).将伸缩系数a和平移因子b进行离散化处理，具体如下：

2.3.1小波去噪原理

1989年，Mallat[38]提出了一种快速DWT 算法，使用小波滤波器分解和重构信号，具体如下：

式中：t是离散的时间序列号；f(t)表示原始信号；j是分解信号的层数；H和G分别是小波的低频和高频滤波器.

根据上述描述，将原始信号通过高通和低通滤波器，将信号分解成低频部分和高频部分，然后再将分解的低频部分再分解成低频部分和高频部分，从而实现信号的多层分解.小波分解的原理图如图4所示.

将分解出来的高频系数进行相应小波系数处理去除噪声部分，然后再对分解的信号进行重构处理，这样就可以得到去除噪声后的SNR 信号.

2.3.2小波算法提取频率

运用小波变换提取去趋势后SNR 信号频率，是将趋势后的SNR 信号与经过拉伸或压缩后的小波进行比较，通过在不同尺度m>0和不同位置n比较原信号与处理后的小波，可以得到一个关于两个变量的函数.对于去除趋势后的SNR 信号，小波变换可以表示为

针对上述方法，王杰使用美国SC02站数据进行验证.运用小波分析反演海面高度，标准差略高于LSP法，但是其可以极大地提高反演海面高度的时间分辨率.具体结果如表2所示.

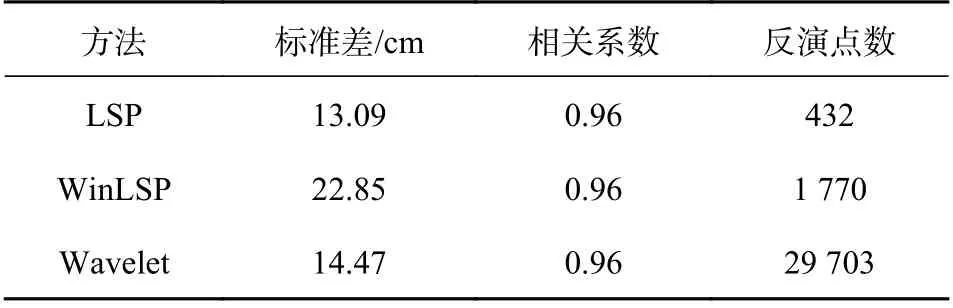
表2 LSP法、加窗LSP法和小波法反演结果

2.4 B样条函数和卡尔曼滤波在海面测高的应用

2.4.1 B样条函数在海面测高的应用

2016年Strandberg[29]提出使用B样条函数对海面高度进行建模，该方法考虑到监测的海平面是连续变化的，可以将海面高度变化假设为一个平滑函数.将海面高度变化作为分段线性模型进行建模可能是最为简单的方法，但是分段线性模型在计算一阶导数时会导致节点处的不连续，不能对海面高度提供足够的可变性用来考虑次日和长期的海平面变化.B样条函数的基本函数定义为

2.4.2卡尔曼滤波在海面测高的应用

之前通过SNR 数据反演海面高度的方法是提取接收机接收的一段时间内的SNR 信号数据，提取出含有高度信息的频率，然后反演海面高度，该方法只能得出该时间内的平均海面高度，并不能提供实时的海面高度数据.卡尔曼滤波[39]是当前应用最广的一种动态数据处理方法，但原始的卡尔曼滤波是建立在线性系统的基础上的，对非线性系统效果并不理想[40].在2000年，Merwe等[41]提出无损卡尔曼滤波处理(UKF)更新步骤中的非线性.在2019年，Strandberg等[42]提出了运用无损卡尔曼滤波实现实时监测海面高度.该方法采用了一个预测方程，可以预测状态向量和协方差矩阵的变换，即：

采用二次B样条函数来描述海面高度随时间的变化，我们需要估计一组缩放系数αi就可以在任何时间预测海面高度，即

B样条函数定义如式(19)～(20)所示，如式(34)所示，想要知道某个时间点所对应的高度，只需要知道该时间点附件的4个节点.随着卡尔曼滤波随着时间的推移，4个节点B样条系数和相应的协方差会不断的更新，直到引入tj+1处的新节点.然后将最后一个节点从状态向量中删除，将前3个节点往后移，为新的节点释放空间.这样卡尔曼滤波便可以连续且实时的估计海面的高度.

针对上述方法，Strandberg 使用GTGU 站数据进行验证.卡尔曼滤波法误差为1.98 cm，并且随着时间的推移，误差缩小为1.48 cm.同样的实验数据，使用LSP方法的误差为8.84 cm.

3 结束语

GNSS-R 遥感作为一个新兴的领域，在各个领域中有着广泛的应用.本文主要介绍了GNSS-R 在海面测高的研究进展，着重介绍了使用SNR 数据反演海面高度的研究进展.主要利用了最小二乘法，LSP法、小波算法、卡尔曼滤波、B样条函数等算法在处理SNR 数据进行海面测高的应用.目前，基于SNR数据测量的方法比之前的基于相位差的方法所需要的设备更为简单且安装更加简便，更具有应用潜力.当前，人工神经网络发展迅速，在诸多领域得到广泛的应用.神经网络特别适合变量之间关系复杂、耦合度高难以直接数学描述的应用场景，在GNSS-R 遥感技术的其他领域，如海冰遥感、土壤湿度检测、海面溢油、海面风场反演等领域都有成功应用.但目前为止，神经网络并未在海面测高方面有所应用，对于提取特征频率的方面还可以利用神经网络的优势来提高反演海面高度的精度.