自然灾害社会易损性模糊综合评判

彭章宏

摘 要：选取表征自然灾害易损性的灾害指标和社会经济指标，应用多级模糊评判方法，计算出茂名市下辖的2区3市的自然灾害易损度。结果表明：信宜市的区域易损度归属于极易损区;高州市的区域易损度归属于高易损区;电白區、茂南区的区域易损度归属于中易损区;化州市的区域易损度归属于低易损区。区域易损度空间分布差异的原因，还需要结合各区域的自然、经济等因素加以系统分析。

关键词：自然灾害;社会易损性;模糊综合评判;茂名

中图分类号：X43文献标识码：A文章编号：1003-5168（2021）12-0141-03

Fuzzy Comprehensive Evaluation of Social Vulnerability to Natural Disasters

—Based on Maoming Region

PENG Zhanghong

（School of Tourism， Guangdong Preschool Normal College in Maoming，Maoming Guangdong 525200）

Abstract： Natural disaster vulnerability index and social economic index are selected and multilevel fuzzy evaluation method is applied to calculate natural disaster vulnerability degree of 2 districts and 3 cities in Maoming area. The results show that the regional vulnerability of Xinyi belongs to the extremely vulnerable region. Gaozhou belongs to the high vulnerability area. Maonan belongs to the middle vulnerability area. Huazhou belongs to the low vulnerability area. The reasons for the differences in the spatial distribution of regional vulnerability should be systematically analyzed in combination with the natural and economic factors of each region.

Keywords： natural disasters;social vulnerability;fuzzy comprehensive evaluation;Maoming region

随着人口的激增和经济的快速发展，人类生存的地理环境正在逐步退化，各种自然灾害频繁发生，人类所遭受的社会经济损失越来越严重。2004年的印度洋海啸，2008年的缅甸热带风暴“纳吉尔斯”、中国汶川特大地震，2011年的菲律宾热带风暴“天鹰”、美国飓风“艾琳”、日本9.0级特大地震、加勒比岛国海地大地震等，均造成了重大人员伤亡和严重的经济损失。据统计，进入21世纪的第一个10年，共发生3 852起国家范围内的自然灾害事件，人员伤亡达到72万人，经济损失高达9 600亿美元。为此，美洲国家组织秘书处的S.O.Bender提出了“区域易损性的估计问题”。区域易损性即一个地区遭遇灾害时容易受到损害的程度，它是政府部门在制定社会经济发展规划和进行宏观调控时必须考虑的一个制约因子。

茂名地处低纬，受地形、海陆和人类活动等影响，台风、洪涝、干旱、泥石流等自然灾害频发，严重制约其经济社会的可持续发展。迄今为止，国内外学者对茂名市开展自然灾害的社会易损性评价的研究非常罕见。本文拟以茂名市为研究对象，提出用区域易损度来估计区域易损性。由于区域易损度涉及的因素较多，而它的界线又是不分明的，因此，拟根据模糊综合评判的原理和方法来确定区域易损度，从而为进一步研究茂名自然灾害提供相关依据，为政府决策提供科学的基础[1-3]。

1 指标体系

自然灾害是致灾因子和人类社会相互作用的结果。一个地区遭受自然灾害损害的程度与很多因素有关，不仅取决于当地的灾害发生频率及灾害强度等致灾因子，而且还与当地的基础设施建设水平和抗灾能力有关，即与人类社会本身有关，人类社会因素一般用社会经济状况来衡量。以洪水灾害为例，洪水如果发生在荒无人烟的地方，即没有人类社会因素的存在，就不是洪水灾害，而仅仅是洪水这样的自然变异;而若发生在有人类活动的地方，会对人类社会和自然资源造成极大损失，形成洪水灾害。但是，人类社会经济状况是很复杂的，不同的国家，甚至同一国家的不同地区，由于经济发展水平的差异，灾害发生和造成的影响是不同的。如果把这些因素都作为评价指标，将会得到一个庞大复杂的指标体系。为此，遵循简练、独立、可操作性原则，选用最能反映区域易损性的9个主要指标（[xi]），并分成两个指标子系统，即灾害子系统[X1]和社会经济子系统[X2]，那么指标系统[X=X1，X2]。各子系统的指标如下：

灾害子系统为[X1][=x1，x2，x3。].其中，[x1]为全年暴雨平均次数;[x2]为寒露风概率;[x3]为年最长霜冻日天数（d）。

社会经济子系统为[X2][=x4，x5，…，x9。]其中，[x4]为60岁以上老人数（个）;[x5]为有科技活动单位数（个）;[x6]为银行存款总额（亿元）;[x7]为职工平均工资（元）;[x8]为人均GDP（元）;[x9]为城市建成区面积（km2）。

在灾害子系统中，全年暴雨平均次数、寒露风概率、年最长霜冻日天数分别从降雨、强冷风、低温等灾害方面反映了一个地区的易损程度;在社会经济子系统中，60岁以上老人数、有科技活动单位数、银行存款总额、人均收入、城市建成区面积则从人口身体素质、抗灾能力和城市建设强度等方面反映了一个地区的易损程度。在这些指标中，有科技活动单位数、银行存款总额、职工平均工资、人均GDP与区域易损度成反比，其余指标则与区域易损度成正比。因此，一个地区的灾害强度越大，社会经济越不发展，就越容易被损坏，易损度就越高;反之，一个地区的灾害强度越小，社会经济越发展，就越不容易被损坏，易损度就越低[4-6]。

2 原理和方法

由于影响一个地区自然灾害社会易损性的因素较多，而且涉及模糊不确定性因素，结合上述指标系统分类，采用二级模糊综合评判。首先对各指标进行低层次、小系统的一级综合评判，然后对评判结果进行高层次、大系统的二级综合评判。具体步骤如下。

2.1 划分指标集[X]、评判集[U]，确定各因子评价标准

首先将一个地区的自然灾害社会易损性指标[X]划分为灾害子系统[X1]和社会经济子系统[X2]，即[X=X1，X2]。为了减小数值较大的指标对评价结果产生过大的影响，需要对原始数据进行标准化处理，因[x1、x2、x3、x4、x9]与易损程度成正比，其处理方式为：[x'=xi/ximax];[x5、x6、x7、x8]与易损程度成反比，则处理方式为：[x'=1-xi/ximax]。经这样处理后，9个因子的作用性质就一致了，式中[xi]表示各因子数列中的每一项，[ximax]表示该因子数列中的最大值。

然后将一个地区的自然灾害易损度划分为4个等级，即评判集[U][={1、2、3、4}]={（极易损）、（高易损）、（中易损）、（低易损）}。

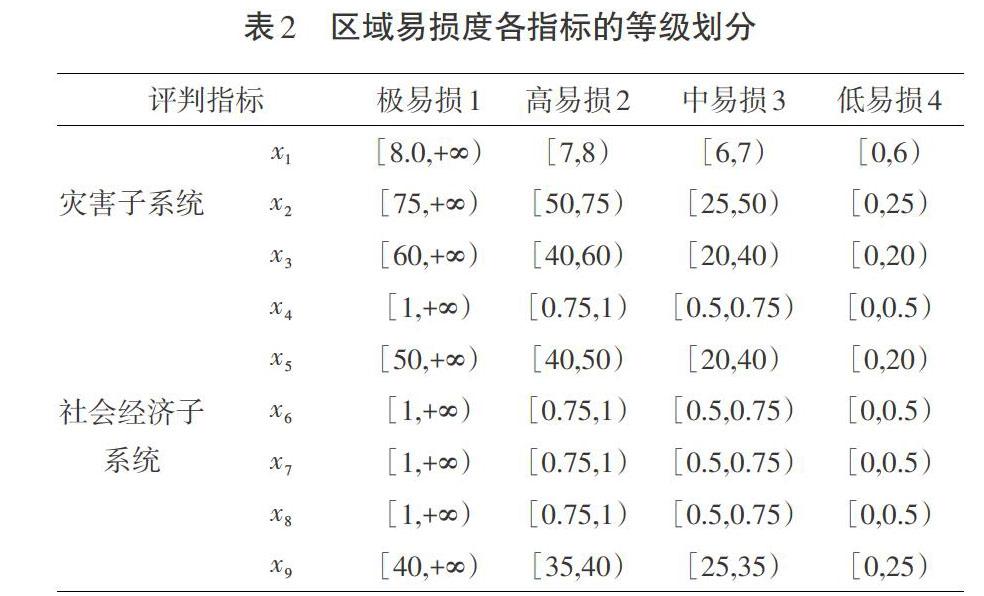
接着建立各因子的评价标准。

2.2 计算隶属度，给出单因子评价矩阵R

隶属度通过隶属函数求得。隶属函数种类较多，结合本文实例，选取均匀分布作为隶属函数，其数学模型为：

[u1xi=ri1=1，xi≥xi10，xi

[ujxi=rij=1，xj，j+1≤xi

[umxi=rim=1，xi

式中：[xij]表示第[i]种指标第[j] 等级的分级标准;[xi]表示某一地区第[i]种指标的数据;[ujxi]表示某[i]指标对第[j]级的隶属度。

2.3 建立权重模糊矩阵B

利用专家打分法，对所有指标中任意两个指标按重要性进行两两比较，给出平均比值[Bij]，得到权重模糊矩阵。

B[=b11b12…b1nb21b22…b2n???bm1bm2…bmn]                  （4）

对矩阵B的每一行元素先连乘，再求[n]次方根，得到列向量[β=β1，β2，…，βnT]，即[βi=j=1nbij1n][i=1，2，…n。]再作归一化处理，即令[ai=βi/i=1nβi]，从而得到权重集[A=（ai，a2，…，an）T]，显然[i=1nai=1]。

经过以上处理，可得到灾害子系统权重集[A1=0.50，0.20，0.30]，社会经济子系统权重集[A2=0.21，0.25，0.13，0.11，0.09，0.19]，指标系统权重集[A=0.55，0.45。]

2.4 一级、二级综合评判

根据单因子评价矩阵R[1]、R[2]，通过模糊合成运算（矩阵乘法），得到[B1=A1×]R1，B[2=A2×R2]。B[1]、B[2]为各指标子系统的一级模糊综合评判集。指标系统的模糊关系矩阵即为B[=B1，B2T]，将指标系统权重集[A]与模糊关系矩阵B进行第二次模糊合成运算，得到最终评判集[F]。根据上述分析，[F]应是只包含4个元素的行向量，根据最大隶属原则，确定4个元素中的最大值对应的评判等级，即可得最后评判结果[7-11]。

3 应用实例

现以茂名市的2区3市（县级市）为例来说明区域自然灾害社会易损度的模糊综合评判问题。表1是根据《茂名统计年鉴》2005—2015年10年来的相关数据平均化后的易损性指标原始数据;表2是根据相关文献及广东省专家意见给出的标准化后的等级标准。

同时，根据专家咨询意见和式（1），得到下列各指标的权数集：灾害子系统权数集[A1]=（0.21，0.24，0.22，0.17，0.16）;社会经济子系统权数集[A2]=（0.28，0.26，0.23，0.23）;指标系统权数集[A]=（0.65，0.35）。

以高州市为例，利用其灾害子系统的基础数据（见表1），并根据式（2）至（4）和表2的分级标准，得到灾害子系统的评判矩阵R[1]，同理可得社会经济子系统的评判矩阵R[2]。在此基础上，进行一级综合评判，得到高州市灾害子系统的综合评判结果[B1]，同理，可求出高州市社会经济子系统的一级评判[B2]，然后进行二级综合评判[B=A×R=（0，0.26，0.74，0）]。

根据最大隶属原则，由于在[B]=（0，0.26，0.74，0）中，最大值（0.74）对应于第二等级，因此，高州市的区域易损度归属于高易损区。

同理，得到信宜市的区域易损度归属于极易损区;电白区、茂南区的区域易损度归属于中易损区;化州市的区域易损度归属于低易损区。

4 结论

从上述分析可以看出，信宜市的区域易损度归属于极易损区;高州市的区域易损度归属于高易损区;电白区、茂南区的区域易损度归属于中易损区;化州市的区域易损度归属于低易损区。由于区域易损度所涉及的因素较多，而它的界线又是不分明的，因而利用模糊综合评判来对其进行研究是一条有效的途径，并且计算方法简单易行。这种方法不仅可以用来评价县（市）、乡（镇）、中小城市等小范围的区域易损性，也可用来评价省、市、自治区、大城市等大范围的区域易损性。通过模糊综合评判，可以全方位地了解各地区的易损程度，这不仅能为各级领导进行科学管理和宏观决策提供重要的信息，而且也能为理论工作者制定政策提供可靠的依据，具有重要的实际意义。这种方法的不足之处是不能解释区域易损度存在空间差异的原因，这也是定量化方法普遍存在的问题，要想系统地研究区域易損度的空间差异，还应该从各区域本身的自然和社会经济情况去考虑，把定量方法和定性方法进行有机结合，这是下一步研究需要努力的方向。

参考文献：

[1]冯德益，楼世博，林命周，等.模糊数学方法与应用[M].北京：地震出版社，1983：74-76.

[2]张撼.应用模糊数学[M].重庆：重庆大学出版社，1985：54-58.

[3]周拒乾，唐川.模糊评判模型在边坡稳定性评价中的应用[J].自然灾害学报，1995（3）：73-82.

[4]刘丽，王士革.云南昭通滑坡、泥石流危险度模糊综合评判[J].自然灾害学报，1995（4）：261-266.

[5]项源金、张向丽.铁路客票发售和预订系统总体方案评价[J].铁道学报，1996（2）：85-92.

[6]程启月，邱菀华.作战指挥效能评估的模糊优化决策分析[J].系统工程理论与实践，2002（9）：112-140.

[7]辛明军，李伟华，何华灿.分布式问题求解方案的模糊综合评价模型及其算法实现[J].计算机工程与应用，2001（15）：40-42.

[8]周穗华，张小兵.模糊综合评估模型的改进[J].武汉理工大学学报（信息与管理工程版），2003（5）：4-7.

[9]全林，赵俊和.效用评估的模糊效用方法[J].上海交通大学学报，1997（4）：121-123.

[10]陈守煜，赵瑛琪.模糊优选（优化）理论与模型[J].应用数学，1993（1）：1-6.

[11]陈耀辉，孙春燕.模糊综合评判法中的最大隶属原则有效度[J].重庆师范学院学报（自科学版），2001（1）：45-47.