敏感型和耐药型HIV毒株感染模型的全局动力学

陈 伟， 滕志东

（新疆大学 数学与系统科学学院，新疆 乌鲁木齐830046）

众所周知，HIV病毒侵入人体后，人体的免疫功能遭到破坏，最终导致人体死亡，1982年被正式命名为艾滋病.艾滋病毒有3种传播方式：血液传播、母婴传播和性接触传播.目前，许多具有特异性免疫反应的病毒动力学研究日益受到重视，这些研究对预防和控制艾滋病有一定的指导作用［1-6］.

在治疗HIV感染患者方面，有4类抗逆转录病毒（ARV）药物：

1）核苷/核苷酸逆转录酶抑制剂（NRTIs），

2）非核苷逆转录酶抑制剂（NNRTIs），

3）蛋白酶抑制剂（PIs），

4）进入/融合抑制剂（EIs）［7］.每种药物针对病毒生命周期的不同阶段.HIV耐药的出现最早是由一些核苷抑制剂记录的，这些抑制剂通过其作为DNA链终止剂的活性抑制病毒复制［8］.在临床中，艾滋病毒耐药性可由耐药突变体向易感个体传播或通过在治疗期间产生的突变而产生.Rong等［9］提供了一个理论框架，用于探索在使用其他HCV蛋白酶抑制剂或聚合酶抑制剂治疗期间，预先存在的突变变体的患病率和耐药性的演变.

为了研究HIV感染患者在治疗过程中产生耐药性的机制，Rong等［7］提出了如下包括敏感型和耐药型毒株的动力学模型

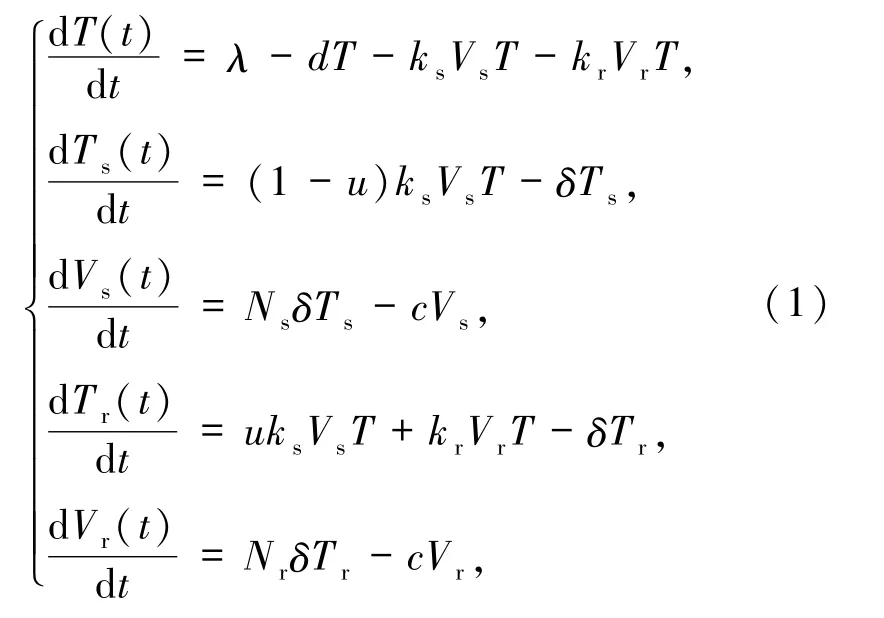
其中，T（t）为未感染细胞在时间t的浓度，Ts（t）为敏感毒株感染细胞在时间t的浓度，Tr（t）为耐药毒株感染细胞在时间t的浓度，Vs（t）为敏感毒株在时间t的浓度，Vr（t）为耐药毒株在时间t的浓度，λ为未感染细胞的补充率，d为未感染细胞的病死率，ks为敏感毒株感染细胞的感染率，kr为耐药毒株感染细胞的感染率，δ为感染细胞的病死率，Ns为敏感毒株的释放率，Nr为耐药毒株的释放率，c为游离病毒的清除率.

在模型（1）中，参数u（0＜u＜1）是病毒RNA逆转录成原病毒DNA（简称SR转化）过程中，敏感型毒株发生突变并且产生耐药性的转化率.需要注意的是，在开始治疗之前，宿主体内就存在大量的敏感毒株，因此从耐药型向敏感型毒株的后向突变就可被忽略［10-11］.为了准确地计算出模型的平衡点，以及确定模型平衡点的稳定性，生物动力学的入侵阈值，即传染病中基本再生数的概念起着决定性的作用［12］.

文献［7］仅研究了模型（1）中无病平衡点，具有耐药型毒株感染的边界平衡点以及共存平衡点的存在性和局部稳定性［7］（命题1和命题2），全局动力学包括平衡点的全局渐近稳定性和HIV感染模型的一致持续性都没有考虑.因此，在本文中，将对这些问题进行深入研究.对无病平衡点、具有耐药型毒株平衡点、共存平衡点的局部及全局稳定性和HIV感染模型的一致持续性建立了一系列的阈值准则.

1 基本性质

对任意整数n＞0，定义

模型（1）的初始条件可表示为

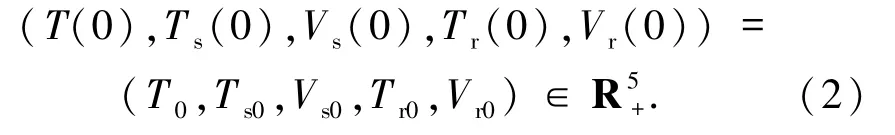
关于模型（1）解的正性和有界性，有定理1.

定理1对任何初始值

模型（1）具有初始条件（2）的解

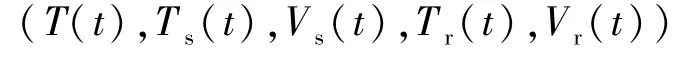
在t∈［0，∞）上有定义，非负且最终有界.

证明首先，证明解的非负性.显然，只需要证明对满足任意正初始值（T0，Ts0，Vs0，Tr0，Vr0）的解（T（t），Ts（t），Vs（t），Tr（t），Vr（t））也是正的.定义m（t）=min｛T（t），Ts（t），Vs（t），Tr（t），Vr（t）｝，则有m（0）＞0.用反证法.假设存在一个t*＞0使得m（t*）=0，并且对所有的t∈［0，t*）有m（t）＞0，则有以下5种情形：

1）m（t*）=T（t*），2）m（t*）=Ts（t*），

3）m（t*）=Vs（t*），

4）m（t*）=Tr（t*），

5）m（t*）=Vr（t*）.

对于情形1），由于当t∈［0，t*）时有m（t）＞0，则从模型（1）的第一个方程有

因此，可以得到0=Ts（t*）≥Ts（0）e-δt*＞0，矛盾.与上述论证类似，可以得到情形3）、4）和5）都是矛盾的，这表明m（t）总是正的.因此，解（T（t），Ts（t），Vs（t），Tr（t），Vr（t））是非负的.

下面证明解的最终有界性.定义Lyapunov函数

这说明解（T（t），Ts（t），Vs（t），Tr（t），Vr（t））也是最终有界的.定理得证.

根据在文献［12］中提出的传染病基本再生数的概念，定义如下敏感型毒株感染基本再生数Rs和耐药型毒株感染基本再生数Rr为：

其中，1/c表示毒株i（i=r，s）的平均生命周期；λ/d表示毒株i在感染过程开始时，少量病毒感染易感细胞的感染细胞数量（接近于无感染稳态）；ki Ni代表一个i型毒株在其平均存活时间内产生的病毒颗粒数量.将这些量全部乘积起来就可以得到一个i型毒株感染细胞产生新的感染细胞的数量，也就是Ri.

下面讨论模型（1）平衡点的存在性.平衡点可以由下列方程组得到

通过求解方程组（4），很容易得到定理2.

2 全局稳定性

令E=（T，Ts，Vs，Tr，Vr）是模型（1）的任意平衡点，则在平衡点E处的Jacobi矩阵如下

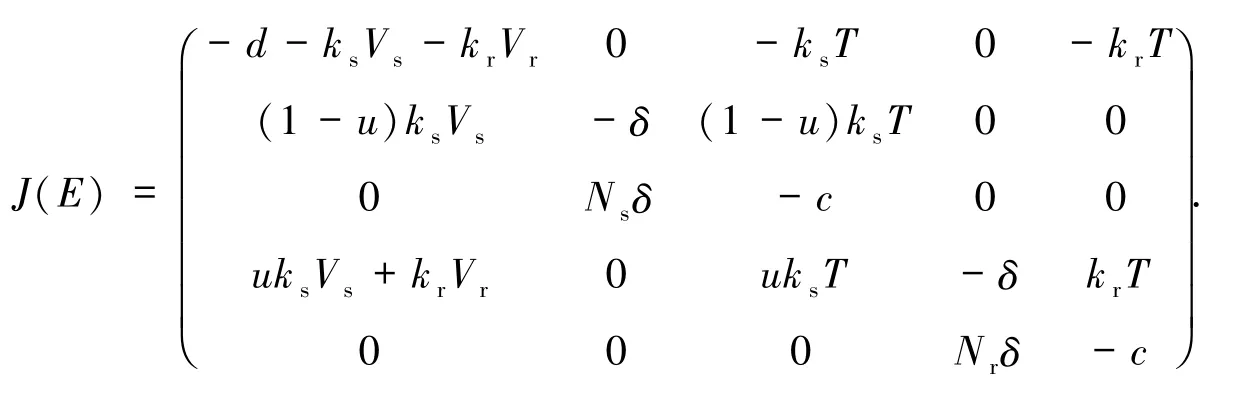
（5）式的一个根为X1=-d.当（1-u）Rs＜1且Rr＜1时，方程

3 一致持续性

定理6 如果（1-u）Rs＞max｛1，Rr｝，则模型（1）是一致持续的.也就是说，存在一个正常数δ，使得对模型（1）的任意正解（T（t），Ts（t），Vs（t），Tr（t），Vr（t）），都有

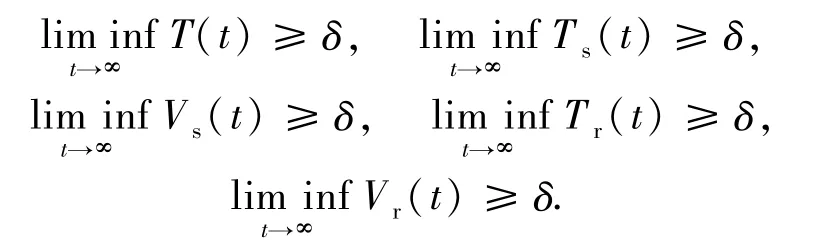
证明对任意

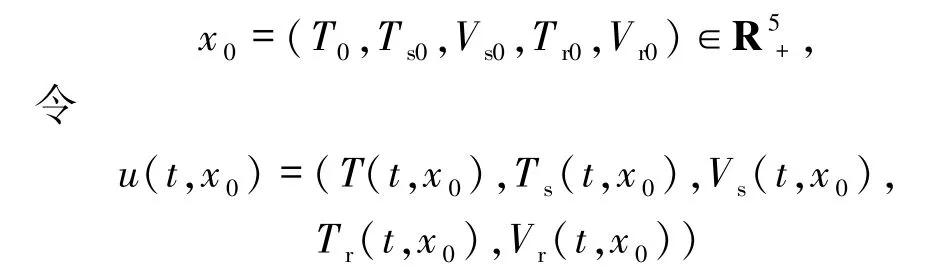
是模型（1）具有初始条件u（0，x0）=x0的解.从定理1的证明可以得到

4 数值模拟

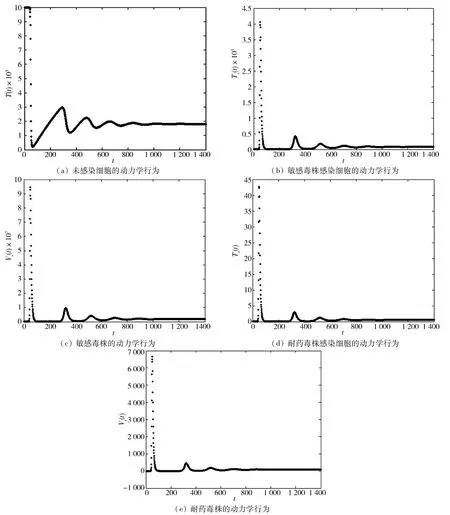
图1 HIV感染模型的动力学行为Fig.1 Dynamical behaviors of HIV infection model

表1 模型（1）的初始值Tab.1 The initial values of model（1）

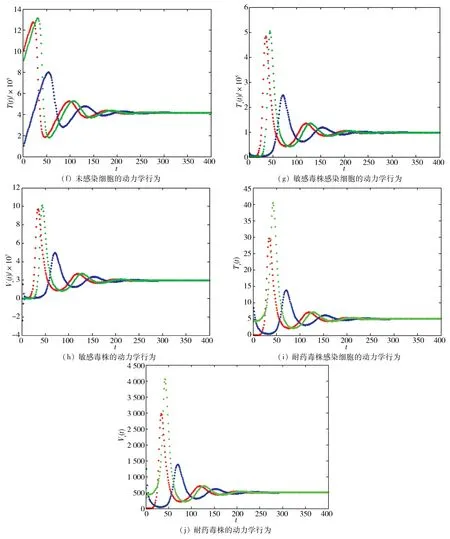
图2 HIV感染模型的动力学行为Fig.2 Dynamical behaviors of HIV infection model

5 结论

本文主要研究了敏感型和耐药型2种毒株的HIV感染模型的全局动力学.敏感毒株在逆转录过程中会发生突变并产生耐药性.主要结果在定理1～定理6中给出.具体地说，在定理1中得到解的正性和有界性，在定理2中计算出耐药型毒株感染平衡点和共存平衡点，定理3～定理5中分别得到每个平衡点的局部和全局渐近稳定的充要阈值条件，在定理6中建立HIV感染模型的一致持续性.

同样也有很多问题值得更深地去研究.首先，注1～注3考虑了一个有趣的开问题就是能否在对应的条件下建立平衡点的全局渐近稳定性.其次，研究更加复杂的模型，比如具有饱和发生率的2种毒株感染模型［15-16］.此外，具有空间扩散的多毒株感染模型平衡点全局稳定问题和具有年龄结构感染模型的动力学行为［17-18］等问题仍然值得去研究.