铁路客运站调机运用与列车进路排列协同优化方法
2021-09-12霍亮
霍亮
(中铁第四勘察设计院集团有限公司,湖北 武汉430000)
既有线铁路客站行车工作内容主要包括列车接发作业进路排列、咽喉与到发线利用和调机运用三个问题,三者之间既相互联系又相互制约。繁忙铁路客运站在组织接发列车时,如何在保证行车设备占用相互协调的情况下,科学调度各项作业的设备使用,最小化设备总的占用时间和最大化设备运用效率,是铁路客运站行车技术作业效率提升的关键所在。目前针对铁路车站的列车接发作业进路排列、咽喉与到发线利用等问题,已经有较为广泛的研究。史峰等[1−2]分别提出了车站咽喉进路与车站进路排列优化模型与算法;AL‐HOSSEIN 等[3−4]研究了高速铁路车站进路排列问题;马驷等[5]构建了高铁车站列车进路分配方案的优化调整方法;SELS 等[6]致力于实现车站站台运用与列车进路自动排列;MIAO 等[7]以提高方案稳定性为目标优化车站站台安排问题;郎越等[8−10]提出高速铁路车站列车进路分配与作业计划链式优化方法。总体而言,既有文献分别对上述3个问题的优化方法进行了独立的分析和研究,这些单一优化方法尽管对实践工作具有一定的指导作用,但由于忽视了三者之间的整体性和关联性,据此得到的单独决策结果可能并不相容。虽然,陈彦等[11]将接车、发车作业进路和接入的到发线拼接形成列车过站径路,实现客运站到发线运用与作业进路编排的整体优化,但将调机出入段时间作为已知条件,而未考虑调机运用与其它作业间的相互影响。铁路客运站的调机运用优化问题,可描述为以调机作业接续里程和接续时间最小化为优化目标的指派问题,该问题在调机出入段时间和到发线运用方案确定的条件下是一个0-1 线性规划问题。本文在陈彦等[11]的基础上,以客站接发列车作业进路、调机运行进路和接续时间为决策对象,构建调机运用与列车径路安排综合优化模型及其模拟退火求解算法,实现了铁路客站接发列车作业进路排列、咽喉及到发线利用和调机运用的综合优化。
1 问题分析
设某繁忙铁路客运站始发、终到、通过列车集合分别为S,Z和G,列车集合I=G∪S∪Z,车底集合为C,到发线集合为W,道岔集合为V,客技线集合为U,列车i进入车站的作业为i(0),列车i离开车站的作业为i(1)。ti和t′i分别表示列车i需要占用到发线的开始和结束时刻,tc和t′c车底c∈C占用客技线的起止时刻。τi和τ′i分别表示列车i=S∪Z的车底出入段作业起止时刻,Q为车底在库内的标准作业时间,则有:

列车i∈I的进站端为o(i),出站端为d(i),o(i)与到发线w∈W之间共有n(o(i),w)条进路,其中第k条进路为到发线w与d(i)之间共有n(w,d(i))条进路,其中第k条 进 路 为为 进路上道岔v∈V的占用时长,且当时
对于b= 0,1,记作业i(b)所在咽喉区的道岔集为V(i(b)),和分别表示作业i(b)对道岔v的占用起止时刻,ei(b)v是表示作业i(b)是否会占用道岔v的0-1 变量,占用为1,否则为0,是表示作业i(b)是否会选择进路或的0-1变量,选择为1,否则为0。
对于列车i,j∈S∪Z,记τij为调机在列车i、j的车底出入段作业之间的接续时间,lij为相应的走行距离,J为规定的调机最小接续时间,L为客站与客技站之间的距离,则有:

式(3)中βij为0-1变量,若列车i和j同为始发或终到列车,其值为0,否则为1。
对于始发、终到列车和过路车,车站需要进行接发列车作业,并安排占用的到发线。对于始发终到列车,还分别需要进行车底入段和出段的调车作业。鉴于两者之间具有密切关系,可将其视为一个一体化协同优化问题,综合优化确定车底出入段作业的时间和列车过站径路。对于列车i,j∈S∪Z,可引入该问题的决策变量yij和ziw如下:


2 调机运用与列车径路安排综合优化模型
铁路客站的普速客车车底出入段的调机运用,需保证各车底出入段作业有且只有一台调机担当。因此,客车车底出入段调机运用的优化目标,可设定为调机出入段作业之间的接续时间和走行距离最小化。而旅客列车过站径路优化则是接发列车作业进路排列和到发线运用的综合优化问题[11],因此,可将调机运用优化问题视为车底出入段时间优化问题,结合文献[11]的旅客列车过站径路优化模型,可构建调机运用与客运列车径路安排综合优化模型。
2.1 约束条件
根据铁路客站行车技术作业特点,在综合优化模型中需考虑的约束条件主要有:
1) 列车接发车进路选择约束
办理列车i的作业i(0)时,需安排进站端oi至到发线w∈W间的一条接车进路,则

相应地,对列车作业i(1)时,需安排到发线w∈W至出站端d(i)间的一条发车进路,则
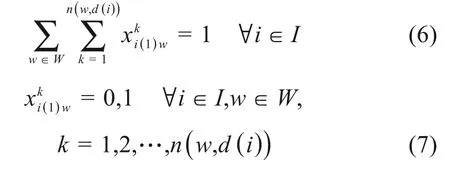
2) 车站到发线资源占用约束
作业i(0)与i(1)的接发进路决定了列车i的到发线占用情况,有

3) 车站咽喉道岔资源占用约束
作业i(0)与i(1)的接发列车进路决定了列车i的道岔占用,有:
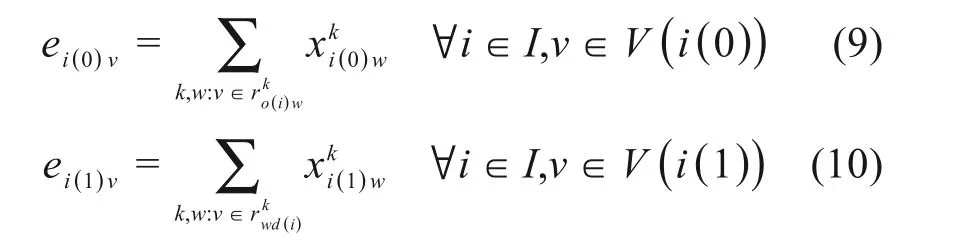
4) 车站咽喉道岔占用的时间约束
若列车i为通过和终到列车,则其到站时刻即可视为作业i(0)占用道岔v的开始时刻、占用到发线的开始时刻,即
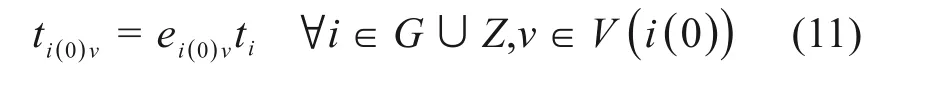
若列车i为始发列车,其作业i(0)占用道岔v的开始时刻为车底出库时刻,即
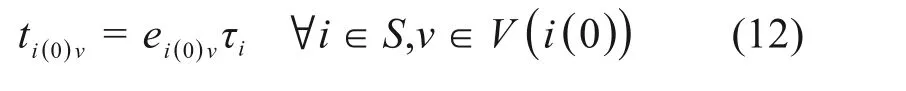
若列车i为通过和始发列车,则其发车时刻即可视为作业i(1)占用道岔的开始时刻和占用到发线的终止时刻,即
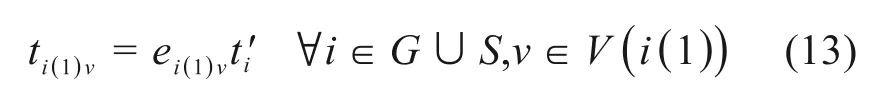
若列车i为终到列车,其作业i(1)占用道岔的开始时刻为车底入库时刻,即:
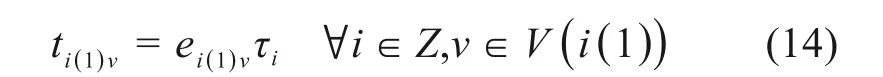
若列车i为通过和终到列车,其作业i(0)占用道岔的终止时刻由其选择的进路决定,即:
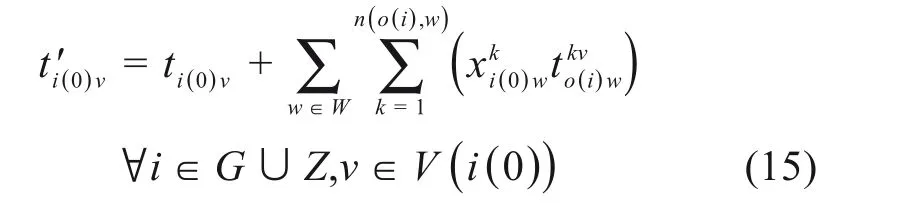
若列车i通过和始发列车,其作业i(1)占用道岔的终止时刻由其选择的进路决定,即:

5) 车站到发线资源占用的相容性约束
列车占用到发线资源具有时间上的排他性,同一时间最多只能被一列车占用,即

6) 车站咽喉道岔资源占用的相容性约束
作业进路占用道岔资源具有时间上的排他性,同一时间最多只能被一项作业占用,即

7) 到发线占用与车底出入段作业之间的时间接续关系
始发列车i的车底出库时刻与占用到发线的开始时刻对应,即

终到列车i的车底入库时刻与占用到发线的结束时刻对应,即

列车i的车底作业开始、结束时刻间的关系为
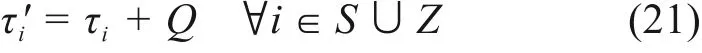
8) 车底出入段和客技线占用的时间接续关系
车底c的入库时刻为其占用客技线的开始时刻tc,即

车底c占用客技线的结束时刻t′c为其出库时刻,即

式中:αic为0-1变量,若列车i套用车底c,其值为1,否则,其值为0。
9) 车底在客技线整备作业的时长约束
车底占用客技线进行整备作业的时间不短于最小整备作业时间B,即
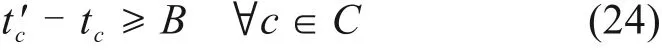
10) 列车在车站始发、终到作业的时长约束
始发列车在车站占用到发线的时间标准不短于最小始发作业时间D,即
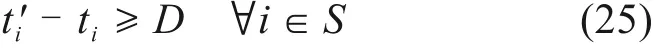
终到列车在车站占用到发线的时间标准不短于最小终到作业时间A,即
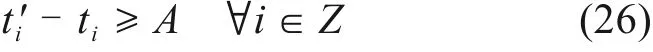
11) 调机牵引作业之间的接续关系约束
调机牵引作业的合理安排可被描述成一个指派问题,其约束如下:
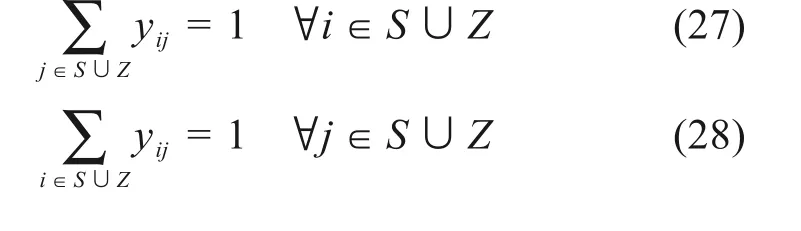
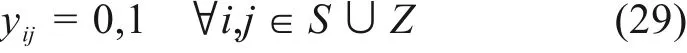
12) 调机牵引作业之间的接续时间约束
调机牵引作业之间的接续时间为:

2.2 目标函数
铁路客站的调机运用与列车径路安排综合优化,有以下调机牵引作业的总接续时间最少、调机牵引作业的总接续里程最短和车站到发线的利用效用最大等3个目标,分别为:

式(33)中ciw为列车i占用到发线w的效用,列车占用到发线符合固定使用方案则具有较高效用,到发线全日固定使用时间系扣除天窗并考虑一定空费后的纯占用时间,最大为1 122 min。
需要注意的是,该优化问题不一定具有可行解,当接发列车数量超过客站能力时,车站只能尽可能多地为列车安排过站径路,较高等级的列车优先安排。为此,将式(4)和式(6)分别松弛为
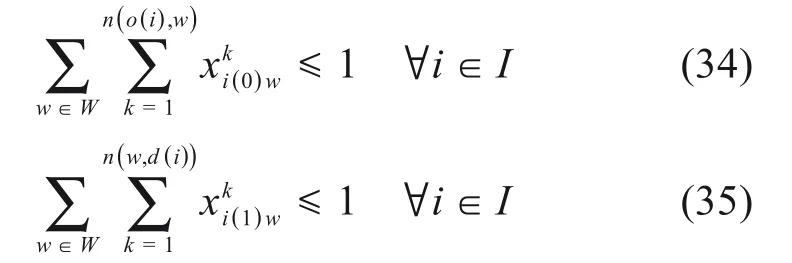
引入μ1,μ2,μ33个权重系数,将3个优化目标归一化处理,引入列车i的等级权重δi(等级越高,δi越大)和大的罚因子θ将约束条件(34)和(35)作为目标函数的一部分,也即有

由此,得到由优化目标(36)和约束条件(5),(7)~(30)构成的铁路客站调机运用与列车径路安排综合优化模型。
3 求解算法
由于模型的复杂性,本文选用模拟退火进行求解。依据问题的求解内容,设计的退火解由车底出入段时间方案和对应的列车过站径路方案构成,其中前一方案可表示为满足约束条件(19)~(26)的时间集合T={ti,t′j:i∈S,j∈Z}。以车底出入段时间方案T下的极大列车过站径路方案(J,X(J))作为列车过站径路方案,其中列车集J⊂I,X(J)为车底出入段时间方案T下满足约束条件(8)~(22)且不存在可行性扩展的

由此,模型的可行解可表示为(T,(J,X(J)))。
为尽量缩短始发、终到列车的到发线停留时间,设定ω为车底出入段的可行时间范围,限定始发列车i∈S的车底出库时间ti的取值范围为终到列车i∈Z车底入库时间的选择范围为,其中为始发列车i∈S的车底最晚出库时间,为终到列车i∈Z的车底最早入库时间。ω的取值必须满足车底整备最小作业时间要求,以保证车底出入段作业时间满足式(19)~(26)的要求。
(T,(J,X(J)))的邻域解有两种构造方法:第1种方法是从始发终到列车集合中任意选择k列车构成的列车集J′,重新为这些列车安排车底出入段作业时间得到新的车底出入段时间方案T′,然后在保持列车集J″=J-J∩J′的过站径路方案X(J″)不变的基础上,基于车底出入段时间方案T′寻找列车集及其过站径路方案使得构成新的极大列车进路方案,由 此 得 到 (T,(J,X(J))) 的 邻 域 解第2 种方法是从J中任意剔除k列车得列车集J͂,然后在保持车底出入段时间方案T和列车集J͂过站径路方案不变的情况下,寻找列车集͂及其过站径路方案使构成型的极大列车过站径路方案,由此得到的邻域解2 种邻域结构在退火过程中按等概率随机选用,以扩大搜索范围。为改善求解效率,采用变步长的温度下降机制。
4 算例分析
针对某既有线繁忙铁路客运站进行调机运用和列车径路安排方案优化,并与既有运营情况进行比对,以测试本模型与算法的优化效果。该客站站型如图1 所示,其中正线Ⅰ道和3,5 道用来接发下行方向的列车,正线Ⅱ道和4,6 和10 道用来接发上行方向的列车,8道为机车走行线,10道邻靠基本站台,客整所设有14 条供车底整备的客技线。该站目前全日接发列车总数为132列,其中停站通过100 列,始发、终到各16 列;在既有作业组织方式下,到发线办理能力利用率为84.8%、车站咽喉道岔通过能力利用率为79.2%,到发线和咽喉道岔能力均较为紧张。
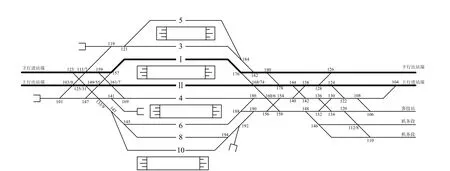
图1 某客站站型布局图Fig.1 Layout of a passenger station
车站所有进路均采用一次解锁,左、右两端咽喉道岔占用时间标准分别为1 min 和2 min。始发、终到列车的最小作业时间D和A均为25 min,同一条到发线先后接发列车的最小间隔为4 min,车底出入客整所作业的咽喉走行时间Q为10 min,最小的接续时间J按10 min考虑,最小整备作业时间B为5 h。目标函数中因子μ1=100.0,μ2,u3=10.0;惩罚因子θ=50 000.0,始发、终到列车的权重均取10.0,其他列车取5.0。
根据列车等级、方向及车站的到发线固定使用方案等因素确定各条到发线利用效用,见表1。
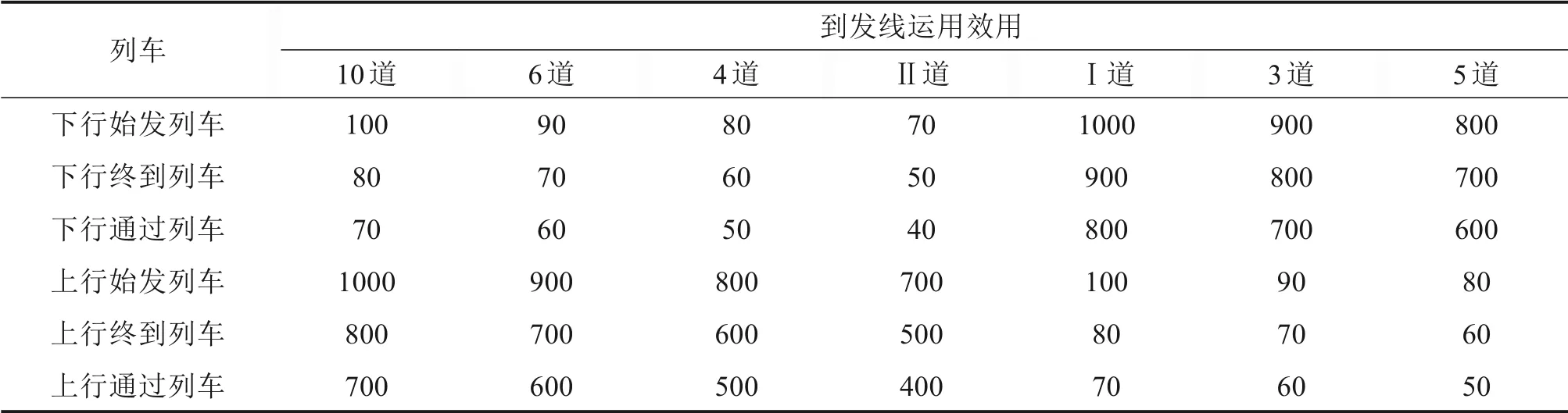
表1 到发线利用效用Table 1 Utility of arrival departure line
模拟退火计划的相关参数为:初始温度取200 000.0,初始的温度下降比例取0.9,温度低于10 时下降比例变更为0.5,每一温度下进行200 次迭代,算法终止条件为温度低于0.5或连续20次最优解无改变。
表2 给出了优化结果中部分列车的径路方案,车底出入段时间及到发线利用方案见图2和图3。
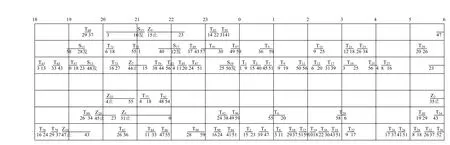
图2 18-6点到发线利用方案Fig.2 Utilization scheme of arrival departure line between 18-6 o’clock

图3 6-18点到发线利用方案Fig.3 Utilization scheme of arrival departure line between 6-18 o’clock
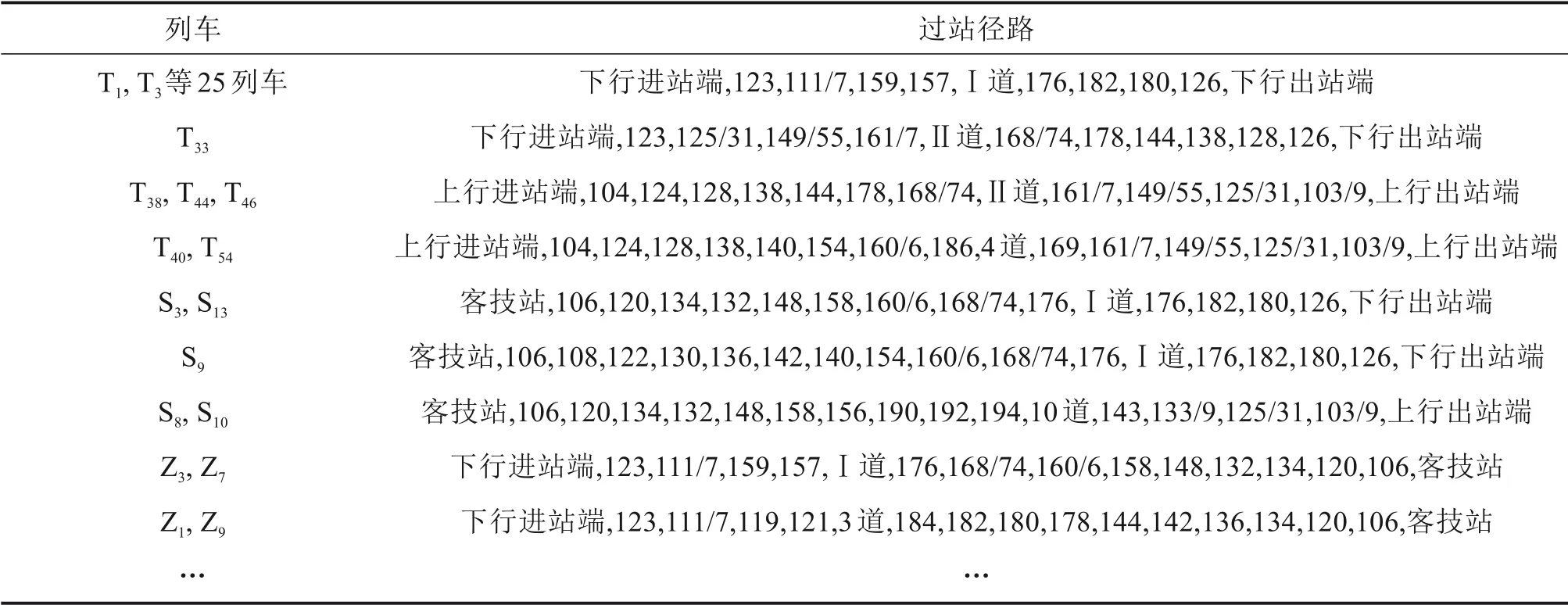
表2 列车过站径路方案(部分)Table 2 Train passing route scheme(part)
采用所提出的模型和算法对该客运站作业过程进行综合优化后,车站到发线、咽喉道岔的能力利用率分别降至70.7%和69.9%,可见,通过优化调机运用与列车径路安排,可有效缓解铁路客运站到发线和咽喉道岔能力紧张的情况。因此,前文所建立的模型和算法优化效果良好。
5 结论
1) 通过旅客列车过站径路优化建模,对接发列车作业进路排列与车站咽喉、到发线利用进行了一体化优化。
2) 将接发列车作业进路、车底作业进路和时间作为决策对象,把调机运用和旅客列车过站径路相结合,构建了调机运用与铁路客运站列车过站径路一体化优化模型,并基于模拟退火思想设计了该模型的求解算法。
3) 算例表明建立的模型可实现铁路客运站接发列车作业进路排列、咽喉及到发线利用和调机运用的一体化优化;求解算法运算快,结果合理正确,可为客运站的日常行车组织工作提供科学的决策依据。
