基于近似模型技术的高强钢盾构刀盘优化设计
2021-09-12闫利鹏黄鸿颖杨骁蔡鸿
闫利鹏,黄鸿颖,杨骁,蔡鸿
(1. 中铁建昆仑地铁投资建设管理有限公司,四川 成都610040;2. 西南交通大学 机械工程学院,四川 成都610031)
盾构机刀盘是直接与隧道开挖面岩土发生作用的关键部件,在盾构施工中刀盘和刀具受到较大的冲击和磨耗,对其结构的强度和刚度要求较高。成都地铁选用的土压平衡盾构机刀盘为普通刀盘材料,一般采用Q345C 钢,为满足刀盘在强度和刚度上拥有足够的安全余量,设计采用的钢板厚度大,导致刀盘面板的间隙空间不足;另一方面,工程上有时不得不采用带压换刀,带压换刀的安全性常常是困扰施工单位的难题,若将刀盘改为常压换刀设计,滚刀刀箱的布置就需要解决现有刀盘结构空间不足的问题;刀盘中心结泥饼也是成都地铁常见施工难题,需要增大刀盘中心开口率来解决,这一切都与刀盘的结构设计与材料有关。因此,刀盘结构设计时采用Q690 低合金高强钢材料,并在满足强度、刚度的条件下对刀盘进行结构优化,尽可能地减轻刀盘质量,同时增大刀盘中心开口率,对于解决上述困难问题,将是一项有意义的探索。目前,针对盾构刀盘的优化设计,国内已有研究并取得了一定成果。杨泊[1]以刀盘前面板和后面板的厚度作为设计变量,以最大等效应力、刀盘总质量以及总体变形作为目标函数,使用ave 环境的gdo 方法对刀盘进行了轻量化设计;田继涛等[2]以盾构刀盘的环形筋板尺寸作为设计参数,运用多目标遗传算法优化以提高刀盘的开口率;ROSTAMI 等[3]通过探讨盾构刀盘与围岩的关系,建立了针对硬岩环境条件的刀盘优化模型与方法;XIA 等[4]以强度和刚度为目标函数,采用多目标遗传算法求解盾构刀盘的优化模型。综上可知,针对盾构刀盘的优化设计主要是利用Ansys针对少数板厚变量进行优化;将主要结构进行力学分析从而建立优化数学模型进行优化等。现有研究所选变量较少,且耗时较长,效率有待提高,同时很少考虑从材料角度进行优化设计。针对成都地铁6号线某标段所用的土压平衡盾构机6.28 m 刀盘,本文基于刀盘最危险工况的受载情况,提出采用Q690 低合金高强钢代替原Q345C 刀盘的骨架结构材料并基于力学分析进行对比,分析2 种刀盘的优化空间。利用Ansys Workbench 对模型进行了参数建模、力学分析,然后集成Ansys Workbench 和Isight 对设计变量进行试验设计,并得到了不同参数条件下的样本点数据,由样本点数据拟合近似模型并进行优化,优化流程如图1所示。

图1 刀盘结构优化设计流程图Fig.1 Flow chart of cutter head structure optimization design
1 2 种材料刀盘静力学仿真结果的对比
采用Ansys Workbench 软件对比2 种材料刀盘在最危险工况下的静力学仿真结果,以此了解骨架材料为Q690的高强钢刀盘的“优化潜力”。
基于原成都地铁6.28 m 盾构刀盘的整体结构,对其骨架结构的材料进行等尺寸替换,由原Q345C 替换为Q690,包括刀盘的4 组辐条板、中心刀箱板、边滚刀箱板、外周圆环、环形支撑板、环形梁以及4 个云腿,结构材料更换部位如图2 所示,其中浅色部分材料为Q345C,深色部分材料为Q690。
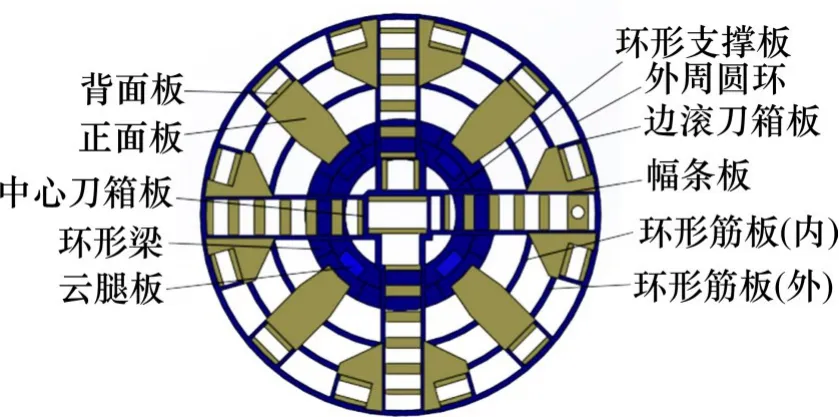
图2 高强钢刀盘三维模型Fig.2 3D model of high strength steel cutter head
由于盾构刀盘是一个非常复杂的模型,本文主要研究刀盘的整体骨架结构。因此为了提高软件的分析计算效率,对刀盘结构进行了部分简化,同时去除掉一些不影响计算结果的结构。简化后的模型中去除了所有的刀具,去除了倒角、螺栓孔以及泡沫注射孔等对刀盘整体结构影响不大的结构。刀盘模型采用正六面体网格为主导的划分方式,网格尺寸为30 mm,其平均精度为0.883 28,一般精度达到0.8即认为满足精度要求。
根据实际工程可知,刀盘在最大推力工况下有最大的位移量和应力,因此基于最大推力工况下的载荷对更换材料前后的刀盘施加边界条件,进行力学分析[5]。通过对原Q345C 刀盘在不同工况下的仿真分析可知,其在最大推力工况下的最大等效应力为192.03 MPa,主要集中在云腿与刀盘环形梁连接处,其值超过了Q345C 板厚80 mm 的许用应力,但是小于其屈服强度;采用Q690 材料替换后的刀盘在最大推力工况下的最大等效应力为230.75 MPa,也集中在云腿与刀盘环形梁连接处,其值低于Q690 的许用应力,且还有201.65 MPa的富余量,仿真结果如图3和图4所示。

图3 Q345C与Q690刀盘的等效应力分布Fig.3 Equivalent stress distribution of Q345C and Q690 cutterhead

图4 Q345C与Q690刀盘的总体变形分布Fig.4 Overall deformation distribution of Q345C and Q690 cutterhead
根据参考相关研究[6],本文取刀盘直径的3‰为许用变形量,即[δ]为18.84 mm,而原盾构刀盘在最大推力工况时有最大变形量2.331 6 mm,远小于许用变形量;采用Q690 材料替换后的刀盘在最大推力工况下的最大变形量为2.371 8 mm,也远小于刀盘许用变形量,两者变形量均有较大的富余。
综上可知,采用Q690 材料替换后的盾构刀盘在强度和刚度方面均有较大的富余量,相对原刀盘其更具“优化潜力”,可通过钢板厚度优化解决刀盘结构空间不足和提高刀盘中心开口率的问题。
2 刀盘结构优化设计数学模型
2.1 目标函数
本文以增大刀盘结构空间为目标,关键是优化减小各钢板的厚度,主要手段是在满足刀盘使用的强度刚度等安全条件下优化减小刀盘质量,因此以刀盘质量为目标函数,其表达式为包含所有结构尺寸变量与质量的函数:

式中:GM为刀盘质量,kg。
2.2 设计变量
为了提高高强钢刀盘“优化潜力”的利用率,设计变量的取值空间范围应尽可能大,根据工程经验并考虑到计算效率,结合刀盘自身特点和训练样本选取设定,针对刀盘结构的优化主要包括刀盘正面板、背面板、外周圆环、内外两圈环形筋板、辐条板、刀盘中心处4块刀箱板、环形梁以及刀盘的云腿等部位,优化的参数主要是各结构的钢板厚度。各变量的含义及取值范围如表1所示。

表1 刀盘结构优化设计变量Table 1 Design variables of cutter head structure optimization
2.3 约束条件
1) 强度和静刚度约束
以刀盘结构的强度和刚度以及结构尺寸作为直接约束条件。优化范围内的刀盘结构有2 种材料:Q345C 和Q690,因此在优化时针对不同材料的结构强度和刚度约束条件不同,具体表现在最大许用值的不同,如式(2)。

式中:变量m为Q345C 或Q690;δm(Xi),σm(Xi)分别为第i组设计变量对应的Q345C,Q690材料结构部分的位移量,mm;应力值,MPa;δmmax(X),σmmax(X)分别为Q345C,Q690 结构部分的最大位移量,mm 和 最 大 应 力,MPa;[δm]和[σm]分 别 为Q345C 和Q690 结构部分的位移许用量,mm 和最大许用应力,MPa;,分别为设计变量的下限值和上限值。
2) 几何尺寸约束
由于盾构刀盘结构形式非常复杂,不能直接计算刀盘的中心开口率,因此在保证刀盘整体外形尺寸不变的条件下,为了获得更大的中心开口率,对与其相关的结构尺寸进行约束,即:

3 近似模型与优化算法
3.1 样本点数据的试验设计
最优拉丁超立方设计是在随机拉丁超立方设计的基础上进行改进,所有的试验数据被尽量均匀分布在整个设计空间范围内,从而下一步利用合适的模型方法使得参数因子和相应输出之间的关系拟合更加准确而真实,为更高拟合精度近似模型的构建提供了更加有效的试验设计方法[7]。
为避免优化尺寸之间发生干涉,本文选取刀盘结构的35 个板厚参数作为输入变量,刀盘总质量和最大工况下刀盘的应力和位移作为输出响应值并进行试验设计。通过集成Isight 与Workbench软件,对变量进行最优拉丁超立方试验设计以保证试验数据选取的填充性,同时提高计算机仿真效率,得到的样本点数据用于近似模型的建立。
3.2 径向基神经网络模型的建立与误差分析
近似模型方法是一种可以将输入的参数因子与输出的响应之间的关系拟合为数学模型的计算方法。Isight 软件在近似模型模块中有克里格近似模型、正交多项式模型、径向基神经网络模型和响应面模型[8-9]。其中,径向基神经网络模型可以克服局部极小值问题并具有训练简洁、学习收敛速度快等优点。此外,通过多次对样本点进行不同近似模型的拟合,对比4 种近似模型的误差精度,刀盘优化的近似模型最终选择了径向基神经网络模型。
为了验证拟合后刀盘优化近似模型的精确性,需要对模型进行平均误差、最大绝对值误差、均方根误差以及可信度指标的误差分析。任意从试验数据中选取70 个样本数据进行误差的分析,以可信度指标(R2)为例,拟合的近似模型预测值与实际值的对比如图5所示,并得到了各项误差分析的结果如表2所示。

图5 可信度指标(R2)各项误差分析Fig.5 Error analysis of reliability index(R2)
由表2可知,本文拟合的径向基神经网络近似模型的(R2)大于0.9,其余各项误差均达到模型拟合精度要求,说明该近似模型具有较高的可信度。因此本文对刀盘的优化可以转化为对该近似模型相关变量的优化。

表2 各项误差分析结果Table 2 Results of error analysis
3.3 优化算法的选择
盾构刀盘的主体结构由上百块板件焊接而成,且各板件厚度不尽相同。本文对刀盘结构的优化主要集中在各钢板的厚度参数,且钢板的厚度参数是离散的,可得到本文优化参数的特点是:离散且数量较多。多岛遗传算法作为一种解决多参数变量、多目标函数或者在定义区间不连通的全局优化问题的算法,可避免部分情况达到局部最优解时就已经停止优化的发生,具有适应性强、优良的全局求解能力和较高的计算效率[10]。因此本文在Isight 软件提供的优化算法模块上设置多岛遗传算法,对第3节建立的高强钢盾构刀盘的优化近似模型进行刀盘轻量化的计算。
4 优化设计结果
在Isight 中得到精度达到要求的径向基神经网络模型后,将优化模块拖拽至任务框,选择多岛遗传算法进行优化计算,该计算过程主要是先随机选取一组随机变量(x11,…,x1n)并将其带入近似模型进行计算,得到相应的结果,然后与约束条件进行对比分析,根据对比结果以不同颜色标明,其中红色为不符合约束条件的数组。在第1组计算完成后又开始随机选取下一组变量,重复该过程直至得到各设计变量的最优解[11]。Isight 软件中算法相关参数的设置如表3所示。

表3 多岛遗传算法参数设置Table 3 Parameter setting of multi Island genetic algorithm
在10 000 次迭代运算后,在满足约束条件下各设计变量的最优解如表4。

表4 各设计变量优化结果Table 4 optimization results of design variables mm
根据优化后各刀盘结构尺寸建模,在最大推力工况下的静力学仿真结果分别如图6 和图7 所示。将Isight 软件优化结果与在Ansys Workbench中重新建模并计算的仿真结果进行对比如表5所示。

图6 刀盘整体等效应力和变形情况Fig.6 Equivalent stress and deformation of cutter head
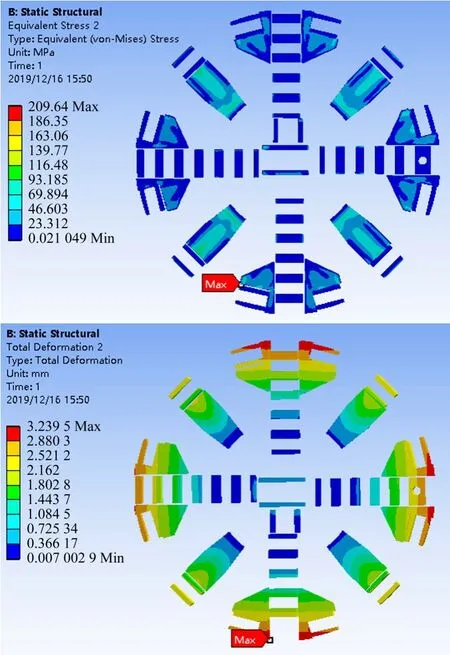
图7 高强钢刀盘的Q345C结构部分等效应力和变形情况Fig.7 Equivalent stress and deformation of Q345C structure
根据表5 可知,Isight 软件优化结果与Ansys Workbench结果的最大误差为4.096%,最小误差为0.2104%,两者误差不大说明采用Isight 优化的精度能够满足。
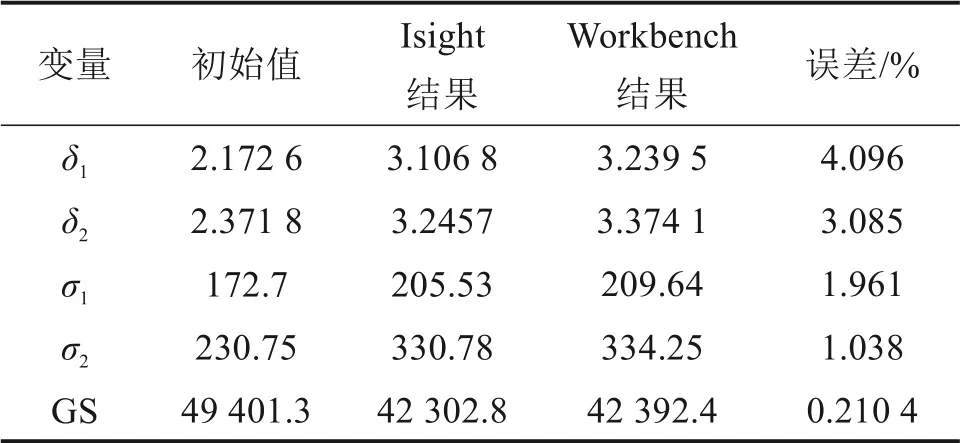
表5 Isight结果与Ansys Workbench结果对比Table 5 Results of error analysis mm
盾构刀盘对卵石“以排为主,以碎为辅”,例如在成都地铁1号线采用的某6.28 m 刀盘开口率只有28%,仅允许300 m 粒径卵石进入土仓,到18号线某8.6 m 刀盘的开口率采用45%的设计,可允许600 mm 粒径卵石进入土仓[12]。图8 为有关刀盘开口率与结泥饼的试验[13]。可见盾构设计思路为在满足安全原则下,应尽可能配置大开口率刀盘,可使卵石和渣土快速进入土仓,能有效减缓卵石滞磨和刀盘结泥饼现象,减少刀盘、刀具磨损,增加刀具寿命。

图8 刀盘结泥饼形态Fig.8 Mud cake shape of cutter head
优化后的刀盘相对原刀盘质量由49 401.3 kg减至42 392.4 kg,减少了约14.2%。同时通过对高强钢刀盘重新建模后测量发现,刀盘开口率由原来的35%增至约40%,刀盘中心开口率相较于原中心开口率增大了约8.6%,刀盘滚刀刀箱座的空间增大了约7.7%。因此,对普通钢盾构刀盘的骨架材料替换成高强钢,并进行优化设计以增大刀盘开口率是具有一定工程意义。
5 结论
1)由有限元分析结果可知,Q690 刀盘强度还有201.65 MPa 的富余量,变形量也有较大的富余量。因此,相较于常规Q345C 刀盘,替换材料后的高强钢刀盘具有更大的“优化潜力”。
2) 通过集成Ansys Workbench 和Isight 软件对高强钢盾构刀盘进行了优化设计,发现两者计算结果的最大误差为4.096%,满足精度要求;优化后的刀盘开口率增大至约40%,中心开口率相比原来增大约8.6%,刀盘结构的刀箱座空间增大了约7.7%,能有效解缓工程中卵石滞磨和刀盘中心结泥饼等实际问题。
3) 相对于其他优化方法,基于近似模型技术的优化方法能够优化离散且数量较多的试验参数,辨识出关键的试验因子,避免优化尺寸之间发生干涉,从而大大提高优化效率,节约时间。
