2万吨重载组合列车操纵优化研究
2021-09-11张益铭
魏 伟,张益铭
(大连交通大学 机车车辆工程学院,辽宁大连116028)
重载运输在世界货运铁路中占有重要地位,在世界各地发展方兴未艾。重载运输在我国铁路运输中发挥了重要作用。大秦和朔黄铁路圆满完成大运量运输任务,得益于2万t列车的开行,2万t列车在繁忙的大秦线和朔黄线发挥了重要作用。
2万t列车由于列车长、质量大、线路情况复杂,操纵十分困难,主要特点是车钩力大,列车运行安全性差,特别是中部机车脱轨和跳钩事故,使人们更加关注2万t列车操纵问题。很多重载铁路,2万t列车操纵指导书均是根据有经验司机的直观感觉制订,并参考了部分试验结果,以纵向动力学为主的理论还有很大空间应用到重载列车操纵优化中。
列车操纵优化一直是铁路货运的研究热点,张波[1]基于仿真和试验研究结果,完成了大秦线2万t重载组合列车操纵方法的完善和优化工作。温军刚[2]认为改变缓解地点、采取长波浪制动以及在较为缓和的线路纵断面缓解,可使重载列车操纵平稳。耿志修等人[3]证明重载列车在长大下坡道行驶,须在使用动力制动的同时仍必须多次施行空气减压的循环制动。董克毓等人[4]认为适当调节机车的电制动力并增加空气制动时间,能减少列车通过长大下坡道的制动次数。林轩等人[5]研究了货运列车在长大下坡道上的最优操纵策略和站间各子区间运行时间分配,提出长大下坡道及其相邻区间列车运行最优控制的数值求解算法,实现节能效果。葛学超等人[6]主要以货运列车节能观点出发研究列车操纵问题,将专家系统和节能运行最佳工况切换点判定准则相结合,设计了列车节能运行优化操纵算法。荀径等人[7]对以节能为目的的操纵优化方法进行了综述,指出解析方法能得到理论上最优解,计算速度快,但是需要对模型简化处理;仿真方法模型不需要简化,接近真实结果,是一种实用性较强的离线寻优方法。柏赟[8]经过仿真方法得出合理的控制列车区间运行速度上下限,可以节约行车能耗,从节能角度出发指出调速制动的关键是合理地选择制动初始点和缓解点。
目前货物列车操纵优化研究多数以节能为研究目的,平稳操纵研究较少,特别是以重载列车非常关注的车钩力为目标的优化工作开展较少,文中以某重载线路某长大坡道区段为例,研究2万t列车在此区段的操纵优化方法,并就操纵优化后可能存在的问题对机车自动制动机减压量显示准确度问题、制动减压量准确度问题、机车自动制动机评价指标问题和最小列车管减压量提出要求,为重载运输优化操纵提供借鉴。
1 列车纵向动力学仿真系统原理
在研究列车纵向动力学时,将列车抽象为一个多质点的质量弹簧阻尼系统。只考虑列车的纵向自由度。取某单一车辆(机车)为研究对象对其进行受力分析,如图1所示。
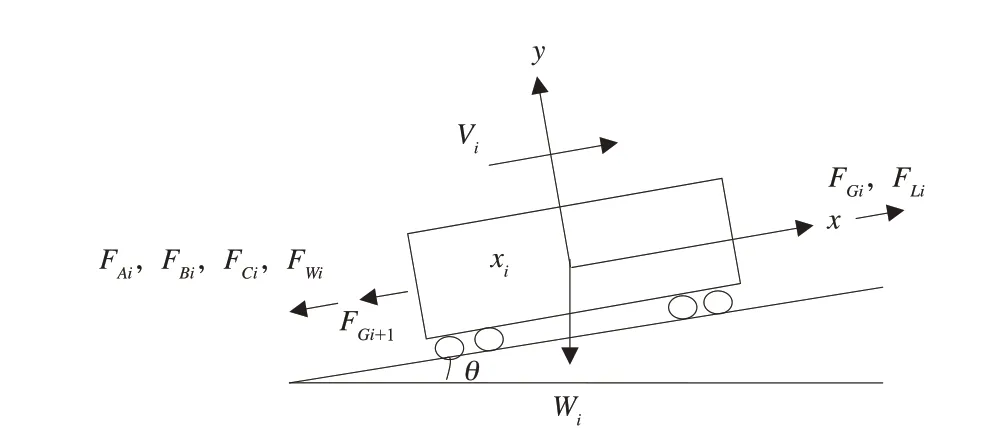
图1 单个车辆受力图
每个车辆(机车)力平衡方程为式(1)、式(2):
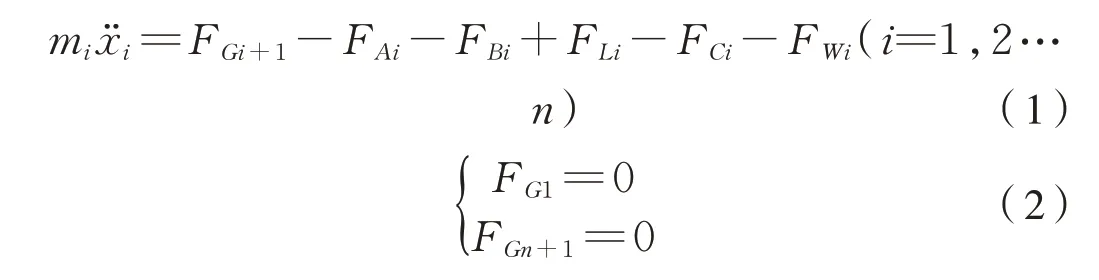
式中:n为列车中包含的机车车辆总数;miẍi为第i节车的惯性力;FGi、FGi+1分别为第i节车前、后钩的车钩力;FAi为第i节车运行阻力;FBi为第i节车空气制动力;FLi为牵引力或动力制动力;FWi为第i节车所受的坡道阻力;FCi为第i节车所受的曲线阻力。
因为列车编组的差异性以及制动系统减压种类的多样性,列车制动系统特性千差万别,而列车制动系统特性对列车纵向冲动起决定性作用,特别是缓解前和制动前制动系统的压力分布,将直接影响后续缓解动作的传递过程和非首次制动的制动能力。因此为了获取这种随制动减压量、时间和漏泄等多种因素影响的制动系统特性,研究制动系统特性的获取采用基于气体流动理论的列车空气制动仿真系统实现[9]。该仿真系统根据气体流动理论计算瞬态气体压强,再根据分配阀原理计算每一个分配阀的动作过程以及瞬时气体通路,具备连续模拟制动系统动作过程的能力。影响车钩力的另一重要因素是缓冲器模型,该仿真系统中缓冲器模型采用基于列车运行试验方法获得的缓冲器轮廓线模型。
2 列车空气制动与纵向动力学联合仿真系统
文中使用基于气体流动理论的空气制动仿真系统和基于多体动力学的列车纵向动力学仿真系统,该仿真系统具有空气制动和纵向动力学同步仿真功能,在仿真计算过程中可以实时显示车钩力、制动系统压强、加速度沿车长分布,直观了解车钩力产生过程。该仿真系统的最大特点是可以随时动态计算制动系统压强,因此能准确表述制动力变化以及缓解过程中不同时刻充风状态的变化,保证了仿真系统中制动系统压强变化与真实列车制动系统压强变化一致,能够更真实地反映不同时刻制动和缓解时制动系统内真实的压强分布规律,以及这种压强分布对制动和缓解的影响[10-12]。该仿真系统参加了国际纵向动力学评测,在计算精度和计算速度上获得优异成绩[13]。
3 操纵仿真及优化结果
某重载铁路,全长594 km,全线海拔高度差1527 m,受坡道多、曲线多、分相点和地形复杂等多种因素影响,2万t列车操纵难度较大。该段线路起始地点为K20+400,终止地点为K34+881,下坡道坡度分别为10.2‰、10.8‰、12.0‰、10.7‰、12.0‰。目前的操作方法是配合电制动的4次循环空气制动,主要问题是C地点和D地点所在的位置是长度为12800 m,下坡道坡度为10.2‰的隧道,在这2处地点缓解时车钩力较大,某次2万t列车(编组为1HXD1+108C80+1HXD1+108C80+可控列尾)实际操纵指令(包含空气制动、电制动指令)及对应的速度曲线如图2所示,A-E分别为列车制动或者缓解时易产生较大车钩力的困难地点,最下方相对海拔高度线上每一个小竖线代表一个变坡点。
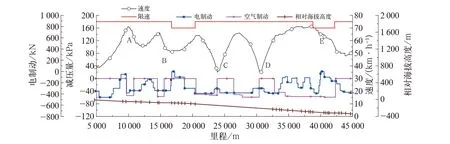
图2 列车操纵指令和速度图
初始时列车位于K5+000处,初速度约为40 km/h,在下坡作用下,列车速度不断增加,在约69 km/h时越过A地点,此时开始减压50 kPa制动,并施加340 kN的电制动力,列车速度开始下降,在速度约63 km/h时开始缓解,缓解后速度最低降到56 km/h;在坡道的作用下列车速度再次上升,当速度达到约65 km/h时施加减压50 kPa制动,电制动力为340 kN,速度降低到57 km/h时缓解,此时经过B地点,缓解后列车速度还在降低,速度最低达到51 km/h;其后因为坡道原因列车速度再次上升,当速度达到64 km/h时第3次施加空气制动,当速度降低到36 km/h时开始缓解,此时列车运行在C地点;速度上升到65 km/h施加第4次空气制动,当速度降低为36 km/h时再次缓解,到达D地点。从A地点到D地点共有4次制动缓解过程,即“四把闸”。该列车通过困难区段最大车钩力曲线如图3所示,其中最大拉钩力发生在109车位(包含机车的序号),即中部机车前钩位,最大拉钩力值为995 kN;最大压钩力发生在125车位,位于中部机车后部的车辆中,最大压钩力值为1077 kN。中部机车前后钩车钩力时域图如图4所示,由图4可知,列车通过C地点和D地点缓解会产生较大的车钩力,其中在C地点缓解产生的拉钩力是列车通过此区段产生的最大拉钩力。
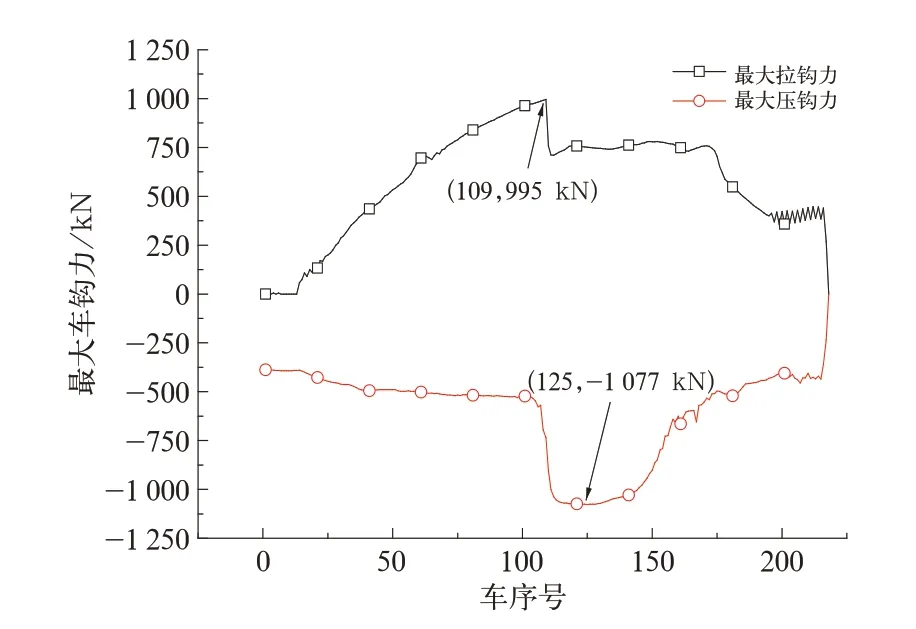
图3 列车通过困难区段最大车钩力分布曲线

图4 中部机车通过C地点和D地点车钩力曲线
在列车操纵过程中,列车管减压量通过机车制动装置显示仪表显示,该显示的跳动量为10 kPa,几次初减压量制动机车显示的制动减压量均为50 kPa,而根据机车BCU采集的数据,真实的列车管减压量均为59 kPa,仿真时根据机车BCU数据施加制动指令。
为了避免C地点和D地点制动及缓解过程中较大车钩力产生,对整个列车操纵过程进行了优化,其基本原则是尽量减少空气制动循环次数,特别是避免C地点后空气制动的施加。为此,在A地点处施加的空气制动增加制动时间,以保证第一次制动后具有较低的列车速度,根据反复仿真操纵,确定当A地点处制动时,待速度降低到58 km/h时才开始缓解,相对于原操作,缓解速度更低,大约低5 km/h,此速度下缓解的同时施加较大的电制动力,使列车速度缓慢增长,可以保证列车在B地点前不再制动,此时施加的最大电制动力约为380 kN。越过B地点后在约K20+000处,速度上升到约64 km/h,低于限速的70 km/h,此时施加减压50 kPa的空气制动,同时在此区间尽量使电制动小一些,这一把闸基本上能保证列车速度缓慢上升,直到K32+070时速度达到68 km/h略微增加电制动,使速度逐渐下降,安全越过E地点(分相)。此种操作方法使原来四把闸空气制动减少为两把闸空气制动,特别是避免了C地点和D地点的缓解过大车钩力的产生。制动指令和列车速度变化图如图5所示,为了便于比较,原来操纵方法的速度图也一并画出。
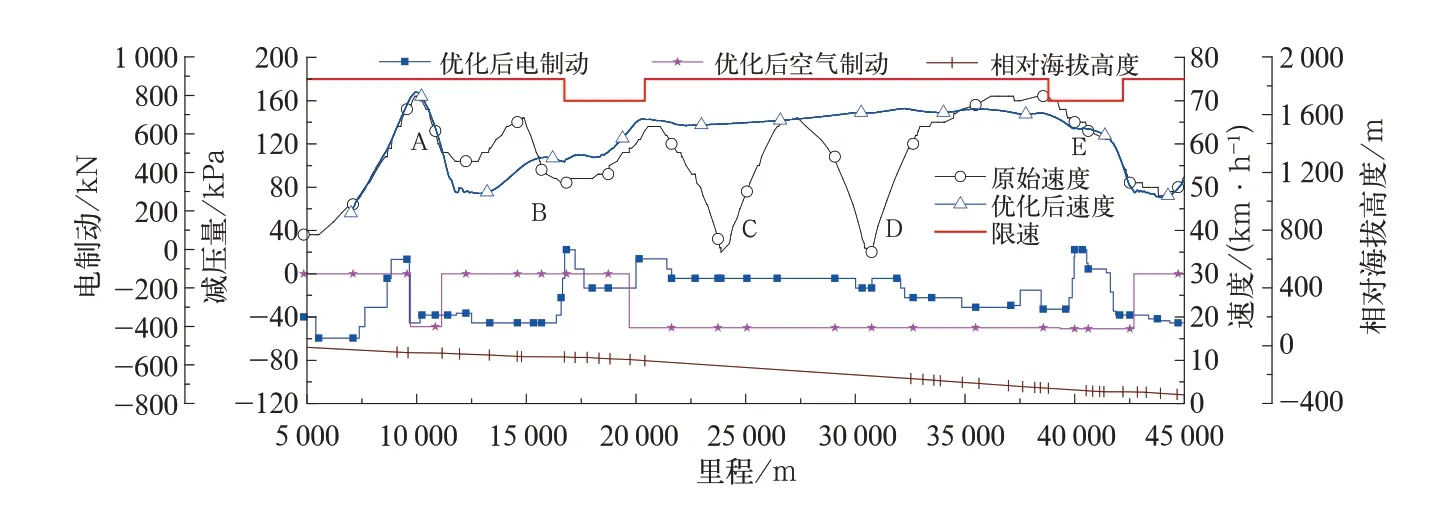
图5 优化后指令和速度
上述操纵方法的特点是在C地点和D地点间实施一把闸操纵,即使用一次长时间制动,确保列车速度上升很慢,仅在E地点通过以后施加缓解,因此避免了C地点和D地点的2次制动,进而避免了C地点和D地点缓解产生过大的车钩力。按上述操纵方法通过此区段最大车钩力分布如图6所示,最大拉钩力和压钩力值分别为676 kN和954 kN,较优化前分别减小32.1%和11.4%。优化后最大车钩力产生的位置在A地点制动缓解后,中部机车前后钩车钩力值如图7所示。
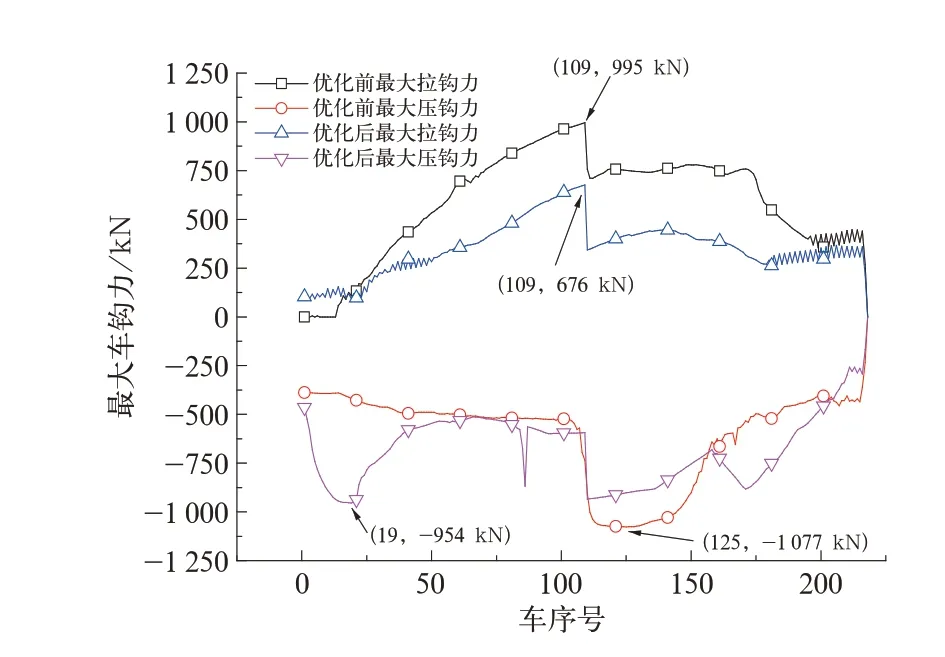
图6 优化前后列车通过困难区段最大车钩力分布曲线
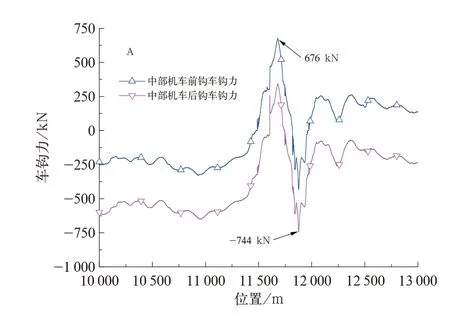
图7 中部机车通过A地点车钩力曲线
上述操纵方法的难点在于K20至K32+070的速度缓慢上升,其核心是具有较小的制动力,即小的空气制动力和电制动力。目前制动系统设计是电制动优先,因此在空气制动时一定具有电制动力,这时的电制动力可以调整到机车可施加的最小电制动力48 kN。在这个制动过程中空气制动力占制动力的主要部分,因此空气制动力在保障上述操纵方法中具有决定性作用,即空气制动必须准确减压,并且能够保证空气制动减压量不大于50 kPa。
上述操纵方法经与现场有经验司机交流,少量列车能够完全按照此方法操纵,大部分列车因为制动力过强的原因,无法实现在K20至K32+070区段的速度缓慢上升,制动力强的主要原因是制动减压量不准以及减压量显示不准。
目前列车空气制动仿真系统设计按最小减压量40 kPa设计,新设计HXD系列机车电控自动制动机最小减压量是50 kPa,但是根据目前机车自动制动机的检测指标,仅对均衡风缸减压速度和减压量有要求,而自动制动机最终控制的列车管减压量没有明确要求,因此常常出现机车均衡风缸减压准确,但是列车管减压不准确,并且列车管减压量偏大的问题。现场中有些机车很难实现减压50 kPa空气制动,一般情况是实际减压量明显大于50 kPa。假设此列车在K20处减压50 kPa空气制动而实际减压量为53 kPa时,电制动力调整到最小48 kN,根据仿真结果,列车速度明显降低,将在K32+500处停车,无法到达E地点,速度对比如图8所示。如要避免停车,列车只能按照原来的操纵方法,当速度降低到35 km/h时开始缓解,此时的缓解位置与C地点和D地点均在同一坡道上,依然会产生较大车钩力,因此上述操纵方式在机车减压量过大和减压量不准的情况下很难实现。
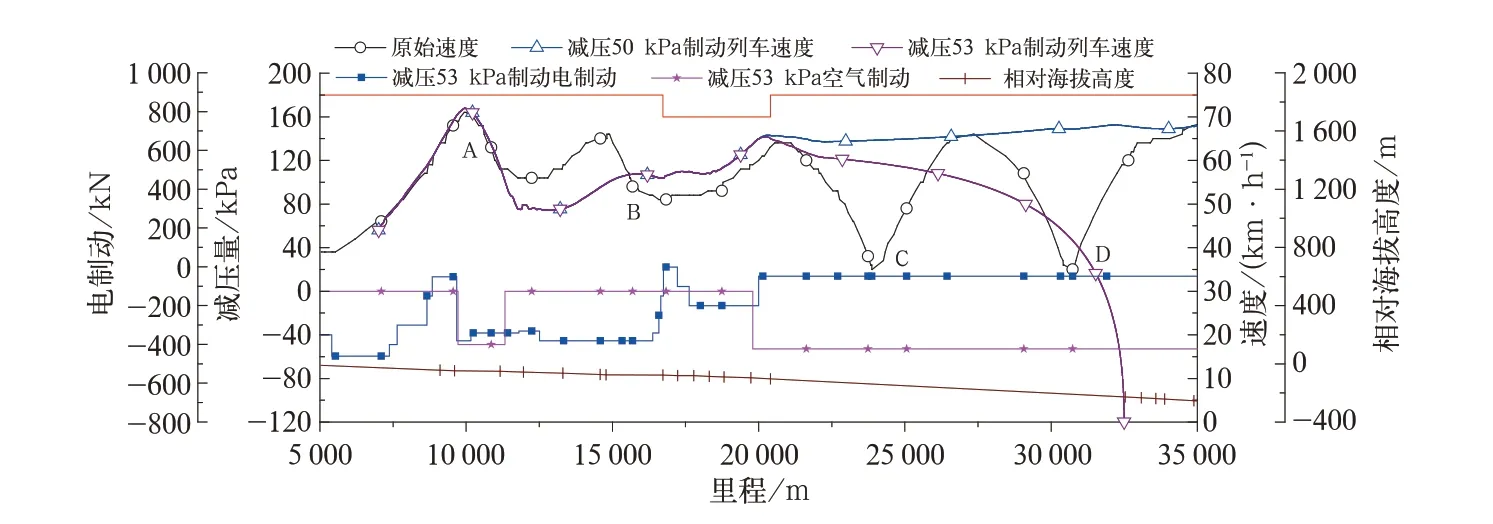
图8 减压量改变后列车速度比较
4 有关操纵的难点分析
4.1 制动减压量显示精度问题
现有重载列车机车制动减压量显示精度为10 kPa,例如初减压时显示值是50 kPa,实际上最大列车管减压量可能为59 kPa,如上面真实列车的运行算例,而不同的机车减压量可能也有所不同,在初减压时可能最小的减压量小于50 kPa,也就是说机车上显示的减压量和真实减压量有较大差异。同样的显示减压量,因为实际减压量不同,列车的制动能力存在明显差异,在司机不清楚真实减压量情况下,仅凭司机的感受操控列车难度可想而知,因此提高机车减压量显示精度是优化操纵的前提。
4.2 制动减压量控制精度问题
制动减压量直接影响到列车制动能力,进而影响到列车的控制能力。相同减压量手柄位置,每次实际减压量都有所不同,这是目前重载列车中普遍存在的问题,同一制动手柄位置,列车管减压量差异最大可能达到9 kPa,这加大了重载列车操控难度,对于初制动,相当于减压量偏差近18%,这么大减压量差异的情况下,制订出的操纵方法可塑性空间很小,几乎没有操纵优化余地,因此需要提高减压量精度,增加操纵可行区间。
4.3 机车减压量控制目标问题
列车制动能力是以列车管减压量为衡量标准,因此说列车自动制动机最终的控制量应该是列车管的最终减压量。目前机车自动制动机检查标准中仅要求控制均衡风缸的减压速度和减压量,而均衡风缸仅是自动制动机的中间环节,对于最终控制目标,即列车管减压量和减压速度没有明确标准,仅有列车管压强跟随均衡风缸压强变化的粗略要求,因此会出现均衡风缸减压速度和精度完全满足标准要求,但是最终的列车管减压量和减压速度千差万别,对于短编组列车,因为列车操纵方法可塑性较大,减压量偏差不会带来什么问题,但是对于重载列车,操纵可用区间很小,因此需要精确控制。建议重载列车用机车自动制动机增加对列车管减压速度和减压量的标准要求。
5 结论
经过仿真系统计算和重载列车运行经验,长大重载列车有优化操纵空间,同时在实现操纵优化时需要对机车自动制动机提出要求。
(1)重载列车在长大坡道可以通过仿真方法进一步优化操纵过程,以某重载铁路某区段为例,循环制动可以由4次减少为2次。易产生较大车钩力的地点可避开,最大拉钩力和压钩力分别可减小32.1%和11.4%。
(2)重载列车操纵优化的前提是列车必须能够实现空气制动的精准控制,因此建议提高机车减压量显示装置的精度;提高机车自动制动机减压量准确度;机车减压量应该以真实的列车管减压量为控制目标,而不应该以均衡风缸减压量为控制目标,机车自动制动机需要实现列车管最小减压量50 kPa的目标。
