无人机固定时间路径跟踪容错制导控制
2021-09-11崔正阳王勇
崔正阳 王勇
(1. 北京航空航天大学 自动化科学与电气工程学院, 北京 100083; 2. 北京航空航天大学 无人系统研究院, 北京 100083)
近年来,无人机在环境监测、军用侦查、灾后搜寻及救援[1-3]等应用场景下发挥着重要的作用。 作为一个灵活机动的战术应用平台,无人机的路径跟踪控制引起了世界各国科研团队的关注[4-6],其中无人机对未知干扰和执行机构故障的鲁棒性、状态误差限制以及跟踪误差收敛性能在路径跟踪控制研究中具有重要意义。 视线(Line-of-Sight)制导控制算法作为一种有效的制导算法,在路径跟踪领域有着广泛的应用[7-10]。制导算法利用参考轨迹和无人机运动状态计算得到姿态指令,通过控制回路实现无人机对参考轨迹的跟踪。 文献[11]证明了视线导引律的一致半全局指数稳定性;文献[12]提出了自适应视线导引律,通过对侧滑角的自适应估计补偿提升系统性能,能够确保系统全局一致稳定;文献[13]利用侧滑角观测器进行状态估计,确保系统误差在具有外部干扰的情况下有限时间收敛。
无人机利用视线制导控制算法进行路径跟踪的过程中,系统状态误差的收敛时间是一个比较重要的指标,直接影响路径跟踪的快速性。 文献[11-13] 中的系统均为指数稳定或有限时间收敛稳定。 系统有限时间稳定虽然与指数稳定相比能够确保收敛时间为有限值,但是该收敛时间依赖系统初始状态,在初始条件不确定的情况下会严重影响系统性能。 文献[14]提出了固定时间收敛的概念,使系统收敛时间的上界不依赖于初始状态,具有更好的工程应用价值。 本文针对无人机路径跟踪控制问题进行研究,提出固定时间收敛的视线制导控制算法,确保跟踪误差收敛时间不依赖系统初始状态。 另外,为了确保跟踪控制过程中偏航角不发生剧烈变化,实现无人机的安全飞行,系统需要对角速度误差进行限制。 特别是太阳能无人机的机翼通常为具有大弦比的柔性结构,较大的偏航角速度会引起机翼的抖动,并产生额外的滚转力矩威胁无人机的飞行安全[15]。 本文综合考虑上述问题,实现无人机跟踪误差在固定时间内收敛的同时,保证对角速度误差的有效限制。
系统不确定性、外部环境干扰、执行机构故障等因素会严重降低无人机路径跟踪的控制精度及稳定性,但是未知干扰值通过传感器很难进行精确测量。 同时,如果对执行机构故障不及时进行处理会导致系统性能迅速恶化甚至任务失败。 其中,由于大翼展柔性太阳能无人机存在气弹问题,很难对其构建精确动力学模型,这就使得系统不确定性对系统稳定性的影响显得格外突出[16]。扰动观测器是一种广泛应用的对干扰及故障进行快速精确估计补偿的方法,并且取得了诸多研究成果[17-20]。 为了实现无人机固定时间路径跟踪制导控制,需要在固定时间内精确估计补偿干扰及执行结构故障,确保系统具有良好的路径跟踪控制性能。
综上所述,在综合考虑未知干扰及执行机构故障等因素影响的情况下,实现无人机路径跟踪误差的固定时间收敛,并同时保证对角速度误差的限制是本文的研究重点。 研究工作的主要内容如下:首先,本文提出一种视线制导控制算法框架,对无人机进行制导控制一体化设计,确保整个闭环系统跟踪误差满足固定时间收敛,并且该收敛时间与系统初始状态量无关。 其次,同时考虑外部干扰及执行机构故障等因素的影响,实现对未知干扰在固定时间内进行估计补偿,确保无人机具有良好的容错性和鲁棒性。 同时,对偏航角速度误差进行限制,使系统状态平滑变化。 最后,通过仿真算例证明,本文算法在具有更快的收敛速度和更高的控制精度的同时,具有良好的鲁棒性。
1 问题描述

式中:mr为航向转动惯量;dr为阻尼常数;τf为力矩控制量;τr为具有执行机构故障的控制量;τd为未建模参数不确定性和外部干扰;τfd为总干扰;本文假设干扰值及其微分项有界,该执行机构故障模型τaf同时包括了乘性故障和加性故障。kfd为加性故障;kf为损失的舵效比,当该值为0 时表示执行机构完好,当该值为1 时则表示该执行机构完全损坏。 本文假设干扰值及其微分项有界,同时无人机存在独立设计的高度、滚转角及速度稳定控制回路。
路径跟踪动态特性表示如下:

式中:e为侧向跟踪误差;ψe为偏航角与期望航迹角的偏差角度;χ为期望航迹角;κ为期望路径的曲率。
图1 表示了无人机路径跟踪控制过程中状态量之间的几何关系。 图中:U为无人机合速度,u为前向速度。

图1 无人机路径跟踪控制几何示意图Fig.1 Path following control geometry of an UAV
本文的控制目标为设计相应的容错制导控制算法,确保无人机存在执行机构故障及未知干扰的情况下,系统跟踪误差满足固定时间收敛,并且该收敛时间与系统初始状态量无关。
注1 本文采用偏航角控制子回路对侧向跟踪误差进行控制,该控制结构在以太阳能无人机为代表的大翼展飞行器中有着广泛的应用。 同时,本文提出的控制结构和设计方法也可推广应用到利用滚转角控制子回路对侧向跟踪误差进行控制的情况。
2 固定时间收敛的视线制导控制算法
视线制导控制算法的构成如图2 所示,主要包括路径跟踪制导回路和偏航角控制子回路,ψc为期望偏航角指令。 路径跟踪制导回路计算得到期望偏航角指令信息,输入至偏航角控制子回路。偏航角控制子回路通过自然指数障碍李雅普诺夫函数对偏航角速度误差进行限制,同时利用固定时间扰动观测器,确保系统对外部干扰和执行机构故障具有良好适应性的同时,保证侧向跟踪误差及偏航角误差在固定时间内收敛。

图2 视线制导控制算法框架Fig.2 Framework of path following guidance control algorithm
引理1[14]假设存在如下系统:

2.1 固定时间扰动观测器设计
无人机在飞行过程中受到外部环境干扰,气动参数不确定性,执行机构故障等因素影响会使得飞行性能急剧恶化。 本文引入固定时间扰动观测器对外部干扰及执行机构故障等不确定性扰动进行在线估计补偿,确保扰动估计误差在固定时间内收敛,从而增强系统的鲁棒性。 由式(2)、式(5)可得

针对式(9)、式(10)所示系统设计固定时间扰动观测器,确保非线性扰动项fe、fr的估计误差在固定时间内收敛,固定时间扰动观测器设计如下:

对式(11)、式(12)进行整理,得出如下观测器状态估计误差:

式中:δ1=^e-e;δ2=f^e-fe;δ3=^r-r;δ4=f^r-fr;q1> 0;l1h-1(l1)>l3-L1,h(l1)= 1/l1+ [5.436/(l1l3-l1L1)1/3];l3>L1;l2> 0;q2> 0;l6>L2;l4h-1(l4)>l6-L2;l5> 0;h(l4)= 1/l4+[5.436/(l4l6-l4L2)1/3];l1、l2、l3、l4、l5、l6、q1、q2为需要设计的观测器参数,收敛时间由观测器参数决定。
根据文献[20]中Theorem 1 得到的结论,δ1、δ2、δ3、δ4能够在固定时间TL1、TL2内收敛到0,即干扰估计值f^e、f^r能够分别在固定时间TL1、TL2内估计非线性干扰项fe、fr。

2.2 路径跟踪制导控制一体化设计
视线制导控制算法设计的目标是对路径跟踪制导回路进行一体化设计,使无人机的路径和偏航角跟踪误差在固定时间内收敛,同时偏航角速度误差满足给定的限制条件。 对式(2)、式(5)进行整理后,可得
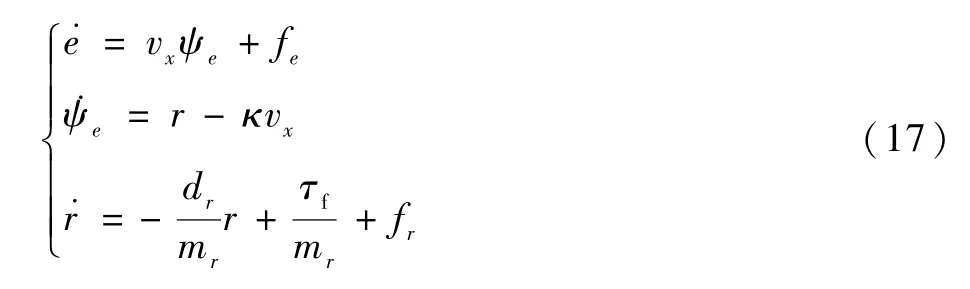
图3 为视线制导控制算法模块。 滤波器输入为虚拟控制量α1和α2;ψc和̇ψc、rc和̇rc为期望偏航角和偏航角速度指令及其导数;ξ1和ξ2为误差补偿量。 本文对路径跟踪制导回路和偏航角控制子回路进行一体化设计,利用固定时间扰动观测器实现对未知干扰及执行机构故障进行估计补偿。 在路径跟踪制导回路中,制导指令生成器根据期望路径信息计算出制导回路虚拟控制量,通过指令滤波器获取期望偏航角指令及其导数,利用误差补偿器对指令滤波器引起的误差进行补偿。 在偏航角控制子回路中,通过反步法将期望偏航角指令输入至姿态角回路控制器,经过指令滤波器和误差补偿器后,将期望偏航角速度指令输入至动力学控制器。 动力学控制器输出考虑偏航角速度误差限制的控制量,最终实现对无人机的路径跟踪制导控制。 通过视线制导控制算法设计能够确保整个路径跟踪制导控制系统在固定时间内收敛。

图3 视线制导控制算法模块Fig.3 Block diagram of light-of-sight guidance control algorithm
路径跟踪制导回路虚拟控制量设计如下:

式中:ηf1、ηf2、ξ11、kξ11为设计参数;ξ1为误差补偿值;z1=e-ed为路径跟踪误差;ed=0 为期望路径跟踪误差;c11>0,c12>0,kξ11>0。
为了避免在反步法中对虚拟控制量的导数进行复杂计算,本文设计了指令滤波器,滤波器输入为虚拟控制量α1和α2,输出为期望偏航角和偏航角速度指令ψc、rc及其导数,指令滤波器表达形式如下:
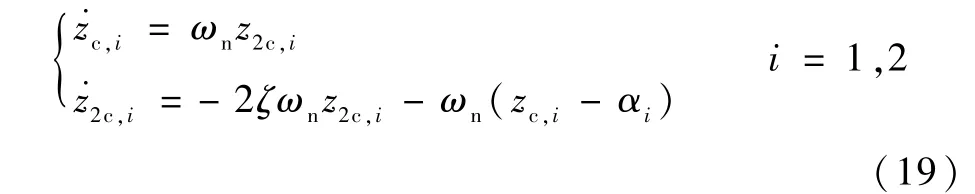
式中:(zc,1,zc,2)= (ψc,rc);ζ和ωn分别为阻尼比和频率,ζ=0.8、ωn=45。 指令滤波器的估计误差分别为Δα1=ψc-α1、Δα2=rc-α2。
由于指令滤波器存在估计误差Δα1、Δα2,需要引入误差补偿器对该估计误差进行补偿以消除其对系统控制精度的负面影响。 误差补偿器设计如下:


由式(29)可见,在没有状态限制条件的情况下,自然指数障碍李雅普诺夫函数能够退化为二次型形式进行稳定性分析。
力矩控制量τf设计如下:

定理1 利用式(11)、式(12)设计的扰动观测器,采用式(18)、式(24)、式(30)设计的控制规律,则系统(17)在固定时间内收敛。
证明 根据式(21)、式(26)、式(28)的李雅普诺夫函数,选取如下李雅普诺夫函数:

由于扰动项fe和fr均采用固定时间扰动观测器进行估计,即εe、εr均能够在固定时间内收敛到0。 当t> max(TL1,TL2)时,从式(35)推导可得

3 仿真分析
为了验证本文算法的有效性,利用文献[23]的无人机模型进行路径跟踪仿真试验,文献[13]提出的有限时间控制算法作为对比分析算法。 本文参数取值如下:c11= 0.05,c12= 0.06,ηf1=0.9,ηf2= 1.5,c21= 0.5,c22= 0.6,c31= 0.6,c32=0.5,kr= 0.5,kξ11= 0.01,kξ22= 0.01,q1=q2= 2,l1= 10,l2= 2,l3= 2,l4= 70,l5= 14,l6=700,kΔ1=kΔ2= 0.1,εξ1=εξ2=εr= 0.01,ζ= 0.8,ωn= 45。


图4 路径跟踪效果Fig.4 Path following performance

图5 侧偏距离误差Fig.5 Cross-track errors
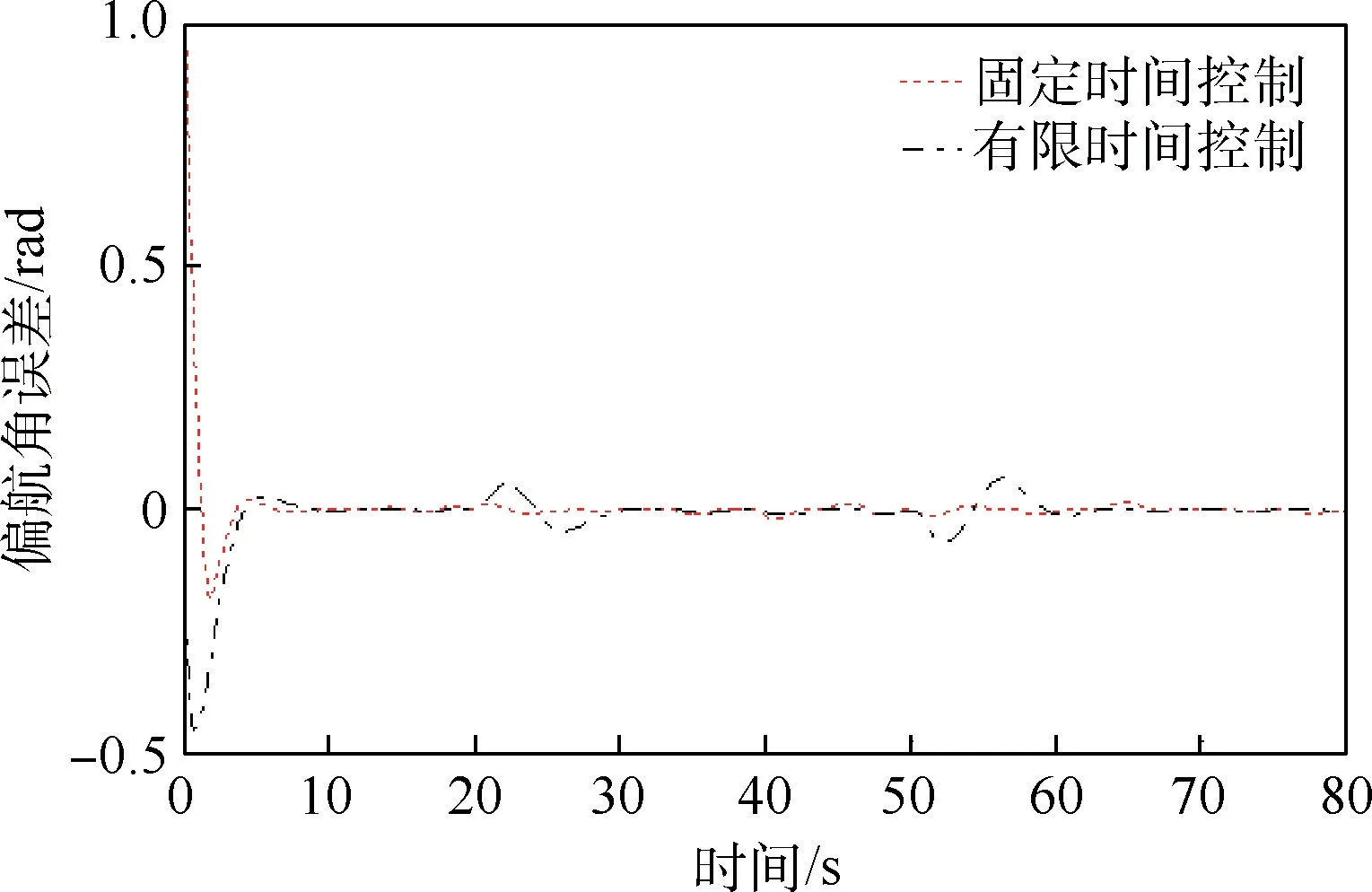
图6 偏航角误差Fig.6 Yaw angle errors
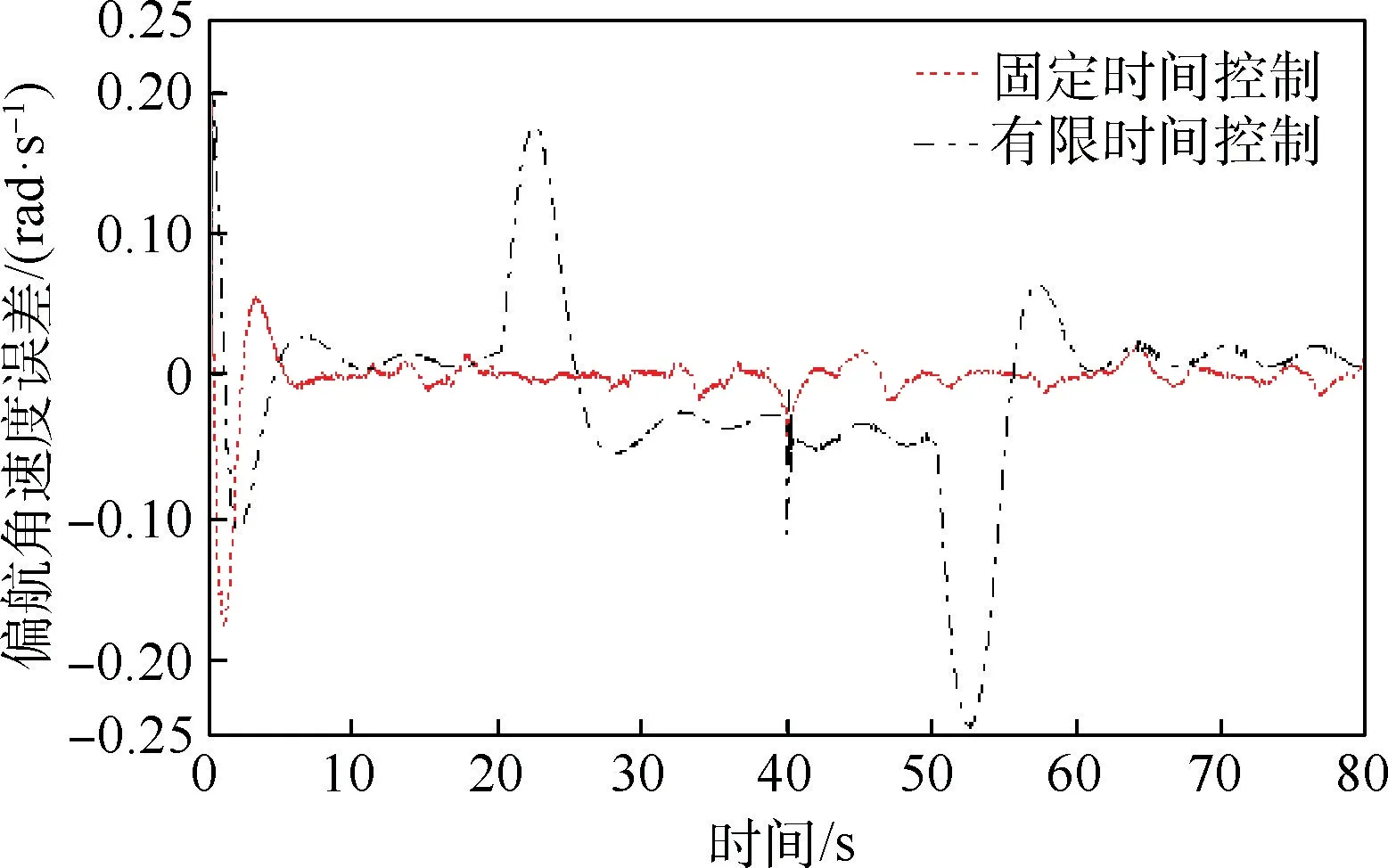
图7 偏航角速度误差Fig.7 Yaw angular velocity errors


为了验证系统初始状态对收敛时间的影响程度,本文选取无人机初始状态2:[x0,y0,e0] =[ -10.6,10.6,15]m 进行仿真分析,仿真结果如图11 和图12 所示。

图8 力矩控制量Fig.8 moment control variable

图9 干扰估计值Fig.9 Estimates of disturbance

图10 不确定性估计值Fig.10 Estimates of uncertainties

图11 不同初值的路径跟踪效果Fig.11 Path following performance with different initial states
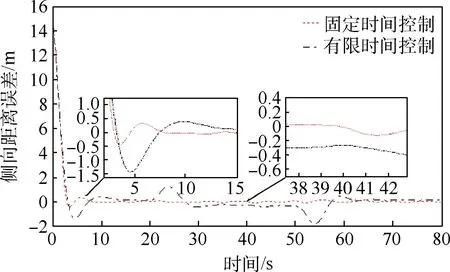
图12 不同初值的侧向距离误差Fig.12 Cross-track errors with different initial states
从图11、图12 可以看出,本文算法在初始状态2 下的收敛时间约为8 s,与状态1 得到的结果相近,受到初始状态变化的影响很小。 有限时间控制算法的收敛时间约为14 s,与状态1 中得到的结果12 s 相比,收敛时间受到初始状态的影响比本文算法更大。 可见本文算法相比有限时间控制算法,初始状态变化对收敛时间的影响更小,能够更加快速精确地跟踪期望路径。 本文算法的绝对误差积分为25。 有限时间控制算法的绝对误差积分为51.75,可见本文算法在新的初始状态下依然具有较高的控制精度。
为了进一步验证初始状态对收敛时间的影响,本文针对初始侧偏进行蒙特卡罗仿真,仿真100 次,每一次初始侧偏在5 ~15 m 上以均匀分布概率随机产生,对所有仿真的侧偏收敛情况进行统计,图13 为所有仿真的收敛时间,表1 列出了收敛时间的统计特性。
从图13 及表1 可以看出,有限时间控制算法的收敛时间受初始侧偏的影响明显,而本文算法的收敛时间更短,并且几乎不受初始状态的影响。 综上所述,本文算法具有更好的快速性和控制精度,系统的收敛时间更短,并且几乎不受初始状态影响,同时对于未知干扰值具有良好的鲁棒性。

表1 100 次仿真统计结果Table 1 Statistic results of 100 simulations

图13 收敛时间统计结果Fig.13 Statistic results of convergence time
4 结 论
1) 本文提出了一种基于扰动观测器的固定时间收敛视线制导控制算法。 通过引入反步法和固定时间控制理论,保证系统具有更快的收敛时间及更好的跟踪精度。 同时结合自然指数障碍李雅普诺夫函数,确保系统状态误差保持在期望的误差限制范围以内。
2) 利用固定时间扰动观测器对时变的执行机构故障和未知环境干扰进行快速精确估计补偿,使控制算法具有较强的鲁棒性和抗干扰能力。
