混沌麻雀搜索优化算法
2021-09-11吕鑫慕晓冬张钧王震
吕鑫 慕晓冬 张钧 王震
(1. 火箭军工程大学 作战保障学院, 西安 710025; 2. 北京遥感设备研究所, 北京 100854;3. 火箭军工程大学 导弹工程学院, 西安 710025)
群体智能优化算法的中心思想是通过模拟自然界中一些事物或生物的运动及行为规律,搜索分布在一定范围内解空间的最优解[1]。 人们通过蚂蚁、蜜蜂、狼、鲸鱼和鸟类等各种生物的群集行为,提出了许多群体智能优化算法,包括蚁群优化(Ant Colony Optimization, ACO)算法、粒子群优化(Particle Swarm Optimization, PSO)算法、人工蜂群优化(Artifical Bee Colony, ABC)算法、灰狼优化(Grey Wolf Optimization, GWO)算法、鲸鱼优化算法(Whale Optimization Algorithm, WOA)、麻雀搜索算法(Sparrow Search Algortihm, SSA)等。 其中,Xue 和Shen[2]于2020 年提出的SSA是一种新型群体智能优化算法。 由于群体智能优化算法具有实现简单、易于扩充和自组织性等优点,受到越来越多研究者的关注。
SSA 相较于其他群体智能优化算法具有搜索精度高、收敛速度快、稳定性好、鲁棒性强等特点。然而,SSA 同其他群体智能优化算法一样,当其搜索接近全局最优时,依旧会出现种群多样性减少,易于陷入局部最优等问题。
为改善群体智能优化算法在接近全局最优时,种群多样性减少,易于陷入局部最优等缺陷,很多学者提出了改进。 刘明霞等[3]将混沌算子引入ACO 算法,提出了一种基于聚度的自适应动态混沌蚁群算法,在增加种群多样性的基础上避免算法陷入局部最优。 杨万里等[4]发现混沌理论可以使PSO 算法的惯性权重具有混沌搜索能力,从而提出一种基于Logistic 映射的新型混沌简化PSO 算法,降低了算法陷入局部最优的能力。董丽凤等[5]针对PSO 算法的早熟问题,通过设定种群多样性阈值,以混沌映射为基础更新当前最优个体位置,并以新方式进行优化操作,在算法的收敛速度和寻优精度上均得到提高。 韩敏和何泳[6]将一种带有高斯函数和混沌特性的变异算子引入PSO 算法,协助种群跳出局部最优,增强全局搜索能力。 文献[7-8]分别将混沌Logistic 映射和Tent 映射用于GWO 算法种群初始化,避免了随机种群的缺点,提高了算法的收敛性。 郝晓弘等[9]提出了一种混合策略改进的WOA 算法,利用Tent 映射初始化种群,为全局搜索奠定基础。 匡芳君等[10]为改善ABC 算法的收敛性能,提出了一种自适应Tent 混沌搜索的人工蜂群算法,避免算法陷入局部最优。
上述文献对群体智能优化算法的改进在一定程度上避免算法陷入局部最优,提高了搜索能力,但仍存在算法搜索精度不足,开拓能力弱等缺陷。考虑到高斯分布较好的局部搜索能力,以及Tent混沌序列遍历均匀、收敛快等特点,提出一种混沌麻雀搜索优化算法(Chaos Sparrow Search Optimization Algorithm, CSSOA)。 该算法首先利用Tent混沌映射初始化种群,使得初始个体尽可能分布均匀,同时引入高斯变异和混沌扰动,当种群出现“聚集”或者“发散”时对个体进行调整,帮助个体跳出局部最优。 本文对12 个基准函数进行仿真实验,并将其应用到简单图像分割问题,验证了本文算法的可行性和有效性。
1 麻雀搜索算法
SSA 是受麻雀觅食行为和反捕食行为启发而提出的一种新型群体智能优化算法,其仿生学原理如下:
麻雀觅食过程可抽象为发现者-加入者模型,并加入侦察预警机制。 发现者本身适应度高,搜索范围广,引导种群搜索和觅食。 加入者为获得更好的适应度,跟随发现者进行觅食。 同时,加入者为提高自身捕食率,部分加入者会监视发现者以便于进行食物争夺或在其周围进行觅食。 而当整个种群面临捕食者的威胁或者意识到危险时,会立即进行反捕食行为。
在SSA 中,模拟麻雀觅食过程获得优化问题的解。 假设在一个D维搜索空间中,存在N只麻雀,则第i只麻雀在D维搜索空间中的位置为Xi=[xil,…,xid,…,xiD],i= 1,2,…,N,xid表 示第i只麻雀在第d维的位置。
发现者一般占到种群的10% ~20%,位置更新公式为
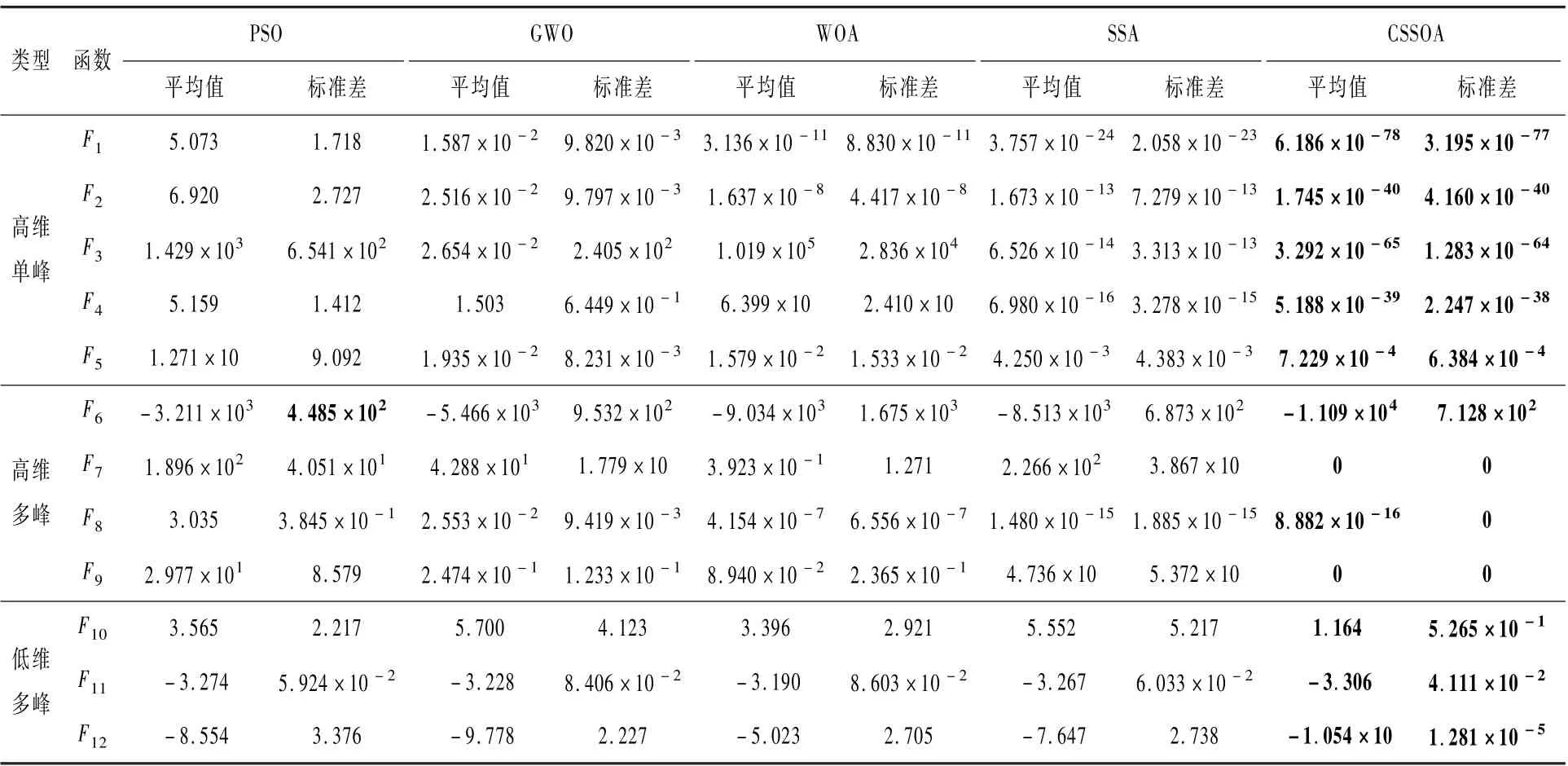
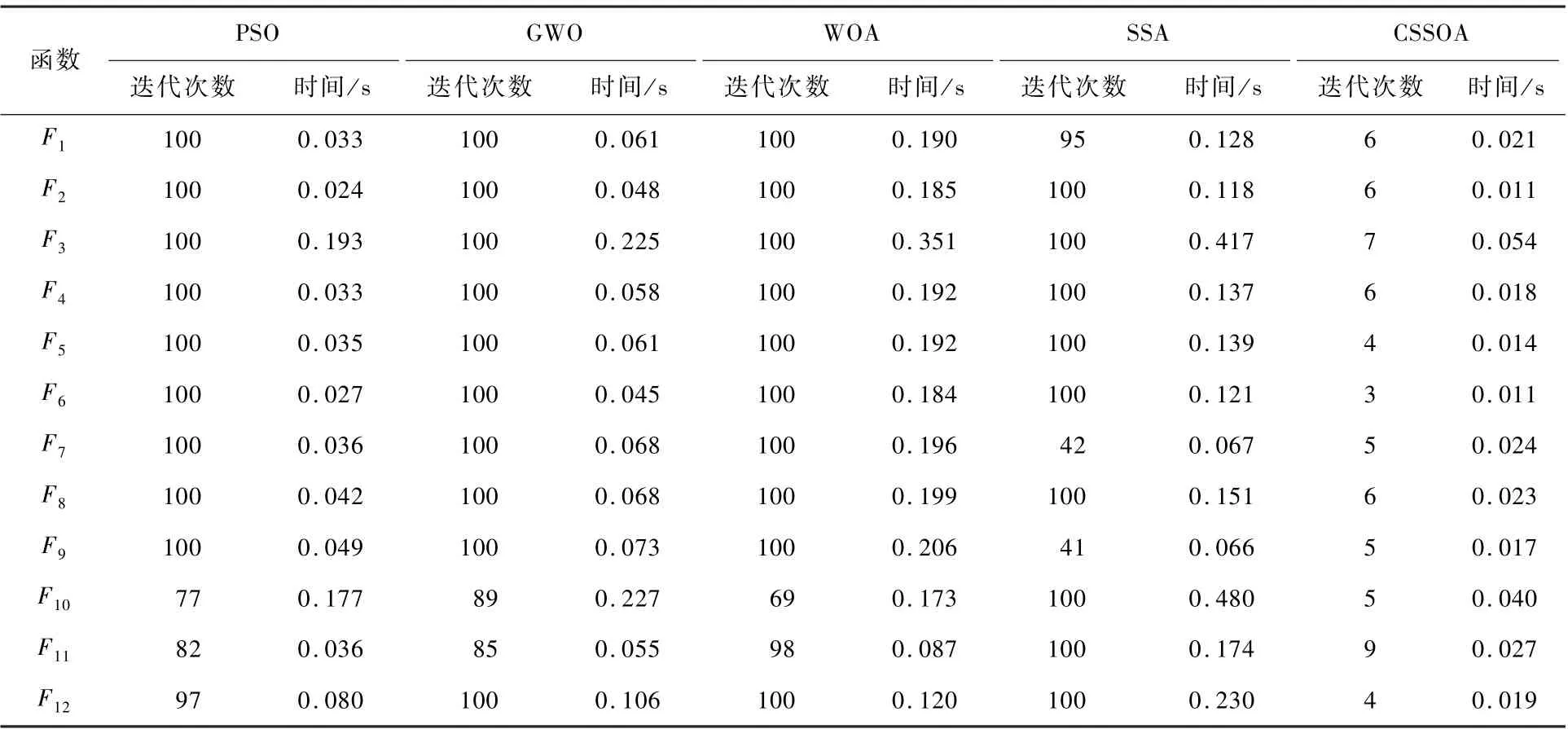
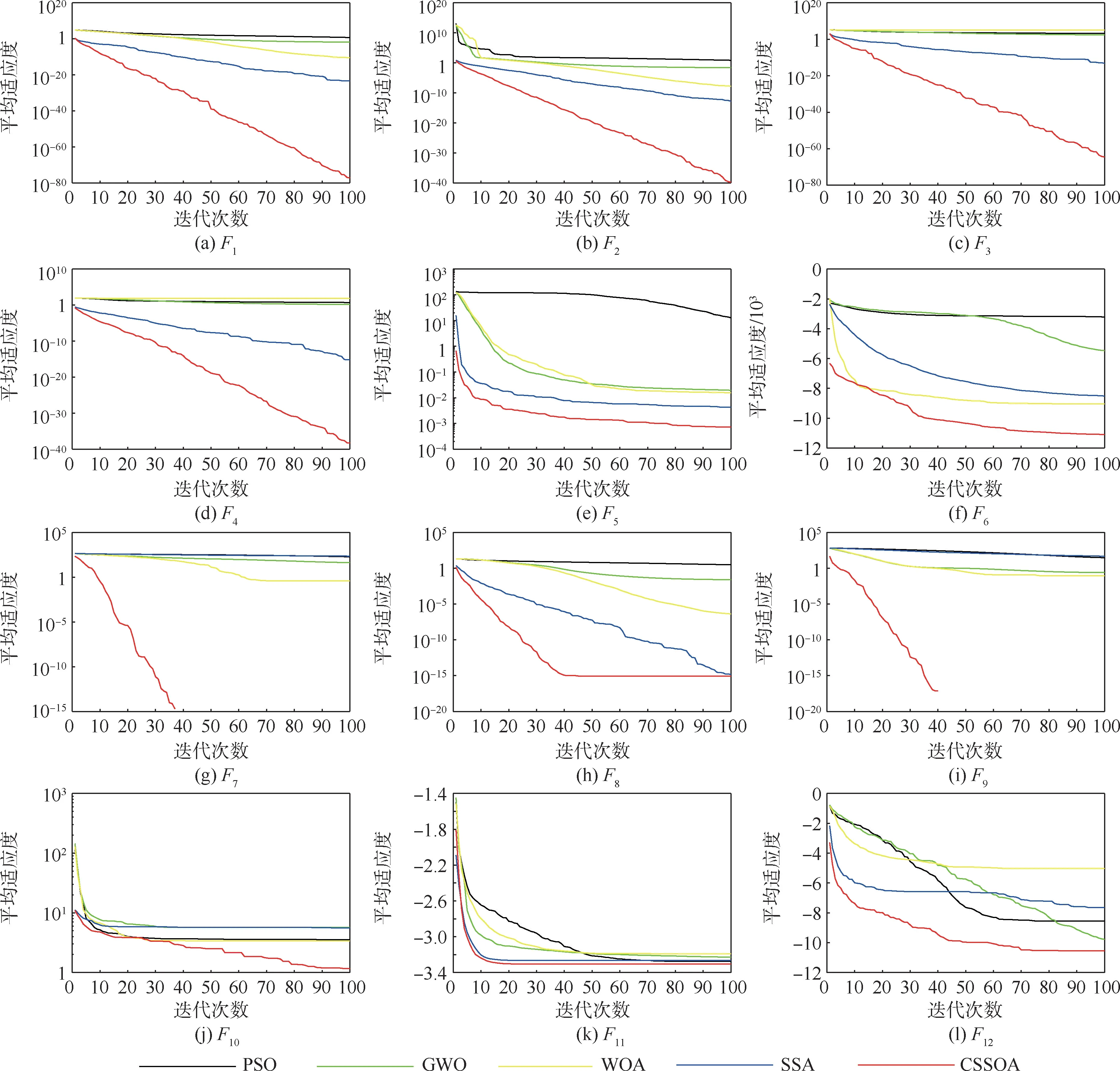
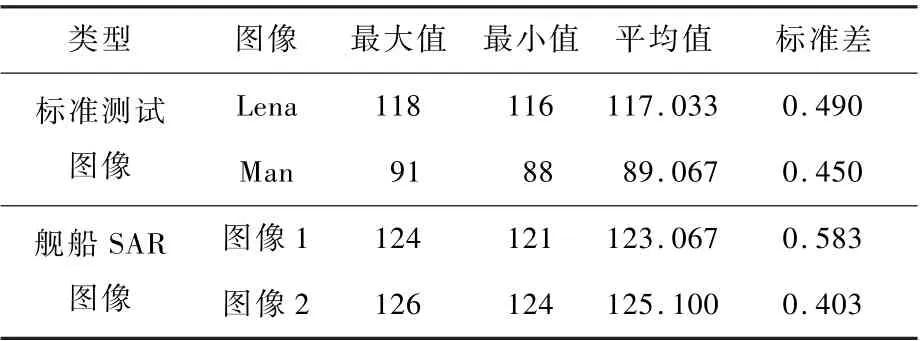
式中:t为当前迭代次数;T为最大的迭代次数;α为(0,1]之间的均匀随机数;Q为服从标准正态分布的随机数;L为大小为1 ×d,元素均为1 的矩阵;R2∈[0,1]和ST∈[0.5,1]分别为预警值和安全值。 当R2 除了发现者,剩余的麻雀均作为加入者,并根据式(2)进行位置更新: 式中:β为步长控制参数,是服从均值为0,方差为1 的正态分布随机数;K为[ -1,1]之间的一个随机数,表示麻雀移动的方向,同时也是步长控制参数;e为一个极小常数,以避免分母为0 的情况出现;fi为第i只麻雀的适应度值;fg和fw分别为当前麻雀种群的最优和最差适应度值。 当fi≠fg时,表明该麻雀正处于种群的边缘,极易受到捕食者攻击;当fi=fg时,表明该麻雀正处于种群中间,由于意识到捕食者的威胁,为避免被捕食者攻击,及时靠近其他麻雀来调整搜索策略。 2.1.1 Tent 混沌序列 混沌作为自然界普遍存在的一种非线性现象,因混沌变量具有随机性、遍历性和规律性的特点[11],被很多学者应用于优化搜索问题,不仅能有效保持种群的多样性,而且有利于算法跳出局部最优,改善全局搜索能力。 常见的Logistic 映射是一种典型的混沌系统,由图1 可以看出,其在[0,0.05]和[0. 9,1]2 个范围的取值概率较高,因此算法寻优速度受Logistic 遍历不均匀性的影响,寻优效率会降低。 单梁等[12]研究表明,Tent映射的遍历均匀性和收敛速度均优于Logistic 映射,并通过严格的数学推理,证明了Tent 映射可以作为产生优化算法的混沌序列。 Tent 映射表达式为 图1 Logistic 混沌序列分布Fig.1 Logistic chaotic sequence distribution 式中:NT为混沌序列内的粒子个数;rand(0,1)为[0,1]之间的随机数。 根据Tent 映射的特性,在可行域中产生混沌序列的步骤如下: 步骤1 随机产生(0,1)内的初值z0,记i=0。 步骤2 利用式(8)进行迭代,产生Z序列,i自增1。 步骤3 如果迭代达到最大次数,程序运行停止,保存产生的Z序列。 2.1.2 Tent 混沌扰动 本文算法引入混沌扰动,避免其陷入局部最优,提高了全局搜索能力和寻优精度。 混沌扰动的步骤描述如下[14]: 步骤1 应用式(8)产生混沌变量Zd。 步骤2 将混沌变量载波到待求解问题的解空间: 式中:dmin和dmax分别为第d维变量Xdnew的最小和最大值。 步骤3 按式(10)对个体进行混沌扰动: 式中:X′为需要进行混沌扰动的个体;Xnew为产生的混沌扰动量;X′new为混沌扰动后的个体。 高斯变异来源于高斯分布,具体指在进行变异操作时,用符合均值为μ,方差为σ2的正态分布的一个随机数来替代原来的参数值[15]。 变异公式为 式中:x为原来的参数值;N(0,1)表示期望为0,标准差为1 的正态分布随机数;mutation(x)为高斯变异后的数值。 由正态分布特性可知,高斯变异的重点搜索区域为原个体附近的某个局部区域。 高斯分布局部搜索能力强,对具有大量局部极小值的优化问题,有利于算法高效、高精度地找到全局极小值点,同时还提高了本文算法的鲁棒性[16]。 CSSOA 算法引入Tent 混沌搜索和高斯变异,增加了种群多样性,提高了算法的搜索性能和开拓性能,避免陷入局部最优,其具体实现步骤如下: 步骤1 初始化,包括种群规模N,发现者个数pNum,侦察预警的麻雀个数sNum,目标函数的维数D,初始值的上下界lb、ub,最大迭代次数T或者求解精度ε。 步骤2 应用2.1.1 节中的Tent 混沌序列初始化种群,生成N个D维向量Zi,并将其各分量通过式(9)载波到原问题空间变量的取值范围内。 步骤3 计算每只麻雀的适应度fi,选出当前最优适应度fg和其所对应的位置xb,以及当前最劣适应度fw和其对应的位置xw。 步骤4 选取适应度优的前pNum个麻雀作为发现者,剩余的作为加入者,并根据式(1) 和式(3)更新发现者和加入者的位置。 步骤5 从麻雀种群中随机选取sNum只麻雀进行侦察预警,并根据式(4)更新其位置。 步骤6 一次迭代完成后,重新计算每只麻雀的适应度值fi和麻雀种群的平均适应度值favg。 1) 当fi 2) 当fi≥favg时,表明出现“发散”趋势,按2.1.2节对个体i进行Tent 混沌扰动,如果扰动后的个体性能更优,则用扰动后的个体替代扰动前的个体,否则保持原个体不变。 步骤7 根据麻雀种群当前的状态,更新整个种群所经历的最优位置xb 和其适应度fg,以及最差位置xw 和其适应度fw。 步骤8 判断算法运行是否达到最大迭代次数或者求解精度,若是,循环结束,输出寻优结果;否则返回步骤4。 为验证CSSOA 的可行性和优越性,对12 个不同类型的基准函数进行仿真实验。 如表1 所示,5 个高维单峰函数F1~F5,4 个高维多峰函数F6~F9,3 个低维多峰函数F10~F12。 通过多种类别基准函数可充分考察CSSOA 的寻优能力。 表1 基准函数Table 1 Benchmark functions 在Intel(R)Core(TM)i5-4300M CPU@2.50 GHz,内 存 4. 00 GB, Windows10 系 统 和 MATLAB R2015a 下对本文算法进行仿真实验,并与PSO、GWO、WOA 和SSA 算法进行对比。 实验中取种群规模N=30,最大迭代次数T=100,目标函数的维数D和初始值的上下界ub 和lb 按照表1 中各基准函数具体选定,发现者个数pNum和侦察预警的麻雀个数sNum均取种群规模的20%。 为避免寻优结果的偶然性,以及证明CSSOA 的稳定性,选取各基准函数独立运行30 次的实验结果作为实验数据。 针对12 个基准函数,将各个算法的平均值和标准差作为最终评价指标,如表2 所示,表中数据加粗表示各函数各指标最优值。 表2 基准函数优化结果比较Table 2 Optimization result comparison of benchmark functions 表2 的实验结果表明,对于高维单峰函数F1~F4,CSSOA 无论是在寻优稳定性还是寻优精度上都比其他4 种算法有极大的提升,且CSSOA多次寻优的平均值和标准差相较于其他4 种算法均提升了23 个数量级以上;而对于函数F5,虽然CSSOA 的寻优性能提升不明显,但寻优结果和稳定性仍优于其他4 种算法。 对于高维多峰函数F7和函数F9,CSSOA 均能有效跳出局部最优,稳定找到全局最优解,鲁棒性强;对于函数F6,CSSOA 寻优性能提升不明显;对于函数F8,CSSOA寻优性能提升不大,但其多次寻优的标准差为0,因此具有较强的稳定性。 对于低维函数F10~F12,虽然CSSOA 多次寻优的平均值和标准差相较于其他4 种算法提升不高,但是CSSOA 的寻优精度较高,且由CSSOA 多次寻优的标准差可以看出,CSSOA 寻优的稳定性均明显优于其他4 种算法。 实时性作为评价算法的重要指标,表3 给出了各算法在30 次独立运行下的平均迭代次数和平均运行时间。 分别将表2 中函数F1~F12的标准差量级作为算法求解精度ε(F6取0.001),当算法寻优过程中前后2 次结果差值的量级小于ε时终止迭代。 以函数F1为例,从表3 可以看出,CSSOA 的平均迭代次数较PSO、GWO 和WOA 均减少了94.00%,较SSA 减少了93.68%,平均运行时间较PSO、GWO、WOA 和SSA 分别提高了36.51%、65. 81%、89. 04%、82. 74%,故CSSOA寻优过程的实时性表现良好。 表3 基准函数的优化结果比较Table 3 Optimization result comparison of benchmark functions 为了反映CSSOA 的动态收敛特性,图2 给出了12 个基准函数在5 种优化算法下的收敛曲线。对于函数F1、F2、F3、F4、F7、F9,CSSOA 在收敛速度和寻优精度上都明显优于其他4 种算法,且迭代前期的搜索性能和迭代末期的开拓性能也都优于其他4 种算法,表明CSSOA 在保证开拓能力的同时也能充分保证搜索能力,不失种群多样性和寻优稳定性。 对于函数F5、F10、F12,CSSOA 的收敛速度也均优于其他4 种算法,虽然在末期有陷入局部最优的趋势,但是由于引入了高斯变异和Tent 混沌扰动,种群能够有效地跳出局部最优,得到较好的寻优精度。 对于函数F6,多次寻优的标准差高于PSO 和SSA,稳定性略差,但从平均值可以看出,SSA 可有效收敛到全局最优解,而其他4 种算法则容易陷入局部最优。 对于函数F8,CSSOA 和SSA 收敛结果相近,但可以看出CSSOA收敛速度明显比SSA 快。 对于函数F11,5 种算法最终都趋于平稳,但CSSOA 在寻优精度上仍优于其他4 种算法。 图2 5 种算法在基准函数上的收敛曲线比较Fig.2 Comparison of convergence curves of 5 algorithms obtained on benchmark functions 综上所述,CSSOA 对12 个基准测试函数的寻优性能提升明显,且稳定性好、鲁棒性强,特别是函数F1~F4,CSSOA 的寻优性能相较其他4 种算法高出20 个数量级,优势明显;同时,CSSOA的收敛速度明显优于其他4 种算法,且实时性表现良好,能够有效避免陷入局部最优,寻优精度高、搜索能力强,由此证明了CSSOA 的可行性和优越性。 本节采用实际工程中常见的图像分割问题对CSSOA 应用于实际工程问题的可行性进行检验。 大津法(Otsu)作为一种图像二值化处理的高效算法,指的是将原图像分为前景图像和背景图像,并将类间方差作为衡量分割阈值的标准,使得类间方差最大的分割阈值即为最佳阈值。 本节采取类间方差作为CSSOA 的适应度函数,数学表达式为 fitness=w0w1(μ0-μ1)2(12) 式中:w0为前景像素占整幅图像的比例;μ0为其平均灰度;w1为背景像素占整幅图像的比例;μ1为其平均灰度。 CSSOA 进行图像阈值分割,即找到一个最优解(麻雀位置),使得适应度函数取得最大值,并利用该解对图像进行二值分割。 初始化种群规模N=20,最大迭代次数T=100,目标函数的维数D=1,初始值的上界ub =255,下界lb =0,对2 幅标准测试图像和SSDD 数据集[17]中的2 幅舰船SAR 图像分别进行30 次阈值分割,得到分割阈值的最大值、最小值、平均值和标准差,如表4 所示。 通过枚举法求得4 幅图像的最佳一维Otsu阈值依次是117、89、123 和124,然后将CSSOA 与Otsu 的分割结果进行比较,如图3、图4 所示。 表4 数据表明,CSSOA 图像分割阈值稳定分布在最佳一维Otsu 阈值周围,收敛效果明显。 由图3和图4 可以直观看出,CSSOA 可以得到和Otsu相似的分割结果。 由此验证了CSSOA 应用到实际工程问题的可行性,为下一步研究奠定了基础。 表4 图像分割阈值Table 4 Image segmentation threshold 图3 标准测试图像分割结果Fig.3 Segmentation results of standard test image 图4 舰船SAR 图像分割结果Fig.4 Segmentation results of ship SAR image 1) CSSOA 寻优性能提升明显。 例如CSSOA在12 个基准测试函数的寻优结果均优于其他4种优化算法,且对部分函数的性能提升达到20 个数量级以上。 2) CSSOA 寻优精度高,具有优良的开拓能力。 引入高斯变异和Tent 混沌扰动,丰富了种群多样性,避免CSSOA 陷入局部最优,增强了算法的全局搜索能力。 3) CSSOA 具有良好的稳定性,鲁棒性强。CSSOA在12 个基准测试函数上多次寻优的标准差普遍低于其他4 种算法的标准差,且在1 个数量级以上,寻优结果稳定。 4) CSSOA 收敛速度快、搜索能力强,且表现出良好的实时性。 从CSSOA 的收敛曲线直观看出其收敛速度明显优于其他4 种算法,同时平均迭代次数和平均运行时间也反映了CSSOA 较其他传统算法更优异的实时性表现。 CSSOA 的研究还在初始阶段,后续考虑将其应用到实际工程问题中,如图像分割、旅行商问题、人脸识别等,并结合具体问题进一步优化算法性能,检验CSSOA 在实际工程问题中的有效性。
2 Tent 混沌及高斯变异
2.1 Tent 混沌


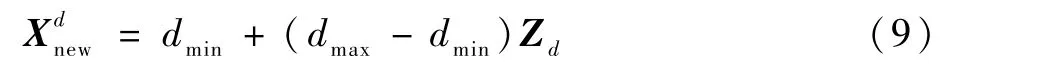

2.2 高斯变异

3 改进麻雀搜索算法
4 仿真实验与结果分析
4.1 实验设计与基准函数

4.2 算法性能对比分析
5 CSSOA 在工程问题中的应用


6 结 论
