手工制作融入数学教育教学的探究

朱旭颖

摘 要：用数学教学实践案例说明手工制作融入数学教育教学的可行性，落实用数学眼光观察世界的数学教育理念，一方面把抽象的数学概念渗透于劳动教育之中，另一方面在劳动中提升数学教育的质量，养育中学生的核心素养与思维品质。

关键词：劳动教育;数学教学;核心素养;教育功能

手工制作是一种劳动的一种形式，劳动是人维持自我生存和自我发展的唯一手段.劳动可分为脑力劳动和体力劳动。劳动教育是使学生树立正确的劳动观点和劳动态度，热爱劳动和劳动人民，养成劳动习惯的教育，能直接决定着学生的劳动精神面貌、劳动价值取向和劳动技能水平。2020年新高考数学命题中开始渗透劳动教育的命题，劳动教育重在“育”，重在渗透。作者在多年的教学实践中，积极探索劳动教育如何渗透数学教学，现将实践具体案例与探究思考呈现，以引起教师关注。

一、动手制作成习惯

（一）落实用数学眼光看世界理念

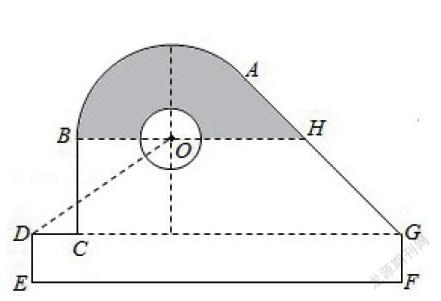
2020年修改版《普通高中数学课程标准》已将“用数学眼光观察世界”作为数学教育的基本理念写入课程标准[1]，将数学“劳动实习”引入高考，其教育功能显而易见.关键是教师要有落实这一理念的自觉行动.2020年新高考山东数学命题就是最好的例证。“某中学开展劳动实习，学生加工制作零件，零件的界面如图所示，O为圆孔及轮廓圆弧AB所成圆的圆心，A是圆弧AB与直线AG的切点，B是圆弧AB与直线BC的切点，四边形DEFG为矩形，BCDG，垂足为C，，BH∥DG，EF=12cm，DE=2cm，A到直线DE和EF的距离均为7cm，圆孔半径为1cm，则图中阴影部分面积为____cm2”

（二）养成数学眼光观察环境习惯

2020年某日在辅导新高三学生时，遇到一件尴尬的事，请学生做下列三视图题：

（2020年浙江卷第5题）某几何体的三视图如图所示，则该几何体的体积是（   ）

此学生对此三视图的直观图脑海中没有印象，画不出其直观图。然而，此学生的眼镜盒就放在桌前如照片，此问题情境贴近此题直观模型，为什么学生天天用的眼镜盒（几何体）没有在自己的脑海中形成数学概念呢？事实上，学生缺少“用数学眼光观察周围事物”的意识，也说明现实的数学教学脱离实际.当给学生以眼镜盒为模型解读后学生顿悟。事实上，在教学中学会用身边的物件解读数学概念与方法，引导学生学会用数学眼光观察是非常重要的。

（三）培养动手制作小物品的习惯

在立体几何教学中引导学生制作空间图形是“劳动教育”最佳载体.比如“玩泥巴”——用泥土制作三棱锥、四棱锥、正方体等，用刀切割上述几何体观察截面形状培养空间概念;再如，“搭建几何体”——用羊肉串签搭建正四面体、正方体等。教学中遇到一非常好的案例：一个正方体铁丝框架，在8个顶点处焊接小钩子，每个面的面对角线由橡皮筋挂在小钩子上，学生用两只手拿着一对橡皮筋在“玩”，并将一对面对角线橡皮筋向外拉，当一位、二位、三位学生参与此活动后，提出并判断下列前3个问题的正确性，探究第4个问题的规律：

（1）一个成员抓住一对面的面中心向外拉成十二面体;

（2）二个成员同时抓住两对面的面中心向外拉（垂直面的距离相同）成十八面体;

（3）三个成员同时抓住三对面的面中心向外拉（垂直面的距离相同）成二十四面体;

（4）在上述动手实验过程中构造了许多多面体，请研究一下，这些多面体的棱数、面数、顶点数之间有没有规律？

学生发现第（1）个正确，第（2）（3）个必须有限制条件才能成立，学生在“玩”中不仅理解了凸多面体的概念，在第（4）问题中还发现了“欧拉公式”。

二、实验实习成风气

（一）用数学方法参与动手实验

解三角形教学后组织学生测量建筑物高度就是一个动手实验的过程，在2017年版2020年修改《普通高中数学课程标准》的案例15与2000年第2期《中学数学教学》 “ 培养中学生数学创造性思维的途径”文章中都有介绍[2].

（二）用亲自调查参与社会实习

针对学习生活中某些问题，设计一个项目进行调查研究，用数学的方法解决，这期间可以进行数学“建模”实习，由于需要动手参与才能完成.比如，在2010年第12期《数学通报》“新课程数学中实习作业的教育价值与设计——实习作业型设计”文章中介绍的课桌椅的设计问题[3]，就是组织学生参与数学实习，动手测量，设计方案，建立数学模型，提出解决问题的建议，在此过程中离不开劳动体验.

（三）数学实验探究中体验劳动

爬（上）楼梯已成为年轻人锻炼身体，体验劳动的一种方式，然而在爬（上）楼梯的过程中，可以设计数学实验活动.按身材高低分成两个小组，一个小组A身材较矮腿较短，一步只能上一阶或二阶楼梯;另一小组B身材较高腿较长，一步能上一阶或二阶或三阶楼梯，分别思考上1，2，3，4，…，10阶楼梯的方法数.有人亲自爬（上）楼梯，有人在旁边计算方法数，对于高一的学生可以开展此项活动，会有各种意想不到的结果.当然，一旦接触数列知识后，特别是了解“斐波那契数列”递推方法后，他会觉得他的劳动是值得的，特别是B组的学生，能够寻找到方法数的一般模型（通项公式）吗？

三、动脑思考成品质

教学中渗透的“劳动”观念，更多的是动手与动脑的结合，特别是动手实践中要多“思”，养成从不同的视角去思考问题的品质.

（一）手工制作劳动中数学思考

2020年新高考山东卷第15题“加工制作零件”，正是引导学生数学逻辑推理中学会综合应用.比如下列问题是一个经典的手工制作劳动：

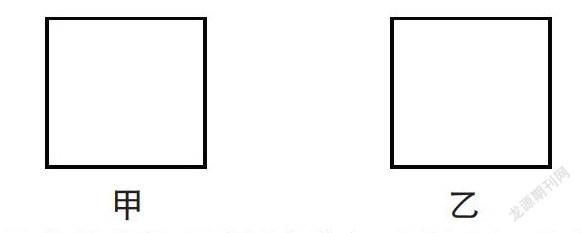
婚礼上需要大量的喜糖，某包装公司为包装喜糖设计两种包装盒，如图，甲、乙是边长为4a的两块正方形硬紙板，现将甲剪接成一个正四棱柱型包装盒，将乙裁剪接成一个正四棱锥型包装盒，使它们的全面积都等于原正方形的面积（不计粘贴缝的面积）（Ⅰ）将你的裁剪方法用虚线标示在图中，并作简要说明;（Ⅱ）试比较你所制作的正四棱柱包装盒与正四棱锥包装盒体积的大小，并证明你的结论。

以上裁剪方法有很多种（略），进一步数学思考拓展：

探源（1）将一个正方形分割拼接成一个正四棱柱，正方形的面积为16a2，拼接的正四棱柱的表面积2b2+4bh也为16a2，从理论上说b、h的选择方法有无数种，只是人们会从较易拼接的角度去思考，因b2+2bh=8a2，即b（b+2h）=a×8a= 2a×4a=a×4a=…，从而选择b=a，h=3.5a;b=2a，h=a;b=a，h=1.5a;…，但仍要考虑可拼性，否则会犯错误。

（2）将一个正方形分割拼接成一个正四棱锥，正方形的面积为16a2，拼接的正四棱锥的表面积b2+4×bh′也为16a2，同样b、h′的选择方法也有无数种，人们也会从较易拼接的角度去思考，因b2+2bh′=16a2，即b（b+2h′）=2a×8a=4a×4a=2 a×8a=…，从而选择b=2a，h′=3a;b=4a，h′=0（一种不可拼的情形）;b=2a，h′=3a;…深化（1）对于给定的正方形，裁剪成的正四棱柱的体积V柱=4a3是最大值吗？

数学直觉告诉我们，对于给定的正方形，只要所剪接的正四棱柱接近于正方体，则体积可以达到最大。设正四棱柱底面边长为b，高为h，则问题转化为求V=b2h在条件b2+2bh=8a2下的极值问题，

当且仅当b=h=a时，取等号，即所剪拼的正四棱柱为正方体时，体积最大，最大体积为a3（2）对于给定的正方形，裁剪成的正四棱锥的体积V锥=a3是最大值吗？

设正四棱锥的底面边长为b，高为h，斜高为h′，则问题转化为：求V=b2h在条件b2+2bh′=16a2，h′2=h2+（）2下的极值问题。

（二）劳动实践中学会数学思考

社会实践——游学正成为学生一种特别的学习方式。比如在瑞士登（爬）雪郎峰时，乘坐四段缆车的过程可以数学思考，把函数融合在旅游之中。乘缆车登雪山可设计分段函数，海拔高度与起点水平距离之间关系，给出缆车速度，研究乘坐缆车登山时间，提出下列数学思考：

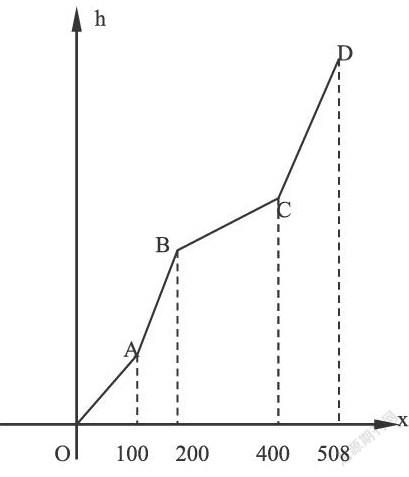
问题：在瑞士登雪郎峰时要乘坐四段缆车才能到达海拔2970m的峰顶，海拔高度 （m）与起点水平距离 （m）之间关系图象如图，起点O（0，0），A（100，500），B（200，1300），C（400，2100），D（508，2964），

（Ⅰ）写出函数h（x）的表达式;

（Ⅱ）如果缆车的行驶速度为6公里/小时，且中间需要三次换乘打卡，每次用时2分钟，则游客从山底到山顶乘缆车需要多少分钟？

（三）动手与动脑相结合育品质

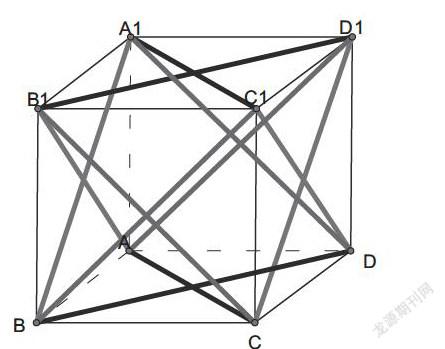
劳动教育与数学教育的融合最明显的特征是动手与动脑结合，直观与抽象结合，创新与创造结合，比如，下列动手实验类似于上述正方体的动手“玩”：一个单位正四面体框架（铁丝），四个面为中软橡皮，玩一个数学游戏，抓住各面的面中心向外拉且垂直相应的面，拉的长度（垂直面的距离）设为d，构造新的凸多面体，试判断下列结论是否正确？

（Ⅰ）一位学生抓住一个面的面中心向外拉，构成七面体;

（Ⅱ）二位学生同时抓住二个面的面中心向外拉，構成十面体;

（Ⅲ）三位学生同时抓住三个面的面中心向外拉，构成十三面体

（Ⅳ）四位学生同时抓住四个面的面中心向外拉，构成十六面体

事实上，作为一个劳动者，每时每刻的劳动都离不开动手与动脑，在数学教学中把它们有机结合对学生而言是一件非常愉快的事，对教育者而言，正是在养育学生的劳动品质。

参考文献

[1]普通高中数学课程标准[M]，中华人民共和国教育部制定，2017年版2020年修订，48-50

[2]余继光，培养中学生数学创造性思维的途径[J]，中学数学教学，2000（2）：25-26

[3]余继光，新课程数学中实习作业的教育价值与设计——实习作业型设计[J]，数学通报，2010（12）：23-27