整体规划 分步实施

陈中峰

摘  要：通过对课例“函数应用：停车距离问题”的赏析，阐述对中学数学建模活动的认识与看法，并就数学建模活动中“数学模型优劣的评判问题”及数学教学中学生“数学建模素养的培育问题”提出建议.

关键词：数学建模活动;数学建模素养;数学模型评判

数学建模活动是基于数学思维运用模型解决实际问题的一类综合实践活动，是对现实问题进行数学抽象并用数学语言加以表达、用数学方法构建模型解决问题的过程，包括在实际情境中从数学的视角发现问题、提出问题，并用数学的方法分析问题、构建模型，确定参数、计算求解，检验结果、改进模型，最终解决实际问题. 数学建模活动是落实育人方式改革的重要载体，根据《普通高中数学课程标准（2017年版）》（以下简称《标准》）的要求，数学建模活动要让学生经历完整的解决问题的过程，培养学生数学建模素、数学运算、数学抽象等素养. 因此，整个数学建模活动不可能在一节课中完整展示. 为此，组委会规定本节课可以重点展示开题报告活动和结题交流活动.

“停车距离问题”数学建模活动课，严格按照组委会的相关要求，以“停车距离问题”为例，采用课题研究成果汇报的形式，让学生结合之前所学的函数，借助信息技术手段，根据现实背景和给定的数据（数据来源于《标准》第118页表1），分析其中的变量、常量及相互关系，明确变化的特征，构建急刹车的停车距离数学模型，再通过运算求解函数模型，利用函数模型的解说明实际问题的变化规律，实现解决问题的目的. 在这个过程中，师生共同经历发现问题、收集数据、建立模型、计算求解、检验模型、解决问题等环节，展示了中学数学建模的完整过程，引导学生用数学眼光观察世界，用数学语言表达世界，用数学思维思考世界，积累了解决实际问题的基本活动经验.

一、本节课的优点分析

1. 合理展示，突出建模过程

本节课立足于数学活动课上进行的关于“停车距离问题”课题研究的开题报告及小组交流活动，让三个小组的代表汇报各自的建模过程与成果，分别展示了模型假设、模型建立、模型计算、模型验证和模型改进，获得了解决问题的函数模型，较好地展示了数学建模的全过程. 学生的参与积极性高，过程规范、汇报流畅、条理清晰，反映了执教教师在日常教学中对学生建模思想培养的重视程度.

在学生互评环节中，执教教师组织学生以小组形式展开讨论，对三种建模结果进行评价，分别从过程，结果，验证误差，模型优、缺点等方面进行对比，反映了学生对数学建模的掌握程度及对数学相关知识的理解水平，深化了对建模过程思维严谨性的认识.

2. 科学引导，深化建模认识

课堂上，执教教师对学生进行适时的科学引导，逐步深化学生对建模的认识. 例如，在展示中提出“还有其他不同的数学模型吗”，在评价中提出“已有的三种模型的优、缺点分别是什么”，在总结中提出“回想整节课，你有哪些收获”. 以问题为导向，科学引导学生既完善了对数学建模活动的认知，又深化了对数学建模过程、法律意识及数学运用等方面的了解，并引出了后续研究数学模型的基本方向.

3. 关注应用，揭示建模意义

本节课执教教师结合交通法规的教学，向学生渗透法律意识、安全意识教育，在课堂中融入社会主义核心价值观教育，培养学生的法律意识. 课堂上，执教教师分别引用了《中华人民共和国道路交通安全法实施条例》和《中华人民共和国道路交通安全法》中对机动车设置警告标志距离及高速公路行车间距的规定，引导学生思考法律、法规中数据设置的依据，同学生一起挖掘发现模型的现实应用价值，让学生体会法律、法规中数据的科学性，实现本节课内在的育人目标. 同时，在运用模型解决实际问题的过程中，也揭示了数学建模的现实意义.

此外，在各小组汇报中，还可以感受到各小组在研究过程中都能够娴熟地应用信息技术，特别是对Excel软件的应用. 尤其是小组2，能借助Excel软件模拟函数、修正函数模型. 信息技术的应用既提高了学生的实际操作能力，又为数学建模活动的有效性提供了保障，信息技術的应用与展示也成为本节课的又一亮点.

总之，本节课是一节成功的数学建模示范课，为数学建模进入课堂教学提供了一个可供参照的数学案例，起到了较好的引领示范作用.

二、关于数学建模与数学探究活动的进一步思考

数学建模与数学探究活动作为高中教学的四大主线之一，是新一轮课程改革的一个亮点. 对多数高中数学教师而言是一个新的话题，还是有许多问题值得我们进一步思考.

1. 关于模型优劣的评判问题

许多数学模型的建立，是借助对数据的分析、拟合得到的，特别是函数模型，往往是通过做出散点图，分析散点图的走势，选择函数进行拟合，从而得到函数模型. 那么，应该如何判断这个模型的优劣呢？是不是它与这些测量数据越吻合，拟合度越高，这个模型就越好？从理论上讲，对于函数模型问题，无论有多少组数据，我们总能利用牛顿插值公式，得到一个与这些数据完全“吻合”的函数. 那么这个模型是不是就是最优的模型呢？显然不是. 因为数据的获得是通过测量得到的，而测量往往存在误差. 因此，“吻合度”仅仅是评判一个模型优劣的因素之一. 就本课题而言，由物理学知识可知，在刹车过程中“d”是“t”的二次函数，因此无论其他函数与这些数据的“吻合度”多高，二次函数模型才是本课题的最优模型. 评判一个模型的优劣，应该看这个模型是否能客观地反映所要解决的问题的本质. 例如，用二次函数、三次函数刻画“茶水最佳饮用时间”问题，无论它与测量的数据如何吻合，它们都不是适合的模型，也是这个道理.

2. 关于学生数学建模素养的培育问题

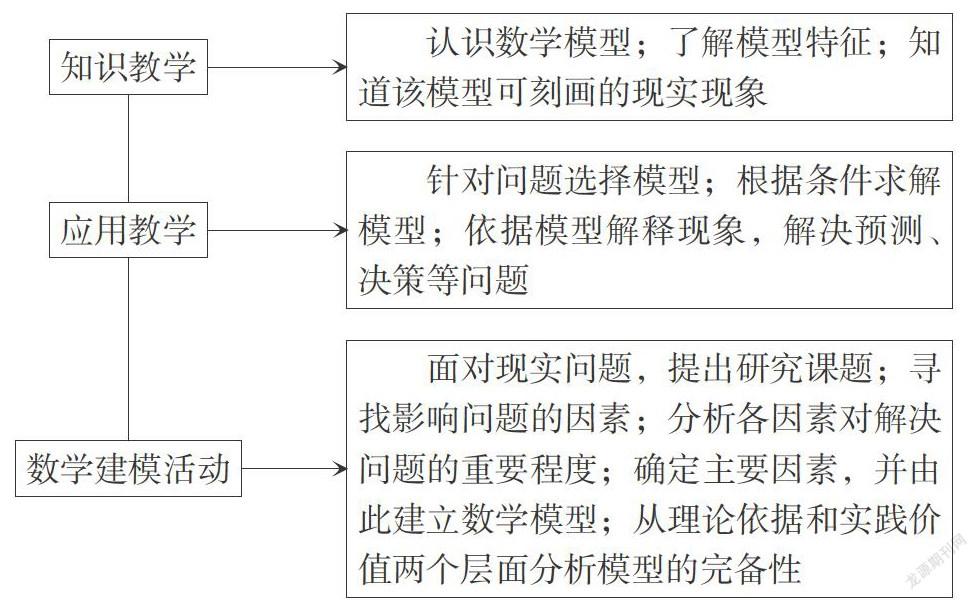
数学建模活动是利用数学知识和方法解决实际问题的应用性实践，是学生数学建模素养的展示. 从课型的角度来讲，它属于“习作课”的范畴，仅仅是促进学生数学建模素养发展的一个环节，而不是全部. 事实上，数学建模素养的培育应贯穿数学教学的全过程，只是在不同的教学阶段，其侧重点也有所不同罢了，具体可用下图表示.

对新课程的知识教学，要让学生在理解这些知识的基础上，根据这些知识的特点，明白这些知识反映的数学模型，明确模型的特征，知道模型可用于刻画哪种现象. 例如，指数函数的教学不但要教给学生相关的知识，而且要让学生理解指数函数模型的变化特点，明白指数函数可用于刻画哪种类型的变化问题. 在习题课的知识应用教学中，要着重教授学生针对具体问题的特点，选择合适的数学模型加以刻画，并会根据问题给出的初始条件求解模型，根据模型解释现象，解决预测、决策等问题. 在数学建模活动中，学生要着重解决面对现实问题如何提出切合实际的有价值的研究课题，并根据研究问题的需要寻找影响问题的因素，对问题进行理想化处理，然后根据这些主要因素建立数学模型，并从实践和理论两个层面分析所建立的模型的完备性，进一步优化模型.

参考文献：

[1]中华人民共和国教育部制定. 普通高中数学课程标准（2017年版）[M]. 北京：人民教育出版社，2018.