高中数学习题课的教学活动的实践探索

张雪峰 李萌

摘 要：中学数学复习是高中数学教学的重要环节，在集体备课活动中要敢于探索，敢于实践，根据学生的学习实际安排合适的复习内容

和学习方法，让学生根据自己的学习实际去组织学习和练习.

关键词：数学复习;集体备课;时间探索

中图分类号：G632文献标识码：A文章编号：1008-0333（2021）15-0004-02

高中数学复习课的教学是高中数学教学的重要内容和环节，在教学中，可以发挥集体的智慧去提高教学效果，特别是在高中数学复习中.组织和安排好集体教学实践活动可以提高教学的效果.

一、精心安排好习题课的教学

“问题是数学的心脏”，习题教学是高中数学课堂教学的重要环节，怎样进行习题课教学？怎样真正培养学生分析问题、解决问题的能力？怎样把习题课教学功能切实发挥出来？这些都是数学教师一直思考的问题，优选恰当的例题，进行适度的变式，采用多样的教学手段，让习题教学功能发挥到最大.

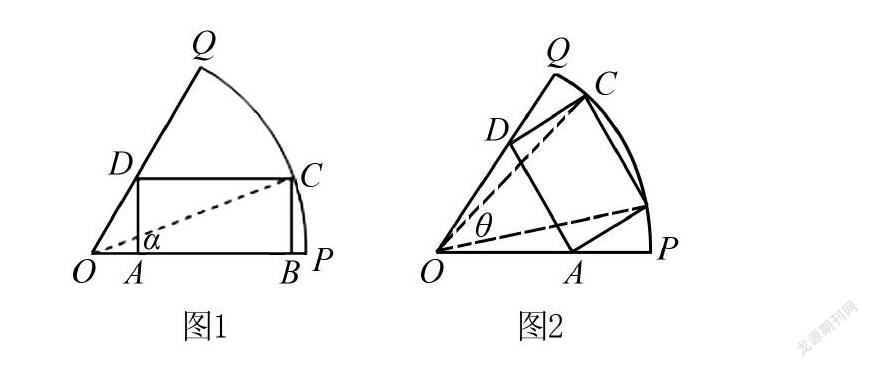
例1 （问题信息源）如图1，已知扇形OPQ是半径为1，圆心角为π3的扇形，C是扇形弧上的动点，ABCD是扇形内接矩形.记∠COP=α，求当角α取何值时，矩形ABCD的面积最大？并求出这个最大面积.这是课本上一道例题，集体备课时，教师们集思广益，改变视角设计变式题：

变式1 已知扇形OPQ是半径为R，圆心角为π3的扇形.如图1，C是扇形弧上的点，ABCD是扇形的内接矩形.记∠COP=α，矩形ABCD的面积记为S（α），求S（α）的最大值.

变式2 如图2，C，B是扇形弧上的两动点（PBEuclid ExtrazB@=QCEuclid ExtrazB@），ABCD是扇形的内接矩形.记∠COB=θ，矩形ABCD的面积记为T（θ），求T（θ）的最大值.

变式3 要想在一块圆心角为θ（0<θ<π），半径为R的扇形铁板中截出一块面积最大的矩形ABCD，应怎样截取？并求出此时的矩形面积.

学生在解题过程中遇到的困难主要表现在：（1）理解困难，对题意不理解或是不易发现隐含条件;（2）构造困难，不会将题中的条件转化为数学信息，列出相应的数学表达式;（3）运算困难，速度慢而且准确率低，常常出现半途而废的现象;（4）判断困难，对概念理解不清，解题结果不会检验.究其原因，学生没有掌握题目本质，很多学生是“记题型，背套路”.所以，充分发挥集体智慧，挖掘题目内涵，以题目为载体构建知识体系，锻炼学生的数学理解能力和数学思维能力，真正学以致用.

二、数学复习课的备课实践

复习课是数学教学中必不可少的一种课型， 数学复习课不同于新授课，它是站在“整体”的高度上，对所学的某章或某节内容的概念、方法、思想的再理解和再提高，是学生综合能力的再提升的过程.在实际教学中，数学复习课存在课堂形式單一，教学效果不明显等问题.数学复习课常常出现两种偏向：一种是以题海代复习，学生听得晕头转向;另一种是整理干巴巴的知识点，学生听得枯燥乏味.因此集体备课时，需要在复习课的准度、深度和难度的定位上下足功夫，提高复习课的教学效率.

1.研究学情，定位复习的“准度”

数学复习课教学的第一步是要研究学情，弄清楚学生在学习一个阶段之后，存在什么样的问题，清楚问题所在，才能有针对性地进行复习，才能恰当地切入复习点，起到复习课应有的作用和功能.

笔者所在的高三数学理科备课组，在进行“函数与导数”专题复习时，把学生平时遇到的问题一一归纳：

（1）函数与导数含了太多的知识点，导数的概念及几何意义、函数与不等式方程的基础知识、导数研究函数的性质等，对学生来说，这些知识在脑子里是杂乱无章的，所以复习的第一步是整理知识点，将它们归纳梳理，形成系统的知识网络;（2）用导数求解切线问题，学生总是将“曲线在某点处的切线”与“曲线过某点的切线”混淆;

（3）用导数研究函数的单调性以及函数的最值问题，这是学生必须掌握的，但碰到含参数的函数，学生还是会频频出错;（4）明确函数的极值与导数对应的方程f ′（x）=0的根之间的关系，即f ′（x0）=0是x0为极值点的必要而不充分条件，这一步骤的检验常被学生忽略，导致结果错误;

（5）学生的分类讨论有待加强;数形结合的意识和能力需大力培养;运算能力要高度重视.

2.钻研考纲，定位复习的“深度”

备课中，教师们要结合考纲，注重落实学生的基础知识，还要清晰地把握重要知识的再现，一方面确定复习课的主线，一方面明确复习的深度.

在“函数与导数”专题复习中，通过集体商议，把这个专题细化为四个小专题：（1）导数的几何意义与切线问题（曲线在某一点处的切线问题）;（2）用导数研究函数性质的问题;（3）不等式恒成立问题（分离参数将其转化为函数的最值问题）;（4）导数的实际应用问题.根据这四个小专题，将复习课的题型总结为：求切线方程、用导数研究函数的单调性（着重是含参数的函数）、用导数求函数的极值与最值、用导数研究不等式、用导数研究方程、导数实际应用等六种类型.

数学复习课以学生的问题为出发点，生成教学资源，我们不能苛求一节复习课教学功能的全面性，但是我们追求复习课功能的最大化，将复习课的课程目标分解到各节数学课，实现复习课提炼与迁移的教学功能.

三、精选例题，定位复习的“难度”

选择有代表性的题目，通过教材例题、习题的变式拓展，使问题深化，从中提炼数学思想和解题方法，研究高考题的命题思路，准确把握复习的难度.例题的选择处理考虑知识点的覆盖面，考虑所蕴含的数学思想方法，还要考虑学生的思维参与度.

教师应改变对集体备课无所谓的想法，不能以应付的态度对待集体备课，而应该全身心地投入.集体备课是一个经验的交流、沟通和分享的过程，讨论交流、信息整合是建构主义学习中不可或缺的过程，与新课程共同成长的数学教师，必须学会合作学习，实现彼此专业知识和共同建构教师合作文化，在不断总结自己的经验，吸纳他人意见的过程中，建构自己的知识体系，实现自己的专业发展.

例2 （高三周末练习）

已知对任意实数x，二次函数f（x）=ax2+bx+c恒非负，若a<b，则M=a+b+cb-a的最小值为.（这道填空题分值4分，但学生完成情况非常不好，平均得分1.87分，不少数学老师也觉得此题有难度）

鲍老师（高三年级备课组组长）：学生对这道题感觉十分棘手，因为平时经常接触到的是已知两个变量来求某一函数的最值，而这道题涉及三个变量.第一步应该是减少变量个数，重新审视一下题目，我发现二次函数f（x）=ax2+bx+c恒非负，

这表明b>a>0和b2-4ac≤0，而由M=a+b+cb-a的特点，感觉消去c较为合理.

由条件知b>a>0且b2-4ac≤0，即c≥b24a，

得M=a+b+cb-a≥a+b+b24ab-a≥1+ba+b24a2ba-1.

令ba=t，t>1，则M≥

1+t+14t2t-1=t-14+94（t-1）+32≥2t-14·94（t-1）+32=3，当且仅当t=4，即b=4a，c=4a时，M取得最小值3.

在实际教学中，这种解法是常规解法，但计算量太大，我發现M=a+b+cb-a的分子恰好是由f（x）=ax2+bx+c的赋值而来的，于是尝试凑配，

因为f（x）非负，故M=a+b+cb-a=4a-2b+c+3（b-a）b-a=f（-2）b-a+3≥0+3=3，当且仅当f（-2）=0，即f（x）=a（x+2）2，也即b=4a，c=4a时，M取得最小值3.

通过挖掘隐含条件，给出更简洁更准确的解答，让所有教师眼前一亮.像这样教师积极参与，特别是青年教师敢于讲出自己的观点，这在集体备课中要加以肯定和赞扬，只有老教师与青年教师相互促进、知识互补，才能实实在在地发挥集体备课的作用. 通过集体备课为年轻教师创造一个良好的学习氛围，让中老年教师在集体合作中吸纳新的教育思想、教学观念，把生动的传统教学经历补充到了集体备课之中，从而达到促进教师的成长、个人资源的整合、资源共享的目的.

社会互依理论启发我们：教师团队合作一方面可以使教师在相互交往中，汲取自身所需要的养分，发挥自身的优势，补充自己的不足;另一方面，可以通过相互的交流与互动，促使教师产生团体动力，发挥集体优势，进而提高教学质量，促进自身的专业发展.

参考文献：

[1]林伟，罗朝举，陈峥嵘.“思意数学”习题课教学模式的构建与实践[J].中学教研（数学），2020（11）：24-29.

[责任编辑：李 璟]