Adaptive Neural Observer-Based Nonsingular Super-Twisting Terminal Sliding-Mode Controller Design for a Class of Hovercraft Nonlinear Systems

Hamede Karami ·Reza Ghasemi

Received:7 July 2019/Accepted:5 September 2020/Published online:9 July 2021

©Harbin Engineering University and Springer-Verlag GmbH Germany,part of Springer Nature 2021

Abstract Designing a controller to stabilize maneuvering hovercrafts is an important challenge in amphibious vehicles.Hovercrafts are implemented in several applications, such as military missions, transportation, and scientific tasks. Thus, to improve their performance, it is crucial to control the system and compensate uncertainties and disruptions. In this paper, both classic and intelligent approaches are combined to design an observer-based controller.The system is assumed to be both controllable and observable.An adaptive neural network observer with guaranteed stability is derived for the nonlinear dynamics of a hovercraft,which is controlled via a nonsingular super-twisting terminal sliding-mode method.The main merits of the proposed method are as follows:(1)the Lyapunov stability of the overall closed-loop system,(2)the convergence of the tracking and observer errors to zero,(3)the robustness against uncertainties and disturbances,and(4)the reduction of the chattering phenomena.The simulation results validate the excellent performance of the derived method.

Keywords Hovercraft .Neural network .Observer .Terminal sliding mode .Nonlinear system .Nonsingular .Super twisting

1 Introduction

Hovercrafts,also known as air cushion vehicles(ACVs),are under actuated electromechanical vehicles that can move on water,land,and any kind of surface;this flexibility is due to the air cushion support underneath the vehicles,which minimizes friction with the bottom surface. Therefore, they are employed for applications such as helping flood refugees,transportation, and accessing impassable places (Rashid et al. 2012; Mutreja et al. 2015).Because of these extensive applications, it is crucial to control and solve the problems limiting these vehicles.

In both the modeling and control phases,hovercrafts may face challenges such as the inaccessibility of the variable states and the disturbance effects on the motion performance(Soneda and Ohtsuka 2002; Morales et al. 2015). Various observers have been designed to observe unknown parameters(Soneda and Ohtsuka 2002; Rigatos and Raffo 2015) and disturbances (Jeong et al. 2015; Xie et al. 2018; Lin and Wang 2017).Furthermore,observer design for nonlinear systems is an important subject in control engineering,and much effort has been channeled toward designing more efficient and up-to-date observers (Niu et al. 2004; Qiu et al. 2019; Nath et al.2019;Shah and Singh 2019;Huang et al.2019;Liu and Li 2019).

In recent years, artificial intelligence based on artificial neural networks has been used in several industrial applications.In the same way, neural network observers are widely used for the estimation of disturbances and unknown system parameters (Lau et al. 2019; Zhao et al. 2019; Wang et al.2018; Liu et al. 2018). This method has the advantages of parallelism during information processing,high accuracy with minimal neural units, and distributed knowledge representation(Resendiz et al.2008;Grigoryev et al.2010).

Artificial intelligence-based controllers that have been implemented on hovercrafts thus far include artificial neural network controllers and fuzzy controllers (Tunstel et al. 1994; Tanaka et al.2000;Wang et al.2012;Duan et al.2018).Some classic controllers include nonlinear Lyapunov-based tracking controller, PID controller, adaptive controller, and backstepping and second-order sliding-mode controller,which have been applied on hovercraft nonlinear systems(Aguiar et al.2003;Marconett 2003;Wang et al.2010;Ding et al.2017;Sira-Ramírez 2002).

The nonsingular fast-terminal sliding-mode methodology based on an adaptive neural network disturbance observer has been applied on flexible air-breathing hypersonic vehicles(Ma et al. 2019), and its performance is superior to the backstepping strategy. Terminal sliding-mode control is robust in the presence of both bounded disturbances and uncertainties and can stabilize the system in finite time(Hui and Li 2009;Mobayen and Javadi 2017).

The chattering effect in the sliding-mode control simulates the fast dynamics of sensors and actuators.This phenomenon damages the system actuator;therefore,in this context,a supertwisting algorithm is considered to eliminate the chattering effect(Boiko and Fridman 2005;Utkin and Poznyak 2013).

The nonlinear characteristics of the system and disturbances are estimated through experimental data in a neural network,and the weights of the layers are adaptively adjusted.This approach can enhance system robustness against disturbances and uncertainties (Zhou et al. 2012; Mobayen et al.2017; Abbaspour et al. 2017; Sharafian and Ghasemi 2017;Khoygani and Ghasemi 2016;Sharafian and Ghasemi 2019;Moghanloo and Ghasemi 2016).

Some finite-time control techniques that combine the fuzzy and cascade methods have been implemented for other marine vehicles.These methods also showed remarkable performance(Liang et al.2019;Wang and He 2019;Wang and Ahn 2019).

The main contributions of the paper are the use of a neural observer-based sliding-mode control,which has not been previously reported,and the use of a super-twisting algorithm to reduce the chattering phenomena.

In this paper, the terminal sliding-mode controller is adopted to control the ACV.The nonlinear dynamics considered in this paper induces lateral forces on the ACV,depending on the torque.Compared with the other studies that rely on the measurability of states of the ACV,a sensorless approach is derived in this paper. The neural observer is designed to identify the nonlinearity with high accuracy and guarantee the convergence of the observer to zero. In addition, the terminal sliding-mode controller based on the proposed observer is developed to satisfy the closed-loop system stability.

2 Hovercraft Dynamic Model

2.1 Model Description

The nonlinear dynamics adopted in this paper has been derived and identified in Liang et al. (2019). The equations of velocity components as shown in Figure 1 are presented below:

Figure 1 Sketch of air cushion vehicles model

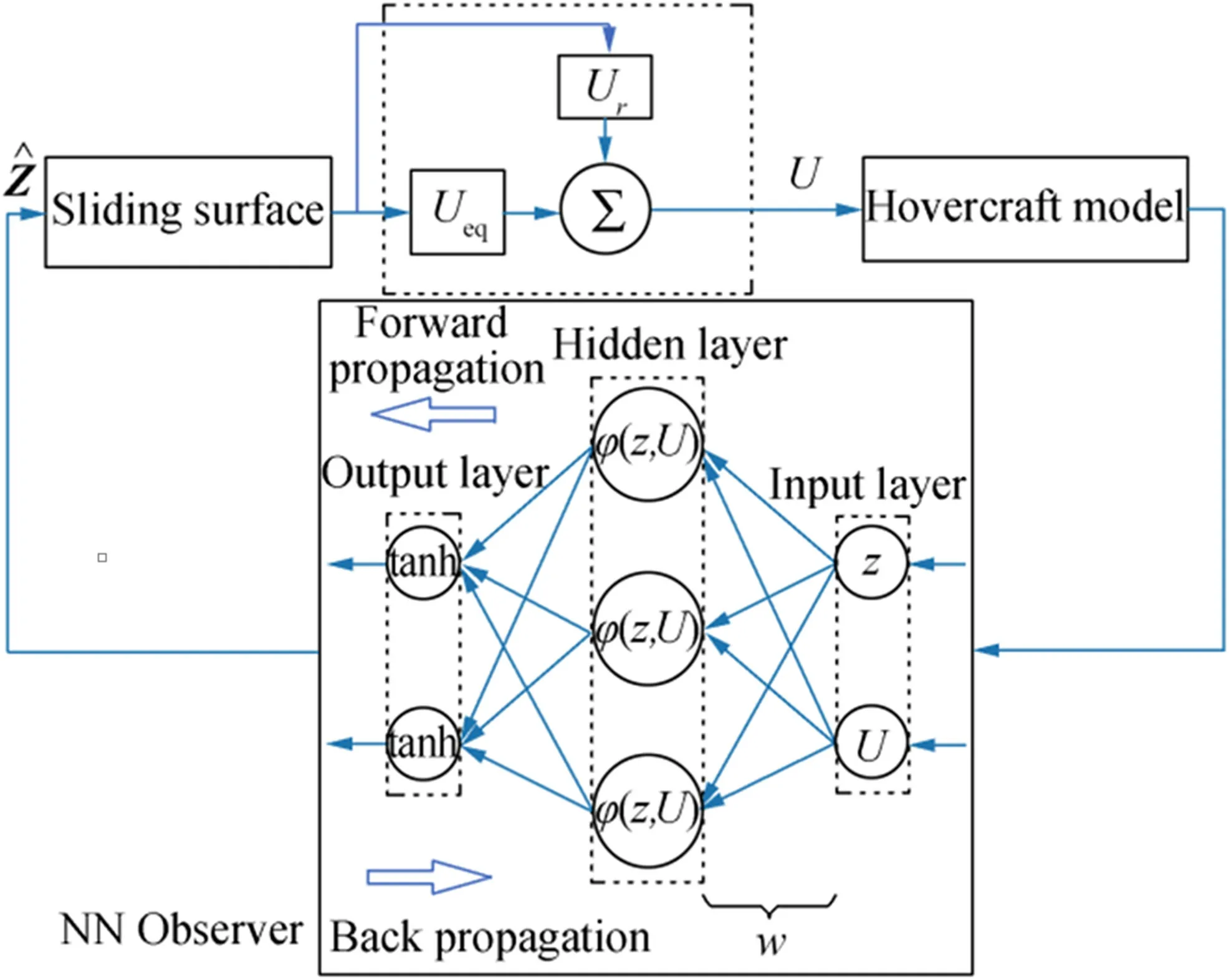
Figure 2 Proposed structure

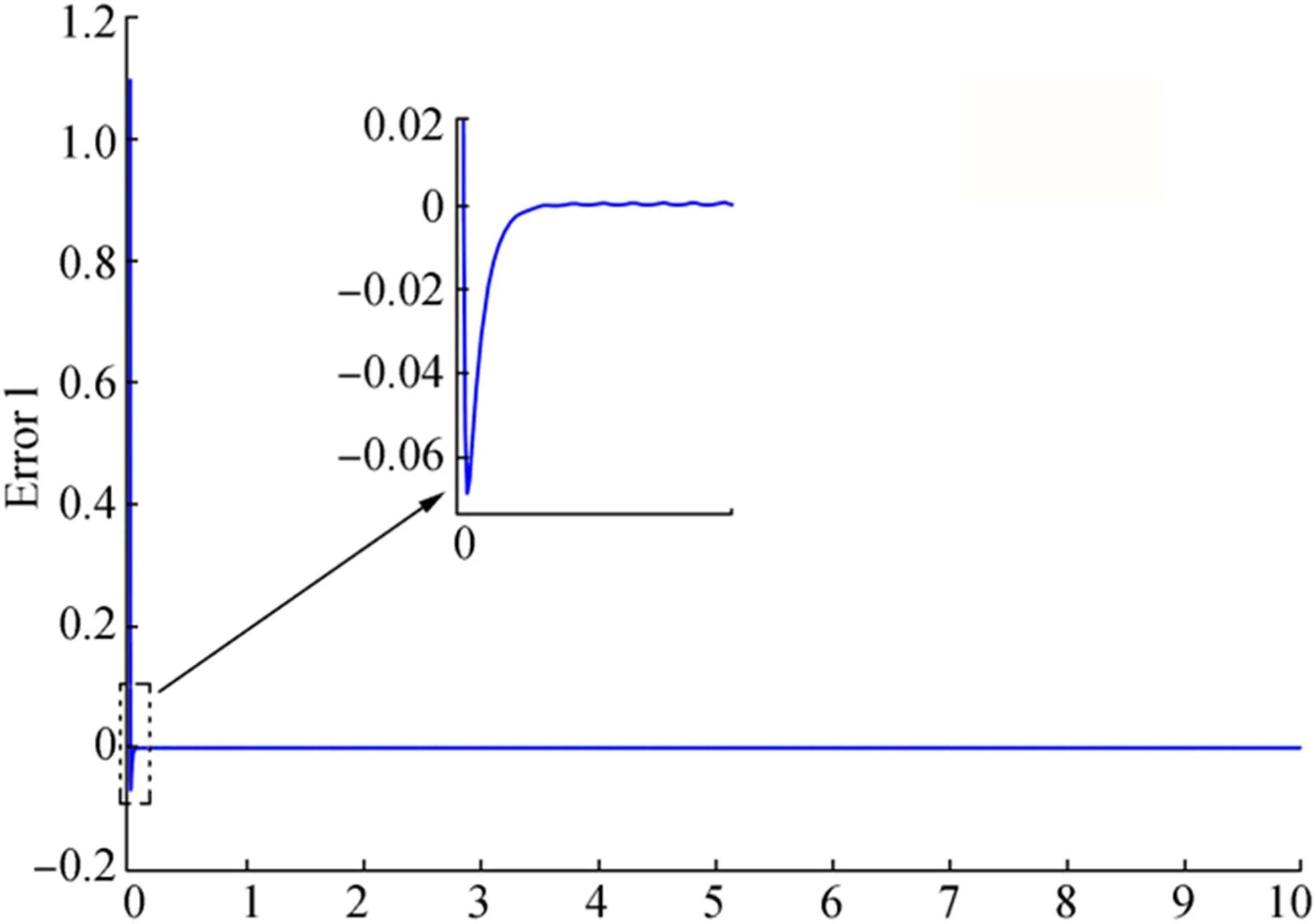
Figure 3 Estimation error of first state(z1)

Figure 4 Estimation error of second state(z2)

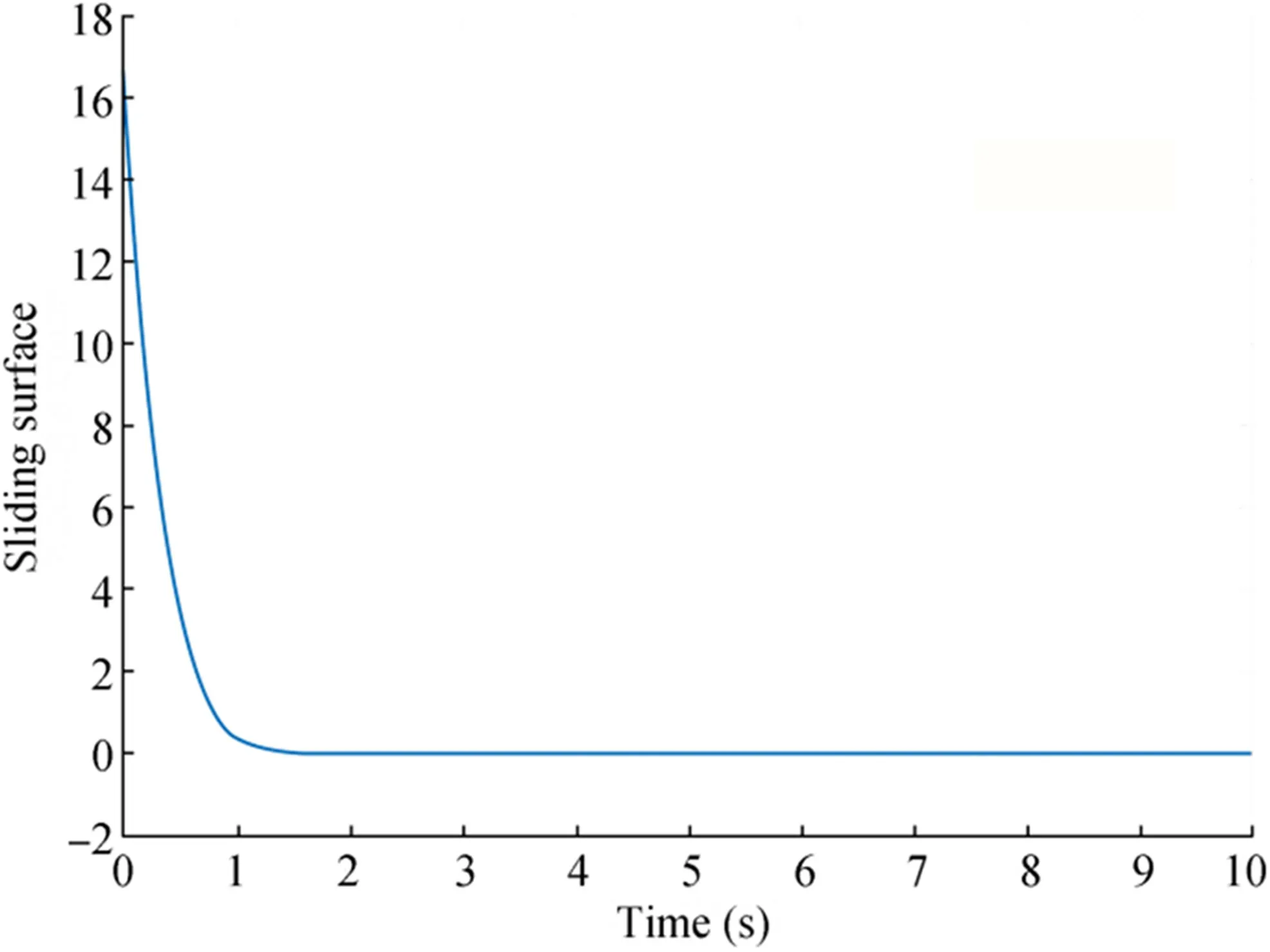
Figure 5 Sliding surface of the terminal sliding-mode controller

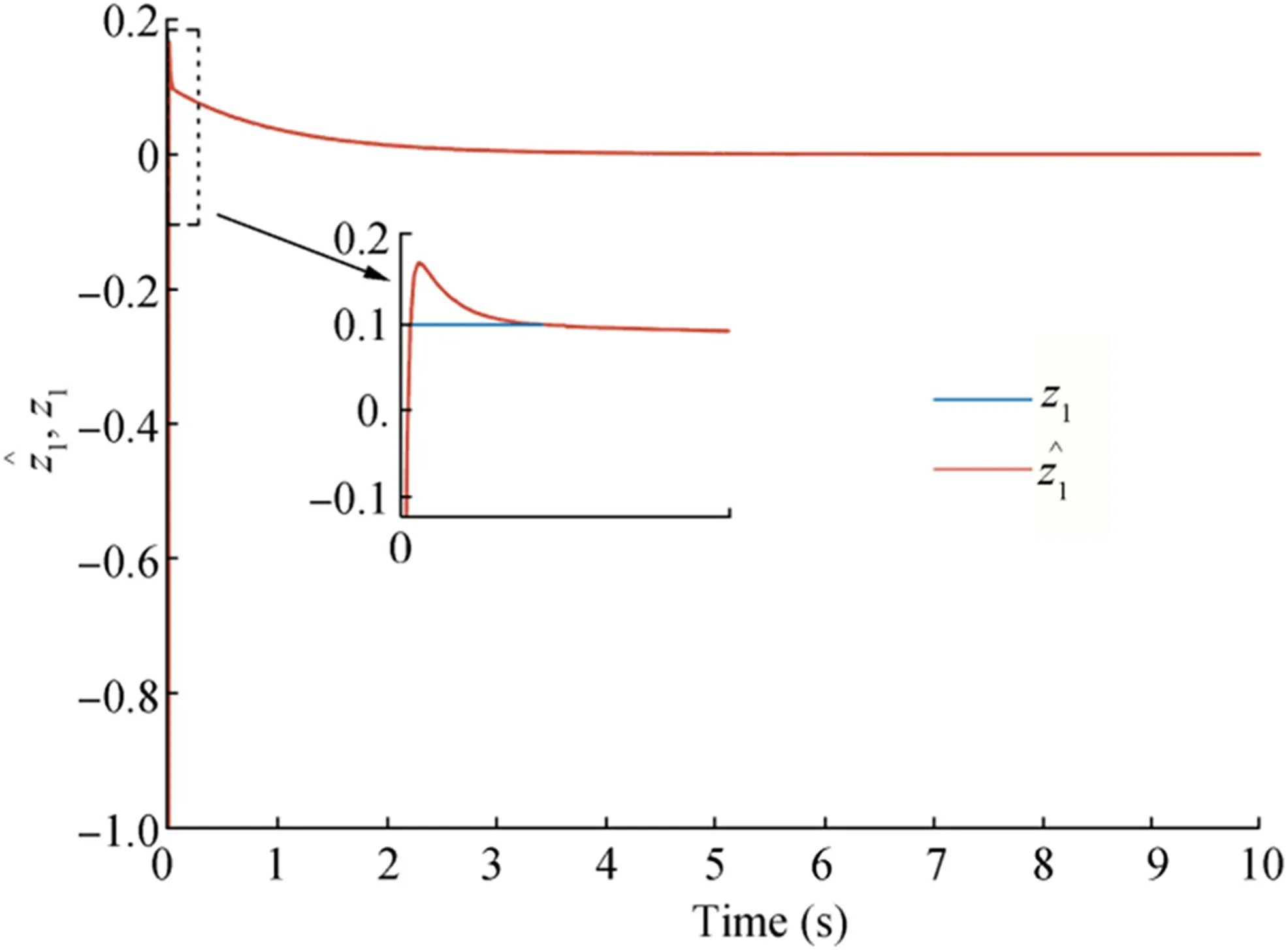
Figure 6 Estimation of z1 and real z1

Figure 7 Estimation of z2 and real z2

where u and v are the surge and sway velocities; r is the angular velocity; {du0, du, dv0, dv, dr0, dr}∈R are the friction and drag coefficients;a is the length of the arm from the center of mass to the rudder surface;T is the thrust force;and θ is the rudder angle;the coefficient bTscales the thrust input from[0,1]to force in Newton.

The model is actuated by the thrust force T and rudder angle θ,which are generated by propellers subjected to velocity drag forces.In these equations,the lateral force is induced on the system dependent on the torque.By some mathematical manipulations and particularization,the torque is disregarded in the mentioned equations.

The kinematics equation is as follows:

By substituting(2)into(1),the kinematics and the overall dynamics of the hovercraft is obtained as follows:

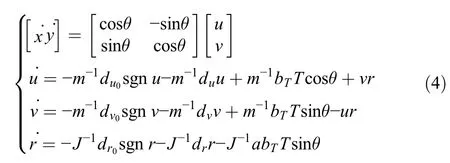
2.2 Model Transportation

To design the controller,the dynamics mentioned in(4)should be standardized in the strict feedback form;the diffeomorphism transformation should satisfy the following equation:

After some mathematical manipulations,a new state space is obtained as Eq.(6):

where A is a Hurwitz matrix and G(z,U)=f(z,U)-Az(t);G(z,U) contains both the uncertainty nonlinear and disturbance terms.

Without loss of generality, the following assumptions are considered:

Assumption 1:

Uncertainties that exhibit time dependence are omitted.

Assumption 2:(A,C)is observable.

3 Neural State Observer Design

3.1 Neural Network Observer Structure

Both the states and the inputs enter the neural network input layer.There are two input neurons.The hidden layer has three neurons and the output layer has two.The neuron numbers of the hidden layer are obtained by checking the neural network model response. The activation functions of the hidden layer and the output layer are considered a bounded hyperbolic tangent.The weights of the neurons are updated by the backpropagation algorithm:a neural network-based method that calculates the gradient of the error with respect to the weights for given inputs by propagating the error backward. The proposed algorithm considers the initial values as random small numbers around zero.The optimal parameters are used to estimate unavailable states.

3.2 Observer Formulation

The proposed observer,which is considered in this approach,is defined as(10):

3.3 Stability of Observer

The stability of the neural observer is proved in this section by considering the weight updating mechanism.

Proof:Equation(15)can be rewritten as follows:

Equations (13) and (16) are substituted into (18), and the following equation is obtained:

The proof is completed.

4 Controller Design

4.1 Nonsingular Terminal Sliding-Mode Control

Furthermore,the equivalent term of the rudder angle is as follows:

Therefore, these control inputs are applied to the system,and the stabilities of the overall closed-loop system, the observer,and the controller are proved.

4.2 Stability Analysis

Theorem 2 Consider the hovercraft,which is described by(4)and satisfies assumptions 1 and 2,and the observer derived in(9)based on the learning laws(15).The nonsingular terminal sliding-mode controller with the candidate sliding surface(24)and control inputs(25)-(28)make the system asymptotically stable, and the signals involved in the closed-loop system remain bounded.

Proof The Lyapunov function candidate is as follows:

To prove the stability of the closed-loop system, the time derivative of(29)should satisfy the following inequality:

By substituting(24)and its derivative into(30),the following equation is obtained:

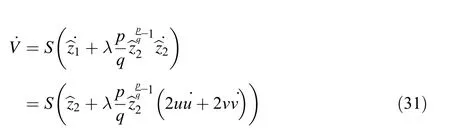
Based on Eq.(10),(31)is rewritten as:

Based on the control input in (25) and |S|=S sgn(S), Eq.(32)becomes:

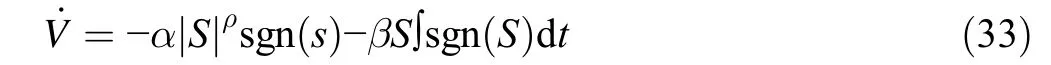
where α,ρ,and β are positive constants.

Through the control input mentioned in(25)-(28)and the application of some mathematical manipulations to(32),Eq.(33)leads to(34):

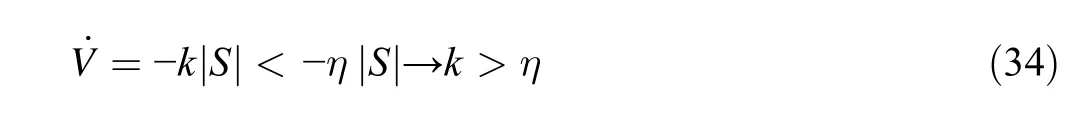
To satisfy Eq.(34),the inequality condition k＞η should be satisfied.Thus,the asymptotic stability of the system is proved and the proof is complete.

5 Simulation Result

The system was simulated using friction coefficients and system parameters in Liang et al.(2019)and Talebi et al.(2010).The controller,system,and observer parameters are presented in Table 1.

Table 1 System and controller parameters

The purpose of the simulation is to demonstrate the stability of the closed-loop system and the estimation accuracy.

The earlier mentioned control laws and observer were applied to the system,and the following results were obtained:

The convergence of the observer estimation error to zero is depicted in Figures 3 and 4.The results show the promising performance of the proposed neuro-observer.

The sliding surface of the terminal sliding-mode controller also converges to zero(Figure 5).

The first state of the system and its estimation are depicted in Figure 6.

The second state of the system and its estimation are depicted in Figure 7.

The convergence of the states and their estimations to the origin demonstrate the asymptotic stability of the closed-loop system in presence of the disturbances.

6 Conclusions

In this paper,a neuro-observer-based robust controller is designed for a class of nonlinear, controllable, and observable systems, and it can say that both classic and intelligent approaches are combined to design an observer-based controller.An adaptive neural network observer with guaranteed stability is derived for the nonlinear dynamics of a hovercraft,which is controlled via a nonsingular super-twisting terminal slidingmode method. The backpropagation algorithm is applied to update the weighting parameters due to the Lyapunov stability of the overall system. The super-twisting algorithm reduces the chattering phenomenon.Moreover,the Lyapunov stability of the closed-loop system,the convergence of both the tracking and observer errors to zero, and the robustness of the controller against uncertainties and disturbances are all achieved.The simulation results demonstrate the effectiveness of the presented methodology.