Analysis of Wave Energy Resources Around the Saint Martin Island in Bangladesh

Mohua Das · M. Rafiqul Islam · Tariqul Islam Shazeeb

Abstract Saint Martin Island is the only coral island and one of the well-known tourist spots in Bangladesh. Because of its geographic location, electricity cannot be supplied from the mainland through the electricity grid. Diesel generators and solar power are the only means of electricity generation presently available there. Surrounded by the sea, Saint Martin Island has the ideal conditions for wave energy extraction. In this research, numerical models have been developed using the Delft3D simulation software to determine the wave characteristics of different locations around Saint Martin Island. The results have been calibrated and validated against the data obtained from well-known data sources. The wave power densities have been calculated using the data obtained from the simulation models. The findings of the research show that the wave power density increases significantly from shallow water to deep water and a large amount of wave energy can be extracted during the summer and rainy monsoon seasons. The maximum hourly average value of wave power in 2016 has been determined to be 6.90 kW/m at location with a water depth of 27.80 m. Wave energy resources are also observed to be sufficiently stable with the coefficients of variation of wave power density less than 0.62, except for December, January, and May of that particular year. Moreover, the annual effective energies have been determined to be within the range of 36.57 to 57.28 MWh/m, which will be sufficient to meet the electricity requirement of the island communities.

Keywords Renewable energy · Ocean waves · Saint Martin Island · Delft3D · Wave power density · Stability

1 Introduction

Ocean waves are one of the highly predictable and available renewable energy resources that contain 15 to 20 times more energy per square meter in comparison with wind or solar power (Islam et al. 2014). Waves are generated by energy transfer from the wind to the water. However, depending on the wind speed, fetch length, and wind duration, the wave characteristics can vary. The power requirements of any country in the world can be partially fulfilled by utilizing its wave energy resources as a large amount of energy can be extracted from waves. However, mapping of wave energy is a prerequisite before its exploitation. As a result, several research activities have been conducted in many countries in the world to assess wave power potential. Some of these studies have been conducted using different data sources.These sources include the European Centre for Medium-Range Weather Forecasts (ECMWF) Re-Analysis (ERA)-Interim wavefield data (1979-2014) (Espindola and Araújo 2017; Kumar and Anoop 2015; Wan et al. 2017), ERA-40 wave reanalysis data (1957-2002) (Zheng et al. 2014), Radar Altimeter Database System (Yaakob et al. 2016), AVISO multisatellite altimeter dataset (Wan et al. 2015), and hindcast data from the SIMAR-44 dataset (Iglesias and Carballo 2010). Moreover, other studies used different numerical models, such as the third-generation wave model WAVEWATCH III, third-generation wave prediction model WAM(Aboobacker et al. 2017; Arinaga and Cheung 2012; Besio et al. 2016; Bouhrim and El Marjani 2019; Hughes and Heap 2010; Swain et al. 2017; Zheng et al. 2012; Zheng et al.2013), and Simulating Waves Nearshore (SWAN) model(Akpınar and Kömürcü 2013; Kim et al. 2011; Lavidas et al.2017; Liang et al. 2014; Monteforte et al. 2015; Morim et al.2016), to simulate nearshore wave energy propagation. Furthermore, in situ measured wave data based on buoy measurements were used for energy assessment (Kumar et al.2013). From all of these findings, different locations have been categorized into wave energy-rich, sub-rich, available,and indigent areas based on the values of the wave power density. For example, if the wave power density is greater than 2 kW/m, then the wave power resources are considered available; if the wave power density is greater than 20 kW/m, then the wave power resources are considered rich(Wan et al. 2015; Zheng et al. 2012, 2013, 2014). Moreover, the selection of suitable energy conversion techniques from the existing ones and the design of new energy converters have been made in many studies. The factors that have been considered in these studies include the characteristics of wave climate, annual storage of wave energy, monthly and seasonal variations of wave power density, and coefficients of variation (CV) of wave power data. For instance,Zheng et al. (2013) regarded significant wave height values greater than 0.5 m as exploitable based on the performance of several excellent wave power devices. Zheng et al. (2014)defined significant wave height values greater than 0.8 m as the effective significant wave height to assess the suitability of different regions for wave energy resource development. Furthermore, Wan et al. (2015) reported that the characteristics of wave climate with significant wave height ranging from 0.5 to 4.0 m and wave energy period ranging from 4-10 s are advantageous for energy conversion techniques. Moreover, Monteiro et al. (2016) reported that, for stable resources, theCVof wave power data should be less than 0.8. Although studies of wave energy assessment and exploitation are becoming well-known around the world,Bangladesh still lags in this context. This research is conducted to address such a crucial issue, where the potentials of wave energy extraction are thoroughly assessed around a well-known island in Bangladesh, i.e., Saint Martin Island.

In Bangladesh, the contribution of existing renewable energy resources (i.e., biogas, hydropower, solar, and wind)is less than 2% of the total power generation (Islam and Khan 2017). The Government of Bangladesh has undertaken a 5-year plan to generate 5% to 10% total power from renewable energy sources (Islam and Khan 2017). Thus, the proper utilization of wave power needs to conform to the plan of the Bangladesh government and help lessen the energy crisis. Furthermore, Bangladesh is blessed with the world’s longest natural sea beach and many islands surrounded by the Bay of Bengal. If the waves of the Bay of Bengal are properly utilized to produce electricity, then it can not only fulfill the total electricity demand to some extent but also enable access to electricity by the remote areas of the country. Before the exploitation of wave energy, studies of the characteristics of wave climate, total storage of wave power density, and feasibility of energy extraction projects in the coastal regions of Bangladesh need to be conducted. Thus far, only a few studies have been conducted to assess the wave energy of the Bay of Bengal. Islam et al. (2014) conducted a study of the waves generated in the Bay of Bengal at Cox’s Bazar, Chittagong, Bangladesh, and proposed an energy conversion method. In their study, they calculated wave power density using NRT-merged data. Finally, they concluded that a large amount of power could be generated from April to October and a moderate amount for the rest of the year. Moreover, Rahman et al. (2018) developed a model of the coastal region near Cox’s Bazar, Chittagong, Bangladesh, using the Delft3D simulation software. The output of their simulated model showed that a large amount of wave energy could be extracted from April to October. However,none of the previous research examined the percentage of exploitable significant wave height, stability of wave power,and total exploitable storage of wave energy resources.Moreover, no research activity has been conducted to examine the wave energy resources around the islands in Bangladesh. Given the geographic locations of the islands, supplying electricity from the primary electricity grid is expensive and difficult. Therefore, the generation of power using wave energy will help meet the power demand of the island communities. Of the islands in Bangladesh, Saint Martin Island is the most suitable for energy extraction operations because of its favorable geographic location and a moderate sea state value. Given the feasibility of wave energy exploitation projects, research to identify abundant wave energy resources and stable wave power regions around the island needs to be conducted.

Such an investigation was first conducted by Das et al.(2018). They investigated available wave energy per meter wavefront in one location (longitude, 92.317°; latitude,20.6°) near Saint Martin Island in Bangladesh from April 2016 to July 2016. In their study, they mainly concentrated on only one location at shallow water depth. However, the available wave power during peak season for tourists (October-February), variations of wave characteristics and wave power with the increase in water depths, selection of energyrich regions, and assessment of stability for the safe operation of wave energy converters (WECs), which are the main motivations of the present study, have not been assessed in their study.

Because no study of the selection of energy-rich regions near Saint Martin Island has been conducted, the present study is a novel one. This study concentrates on examining available wave power resources close to the island based on 23 observation points located at varying water depths,thereby providing an idea of the selection of regions rich in energy. Furthermore, this research provides information about the seasonal (i.e., peak and off-peak seasons for tourists) variations of wave characteristics, such as significant wave height, wave energy period, and wavelength in various water depths around Saint Martin Island. Such information is obtained from the output of the simulated model surrounding the Saint Martin Island executed using Delft3D. Thus,regions near the island with the highest wave energy potential have been selected for further assessment. Moreover,from the data extracted after simulation runs, histograms of significant wave height and wave energy period are developed. These histograms provide information about the percentage of waves having significant wave height greater than or equal to 0.5 m and wave energy period greater than or equal to 4 s to evaluate the suitability of WECs. This study also estimates and analyzes the percentage contribution of different sea states (defined by significant wave height and wave energy period) to the total wave power density,variability of wave power density, and total storage of wave energy potential to determine whether the resources are suffi-cient to diminish the energy crisis of the island communities.

The remainder of the paper has been organized as follows:Section 2 describes the overall methodology, including data collection, model development, and data analysis. Section 3 presents the characteristics of wave climate based on the output of simulation runs, estimation of wave power density,assessment of the stability of wave power, and calculation of the annual storage of wave energy. Section 4 provides the overall conclusions of the findings and suggestions for future.

2 Datasets and Methodology

In this study, the assessment of wave energy resources near Saint Martin Island has been done based on the results of coupled flow-wave models, which have been developed using Delft3D. Delft3D is a three-dimensional (3D) modeling suite that can execute numerical modeling of flows,sediment transport, waves, water quality, morphological developments, and ecology (Deltares 2017b). The modeling of flows and waves surrounding the island has been done using two modules of Delft3D (i.e., Delft3D-FLOW and Delft3D-WAVE). The Delft3D-FLOW module executes the multidimensional (i.e., 2D or 3D) simulation of nonsteady flow and transport phenomena resulting from tidal and/or meteorological forcing, including the effect of density differences due to a nonuniform temperature and salinity distribution (i.e., density-driven flow) (Deltares 2017a). The systems of equations used in this particular module include the horizontal equations of motion, continuity equations, and transport equations of conservative constituents (Deltares 2017a).Furthermore, in this modeling system, 3D Navier-Stokes equations are solved for incompressible free surface flow under shallow water and Boussinesq assumptions (Deltares 2017a). Another module of Delft3D, i.e., Delft3D-WAVE,has been used to simulate the growth of wind-generated short-crested random waves in deep, intermediate, and shallow waters and ambient currents (Deltares 2017c). The SWAN model is a third-generation spectral wave model,which is available in the Delft3D-WAVE module (Deltares 2017c). The SWAN model is based on the discrete spectral action balance equation and fully spectral (in all directions and frequencies) (Deltares 2017c). The SWAN model represents wave generation by wind, dissipation due to whitecapping, bottom friction, and depth-induced wave breaking,and nonlinear wave-wave interactions (both quadruplets and triads) explicitly with state-of-the-art formulations (Deltares 2017c). To set up flow and wave models using the modules,necessary data collected from different data sources have been used. To consider the effect of flow characteristics on wave simulation, coupling between the flow and wave modules of Delft3D has been done. Such coupled modeling is known as coupled flow-wave models. Finally, the simulation results have been compared with the data extracted using the Tide Model Driver (TMD) toolbox, data collected from the ECMWF website, and measured wave height data obtained from the Bangladesh Water Development Board (BWDB).Therefore, the entire process sequentially requires data collection, model setup, flow model calibration and validation,and verification of the results of coupled flow-wave simulations. These steps are illustrated in detail in the following subsections.

2.1 Data Collection

To generate the flow and wave models, five distinct types of data, i.e., bathymetry data, water level data, discharge data,wind data, and necessary boundary data of the wave grid,are required. The bathymetry data of the computational grid have been collected from the General Bathymetric Chart of the Oceans (GEBCO_2014 Grid) with the geographic coordinates 89.5° E-93.5° E, 18.5° N-23.5° N. The water level data of the downstream boundary of the flow grid have been extracted using the TMD toolbox at 1-h intervals for the years 2015 and 2016. The discharge data of the Lower Meghna River have been obtained from the BWDB at 3-h intervals. Finally, the wind data (i.e., components of wind velocity in theXandYdirections) and necessary boundary data of the wave grid have been collected from ECMWF ERA-Interim at 1-day intervals.

2.2 Model Setup

The steps that are involved in the setup of flow and wave simulation models consist of the generation of grids,bathymetry files, and input files that contain all of the necessary information required for defining the flow and wave simulation models. To perform the processes, two utility programs of Delft3D (i.e., RGFGRID and QUICKIN) and two modules of Delft3D (i.e., FLOW and WAVE) have been used. First, using the RGFGRID program, a computational grid (89.5° E-93.5° E, 18.5° N-23.5° N) surrounding the study region (i.e., Saint Martin Island) has been developed.The quality of the generated grid has been assessed based on the grid properties (i.e., aspect ratio and orthogonality),which show acceptable ranges. Afterward, to create the bathymetry file of the generated grid using the data extracted from the GEBCO_2014 Grid, the QUICKIN program has been employed. After creating the grid and bathymetry file,two input files, i.e., Master Definition Flow file (MDF-file)and Master Definition Wave file (MDW-file), have been generated. The MDF-file has been generated using the Delft3D-FLOW module with all of the necessary information required for flow simulation. The creation of the MDFfile requires input files, such as the grid and bathymetry file of the modeling area. Other information, such as simulation start and stop times, time steps for solving the governing equation of fluid flow, boundary conditions (i.e., discharge and water level data at grid boundaries), values of bottom roughness, viscosity, temperature, and density, and locations of the observation points have been specified in MDF-file.

Similarly, using the Delft3D-WAVE module, the MDWfile has been generated. This also requires input files (i.e.,grid and bathymetry file) and necessary input parameters(i.e., boundary conditions of the wave model, wind speed,wind direction) for the simulation of waves. Moreover, the coordinates of the observation points defined in the flow model have been specified in the wave model so that the necessary flow and wave parameters computed during the simulations could be extracted using specific time intervals.The observed locations have been selected in such a way that the assessment of available wave power density can be accomplished in both shallow water and deepwater regions.Seven observation points surrounding the island with a water depth of less than 8.0 m have been selected. Eight observation locations have been specified at depths ranging from 8.0 to 20.0 m, and eight other observation locations have been defined at depths greater than 20.0 m. The distances of these 23 selected locations from the island range from 1 to 30 km. The figures of the study region, computational grid,bathymetry of the computational grid, and location of the observation points are presented in Appendix.

Finally, coupling between the flow and wave models has been done. Such coupling enables the use of the flow characteristics during wave computation. Notably, the flow characteristics are obtained from the completion of the flow simulation. In the Delft3D-WAVE module, wave computation can be done using either the standalone wave model or the wave model coupled with the flow model (Deltares 2017c).In the standalone wave model, uniform values of water level and velocity are used (Deltares 2017c). In the coupled flow-wave models, as stated previously, wave computation uses the results of the flow simulations (Deltares 2017c).The computational domain of this research, as stated previously, covers the shoreline, nearshore, and offshore regions,and the interactions of waves and other processes, such as tides and surges, are enhanced when waves enter shallow water, as reported by Rosales et al. (2008). Moreover, wave properties, such as the steepness of the wave, significant wave height, and wave velocity, are modified because of the interactions of waves and tides. Thus, the coupled flow-wave models have been chosen instead of the standalone wave model so that the effects of the flow characteristics determined after hydrodynamic simulation are accounted for. The results of the flow simulation of the observed locations will be stored as a function of time in the history file, and the results of all grid points will be stored in map files. Furthermore, the results of wave simulation (i.e., significant wave height, peak wave period, and wavelength) will be stored as a function of time in the wave map file.

2.3 Data Analysis

From the developed flow simulation model, we obtain the water level data of all grid points. As measured water level data are unavailable, the accuracy of the water level data obtained from the flow simulation has been examined using the water level data extracted using the TMD toolbox. The results of the model show satisfactory consistency with the TMD data after several trials. In the next step, to extract the data of wave characteristics, coupled flow-wave simulations have been done. Data collected from two different sources(i.e., ECMWF ERA-Interim and BWDB) have been used to verify the simulation results. However, measured wave data are unavailable to verify the wave parameters, such as wave period and wavelength. Thus, only the values of significant wave height obtained from the simulation of coupled flow-wave models have been compared with the ECMWF ERA-Interim data and the measured BWDB data. A detailed description of the data analysis process is given in the following subsections.

2.3.1 Validation of the Flow Model

After setting up the model with the necessary information,we validate the flow simulation model. For this purpose, first,the water level data of our model are calibrated using the data obtained using the TMD toolbox. The calibration is done at an observation point (longitude, 92.317°; latitude, 20.6°) in July 2015. Notably, the simulation model has been run multiple times by changing bed roughness (i.e., Manning’s roughness factorn), which has been considered the calibration parameter.Each time, the simulation results at that particular observation point are compared with the TMD data. Finally, after running multiple simulations, forn=0.015, the simulated water level data show satisfactory consistency with the TMD data. Figure 1 presents the final comparison curve of the water level data. As shown in Figure 1, the dissimilarities of the two datasets are negligible and follow nearly the same trend.

After calibration, validation is done by running one more flow simulation in July 2016. From the output of the model, the water level data at an observation point (longitude, 92.286°;latitude, 20.522°) are compared with the data extracted using the TMD toolbox at the same observation point. As shown in Figure 2, the validation curve indicates that the results of the model show satisfactory consistency with the TMD data.

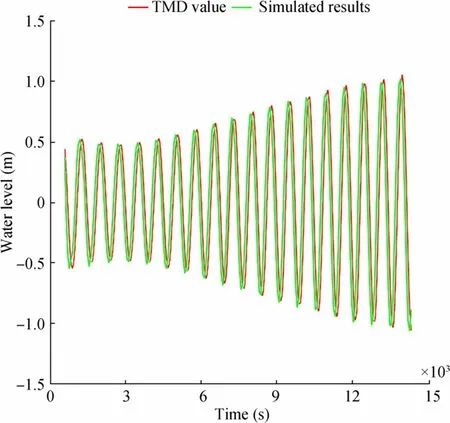
Figure 1 Calibration of the flow model

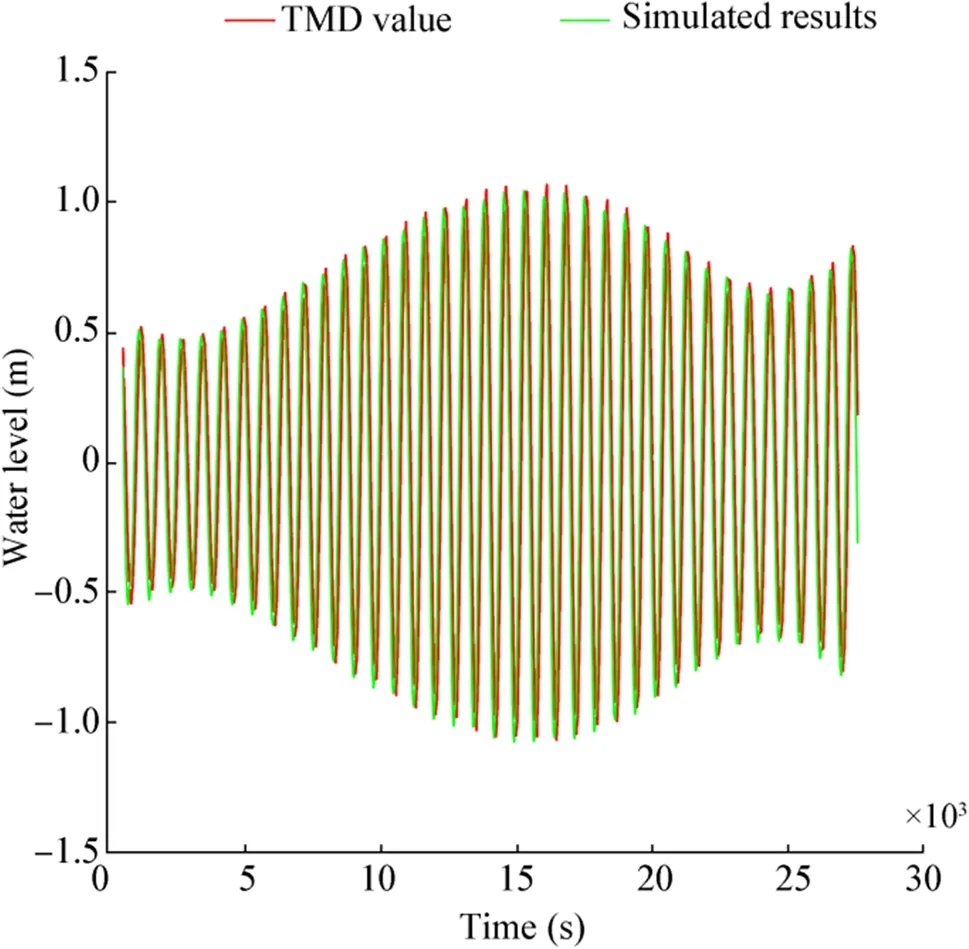
Figure 2 Validation of the flow model

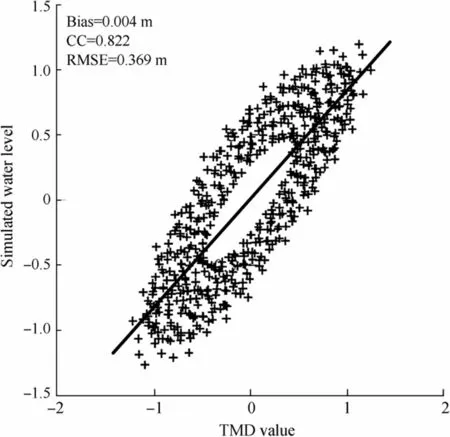
Figure 3 Scatter plot of the water level data obtained from the flow simulation versus the water level data extracted using the TMD toolbox

Figure 4 Comparison of significant wave height

Moreover, comparisons of water level data obtained from the flow simulation and water level data extracted using the TMD toolbox at the same location have been made based on the values of some error indices. Error indices, such as bias,correlation coefficient (CC), and root-mean-square error(RMSE), have been computed to verify the accuracy of the results of the model. The formulas used for the calculations are as follows (Zheng et al. 2013):

2.3.2 Comparison of the Wave Heights

After finalizing the input parameters for the stable flow model, simulation is performed by coupling the wave model with the flow model with space-varying and time-varying wind conditions. Simulation time starts from April 1, 2015,to July 31, 2015. The significant wave height data extracted from the output file at a location with 92.317° longitude and 20.6° latitude are compared with the significant wave height obtained from the ECMWF ERA-Interim reanalysis wavefield data.

Figure 4 shows the comparison curves, where the trend of variation of significant wave height is nearly the same as the data extracted from the ECMWF website. However,the magnitude varies slightly because of the unavailability of measured water level data during the generation of the flow model.

The accuracy of the simulated wave height data is verified by calculating the values of the error indices using Eqs.(1)-(3). The scatter plot of the significant wave height data obtained from the simulation of coupled flow-wave models versus the significant wave heights obtained from the ECMWF ERA-Interim reanalysis wavefield data is shown in Figure 5. Furthermore, Table 1 summarizes the values of the error indices. As shown in Table 1, the positive bias value of 0.149 m indicates the overestimation of the value of significant wave height by the coupled flow-wave model, i.e.,the average significant wave height obtained from the model is 0.149 m greater than the average significant wave height extracted from the ECMWF website. Furthermore, the CC indicates a strong uphill (positive) linear relationship. Thus,the models’ results can be considered quite satisfactory for further analysis.

Table 1 Quantitative comparison of the significant wave height data obtained from the simulation with the significant wave height data extracted from the ECMWF website

xiis the significant wave height data obtained from the ECMWF website,yiis the significant wave height data obtained from the simulation,Nis the total number of data points, and the overbar denotes the mean value of the two datasets.

The final comparison of the wave height data obtained from the coupled flow-wave simulations with the measured wave height data collected from the BWDB is performed.The comparison curves are illustrated in Figure 6. Because of the correction made to the datum level according to the BWDB datum level (i.e., 0.46 m below the mean sea level),negative values of wave height are observed in the comparison curves. As shown in Figure 6, the differences in the magnitude of the two datasets are insignificant and follow nearly the same trend.

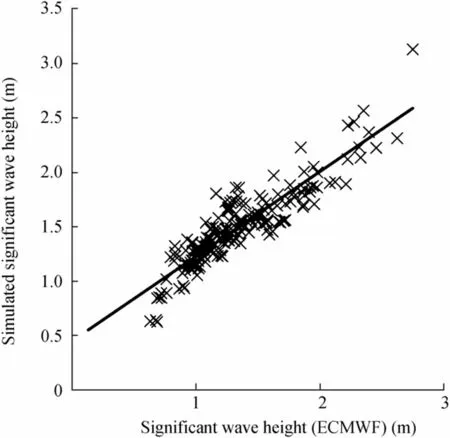
Figure 5 Scatter plot of the wave height obtained from the simulation versus the wave height obtained from the ECMWF website

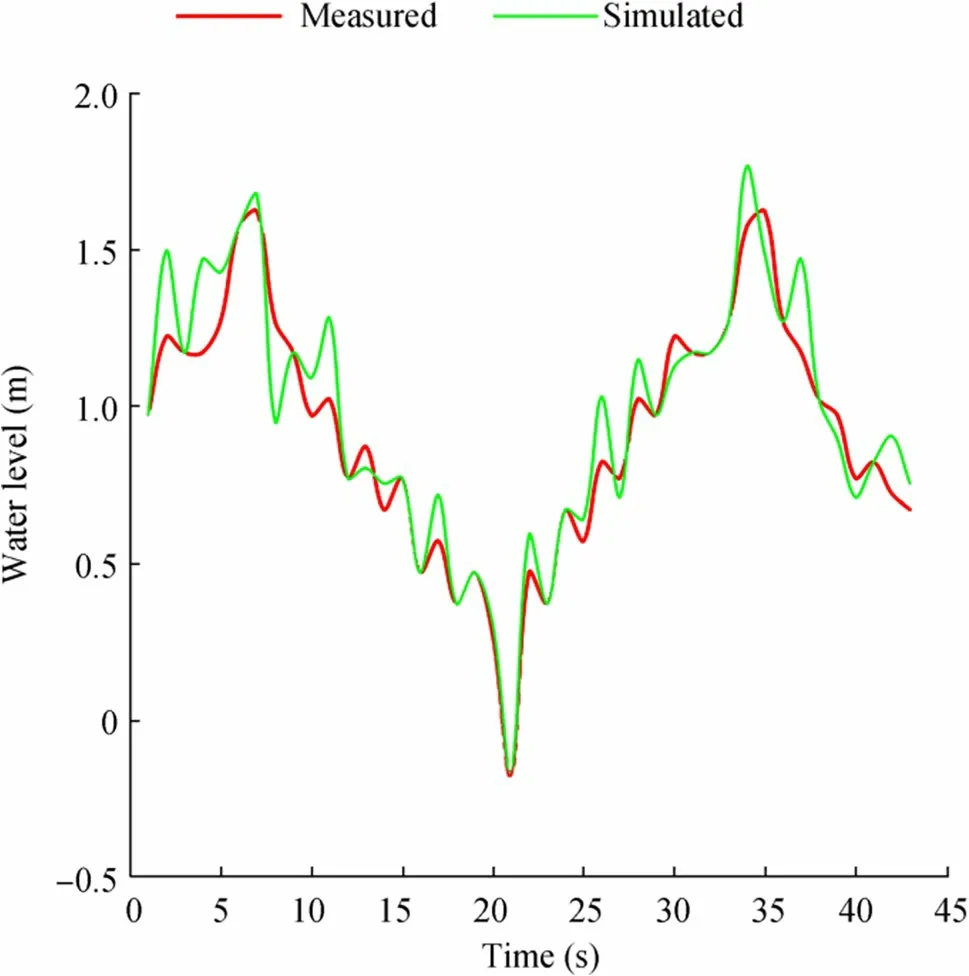
Figure 6 Comparison of the data obtained from the simulation with the data obtained from the Bangladesh Water Development Board(BWDB) (April 2015)

The accuracy of the models’ results is also evaluated based on the error indices (i.e., bias, CC, and RMSE). The scatter plot of the significant wave height data obtained from the simulation of coupled flow-wave models versus the measured wave height data obtained from the BWDB is shown in Figure 7. As shown in Figure 7, the bias value of 0.041 m indicates that the average value of the simulated wave height is slightly greater than the average wave height obtained from BWDB. Furthermore, the models’results show a good correlation with the BWDB data as the results are clustered around the line of best fit (CC=1.0)(Figure 7).

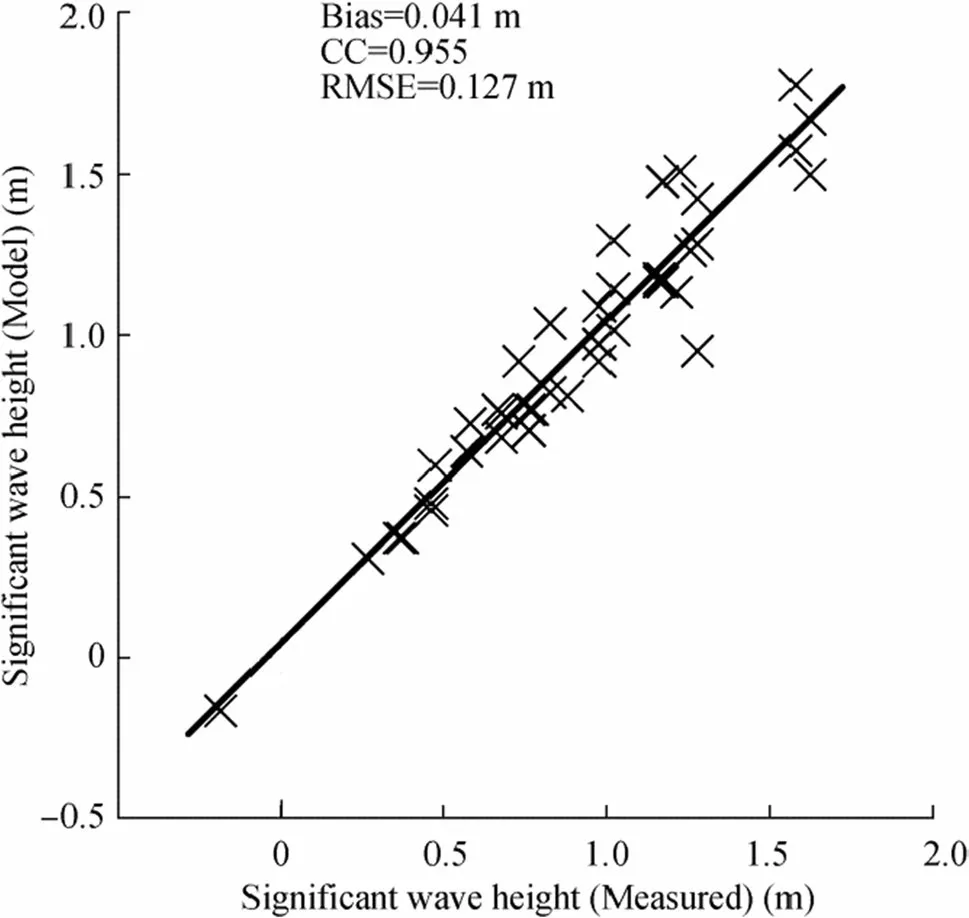
Figure 7 Scatter plot of the wave height obtained from the simulation versus the wave height obtained from the BWDB

Therefore, our results (i.e., significant wave height data)are consistent with the data of ECMWF ERA-Interim and BWDB. In the next section, the coupled flow-wave models are used to further assess the wave climate near Saint Martin Island.

3 Results and Discussion

In this section, analysis of the wave characteristics and estimation of the wave power density are conducted at different locations near Saint Martin Island. Initially, simulation runs are executed using our verified models. Based on the results (i.e., significant wave height and wave energy period), three locations at varying water depths are selected out of 23 observed locations having maximum values of significant wave heights and wave energy periods. Afterward,the selected locations are considered to calculate the wave power density, verify the stability of wave power density,and estimate the total storage of wave energy potential. The steps are described in detail in the following subsections.

3.1 Variation of the Wave Characteristics(Significant Wave Height and Wave Energy Period) at 23 Observation Points

Simulation runs of the coupled flow-wave models are executed in July 2016, and the results of the computational grid are stored in the wave map file. From the wave map file, significant wave heights and peak wave periods at 1-h intervals of the 23 selected locations (categorized into groups A, B,and C with the depth ranges of ＜8.0, 8.0-20.0, and＞20.0 m,respectively) are visualized and exported using the post-processing program of Delft3D (QUICKPLOT). Of the wave energy period, 90% is taken as the peak wave period because of the selection of the JONSWAP-type spectrum from the spectral space input parameters (Cornett 2008). Based on the output wave characteristic data, the hourly average values of significant wave height and wave energy period in July are calculated. Figures 8 and 9 show the graphical representations of the significant wave heights and wave energy periods of 23 locations with the increase in water depths. As shown in Figures 8 and 9, the maximum value of the average significant wave height (Hsig) is 1.70 m with an average wave energy period (Te) of 5.12 s at Location 1 in group A. Similarly, the highest values of the wave parameters are detected at location 14 (Hsig=1.86 m,Te=5.29 s) and location 20(Hsig=2.15 m,Te=5.54 s) in groups B and C, respectively.

Figure 8 Variation of the significant wave height at different observed locations

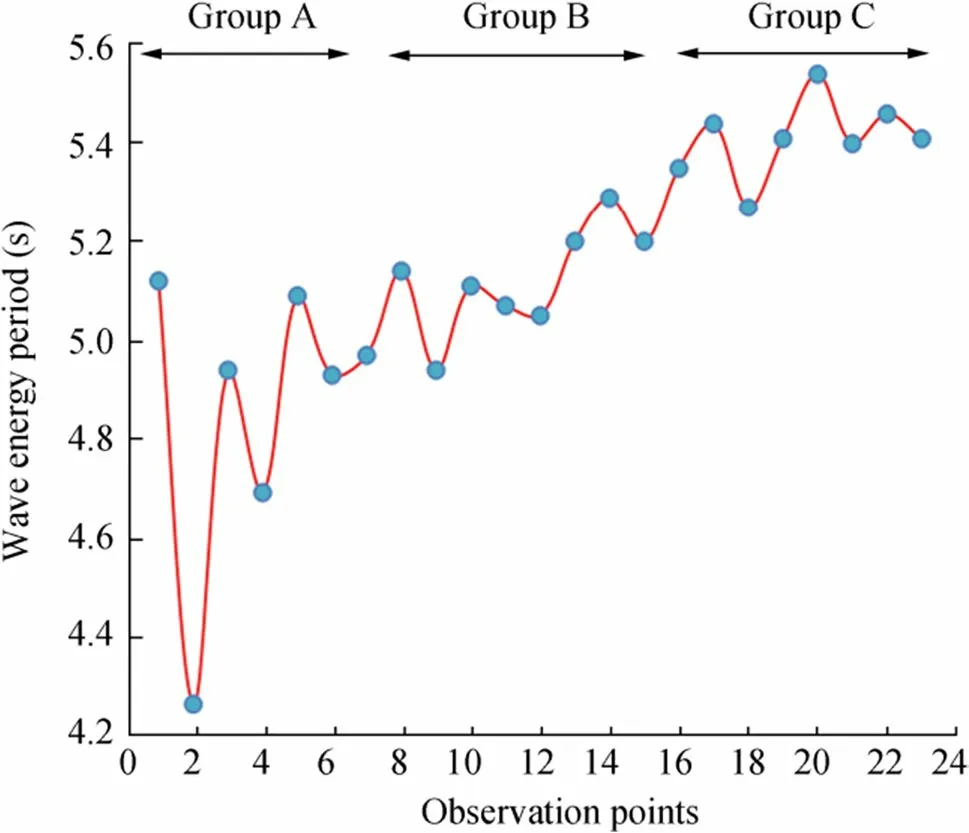
Figure 9 Variation of the wave energy period at different observed locations

As wave power density is proportional to the wave energy period and the square of the significant wave height (Jiang et al. 2019), three locations having maximum values of significant wave heights and wave energy periods from groups A, B, and C are selected. The selected locations are considered for the final assessment of the wave energy potential at varying water depths near the island. Table 2 shows the geographic coordinates, water depth, and distance from the island of the locations of interest.

3.2 Analysis of the Wave Characteristics of Three Observed Locations

The final simulation of the coupled flow-wave models is conducted from January 1, 2016, to December 31, 2016. A 1-h interval is set for the outputs of the specified locations of the computational grid. The results of the simulation are stored in history and wave map files. The necessary variables for computing wave power density are extracted using the post-processing program of Delft3D (QUICKPLOT).Descriptions of the variables (i.e., significant wave height,wave energy period, and wavelength) obtained from simulation results are given in the following subsections.

3.2.1 Analysis of the Significant Wave Height Characteristics

The variations of the significant wave height data at the three observed locations obtained from the models are presented graphically in Figure 10. The overall trend of the variations of the significant wave height is identical in three locations.Moreover, the variations of the significant wave height data follow an irregular or unsystematic pattern. The highest value of significant wave height (Hsig), which is 3.306 m at location 1, is recorded on May 21. The maximum values ofHsigat locations 14 and 20, i.e., 3.593 and 3.985 m, respectively, are also recorded on May 21. The minimum value of significant wave height at the three observed locations,which is less than 0.1 m, is recorded on January 17.

Figure 10 Simulated significant wave height for the year 2016

Table 3 lists the hourly average value of significant wave height for different months at specified locations. Theaverage value of significant wave height varies from 0.541 to 1.70 m at location 1. At location 14, the average value of significant wave height varies between 0.590 m and 1.861 m.At location 20, the average value of significant wave height fluctuates in the range of 0.670 to 2.145 m. The highest values of the hourly average wave height are recorded in July.

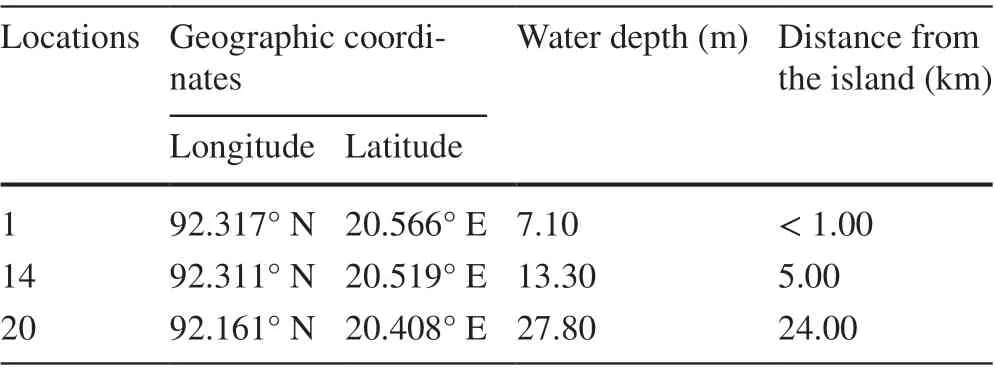
Table 2 Specifications of the three observed locations

Taking into account the safe and sound operation of WECs, waves with heights between 0.5 and 4.0 m are considered useful for the extraction of wave energy flux(Wan et al. 2015). Figure 11 illustrates the wave height histogram for location 1 plotted based on 8660 wave height data recorded from simulated coupled flow-wave models throughout the year 2016. The frequency of a specific range of waves is denoted by the area under the bar. The maximum number of waves of 3598 (i.e., ～ 41.55% of all occurrences)with significant wave height within the range of 1.0-1.5 m is recorded. Only 11 waves (0.13%) within the height range of 3.0 to 3.5 m are recorded. The frequency of significant wave height having a value greater than or equal to 0.5 m is estimated to be 92.03%.

Figure 11 Wave height histogram for location 1

Similarly, Tables 4 and 5 show the wave height frequency obtained based on the wave height data recorded from coupled flow-wave simulations of locations 14 and 20.As shown in Tables 4 and 5, the percentage occurrences ofsignificant wave height greater than 0.5 m are estimated to be 93.43% and 94.50% at locations 14 and 20, respectively.Furthermore, at location 14, the maximum number of waves of 3279 (i.e., ～ 37.86% of all occurrences) with significant wave height within the range of 1.0 to 1.5 m is recorded. At location 20, waves within the range of 1.5-2.0 m have the highest frequency (35.72% of all occurrences).

Table 3 Hourly average value of significant wave height for different months of the year 2016

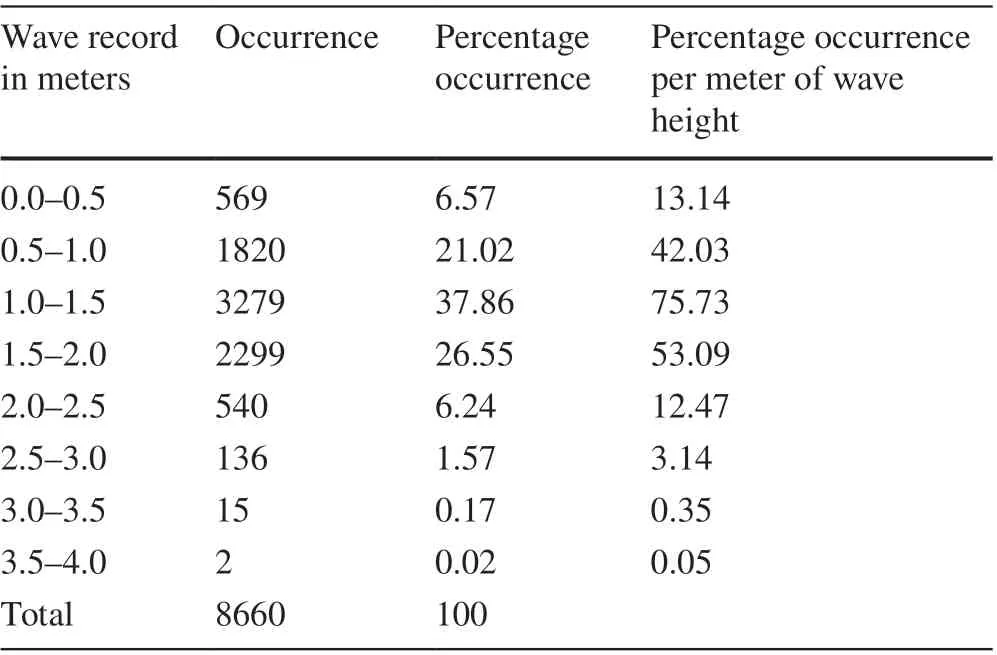
Table 4 Wave height frequency table for location 14

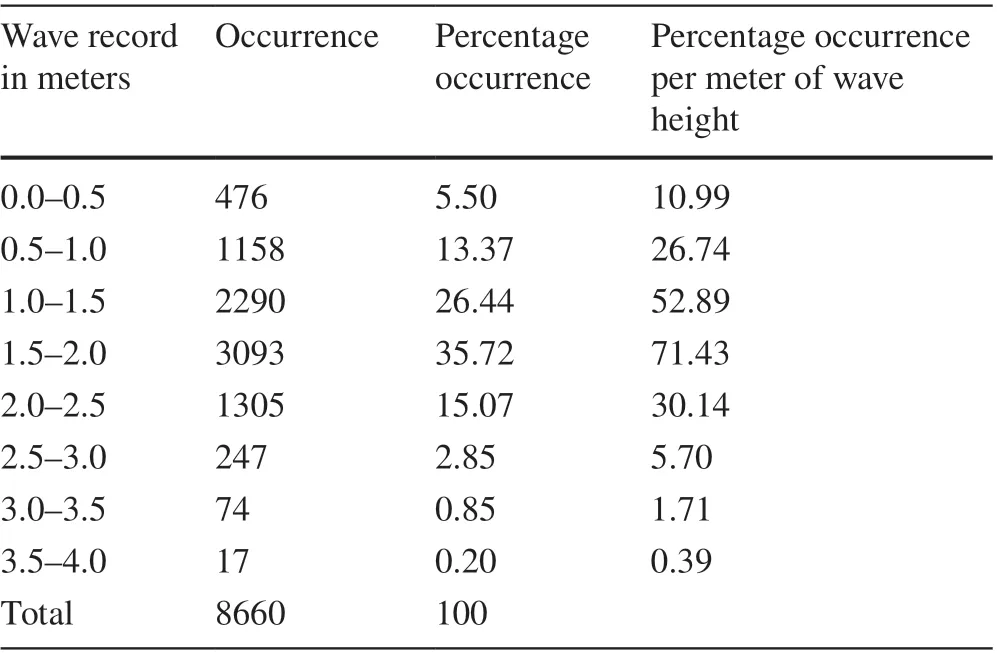
Table 5 Wave height frequency table for location 20

3.2.2 Analysis of the Characteristics of Wave Energy Period

From the simulation output, 8660 data of peak wave period at 1-h intervals for the year 2016 are stored. As mentioned earlier, the wave energy period has been calculatedconsidering the value is equal to the 90% of the value of the peak wave period. Figure 12 displays a graphical representation of the wave energy period at the three observed locations. The maximum values of the wave energy period are determined to be 6.70 s at location 1, 6.75 s at location 14, and 7.07 s at location 20. The highest values of the wave energy period at the three observed locations are observed at the same time (i.e., August 3). The minimum value of the wave energy period, which is less than 2 s, is observed on January 16. The increment of the value of the wave energy period is small with the increase in water depths. Furthermore, the patterns of variation of wave energy period with time are nearly the same for the three locations.

Figure 12 Simulated wave energy period for the year 2016

Wan et al. (2015) reported that wave energy periods within the range of 4 to 10 s are convenient for the energy extraction process. Thus, in this study, we attempt to determine the percentage of wave energy periods that occurred during 2016 that have a value greater than or equal to 4 s. Therefore, the histograms of the wave energy periods at the three observed locations are generated based on the calculated wave period data. Figure 13 illustrates the histograms of the wave energy periods at the three observed locations. As shown in the figure, the maximum number of waves (i.e., 36.71% and 35.53%of all occurrences at locations 1 and 14, respectively)with the value of wave energy period within the range of 4.0-5.0 s have been recorded. Similarly, at location 20, waves within the range of 5.0-6.0 s have the highest frequency. Moreover, the percentage occurrences of wave energy periods greater than or equal to 4 s are estimated to be 63.5%, 69.0%, and 73.5% at locations 1, 14, and 20,respectively.

Figure 13 Histograms of the wave energy period

Table 6 presents the information about the hourly average value of the wave energy periods for different months at the three observed locations. The maximum values of the average wave energy period are observed in June.The range of the variations of the wave energy period is determined to be 2.708 to 5.245 s at location 1, 2.796 to 5.398 s at location 14, and 2.876 to 5.682 s at location 20.

Table 6 Average values of the wave energy period (2016)

3.2.3 Analysis of Wavelength Characteristics

The wavelength data of the three observed locations obtained from the simulation of the coupled flow-wave models are presented in Figure 14. At location 1, wavelength varies in the range of 2.48 to 58.97 m. At location 14, wavelength varies from 2.86 to 63.08 m. At location 20, wavelength fluctuates from 3.04 to 78.14 m. The longest wavelengths at the three observed locations are recorded on August 3. Finally, at the three observed locations, the hourly average values of the wavelength for different months of the year 2016 have been calculated.Table 7 presents the hourly average value of wavelength at locations 1, 14, and 20. The highest average value of wavelength at the three observed locations is recorded in June.

Table 7 Average value of wavelengths for the year 2016

Figure 14 Simulated wavelengths for the year 2016

3.3 Wave Energy Density

3.3.1 Calculation Method of Wave Power Density

From the results of coupled flow-wave simulations, the values of the wave parameters (i.e., significant wave height, wave energy period, wavelength, and wave direction) are obtained at a specified time interval (1 h) for the year 2016. As the model does not provide the values of the wave power density directly, using the parameters stated previously, the wave power densities for all water depths have been calculated using the following formula (Wan et al. 2015, 2018):

Descriptions of the calculated wave power densities are given in the following subsections.

3.3.2 Assessment of the Wave Power Density and Characterization of the Wave Climate

The wave power characteristics of the observation points are presented in Figure 15. At location 1, the wave powerdensities vary from 0.003 to 3.668 kW/m and from 0.410 to 38.766 kW/m during the months January to March and April to June, respectively. From July to September, the wave power densities vary between 2.640 and 22.931 kW/m. For the rest of the months of the year, the wave power densities fluctuate from 0.058 to 8.065 kW/m.

Similarly, at location 14, for the months January to March,the wave power densities vary from 0.003 to 3.890 kW/m.For the months April to June, the wave power densities fluctuate between 0.568 and 50.383 kW/m. From July to September, the wave power densities vary in the range of 3.114 to 26.752 kW/m. From October to December, the minimum and maximum values of wave power are estimated to be 0.065 and 9.606 kW/m, respectively.

At location 20, the wave power densities vary from 0.004 to 5.521 kW/m and from 0.780 to 57.466 kW/m during the months January to March and April to June, respectively.From July to September, the wave power densities vary between 4.173 and 30.206 kW/m. For the rest of the months of the year, the wave power densities fluctuate from 0.053 to 12.140 kW/m. The highest value of wave power, which is 38.766 kW/m at location 1, is recorded on May 21. The maximum values of wave power at locations 14 and 20, i.e.,50.383 and 57.466 kW/m, respectively, are also recorded on May 21.

Figure 16 presents the hourly mean wave power for different months at the three observed locations and the comparative information about wave power density at different water depths. The hourly average values of wave power for different months of the year 2016 are also listed in Table 7.As shown in Figure 16 and Table 8, the wave power density increases significantly from shallow water to deep water. At location 1 (7.10 m water depth), the highest value of mean wave power per meter wavefront is 9.054 kW/m. The maximum values of the wave power density are 10.543 kW/m at a water depth of 13.30 m (location 14) and 13.271 kW/m at a water depth of 27.80 m (at location 20). That is, ～16.46%-46.90% increments of wave power density are observed with the increase in water depths. Furthermore, as shown in Figure 16, at the three observed locations, moderate wave power densities are observed in the summer (i.e.,March to June) and rainy monsoon (i.e., June to November)periods. In winter (i.e., December to February), the wave power densities are noticeably smaller.

After computing the wave power density of the observed locations, the directional distribution of waves and the percentage contribution of different sea states (defined by significant wave height and wave energy period) to the total wave power density are also determined. These will provide a reference for the design and evaluation of the performance of different WECs. The values of the wave direction of three observation points are extracted from the results of coupled flow-wave simulations. As shown in Figure 17a,the maximum number of waves (～ 52%) are predominantly observed between the WSW and WNW directions (247.5° to 292.5°) and the maximum value of significant wave height is 3.0 m. Moreover, 33% of the waves are observed between the SSE and SSW directions with the highestHsigvalue of 3.5 m. The directional distribution of significant wave height at Location 14 is nearly similar to that at location 1. As shown in Figure 17b, the dominant directions are W(49%) and S (35%) with the maximumHsigvalues of 3.0 and 4.0 m, respectively. At location 20, the dominant direction of 48% of the waves is S (157.5° to 202.5°) and the highestHsigvalue in this direction is 4.0 m. Furthermore, 36% of waves are observed between the WSW and WNW directions(247.5° to 292.5°) and the maximum value of significant wave height in this direction is 3.5 m (Figure 17c). Finally,Tables 9, 10, and 11 illustrate the bivariate distribution of occurrences corresponding to the sea states defined byHsigandTe. At location 1, sea states with the range of significant wave height between 1.0 and 2.5 m and wave energy period with the interval of 4.0 to 6.0 s have the greatest contribution(～ 80%) to the total wave power density (Table 9). Similarly,as shown in Table 10, at location 14, the dominant intervals of significant wave height and wave energy period are 1.0-2.5 m and 4.0-6.0 s, respectively (～ 76% of the total contribution). At location 20 (Table 11), sea states with the greatest contribution to energy have significant wave heights with the interval of 1.0 and 3.0 m and energy periods between 4.0 and 7.0 s. Tables 9 to 11 show that significant wave heights greater than 3.0 m and less than 1.0 m do not contribute much to the total wave power density.

Figure A1 Computational grid

Figure 15 Wave power at the three observed locations

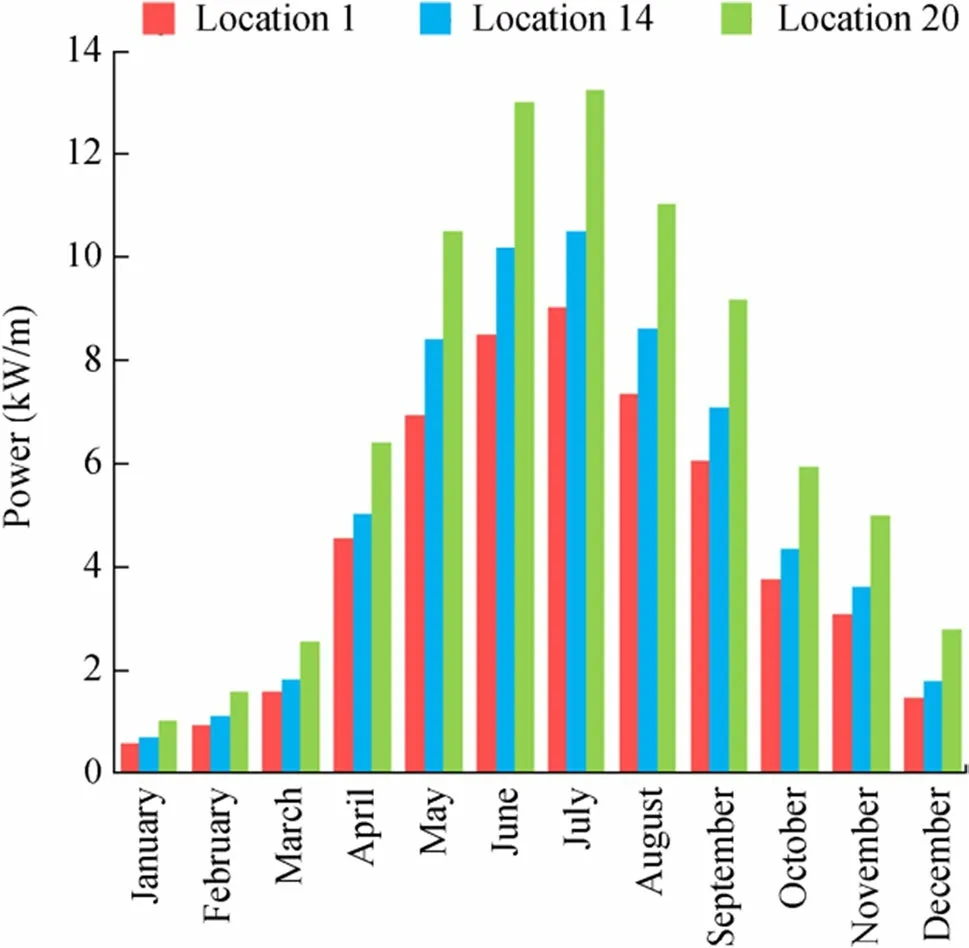
Figure 16 Variation of the wave power density with depth

Figure 17 Directional distribution of significant wave height

3.4 Variability of Wave Power Density

To assess the suitability of wave energy conversion systems, the temporal variability of the wave power data of the study regions needs to be determined. Several indices,such asCVof wave energy and monthly and seasonal variabilities of wave power, are used to evaluate the variability of the wave power and assess the stability of wave energy resources. Monteiro et al. (2016) reported that, for stable resources, theCVvalue should be less than 0.8 (i.e.,smaller values signify more stable wave energy resources).Moreover, moderately unstable wave power resources haveCVvalues within 0.8-0.9. Furthermore,CV＞0.9 indicates that the resources are unstable. Using the following formula, theCVvalue of wave power is estimated (Wan et al.2015):

Table 12 presents theCVvalues for different months.As shown in the table, except for December, January, and May, the wave energy resources satisfy the stability criterion (i.e.,CVvalues between 0.240 and 0.617) for energy conversion for the rest of the months of the year.

Table 8 Hourly average value of wave power

The monthly variability index (MV) and seasonal variability index (SV) can be defined as follows (Wan et al. 2015;Bouhrim and El Marjani 2019):

wherePMmaxandPMmindenote the values of the mean wave power density of the most and least energetic months,respectively. Similarly,PSmaxandPSmindenote the maximum and minimum values of the seasonal mean wave energy density, respectively, andPyeardenotes the annual mean wave power.

The values of the monthly and SV indices at the three selected locations are presented in Table 13. As shown in Table 13, both monthly and SV indices decrease with the increase in depths (locations 1-20). The values of the MV index indicate that the range of variation of the mean wave power densities for different months of the year 2016 is close to twice that of the corresponding annual mean wave power densities of the observed locations. Therefore, the monthly variation of wave power is significant and indicates the moderately fluctuating values of the wave power density of those three locations. Moreover, the SV index values are significantly lower than the MV index values. Small values of SV indicate an insignificant seasonal variation of wave power densities in relation to the annual mean wave power density.

Table 9 Characterization of wave energy resources in terms of significant wave height and wave energy period at location 1

Table 10 Characterization of wave energy resources in terms of significant wave height and wave energy period at location 14

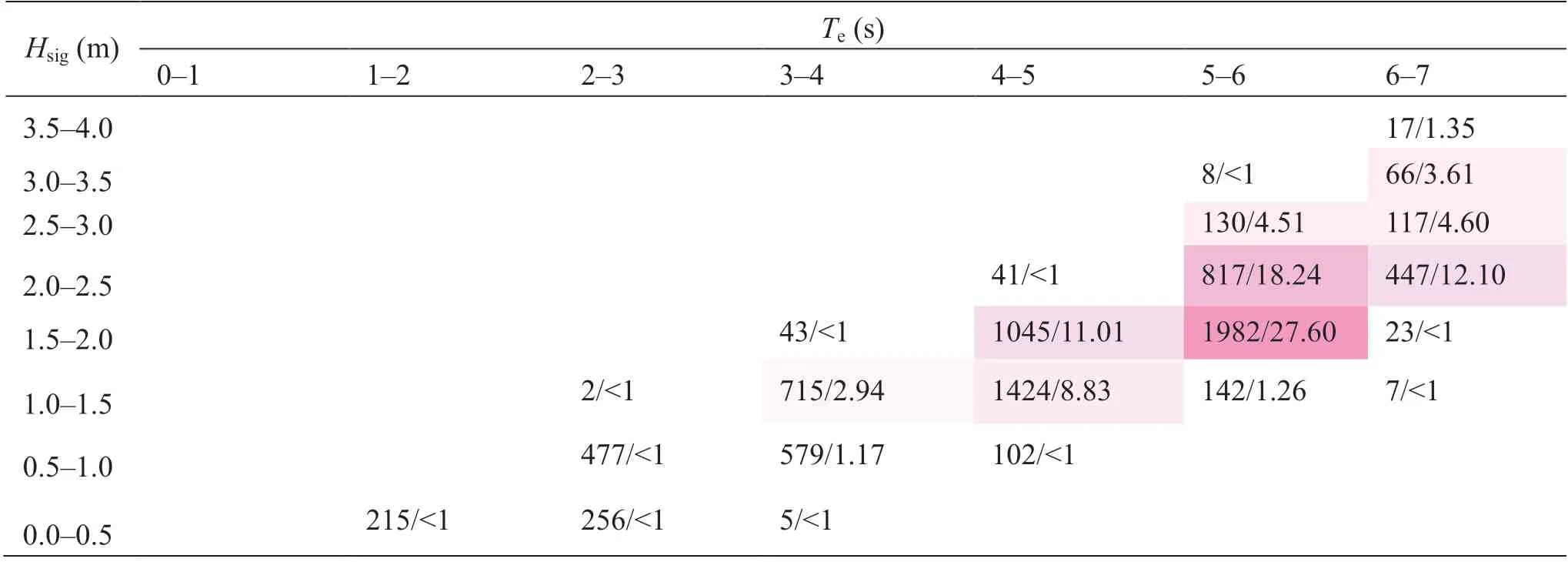
Table 11 Characterization of wave energy resources in terms of significant wave height and wave energy period at location 20

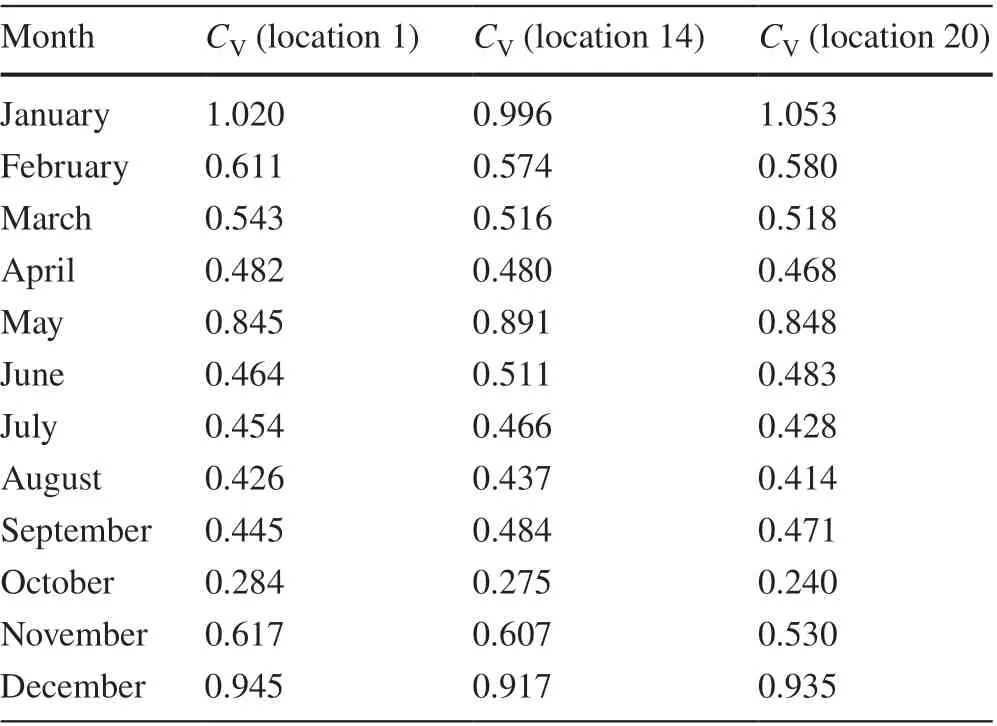
Table 12 Coefficients of variation of wave power

Table 13 Monthly and seasonal variability indices of wave power

3.5 Total Storage of Wave Energy Potential

The total storage of wave energy potential in 2016 is calculated using the following formula (Wan et al. 2015):

whereEeis the annual effective energies,Pavgis the annual mean wave energy density, andUHsigis the frequency of the significant wave height being greater than or equal to 0.5 m.

At location 1, the frequency of significant wave height having a value greater than or equal to 0.5 m is determined to be 92.03%. Furthermore, the annual mean wave energy density is calculated as 4.53 kW/m wavefront at that location. Similarly, the frequencies of the specific range of waves are 93.43% and 94.50%, respectively, and the annual mean wave power densities are calculated as 5.31 and 6.90 kW/m,respectively, at locations 14 and 20. Using the previously mentioned formula, the annual effective energies per meter wavefront are determined to be 36.62 MWh at location 1,43.58 MWh at location 14, and 57.28 MWh at location 20.

4 Conclusions

In this study, we attempt to estimate the wave energy resources at different locations around Saint Martin Island in Bangladesh using simulation modeling. Three locations with maximum wave characteristic values at varying water depths are selected from 23 locations near the island. In the selected locations, more than 90% of all occurrences have significant wave heights greater than or equal to 0.5 m. Moreover, the percentage of the wave energy period having values greater than or equal to 4 s varies between 63.5 and 73.5 in these locations. This information about significant wave height and wave energy period will be essential in designing new WECs suitable for energy extraction from the three observed locations in the future. Notably, the hourly average values of the wave power density are estimated to be 4.53 kW/m wavefront at 7.10-m water depth and 5.31 and 6.90 kW/m wavefronts at 13.30- and 27.80-m water depths, respectively.Thus, the wave energy densities in the selected locations fulfill the criterion of exploitable wave energy (Pw≥2 kW/m).Furthermore, the mean wave energy densities from April to October are higher than those of the rest of the months of the year, which can be attributed to heavy rainfall during these months. Finally, the annual effective energies are estimated to be 36.62 MWh/m at location 1, 43.58 MWh/m at location 14, and 57.28 MWh/m at location 20. Hence, the findings of this research show that around the island in different water depths, 36.62 to 57.28 MWh energy can be obtained across each meter of the wavefront, whereas ～55.4 to 61.5 kW energy is required daily (485.30 to 538.74 MWh/year) to reduce the energy crisis of island communities, as reported by Sarker et al. (2017).

Therefore, an important scope of future research can be the design of suitable and cost-effective WECs and the determination of the required number of energy conversion devices that will be installed to fulfill the energy requirement. Moreover, this study mainly focused on the theoretical wave power available for the three observed locations near the island. Furthermore, the wave rose and wave scatter diagrams provide information about the directional distribution of waves and bivariate distribution of occurrences of wave power corresponding to the sea states defined by significant wave height and wave energy period. However,the actual amount of exploitable electric power depends on the characteristics of different WECs, as reported by Silva et al. (2013). Hence, another scope of future research can be the determination of the electric power outputs of different shoreline, nearshore, and offshore devices.

Thus, this study analyzes the potential and feasibility of energy resources around Saint Martin Island to meet the local energy demand, and the results are promising. However, in comparison with global wave energy resources,these regions are not rich. Nevertheless, the design of suitable and cost-effective WECs would enable the implementation of the extraction process.

Appendix

This appendix contains some necessary information about the computational grid, bathymetry, and observation points. A computational grid surrounding the study region is generated using the Delft-3D RGFGRID program. The geometric coordinates of the computational grid are 89.5° E-93.5° E, 18.5° N-23.5° N, and the grid cell size is 2 km×2 km (Figure A1). Figure A2 shows the depth at different locations of the computational grid,where negative values indicate elevations from the mean sea level and positive values indicate water depth from the mean sea level. The maximum water depth of the study region is 2.317 km. Figure A3 shows the positions of the observed locations.

Figure A2 Depth of the computational grid

Figure A3 Locations of the observation points around Saint Martin Island