基于无人机中继的星地认知网络波束成形算法

李艳丽，林志，王子宁，许拔，程铭，欧阳键

（1.南京邮电大学通信与信息工程学院，江苏 南京 210003；2.国防科技大学电子对抗学院，安徽 合肥 230037；3.国防科技大学六十三研究所, 江苏 南京 210003）

1 引言

跟地面通信系统相比，卫星通信因为其覆盖范围广、通信容量大以及不受地域影响等优势，能够满足未来通信网络对全时域全地域通信的要求，被认为是下一代移动通信系统的核心技术之一，受到了国内外学者的广泛关注[1-2]。然而卫星通信易受遮蔽效应的影响，通信质量下降，因此研究人员提出采用中继技术解决卫星通信质量不稳定问题。相比于常见的地面基站，无人机具备成本低廉、悬停能力、易于部署以及系统维护方便等特有优势。在地面设施受到自然灾害损坏或者军事通信要求无线网络可移动情况下，采用无人机作为中继的网络更受青睐[3-7]。因此基于无人机中继的卫星网络受到了国内外学者的广泛关注。例如，参考文献[8]提出一种以无人机为中继的卫星网络，并对无人机中继进行选择，推导出系统的中断概率；参考文献[9]考虑无人机作为空中中继协助卫星下行链路传输的场景，研究了系统的能效最大化传输问题；参考文献[10]针对无人机为中继的星地网络在满足上行传输可靠性以及低功耗要求下，提出了一种能效资源分配算法。尽管为基于无人机中继的卫星网络提供了框架，参考文献[8-10]只是在频谱等资源理想配置情况下，研究了网络的资源分配、系统性能。实际上，随着无线设备以及物联网终端的大规模部署，频谱资源受限问题严重限制了网络的服务能力。与此同时，传统的频谱管理方法不够灵活、合理，例如无人机通常采用的S频段和L频段[11-12]，被许多其他无线网络（例如Bi-Fi、蓝牙）占用，导致频谱资源更加紧张。为了充分利用频谱资源，提升系统吞吐量和用户容量，认知无线电（cognitive ra2io, CR）技术应运而生[13]。CR技术通过动态管理频谱资源实现了主网络和次级网络的频谱资源共享。CR是解决无线通信中频谱资源稀缺和利用率不足问题的有效技术之一[14-16]，在星地网络中也得到了应用。参考文献[17]针对基于无人机中继的星地认知网络下行链路，提出了一种联合波束成形（beam+orming, BF）方案，解决了网络在发射功率受限条件下的安全传输和能效问题。虽然参考文献[17]对基于无人机中继的星地认知网络做了较为深入的研究，但其假设已知理想信道状态信息（channel state in+ormation, CSI）。在实际通信系统中，由于快衰落等因素影响，获得理想CSI比较困难[18]，一般只能获得统计 CSI。在统计 CSI情况下，基于无人机中继的星地认知网络信息传输问题研究还面临着巨大的挑战，目前相关研究工作甚少。

本文考虑地面网络作为主网络，采用无人机中继的卫星网络作为次级网络，研究了基于无人机中继的星地认知网络的BF算法。具体而言，首先在无人机中继发射功率和主用户干扰功率受限条件下，建立次级用户信干噪比最大化的优化问题。接着在已知次级用户统计CSI条件下，提出两种BF方案进行求解：一种为基于迭代的BF算法，根据广义瑞利商求解具有迭代常数的BF权矢量表达式，然后利用迭代得到迭代常数的最优值，进而求解出的BF权矢量。考虑到基于迭代的BF算法具有较高的计算复杂度，为了减少求解问题的计算量，提出了另一种基于迫零的BF算法，并推导出相应的BF权矢量解析解。最后，仿真验证了所提两种波束成形方案的正确性与有效性。

2 系统模型

如图1所示，基于无人机中继的星地认知网络由主网络和次级网络构成，主网络由基站和主用户组成，次级网络由一个地球静止轨道（geostationary earth orbit，GEO）卫星、一个无人机中继和次级用户组成。其中，卫星配置多馈源单反射面天线，无人机中继配置N根天线，基站配有M根天线，其他终端均配备单根天线。

图1 基于无人机中继的星地认知网络系统模型

2.1 信道模型

考虑空间损耗、降雨衰减和卫星波束增益的影响，卫星下行链路的信道矢量h∈ CN×1通常表示成[1]：

其中，φm∈CN×1中的各元素在[0,2π)均匀分布。r=[rm1,rm2,… ,rmN]T表示雨衰系数，以2B为单位表示的=20lg (rmn)服从对数正态随机分布～ CN (μ,),1≤n≤N，μ和σr取决于卫星的通信频率、极化方式和用户的位置。b=[bm1,bm2,… ,bmN]T表示点波束增益，其中的元素可以表示为：

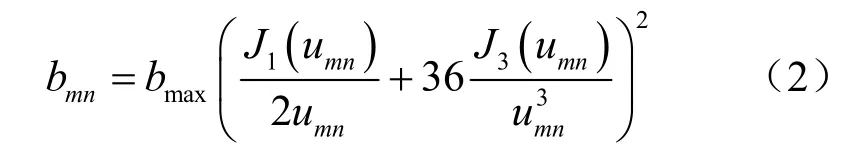
其中，bmax表示卫星天线的最大增益，J1(·)和J3(·)分别是1阶和3阶的第一类贝塞尔函数，并且umn=2.07123sinφmn/sinφ32B，φmn表示第m个用户相对于第n个波束的偏轴角，φ32B为单侧半功率波束宽度。Cm表示自由空间损耗，可表示为：

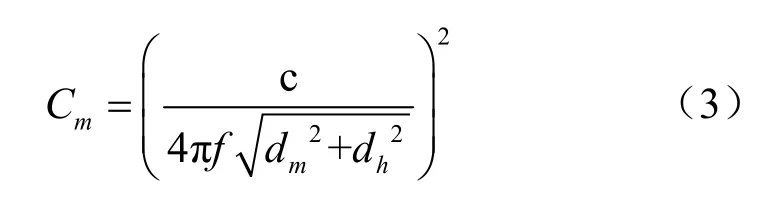
其中，c为光速，f是载频频率，dh≈35786 km表示卫星高度，dm是第m个用户到卫星覆盖区域中心距离。

此外，式（1）中，Gr表示接收天线增益。当系统工作在Ku及以上频段时，通常采用抛物面天线，其表达式为：

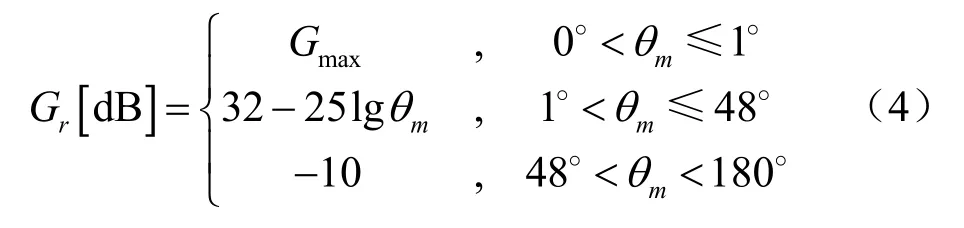
其中，Gmax为抛物面天线轴向的最大增益，mθ为第m个地球站相对于卫星的离轴角。

在对无人机—用户信道建模时，除了考虑无线信道的衰落特性，还要考虑无人机波束增益、电波传播损耗等实际参数的影响。于是，信道可以建模为：

其中，h∈ CN×1表示无人机—用户链路的信道响应矢量，g表示链路的小尺度衰落，L是信道系数，其综合考虑了无人机发射天线增益，用户接收天线增益，自由空间路径损耗以及噪声的影响，可得式（6）：

其中，c、f和d1分别表示光速、无人机信号传输频率以及无人机到用户的距离。

此外，式（5）中的g表示链路的小尺度衰落，可以建模为：

其中，ρ服从莱斯分布，a(θ)∈ CN×1为相控阵导向矢量，取决于期望用户的所在方向，可由式(8)表示：

其中，θ为信号到达角，d2为天线阵源间距，λ为载波波长，N为天线数。

与此同时，基站下行链路服从瑞利衰落，可以建模为[19]：

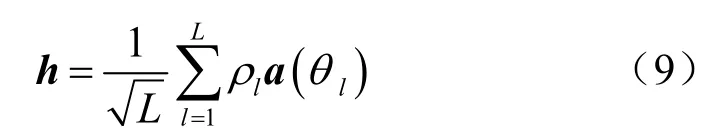
其中，L为多径数，lρ为瑞利衰落系数，lθ为第l个多径分量到达方向，且在区间上服从均匀分布，Δθ为角度拓展。

2.2 信号模型

根据图1的系统模型，信号的传输可以分为两个阶段，在第一阶段中，卫星采用点波束技术发送信号至无人机中继。假设卫星发送信号为同时无人机中继收到卫星信号的K个同频干扰信号xk,k={1 , 2,… ,K}，满足因此，无人机中继接收到的信号可以表示为：

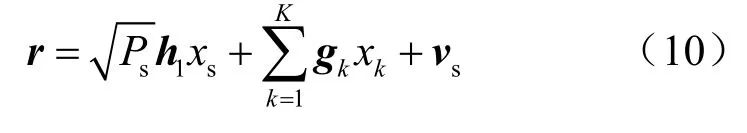
其中，Ps为卫星的发射功率，h1为卫星到无人机中继的信道矢量，gk（k∈ { 1,2,…,K}）表示第k个干扰信号到无人机中继的干扰信道矢量，vs∈CN×1为服从均值为 0、协方差矩阵为的加性高斯白噪声矢量，其中，IN为单位矩阵。

无人机中继采用 BF技术对信号r进行接收，即：

其中，wu∈CN×1表示接收BF权矢量。

在第二阶段，无人机中继采用BF技术将接收到的信号sˆ转发给次级用户，转发后的信号表示为：

其中，w2∈CN×1为发射 BF权矢量。次级用户接收到的信号为：

其中，h2是无人机中继到次级用户的信道矢量，ns为服从均值为0、方差为的加性高斯白噪声。将式（10）～式（12）代入式（13）得：

同一阶段，主用户接收基站发送的信号以及来自无人机中继的干扰信号，假设基站发送信号为且满足，则主用户接收信号为：

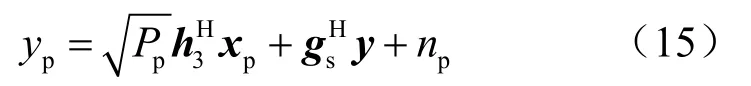
其中，h3表示基站和主用户之间的信道矢量，gs为无人机中继到主用户的干扰链路矢量，np为加性高斯白噪声，其均值为0、方差为。将式（10）～式（12）代入式（15）中，可以得到：

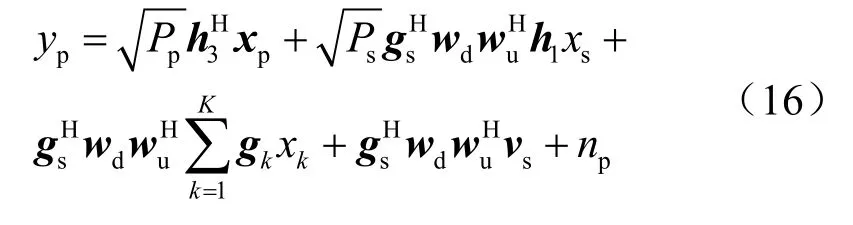
次级用户信干噪比sγ定义为：

其中，Psig、Pint和nP分别表示次级网络的期望信号功率、干扰功率和次级用户端的噪声功率。

利用式（14），次级网络的期望信号功率Psig表示为：

其中，卫星到无人机中继的信道协方差矩阵以及无人机中继到次级用户的信道协方差矩阵分别表示为

同样地，次级用户受到的干扰功率Pint可以表示为：

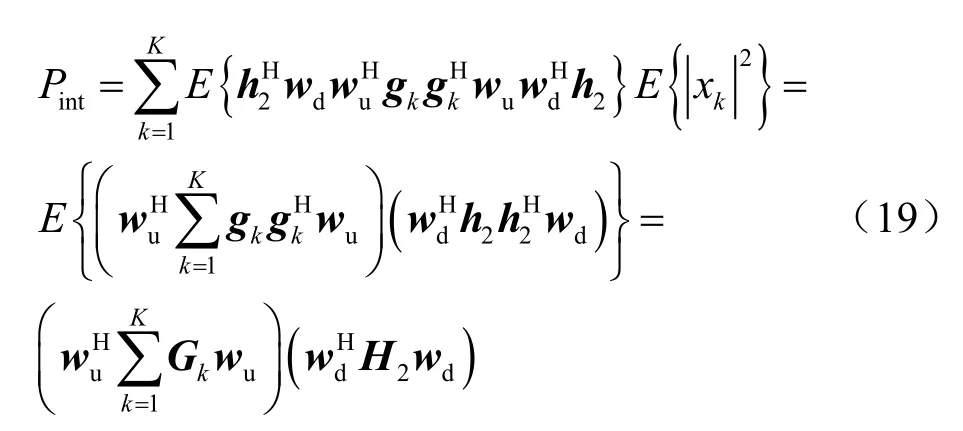
同理，可求得次级网络接收端的噪声功率nP，表示为：

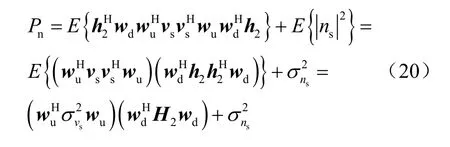
根据式（16），第二阶段中主用户受到的干扰功率为：

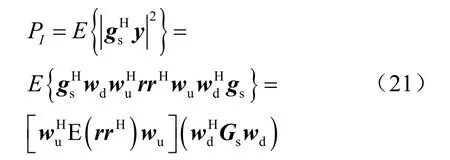
将式（22）代入式（21），可求得第二阶段主用户受到的干扰功率为：

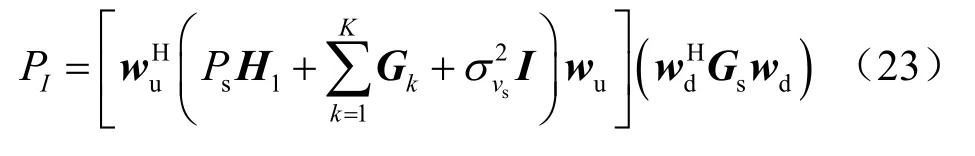
将式（18）、式（19）以及式（20）代入式（17），则次级用户信干噪比表示为：

基于上述建立的系统模型和推导的信号流程，本文将给出两种不同的波束成形算法。

3 基于次级用户信干噪比最大化准则的BF算法

为了保证次级用户接收信号的可靠性，本节考虑次级用户已知统计CSI情况，以无人机中继发射功率受限和主用户干扰功率小于门限值为约束条件，建立以次级用户信干噪比最大化为目标函数的优化问题，该问题在数学上表示为：

其中，PI为主用户受到的干扰功率，Ith是主用户能够容忍的最大干扰功率，为中继站最大发射功率。

将式（24）以及式（23）代入式（25），则优化问题表示为：

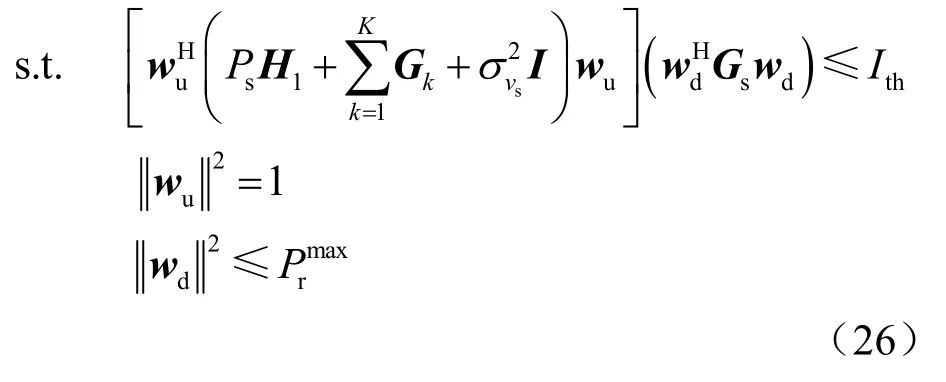
由于上述问题难以直接有效求解，接下来本文结合广义瑞利商，采用迭代算法解决原优化问题，并进一步推导了每一次迭代的闭式最优解。

3.1 基于迭代的BF算法

观察问题（26）可得，接收波束权重wu和发送波束权重w2的求解是相互独立的，不妨将上述优化问题转化为如下两个问题进行求解，其一表示为：

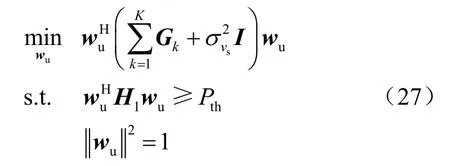
其中，Pth为无人机中继接收到的有用信号功率最小值。其二表示为：

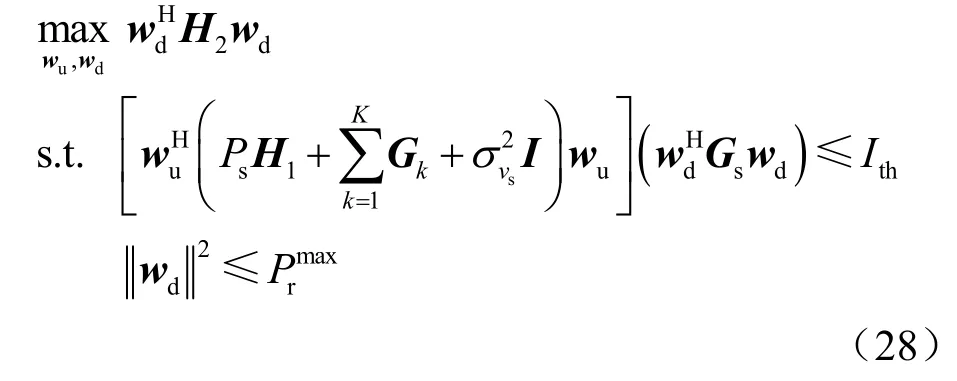
优化问题（27）约束以及优化目标关于wu的单调性具有一致性，因此第一个不等式约束可转化为等式约束，则式（27）可重构为：

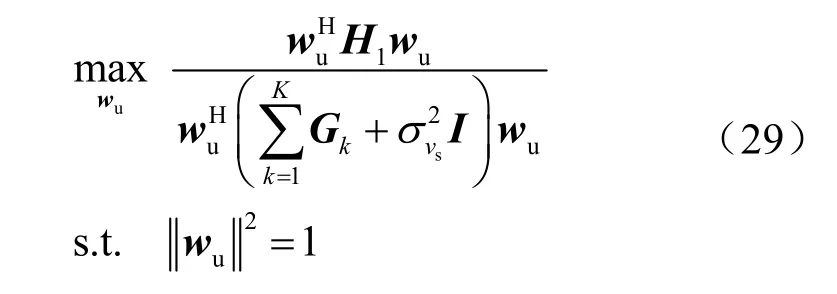
上述问题符合广义瑞利商的求解形式，可求出接收 BF权矢量的最优解为wu=v=表示矩阵最大特征值对应的特征向量。则：

进一步，有：

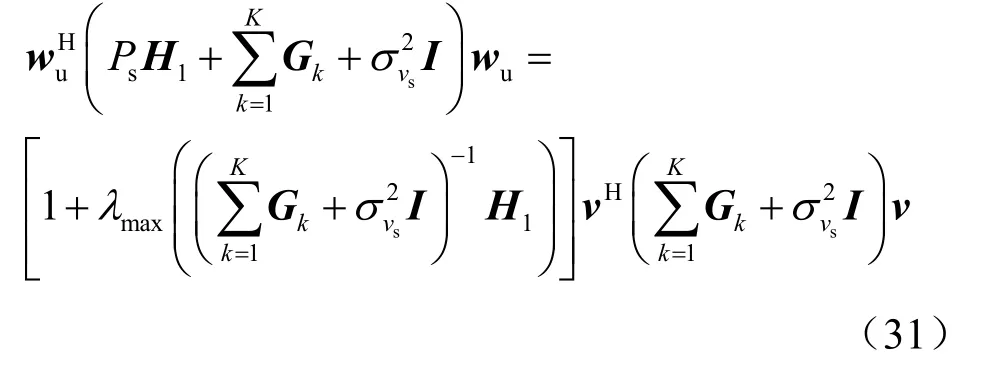
此时，将问题（28）中的优化变量wu看作已知解，则问题（28）可重新构建为：

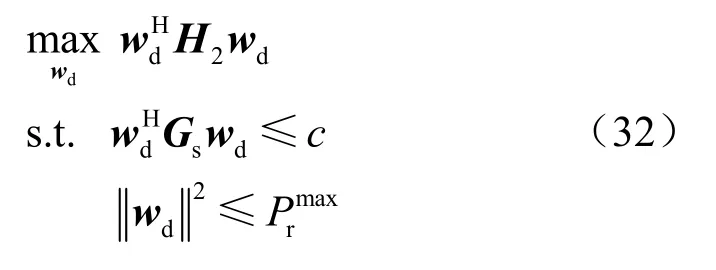
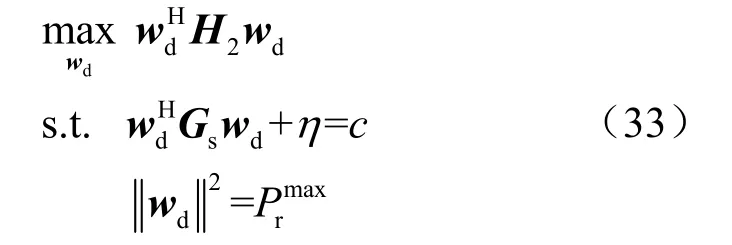
进一步，可将式（33）化简为：

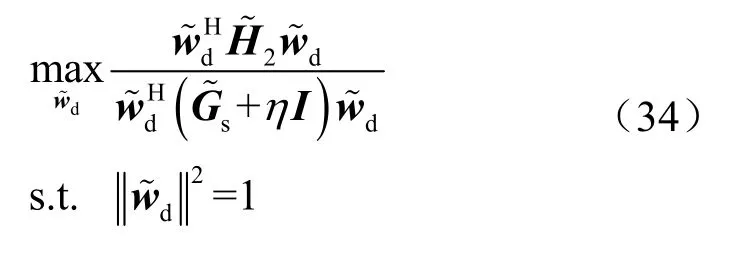
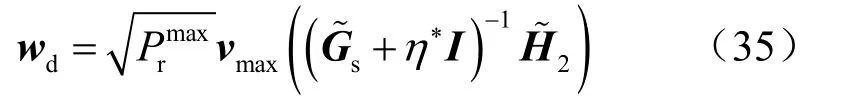
式（35）最优目标值相对于η具有单调性，使用如算法1中所述的二分法搜索，通过求解具有不同η的优化问题（33），从而获得最优值η*。

算法1基于迭代的BF算法

输入干扰功率门限值Ith，中继站发射功率最大值，信道矢量h1、h2、h3，干扰信道矢量gk（1≤k≤K）以及gs；

（1）初始化终止误差ε＞0，U以及L(满足η*∈ [L,U])，迭代次数k=0以及c；

（2）令ηmi2=(U+L)/2；

（3）令η=ηmi2，检查问题（33）可行性：若不可行则令L=ηmi2并执行步骤（5），可行则根据式（35）求解对应w(k)并执行步骤（4）；

（5）如果U-L≤ε,则终止算法；否则，执行步骤（2）；

输出发射BF成形权矢量w2。

将式（30）以及发射BF权矢量式（35）代入式（24），则最大信干噪比表示为：

上述 BF方案提出结合广义瑞利商和迭代算法的方案，虽然可求解优化问题（26），但是也存在计算复杂度较高的问题，因此本文为了降低计算量，提出了一种具有低复杂度的迫零波束成形方案。

3.2 基于迫零的BF算法

由广义瑞利商可知wu=v，表示矩阵最大特征向量对应特征值。将wu代入原优化问题（26），结合式（30）有：

其中，UA、UB为矩阵H3的特征向量，且UB为UA的正交子空间，Aλ为UA对应的特征值，将w2投影到H3的零空间中，即：

式（38）第二个约束以及优化目标关于wd单调性具有一致性，因此可将不等式约束转化为等式约束，将式（40）代入式（38），则优化问题可转化为：

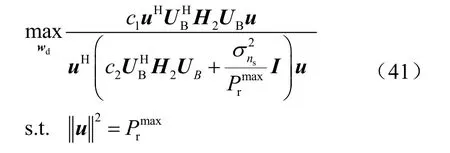
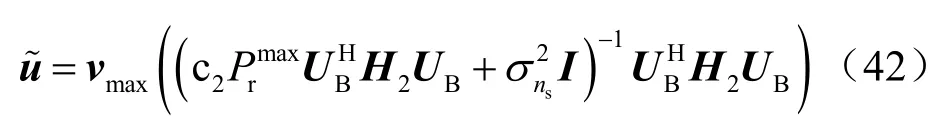
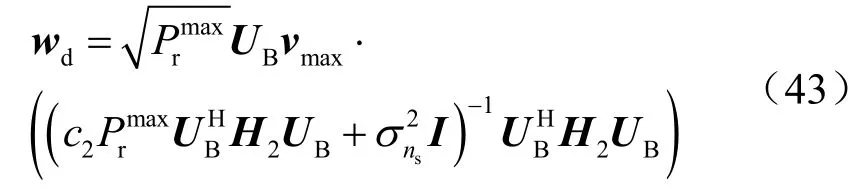
利用式（24）、式（30）以及式（43），次级用户信干噪比可表式为：

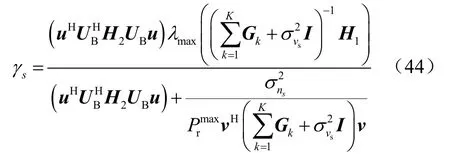
3.3 复杂度分析

本节采用浮点运算理论分析计算复杂度[20]。具体表示为一次浮点运算指的是一次实数浮点运算，即一次实数相加减或者相乘除记为一次浮点运算。除此之外，复数相加减、相乘除则分别包括2次以及6次实数浮点运算。参考文献[21]给出了一些基本运算复杂度：维数分别为mp和pq两复数矩阵相乘需要8mpq次浮点运算；维数为2m共轭矩阵求逆则需要次浮点运算，同样维度的实数矩阵求逆需要次浮点运算，除此之外，同样维度实对称矩阵求逆则需要浮点运算次数为本文针对基于迭代的BF算法，考虑算法1达到收敛需要的迭代次数为τ，则迭代算法需要大约次浮点运算。同理，假设矩阵Gs零特征值个数为K,0＜K＜N，则迫零算法中浮点运算数目大约为

4 仿真与结果分析

本节给出了计算机仿真以验证理论分析结果，不仅定量分析了无人机中继天线数对系统可达速率的影响，并给出了基于迭代算法的BF方案中，干扰功率门限值以及中继最大发射功率对于次级用户信干噪比的影响。在仿真过程中，考虑主用户随机分布在无人机与基站共同覆盖区域，次级用户在无人机覆盖范围内随机分布，其余具体参数设置见表1。

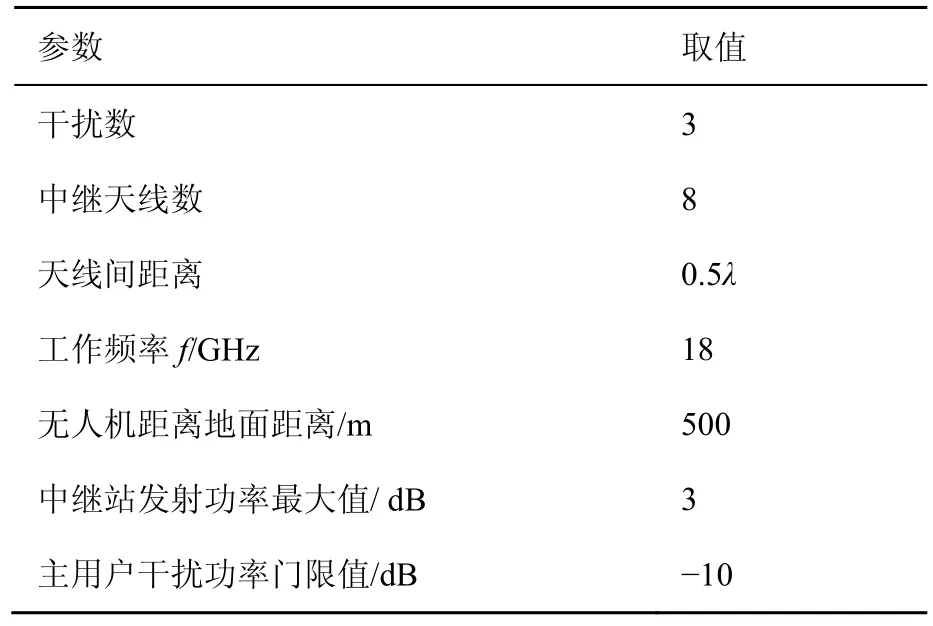
表1 参数设置

图2和图3分别给出了无人机中继接收与发射BF的归一化辐射方向图。考虑卫星发射端在无人机中继水平角10°方向，从图2中可以看出，对于归一化接收BF方向图，卫星位置位于接收主瓣方向，干扰均在零陷位置，说明本文所提方案在保证准确接收信号质量的同时，能够有效抑制干扰信号。此外在图3中，相对于最大比传输（maximum ratio transmission，MRT）方案，本文所提迭代算法以及 ZF方案均能使得波束增益最大方向对准次级用户，零陷对准主用户，这说明本文所提出的两种方案能够有效抑制来自其他方向的干扰，从而在一定程度上提高网络的抗干扰性能。

图2 接收波束成形归一化方向图

图3 发射波束成形归一化方向图

图4为迭代、ZF与MRT 3种方案下，次级用户可达速率随天线数的变化直方图，其中无人机中继站天线数N={8,12,16,32}。由图4可知，每种方案下，可达速率均随着天线数增加而提高，这是因为多天线技术的阵列增益可提升通信质量，故可以通过增加天线数提高系统的可达速率；同样，当天线数相同时，迭代算法系统可达速率要高于ZF方案和MRT方案的可达速率，验证了本文所提的迭代算法相较于ZF方案和MRT方案更能有效提升系统性能，这是因为MRT算法仅考虑次级用户接收信号功率最大而不考虑干扰方向。与此同时，天线数增加，ZF算法提升系统性能更为明显，这是因为天线数增加，自由度增加，因此ZF实现算法效果接近于迭代算法。

图4 3种方案下可达速率直方图

图5给出了所提基于迭代算法的BF方案中干扰功率门限值和中继发射功率对信干噪比的影响。从图5中可以看出，随着干扰功率门限值的增加，次级用户的信干噪比也随之增长，当干扰门限值增加到一定值，次级用户的最大信干噪比增长速度变慢；与此同时最大发射功率的增长也会增加次级用户的最大信干噪比，可以通过适当增加干扰门限以及最大发射功率值提高次级用户的最大信干噪比。

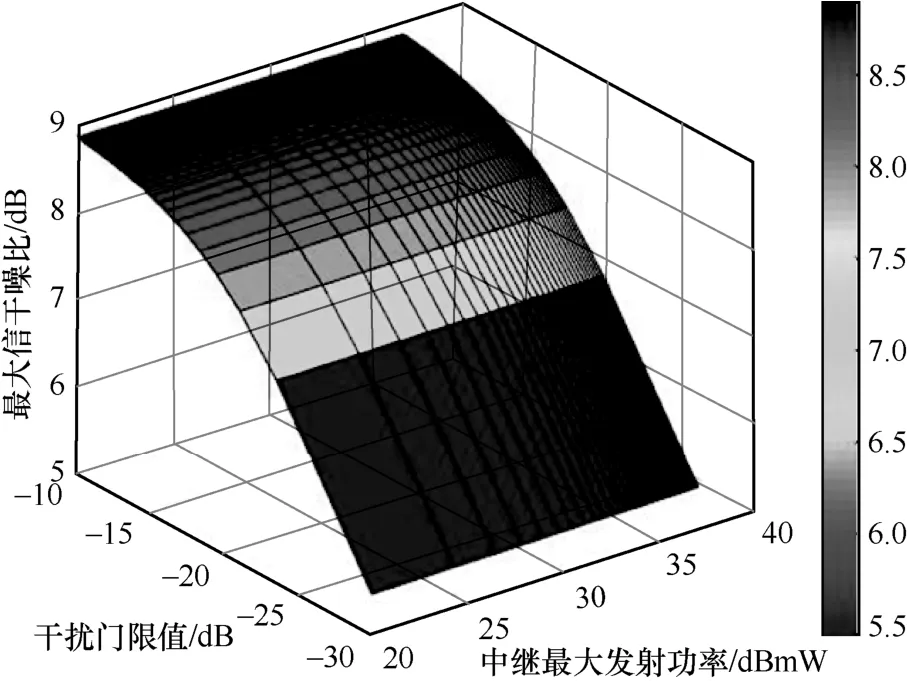
图5 信干噪比与干扰门限和发射功率的关系

5 结束语

本文研究了基于无人机中继的星地认知网络的信息传输问题。考虑基于无人机中继的卫星网络作为次级网络，地面网络作为主网络。首先推导出次级用户信干噪比表达式，在此基础上，针对无人机中继发射功率受限和主用户干扰功率受到限制的情况，构建了次级用户信干噪比最大化问题。接着分别提出了基于迭代以及基于迫零的两种BF方案，并推导求得BF权矢量的解析表达式和闭式解。最后，仿真结果表明所提两种波束成形方案能够有效地抑制干扰，提升了通信系统的抗干扰能力。